IP3调控星形胶质细胞自发性钙振荡的动力学分析

崔荣涛，刘苏雨，孙伟刚

(杭州电子科技大学理学院，浙江 杭州 310018)

0 引 言

星形胶质细胞被认为是大脑中大量神经胶质细胞中的一种亚群，其表征的钙振荡活动与大脑认知学习和记忆有关。钙振荡模式是星形胶质细胞的一种基本信息编码方式[1]，通过其钙信号的传导，促进了神经元网络的信息编码和钙振荡传播等活动[2]，自发性和诱导性钙振荡就是其向细胞周围环境输出信息的媒介。而这其中的自发性钙振荡与细胞谷氨酸依赖性的钙波类似，也能促使细胞通过释放谷氨酸对神经元产生作用[3]，其背后形成的电生理机制尚未研究清楚。

动力学建模仿真可用于解释神经电生理实验中诸多现象。在分析研究星形胶质细胞自发性钙振荡模式方面，建立了很多数学物理模型[4-8]。例如，基于Li-Rinzel模型[4]和Höfer模型[5]，Riera等[7]提出了一种描述星形胶质细胞中自发的钙离子振荡机制的模型，研究结果表明，电容性钙内流对模型自发性钙振荡产生的作用微乎其微，而1,4,5-三磷酸肌糖(IP3)对其的作用显著，当IP3的浓度增长至一定范围内，且星形胶质细胞内Ca2+浓度超过其基线水平，系统表现出周期性钙振荡模式。Denizot等[8]建立了生理上更为真实的星形胶质细胞动力学平均场模型，研究发现，星形胶质细胞自发性钙振荡模式及其频率受内质网上IP3受体(IP3R)通道空间支配的调控，同时应用真实的星形胶质细胞内钙机制和参数调配，再现了共聚焦显微镜下钙微区域测量的自发性钙信号。星形胶质细胞内IP3浓度对自发性钙振荡的影响至关重要，细胞内IP3生产量和降解率是决定其含量的重要指标[9-12]。本文在已有模型研究的基础上，构建一类简化的星形胶质细胞动力学模型，考察星形胶质细胞内IP3生产量和降解率对细胞自发性钙振荡模式影响的动力学调控机制。

1 模型描述

为分析星形胶质细胞不受外界影响而产生自发性钙振荡的行为机制，本文假定对一封闭的星形胶质细胞进行研究。星形胶质细胞中钙离子处理过程如图1所示。模型中包含星形胶质细胞钙离子浓度变化的几种关键的动力学机制：内质网(ER)上主要释放钙离子的IP3受体通道、Ca2+内流到内质网的钙泵通道、IP3参与的PLCδ酶转化、钙离子泄漏通道以及细胞内自主生产和降解IP3的附属结构。其中，细胞体积和细胞内内质网的体积结构比为γ，假定细胞质内钙离子浓度c和内质网上钙离子浓度cER关系满足常数c0=c+γcER，借助Riera模型[7]和Handy[9]模型，本文提出的刻画星形胶质细胞自发性钙离子活动机制的动力学模型描述如下：

图1 星形胶质细胞中钙离子处理过程

(1)

(2)

(3)

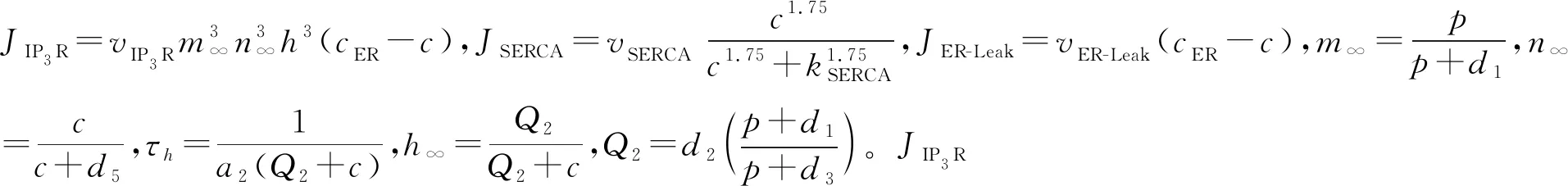
2 数值模拟结果与分析

针对文献[7]在实验中发现的影响星形胶质细胞自发性活动产生的显著性因素，本文聚焦星形胶质细胞内IP3生产量和降解率与星形胶质细胞自发性活动之间的关系，尤其是自发性Ca2+振荡模式，揭示星形胶质细胞基于钙离子自调节活动的动力学机制。本文采用四阶-五阶Runge-Kutta算法进行数值模拟。

2.1 动力学稳态分析

星形胶质细胞内IP3生产量XIP3和降解率kIP3在不同浓度情况下，星形胶质细胞模型呈现的稳态动力学行为如图2所示。首先，依据Ca2+浓度的相对大小，把系统的平衡态分为低平衡态和高平衡态，[Ca2+]≤0.20 μΜ表示低平衡态，[Ca2+]>0.20 μΜ表示高平衡态。在图2(a)中，XIP3和kIP3取值较小，系统达到了一个低平衡态。当XIP3增加到0.80时，系统呈现出周期性振荡，且星形胶质细胞内表现出幅值约为0.5的自发性钙离子振荡状态，如图2(b)所示。此时细胞内IP3浓度达到高值的稳定状态，IP3R通道未被钙离子激活的机率降低。在此基础上，增大IP3的降解速率至0.50，系统仍呈现出周期性振荡状态，如图2(c)所示，但自发性钙离子振荡的频率显著降低，胞内IP3浓度显著降低。进一步控制胞内IP3生产量，继续提高IP3的降解率至0.80，系统的钙活动最终由周期性振荡转变为低平衡态，如图2(d)所示，但IP3生产量降低使得IP3R通道未被钙离子激活的机率提高。由此可以看出，系统受IP3生产量XIP3和降解率kIP3的影响显著，并呈现出平衡稳态和周期性振荡之间的相互转迁行为。假使星形胶质细胞内IP3处于高产状态，系统最终又回到了周期性振荡状态，如图2(e)所示。持续高浓度的IP3促进了内质网上大量的钙释放，进而高浓度的钙又抑制了IP3R通道开放释放钙离子，所以，相对于图2中的(b)和(c)，自发性钙振荡模式的频率有所降低。在细胞处于IP3高产的情况下，进一步降低IP3降解率至0.15，使得胞内的IP3浓度处于高饱和状态，此时系统又回到高平衡状态，如图2(f)所示，并且IP3R通道开放机率降低，细胞质内的钙离子浓度降低。

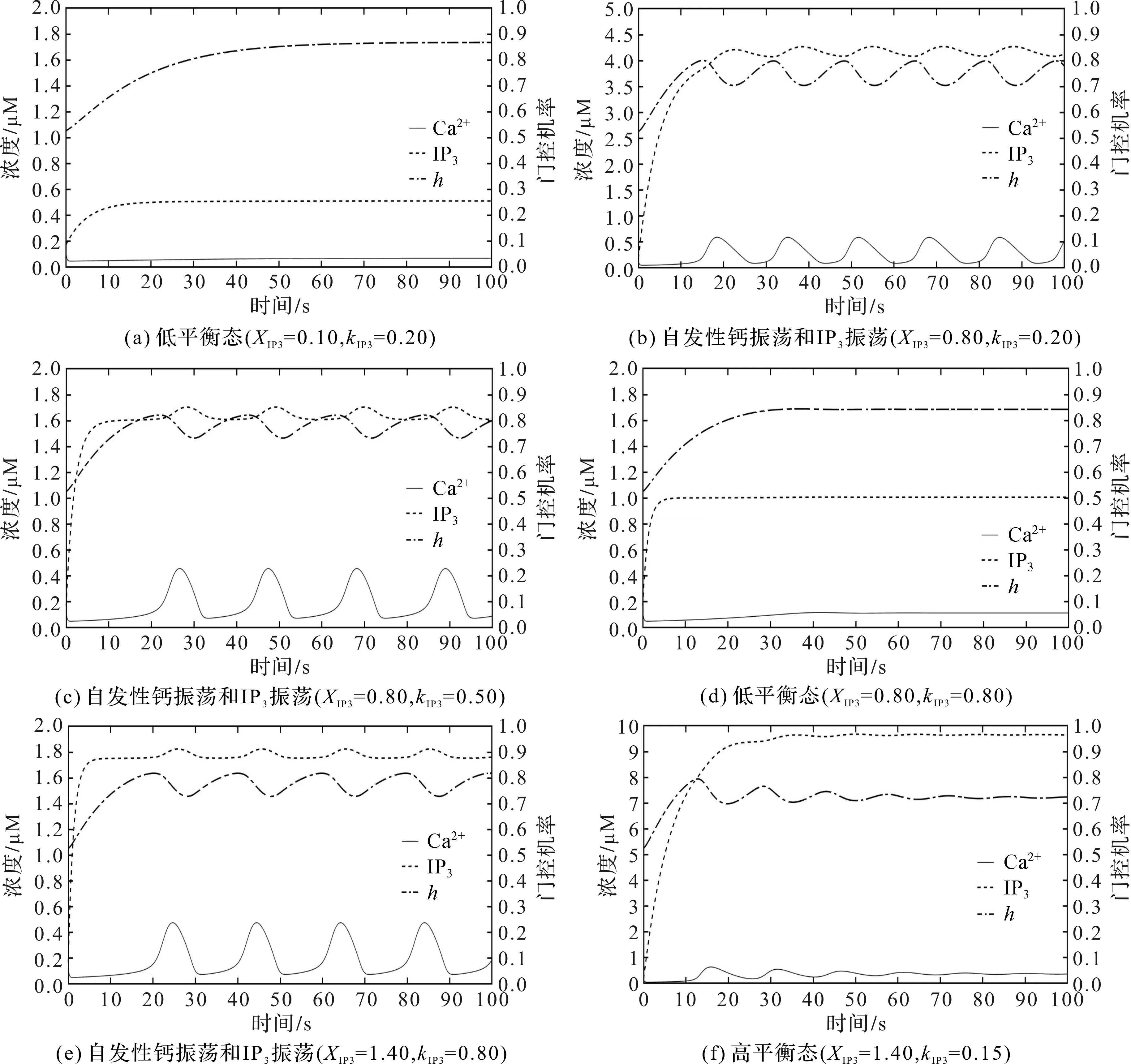
图2 星形胶质细胞模型随参数XIP3和kIP3变化的自发性活动时间序列图

2.2 动力学分岔分析

从分岔动力学角度分析IP3生产量XIP3和降解率kIP3的变化，诱导系统呈现出平衡态与振荡状态之间的转迁行为，星形胶质细胞模型的动力学分岔如图3所示。图3(a)描述系统受分岔参数XIP3∈[0,2.00]影响下呈现的分岔行为。XIP3∈[0,0.21)时，系统最终处于稳定平衡状态；XIP3=0.21时，分岔点HB1处，系统发生超临界Hopf分岔，稳定平衡点失稳并分岔出稳定极限环，模型呈现由低平衡态到自发性钙振荡模式的转迁。随着XIP3进一步增大，XIP3=1.13时，HB2点处，系统发生亚临界Hopf分岔，不稳定平衡点变得稳定且分岔出不稳定的极限环。XIP3持续增大至1.33，LP点处，系统发生极限环鞍结分岔，稳定极限环与不稳定极限环相遇并湮灭。XIP3∈(1.13,1.33)时，系统表现为稳定极限环和高平衡点稳态行为。当系统的初始状态处于这两种稳态下的任何一方吸引域内，系统最终均会稳定到这种状态，因此可通过施加外部刺激改变XIP3的量，从而使系统在这2种稳态行为之间相互跳跃。当XIP3∈(1.33,2.00]时，系统最终达到高平衡状态。

图3 星形胶质细胞模型的动力学分岔图

在选定区域为XIP3×kIP3∈[0,2]×[0,1]时，XIP3和kIP3变化下，系统表现的动力学分岔行为如图3(b)所示。从XIP3增大的方向看，在区域I内，系统表现为低平衡态；随着XIP3的增大，系统经过超临界Hopf分岔行为(实线)进入楔形区域II，系统表现为稳定的极限环，有自发性钙振荡行为。进一步增大XIP3和减小kIP3，系统由楔形区域II经过亚临界Hopf分岔(点线)进入楔形区域III，系统依然保持稳定的极限环，并且还有另一个稳定平衡态(高平衡态)，系统处于双稳态行为。再从kIP3减小方向看，继续降低kIP3，系统由双稳态区域III经过极限环鞍结分岔LP(“+”线)进入三角区域IV，表现为稳定的高平衡态。从动力学控制角度来说，为求得使系统呈现特定时间域内广泛的自发性钙振荡模式，可诱导星形胶质细胞IP3生产量和降解率处于特定区域内，并针对此特定参数，做出一系列控制自发性钙振荡模式的策略。

3 结束语

本文建立了一个封闭的星形胶质细胞动力学模型，主要研究星形胶质细胞内IP3生产量和降解率对细胞自发性钙振荡的影响及其平衡状态的动力学机制。通过数值模拟发现，系统呈现出Hopf分岔(超临界和亚临界)和极限环鞍结点分岔行为，再现了自发性钙信号现象，表明生物学上星形胶质细胞自发性钙振荡模式及其频率受自身IP3生产率和降解率的显著调控。对于大多数的星形胶质细胞系统而言，时滞是普遍存在的，而本文的星形胶质细胞钙动力学模型并未考虑时滞，因此带有时滞的星形胶质细胞钙动力学模型是今后研究的突破口。