基于时间方法的电压源逆变器死区补偿研究

闫 博，王家军

(杭州电子科技大学自动化学院，浙江 杭州 310018)

0 引 言

空间矢量脉宽调制(Space Vector Pulse Width Modulation，SVPWM)技术具有开关损耗小、便于数字化等优点，广泛应用于变频逆变和交流调速等领域[1]。SVPWM控制的三相电压源逆变器为180°导通方式，每次换流都在同一相上下桥臂间进行。为了避免换流过程中上下桥臂发生直通，需要在功率开关管的控制信号中增加一段死区时间，这样虽然保证了逆变器的安全，但是导致逆变器输出电压基波幅值降低，输出电流引入低次谐波[2]。

针对电压源逆变器(Voltage Source Inverter，VSI)死区效应问题，提出了不同的控制方法，大致分为两类，即无死区控制方法和死区补偿控制方法。无死区控制方法可以避免在同一相上下桥臂间发生换流，使同一相上下桥臂间不再出现直通短路的现象[3-4]。因此，无需再设置死区时间，但输出的电压和电流波形仍存在明显畸变。死区补偿控制方法包括平均电压补偿法、脉冲电压补偿法和观测器法。文献[5]提出一种基于平均误差理论的补偿方法，根据电流极性将死区效应造成的电压误差补偿到指令电压中。该方法控制简单，但补偿精度较低。文献[6]提出一种新型的脉冲电压补偿法，根据电流极性和死区时间，提前或延后开关管的导通关断时间。该方法补偿精度较高，但需要实时对控制信号的脉宽进行调整，占用较大的计算资源。文献[7-8]提出的观测器法将死区效应引起的电压误差作为扰动量，观测器对其进行在线观测和补偿。该方法不依赖电流极性的检测，但其作用效果很大程度上取决于PI控制器参数的整定，因此不易调节。针对上述方法的不足，本文提出一种基于时间的死区补偿方法，分别推导出理想和实际条件下矢量作用时间的表达式，将计算出的时间误差作为补偿量，在SVPWM算法矢量作用时间的基础上，通过增加补偿量实现死区的补偿。

1 死区效应对输出电压的影响

1.1 三相参考电压的划分

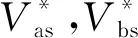
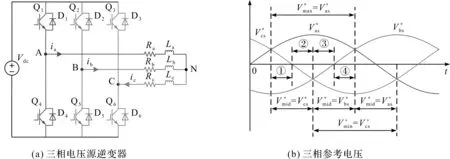
图1 三相逆变器结构和参考电压

1.2 SVPWM算法原理

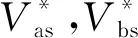
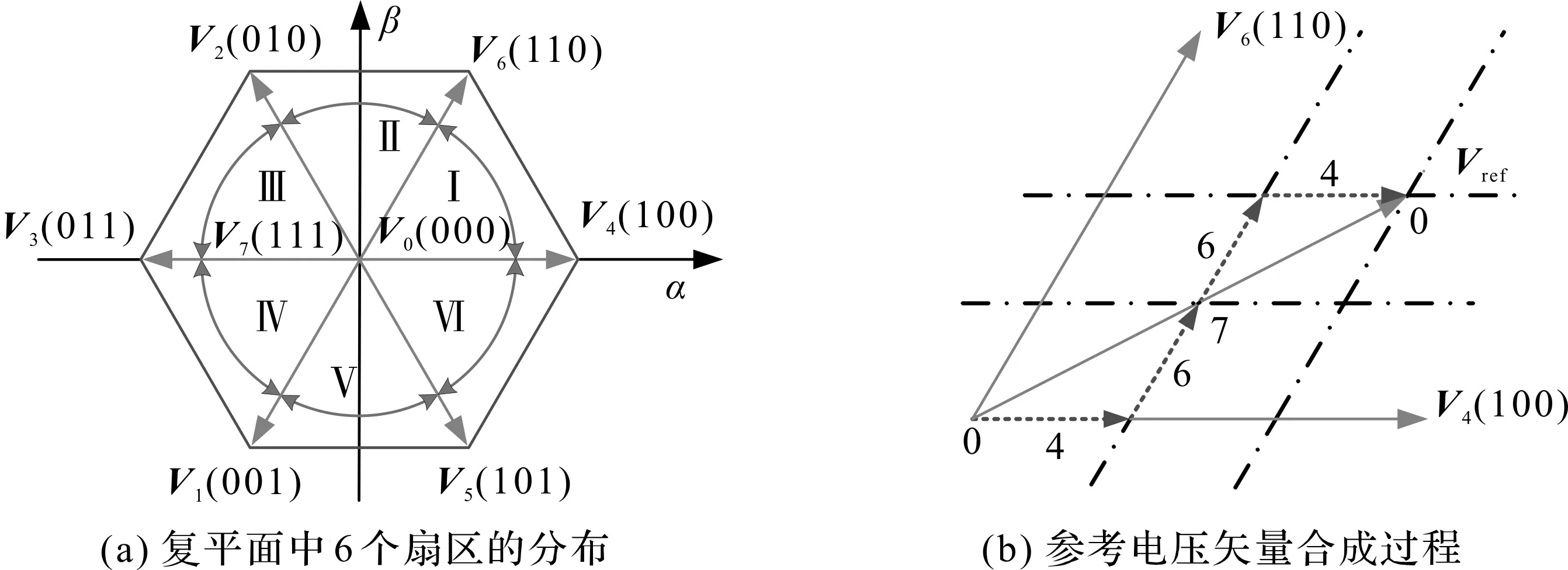
图2 复平面的扇区分布和扇区内的矢量合成过程

1.3 电压误差分析

在理想情况和实际情况下，根据开关信号SA，SB和SC分别得到第1扇区内的三相电压波形如图3所示，其中T1，T2和T0分别表示SVPWM算法中有效矢量和零矢量的作用时间。本文选择七段式SVPWM算法，为减少输出电压的谐波，并使其具有对称性，将各基本电压矢量的作用时间平分为2份，同时对称地分布在1个开关周期Ts内。

理想情况下不考虑死区时间，不计功率管自身的压降损耗，并假设其开通和关断可以在瞬间完成，该条件下的三相电压波形如图3(a)所示，由电压矢量的作用时间和直流母线电压共同确定：

(1)

式中，Vmax，Vmid和Vmin分别为各相的平均输出电压。T1，T2和T0分别为有效矢量和零矢量的作用时间。将式(1)中的平均输出电压替换为参考电压，推导出产生各相参考电压的作用时间：

(2)

T0(T7)=Ts-T1-T2

(3)

功率器件实际工作时会产生压降损耗，并且其开通和关断均存在延时，将这些特性统称为逆变器的非线性特性。包含非线性特性和死区时间的实际相电压，如图3(b)所示。在1个开关周期内相电压波形具有对称性，因此仅分析半个周期Ts/2的相电压即可。从图3(b)可以看出，电压误差主要由时间误差和压降损耗组成。图中条形斜线区域表示的压降损耗由功率器件自身特性和流过它的电流共同决定，而时间误差由逆变器死区时间Td，功率器件的开通延时ton和关断延时toff共同决定。

图3 逆变器三相输出电压波形图

根据图3(b)的电压波形和图4的等效电路可以得到各电压矢量的实际作用时间和各相的输出相电压。在t0-t3期间实际的矢量作用时间、中性点电压和各相的平均输出相电压分别为：

TS0/2=(T0/2)+(Td/2)+ton

(4)

(5)

式中，VN为中性点电压，Vmax(x)，Vmid(x)和Vmin(x)(x=0，1，2，7)分别为不同阶段的最大，中等和最小输出电压，VP(|ix|)和VD(|ix|)(ix=imax，imid，imin)分别为功率开关管和续流二极管上的压降损耗。

在t3-t6期间实际的矢量作用时间、中性点电压和各相的平均输出相电压分别为：

TS1/2=(T1/2)-(Td/2)-ton+(Td/2)+ton=(T1/2)

(6)

(7)

在t6-t8期间实际的矢量作用时间、中性点电压和各相的平均输出相电压分别为：

TS2/2=(T2/2)-(Td/2)-ton-(Td/2)+toff

(8)

(9)

在t6-t8期间实际的矢量作用时间、中性点电压和各相的平均输出相电压分别为：

TS7/2=(T7/2)+(Td/2)-toff

(10)

(11)

当中等参考电压的电流极性为负时，采用同样的分析方法画出对应的等效电路，由等效电路推导出各个时间段内平均输出电压和电压矢量作用时间的表达式。

图4 各矢量作用时间内的等效电路

1.4 电流极性的检测

图在零点附近的放大波形及其电流极性

2 死区补偿算法

2.1 实际矢量作用时间表达式的推导

功率器件压降的非线性使得由此产生的电压误差很难进行补偿，但该电压误差远小于输出电压。此外，输出电压误差主要取决于死区时间。所以，本文将功率器件上的压降假设为恒定值：

Vsat≈VP(|ix|)≈VD(|ix|)

(12)

虽然Vsat与VP(|ix|)和VD(|ix|)的值并不相等，但实际电压降与恒定补偿值Vsat之间的误差很小。因此，采用简单的恒压降Vsat补偿方法是有效的。

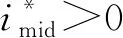
(13)

(14)

(15)

T0(T7)=Ts-T1-T2

(16)

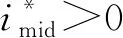
2.2 死区补偿方法流程

本文提出的SVPWM逆变器的死区补偿方法主要包括以下4个步骤：

(4)由最大、中等、最小参考电压和直流母线电压，以及中等电压的相电流极性共同推导出有效矢量和零矢量作用时间的表达式，其中还包括功率器件压降Vsat、开通延时ton、关断延时toff和死区时间Td，这些量均为常值，其大小取决于逆变器自身的硬件特性。

3 仿真结果与分析

3.1 系统仿真参数设置

为了验证本文所提出的死区补偿方法的有效性，分别在死区补偿前后对SVPWM算法控制的电压源逆变器进行仿真实验，实验系统的仿真参数如表1所示。

表1 仿真参数

3.2 结果分析

在三相阻感负载Rx和Lx(x=a，b，c)为2 Ω和0.02 H的条件下，分别对系统在死区补偿前后进行仿真实验，结果如图6所示。由于逆变器输出的三相电流和电压具有对称性，本文均以A相为例。

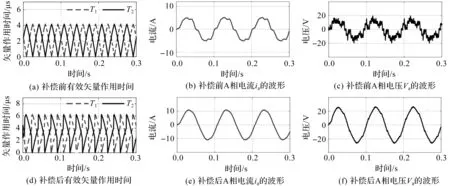
图6 原负载条件下死区补偿前后的仿真结果对比

对比图6(a)和(d)可知，由于本文提出的补偿方法考虑了非线性因素的影响，补偿后的有效电压矢量作用时间T1和T2的值更大。对比图6的(b)，(e)和(c)，(f)可知，补偿前逆变器的输出电流和电压波形正弦度较差，死区效应导致各自的幅值均被削减。在补偿后，ia和Va的波形更加光滑，ia的零电流钳位现象得到了明显改善，同时因死区效应而被削减的相电流和相电压幅值也得到了补偿。

在三相阻感负载增加50%的条件下，对死区补偿前后的系统再次进行仿真实验，结果如图7所示。

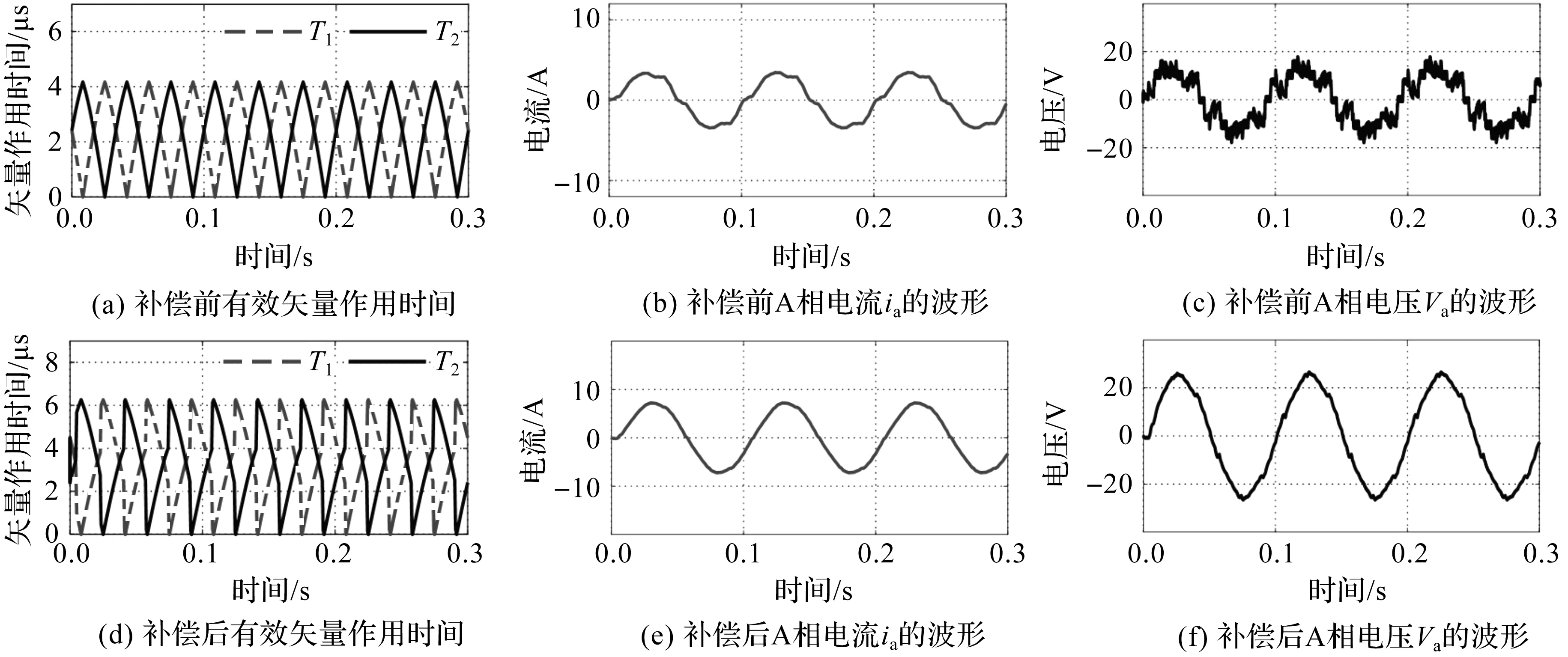
图7 变负载条件下死区补偿前后的仿真结果对比

由图7的(a)和(d)可知，虽然负载大小发生了变化，但矢量作用时间的值仍然不变，说明本文提出的补偿方法与逆变器所带负载的物理模型无关，只与死区时间和逆变器硬件特性有关。对比图7的(b)，(e)和(c)，(f)可知，在负载改变的情况下，本文所提出的补偿方法依然能够有效改善死区效应导致的相电流零点钳位和相电压畸变等不利影响。

为了进一步验证本文提出的死区补偿方法的有效性，分别在原负载和变负载的条件下对死区补偿前后的ia进行傅里叶变换分析，结果如图8所示。

图8 原负载和变负载条件下死区补偿前后的电流谐波分析对比

对比图8的(a)，(c)和(b)，(d)可知，原负载条件下死区补偿前后ia的5次和7次谐波幅值分别从基波幅值的9.47%和5.67%下降为基波幅值的2.02%和0.35%，ia的总谐波失真率从11.19%下降2.23%，变负载条件下死区补偿前后ia的5次和7次谐波幅值分别从基波幅值的8.45%和4.89%下降为基波幅值的1.92%和0.47%。ia的总谐波失真率从9.88%下降为2.20%。因此，本文提出的补偿方法在变负载的情况下，依然能够有效削减相电流低次谐波的幅值，并降低其对基波的影响。

4 结束语

针对逆变器的死区效应问题，本文提出一种基于时间的死区补偿方法，由最大、中等、最小参考电压和中等参考电压的电流极性得到实际电压矢量的作用时间，同时可将其直接提供给逆变器。在整个计算过程中，除死区时间外，还包括功率管压降等非线性因素。虽然提出的补偿方法由电流极性决定，但补偿原理和计算过程较简单，且作用效果显著，具有一定的应用潜力。下一步将本文提出的补偿方法在伺服电机控制系统中进行验证，并根据实验结果不断改进，使其更具实用性。