基于ISSEWD和SOWN的轴承工况识别研究*

戚 航,郑迎华,陈锡渠

(1.新乡职业技术学院 汽车技术学院,河南 新乡 453000;2.河南科技学院 继续教育学院,河南 新乡 453000)

0 引 言

滚动轴承是旋转机械的重要部件,对于保证旋转机械整机的安全运行,具有重要意义[1-3]。许多旋转机械的故障是由轴承故障造成,因此,轴承的故障诊断对于保障企业安全生产具有重大的意义。然而,实际采集到的轴承振动信号极易受环境噪声干扰,非线性和非平稳性较强[4]。

传统的基于“人工特征提取-工况模式识别”的方法[5-7]依赖于繁琐的人工特征提取及选择过程,受主观影响较大。然而,变分自编码器(variational auto-encoders,VAE)[8]是一种生成模型,相比于自动编码器和限制,玻尔兹曼机更适合处理大量的滚动轴承振动数据,VAE能从轴承振动数据中自动学习,有助于判别轴承工况的特征,因此,VAE在机械工况识别领域取得了一定的突破。王昱等[9]利用VAE和齿轮箱振动信号频谱,实现了对齿轮箱各工况的高精度识别;金棋等[10]利用深层VAE学习原始轴承故障样本的概率分布,并利用生成对抗网络训练生成器和判别器网络的参数,最后实现了对轴承智能工况的识别。但VAE训练困难,学习到的网络隐层特征比较模糊,难以体现真实滚动轴承振动数据分布的多样性。

此外,众多研究[11-13]表明:振动信号噪声的存在会严重降低模型的工况识别准确率,经验模态分解[14]4-5及其变体[15]等模态分解降噪方法缺乏严格的理论基础;VMD[16，17]的分解模态个数难以确定;经验小波分解(empirical wavelet decomposition,EWD)[18]结果较稳定,但有效频谱边界难以有效划分。

本文针对EWD和VAE的缺陷,提出一种基于改进谱分割经验小波分解(ISSEWD)和自组织Wasserstein网络(SOWN)的滚动轴承工况识别方法,并通过实验结果证明该方法是否具有工况识别效果。

1 改进谱分割经验小波分解

采用EWD对滚动轴承振动信号的频谱边界进行检测和分割,利用小波滤波器提取相应频段的调幅-调频成分时,由于现场采集到的滚动轴承振动信号会受到大量环境噪声的影响,环境噪声在时域上的幅值较大,功率谱在整个频域内呈现均匀分布,进而淹没了信号中包含的工况特征,降低了工况识别准确率。

考虑滚动轴承振动信号整体频谱均受到环境噪声干扰,若直接分析振动信号的频谱,则得到的极值个数多,不利于后续分析。因此,本文提出一种四分位法检测信号频率谱边界。该方法将数据由小到大分为4等分,3个分割点位置的数值分别记为q1、q2、q3,q3与q1,之差即为四分位距Q,根据Q可设置数据上限;在上限之外的数据记为频谱边界值。

上限计算式如下:

Up=q3+k(q3-q1)

(1)

根据文献[14]6所提方法,此处k取值为2,详细步骤如下:

步骤1:对轴承振动信号x进行快速傅里叶变换(FFT)变换,即:

F(s)=FFT(x)

(2)

Mx=|F(si)|(i=1,2,…,l)

(3)

式中:l—信号x维度的一半。

步骤2:检测Mx的局部极大值,并利用三次样条插值方法生成频谱包络线e(s);

步骤3:检测出e(s)的局部极大值,然后根据式(1)检测出频谱边界值。边界值求出后,N个区间段中的每一段都可表示为An=[Mn-1,Mn],由此得到所有的区间边界。设Mn为第n个边界,母小波定义为An上的带通滤波器,因此,可得EWD的细节系数和近似系数,即:

(4)

(5)

因此,f(t)可被分解为:

(6)

(7)

进行分析所要采用的仿真信号如下:

(8)

式中:f1(t)—余弦信号;f2(t)—调幅-调频信号;f3(t)—白噪声。

采用ISSEWD对f(t)进行分解,分解结果如图1所示。

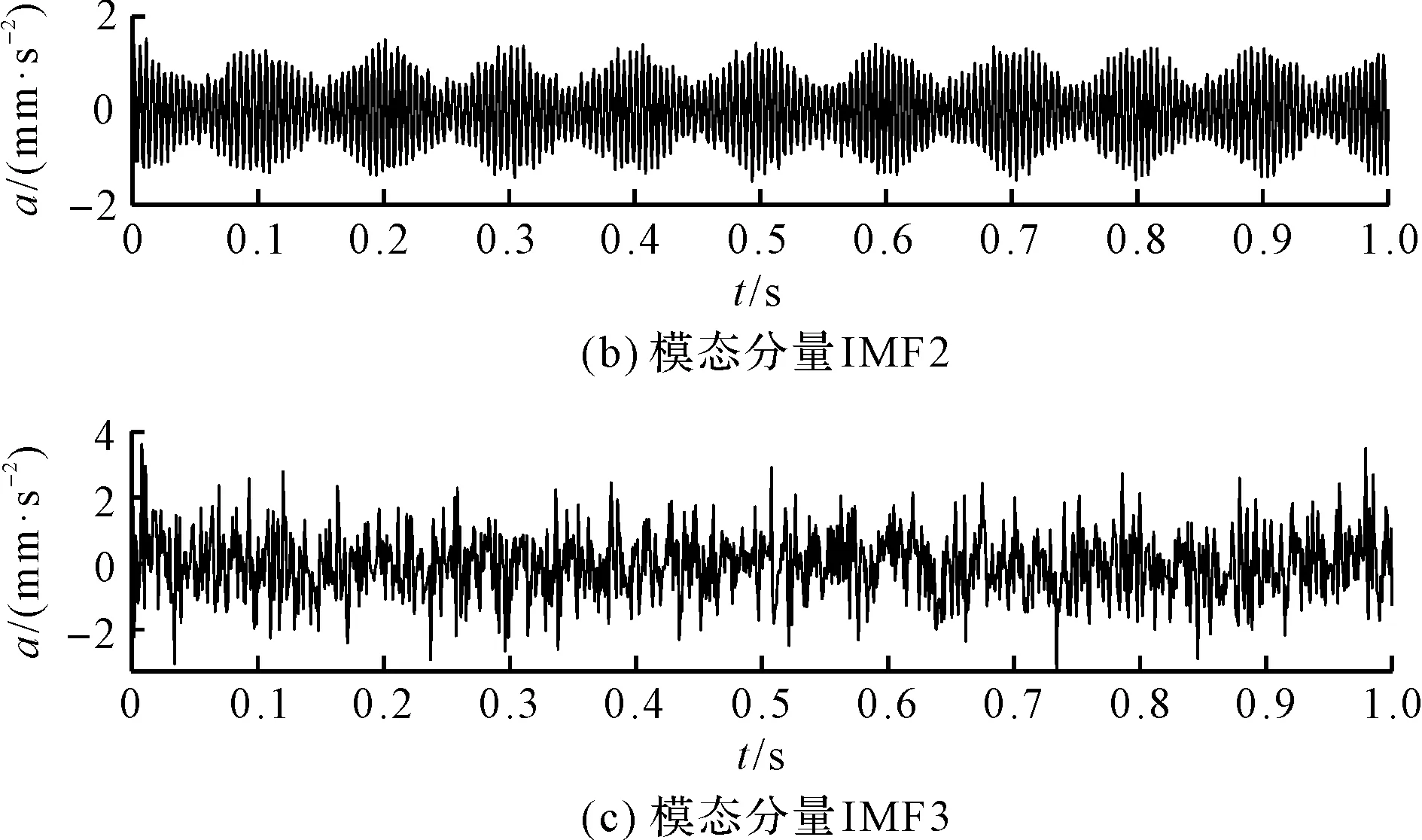
图1 ISSEWD分解结果

由图1可知,ISSEWD能较准确地分解仿真信号,对噪声鲁棒性较强。笔者采用原始EWD对f(t)进行分解,分解结果如图2所示。

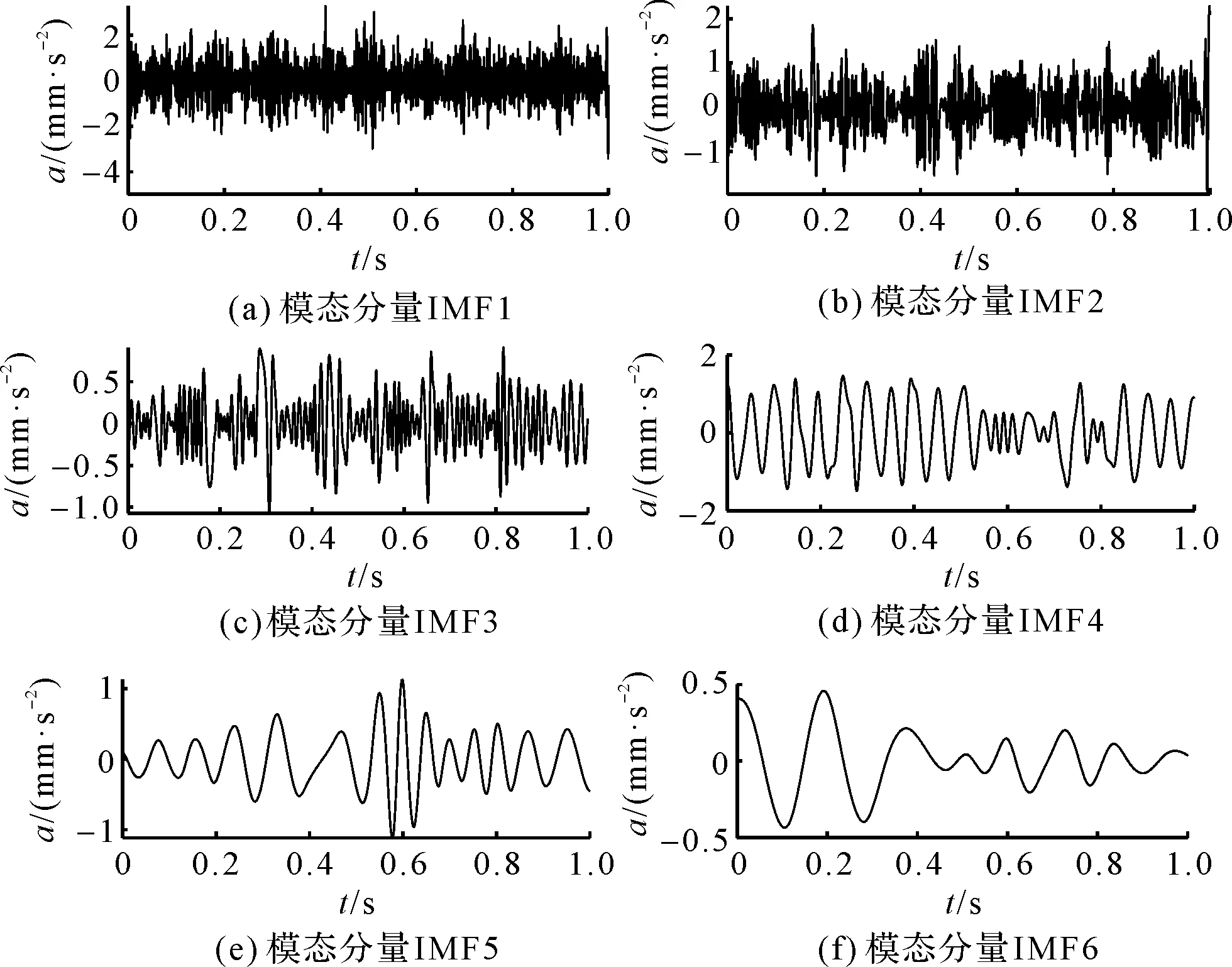
图2 原始EWD分解结果

由图2可知,原始EWD产生了一定的模态混叠效应,频谱杂乱。

2 自组织Wasserstein网络

2.1 Wasserstein自编码器

Wasserstein自编码器[19](Wasserstein auto-encoder,WAE)将VAE和生成对抗网络(generative adversarial network,GAN)结合在一起,能描述轴承真实振动数据分布的多样性。

WAE的模型架构如图3所示。

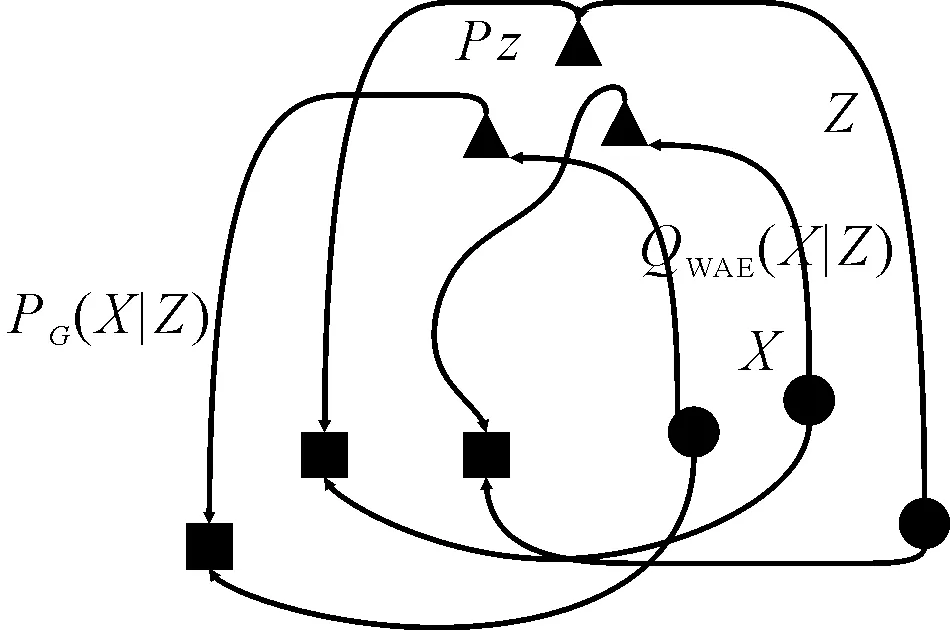
图3 WAE架构X—输入数据;PX—输入数据的概率分布;Z—隐层特征;PZ—隐层特征Z的先验分布;PG—重构数据的概率分布;PG(X|Z)—Z生成X的生成模型;Q(Z|X)—X生成Z的编码模型

对从PX中取样的输入样本X,WAE使QZ匹配PZ(如图3圆形),进而使不同样本的隐层特征相距较远,以便更好地进行重构。WAE的目标为最小化PX和PG之间的距离,其定义如下:

(9)

式中:c(X,Y)—损失函数。

上式可进一步分解为:

(10)

式中:DZ(QZ,PZ)—最大均值误差(maximum mean discrepancy,MMD)的正则项。

令DZ(QZ,PZ)=MMDk(PZ,QZ),则MMDk(PZ,QZ)可通过下式计算:

(11)

式中:k()—再生核函数。

Wasserstein网络(WN)堆叠多个WAE,首先,笔者利用无标签样本训练第一层WAE,得到第1隐层特征;其次,将第1隐层特征输入第2层WAE,得到第2隐层特征;以此类推;最后,利用少量带标签样本对整个网络进行有监督微调。

Wasserstein网络如图4所示。

图4 Wasserstein网络

2.2 自组织策略

在训练过程中,普通Wasserstein网络结构固定不变,对于非线性和非平稳性振动数据的识别效果还有待提升,因此,笔者引入自组织策略,使Wasserstein网络在训练过程中能自适应动态变化。

首先,在预训练阶段,将隐层节点激活强度作为节点“贡献度”,并根据“贡献度”大小对节点进行增加或删减;然后,在微调阶段,当损失函数梯度下降率首次出现递减时,删掉一个隐层,否则增加一个隐层。

激活强度S计算如下:

(12)

式中:α—常数;oi.l—第l个隐层的第i个节点的输出;Nl—第l个隐层节点个数;si.l—第l个隐层的第i个节点的输入权值之和。

si.l计算如下:

(13)

式中:rij—第i个节点的第j个输入;wij—第j个节点和第i个节点的连接权重。

详细的自组织策略步骤如图5所示。

图5 自组织策略

综上所述,基于ISSEWD-SOWN的滚动轴承工况识别步骤如下:

(1)采集不同工况下的滚动轴承振动信号,随机选取80%作为训练样本,其余为测试样本;

(2)对样本进行ISSEWD分解,并利用综合评价指标对本征模态分量进行信号重构;

(3)将重构后的训练样本输入SOWN进行无监督预训练和有监督微调;

(4)使用测试样本对训练好的网络进行测试。

工况识别流程图如图6所示。

3 实验验证

3.1 实验数据描述

为了验证所提出算法的有效性,笔者以XJTU-SY滚动轴承数据集[20]为实验对象,其轴承试验台如图7所示。

图7 XJTU-SY数据集试验台

试验所用的轴承测试平台由:交流电动机、电动机转速控制器、转轴、支撑轴承、液压加载系统和测试轴承等组成。试验平台可由径向力和转速调节工况,径向力由液压加载系统产生,转速由转速控制器调节;试验轴承为LDK UER204滚动轴承。

限于计算资源,本文在XJTU-SY数据集中选取10种不同的轴承运行工况,如表1所示。

表1 10种轴承工况

滚动轴承10种运行工况下的时域图如图8所示。

图8 滚动轴承10种工况的时域图

3.2 信号分解

以图8中的工况c信号为例,笔者采用ISSEWD对其进行分解,其结果如图9所示。

图9 ISSEWD分解结果

同样,笔者采用原始EWD对其进行分解,其结果如图10所示。

图10 原始EWD分解结果

根据文献[14]4-5提出的综合评价指标,笔者对信号进行重构,并进行相应的时频变换。

ISSEWD时频图如图11所示。

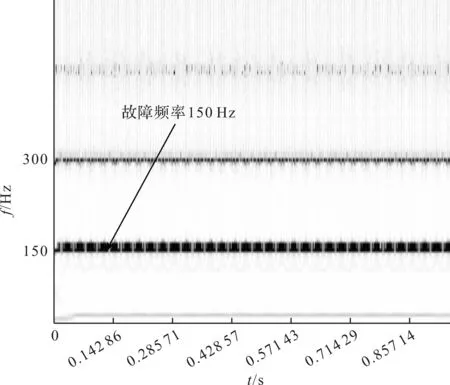
图11 ISSEWD时频图

原始EWD时频图如图12所示。

图12 原始EWD时频图

由图12可见:原始EWD分解结果IMFs分量众多,模态混叠严重;由轴承内圈故障特征频率计算公式可得工况c的故障特征频率约为150 Hz;从ISSEWD时频谱中可以看出故障频率以及倍频,从而验证了ISSEWD的有效性。

3.3 工况识别与分析

为验证ISSEWD-SOWN模型的效果,笔者采用不同模型进行对比。首先验证SOWN的效果,采用无自组织策略的WN、VAE、稀疏自编码器(sparse auto-encoder,SAE)和降噪自编码器(denoising auto-encoder,DAE)进行对比分析。

5种方法为:(1)ISSEWD-SOWN;(2)ISSEWD-WN;(3)ISSEWD-VAE;(4)ISSEWD-SAE;(5)ISSEWD-DAE。其中,SOWN的初始结构为2000-1000-500-200-100-10,WN、VAE、SAE和DAE的结构均为2000-1000-500-200-100-10。

5种方法10次实验的平均识别率如表2所示。

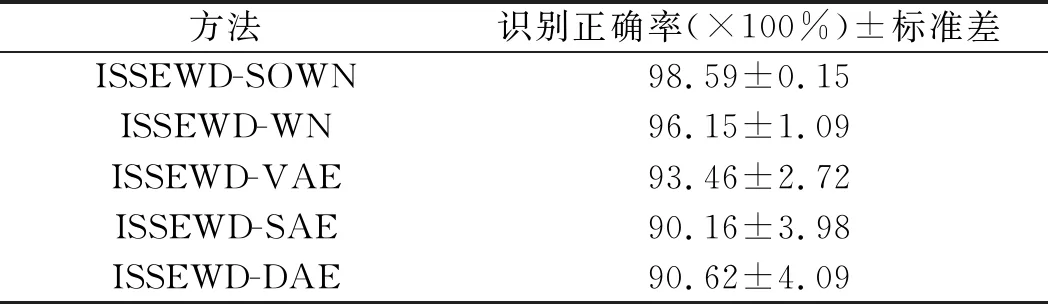
表2 不同方法的识别结果

由表2可知:(1)ISSEWD-SOWN方法具有更高的识别准确率(98.59%)和更小的标准差(0.15);(2)VAE将输入信号映射为一组特殊的概率分布,再从概率分布中随机采样得到隐层特征,这在一定程度上提高了其对环境噪声的鲁棒性,工况识别效果优于SAE和DAE;(3)WN将VAE和GAN结合,一定程度上克服了VAE学习到的特征的模糊性,能体现真实滚动轴承振动数据分布的多样性,识别效果优于VAE;(4)SOWN在WN的基础上引入自组织策略,使WN在训练过程中自适应动态变化,识别率更高。

为验证ISSEWD的效果,笔者采用不同的信号分解方法进行对比分析。其中涉及的方法有:(1)ISSEWD-SOWN;(2)EMD-SOWN;(3)EEMD-SOWN;(4)CEEWD-SOWN;(5)VMD-SOWN;(6)EWD-SOWN;(7)信号直接输入SOWN。SODN的结构均为2000-1000-500-200-100-10。

采用不同信号分解方法,10次实验的工况识别结果如表3所示。

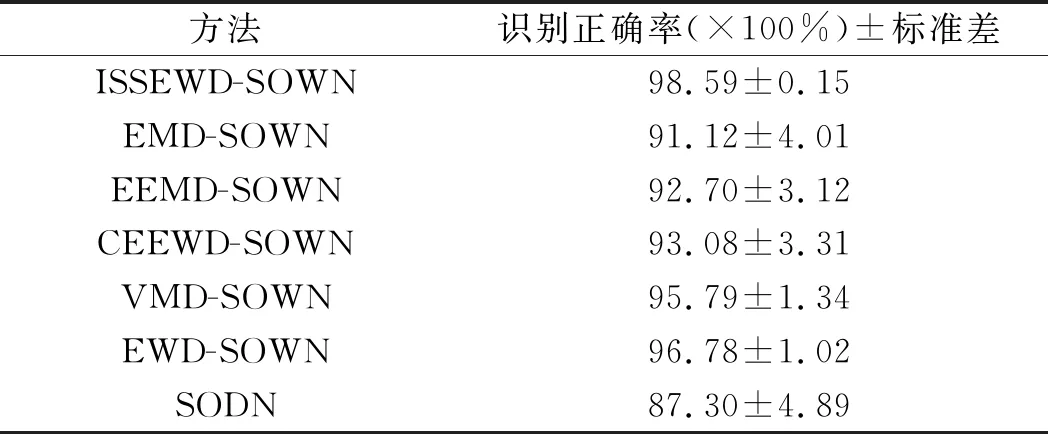
表3 不同信号分解方法的识别结果

由表3可知:(1)基于ISSEWD信号分解方法的识别率较其他方法更高,基于EMD、EEMD和CEEMD的信号分解方法模态混叠严重,存在较为严重的端点效应,导致工况识别率较低;(2)VMD和EMD一定程度上缓解了模态混叠和端点效应,具有较强的数学理论基础,识别效果优于EMD、EEMD和CEEMD;(3)若直接将原始振动信号输入SOWN,受噪声影响,工况识别率最低,仅87.3%;(4)ISSEWD方法使用四分位法,可有效地检测信号频率谱边界,能较准确地分解轴承振动信号,对噪声鲁棒性较强,工况识别率也最高。

3.4 不同比例的训练集对工况识别准确率的影响

训练集和测试集的样本比例对ISSEWD-SOWN的工况识别准确率有一定影响,若训练集样本比例过低,则会引起SOWN欠拟合;若训练集样本比例过高,则会引起SOWN过拟合;欠拟合和过拟合均会影响网络的识别准确率。

训练集样本占比60%～90%时,ISSEWD-SOWN模型的工况识别准确率如图13所示。

图13 不同比例的训练集对工况识别准确率的影响

由图13可知:在训练集样本占比60%～80%时,ISSEWD-SOWN的工况识别率随训练集样本所占比例的增加而增加;当样本占比超过80%时,工况识别率不再上升。因此,笔者选取80%的训练集样本。

3.5 不平衡数据集下ISSEWD-SOWN的识别率

为验证ISSEWD-SOWN模型在不平衡数据集时的有效性,笔者设计4种数据集,正常与各故障工况的样本比例分别为:8 000∶7 000;8 000∶6 000;8 000∶5 000和8 000∶4 000。

本文定量计算ISSEWD-SOWN、ISSEWD-WN和EWD-SOWN 3种方法基于不平衡数据集的F1值,即:

(14)

式中:TP—正样本中被模型判断为正的个数;FP—负样本中被模型判断为正的个数;FN—正样本中被模型判断为负的个数;F1—[0,1]之间,反映查准率和召回率的信息,0代表最差,1代表最好。

以组4为例,3种方法的F1值如表4所示。

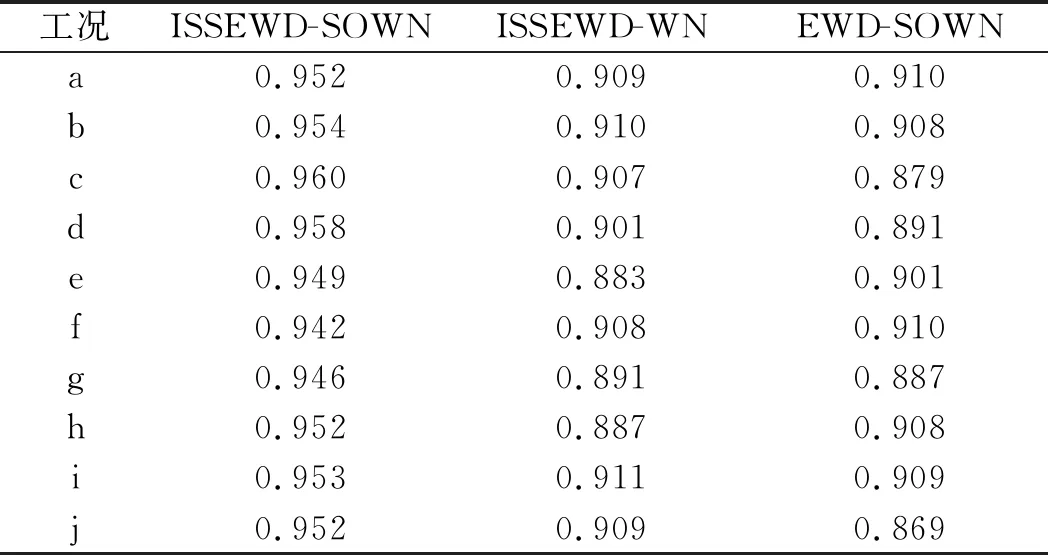
表4 组4不同方法的F1值

由表4可知:组4中ISSEWD-SOWN方法的F1指标值较高,类似的结果在其他组中也有较为明显的体现;该结果进一步验证了ISSEWD-SOWN在面对不平衡数据集时的有效性。

4 结束语

本文提出了一种基于ISSEWD-SOWN的滚动轴承工况识别方法,首先将采集到的滚动轴承振动信号进行了Fourier变换得到频谱,然后对其进行了分割,将滚动轴承振动信号分解为若干本征模态函数,筛选出最能反映轴承运行工况特征的IMFs进行了信号重构;构造了Wasserstein网络,引入了自组织策略,将重构后的振动信号输入自组织Wasserstein网络,最后进行了自动特征学习与自动工况识别。主要结论如下:

(1)提出一种四分位法检测滚动轴承振动信号频谱的边界,从而利用ISSEWD自适应划分信号频段自动确定分解模态数,克服了原始EWD易受噪声干扰的缺陷,能较准确地分解仿真信号和实际信号,鲁棒性较强,为后续SOWN自动进行特征提取和模式识别提供优秀的训练样本;

(2)提出的SOWN将自组织策略和WN结合,利用WN描述滚动轴承振动信号分布的多样性优势,结合自组织策略使WN在训练过程中自适应动态变化,识别率更高。

虽然该方法的识别准确率达到了98.98%,但在后续的研究中,笔者仍将进一步研究EWD更为有效的频谱分割算法和WN更有效的训练算法。