基于遗传算法风电场集电线路结构的优化
2021-06-19程谆,金焕,张阳
程 谆,金 焕,张 阳
(1.湖南铁道职业技术学院,湖南 株洲 412001;2.湖南工业大学,湖南 株洲 412007)
0 引言
风能作为一种自然界中的清洁能源,可无限地重复利用,依目前世界新能源发展情况来看,风力发电在全球范围内发展速度大幅度加快,风力发电产业以每年20%的增速不断向前发展[1-3]。主要的变速恒频机组可分为双馈型感应发电机和永磁直驱型同步发电机,永磁直驱型风力发电机与双馈型风力发电机相比,发电机省去了齿轮箱部分,因此具有发电效率高、可靠性高、运行及维护成本低等优点[4-6]。
风电场输电线路的连接方式可分为多种类型,如放射形连接、环形连接和星形连接,其中环形连接种类较多,可细分为单边环形、双边环形、复合环形以及多边环形4种[7-8]。但其连接方式较复杂,经济成本高,也会增加网络潮流分布的复杂性,使得潮流计算难度加大。而放射形网络的连接方式简单,投资成本低。综合考虑,放射形结构被广泛运用于风电场线路连接[9-11]。在风电场中,风机会被进行有效分组,在满足风资源分布和地形影响的情况下,风电机组的分组在一定程度上会遵循平均分配的原则,且必须保证各输电线路上最大输出容量满足单回输送容量的限制。
目前,关于风电场集电线路分组优化的研究较少。文献[12]则根据路径、导线、终端杆塔 T 接箱变方案以及山地风场特有的空气乱流影响等对山地风场集电线路进行优化设计;文献[13]通过建立线路投资费用折现函数模型、不同截面及长度线路造价模型、线路长度与线损造价模型、线路回数与造价模型,实现集电线路路径优化。传统方法在运用方面具有实用性不高、误差大、适用范围不广等缺点,为此,本文改变了线路等值模型和优化加权函数,提出了基于遗传算法的编程计算,使得计算更方便、更有效、更准确的得出优化后的线路分组。
1 风电场线路优化的目标函数
1.1 经济成本计算
由于本文主要的研究对象为风电场的集电线路,因此只对输电线路的经济成本进行计算,不计算风电场的总投资成本。线路成本等于单价乘以线路长度,同组风机与风机之间的距离取值都为1 km,每组离升压站最近的风机与升压站之间的距离为2 km,所以每组风机之间的距离可等效为此组线路上的风机台数再加 1。线路上的经济损耗C(x)可表示为:
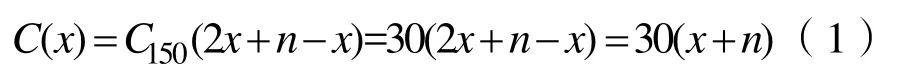
式(1)中x为风电场集电线路的组数,n为风机台数,C150为线路LGJ-150/25每千米的价格,其值为30万元。
1.2 阻抗等效计算
为了方便目标函数的建立,取线路阻抗的模值进行计算,其中线路LGJ-150/25的单位阻抗模值为0.443,每台风力机容量一致且为2MW,风电场线路组数为x,第i组线路上的风机台数为mi,计算过程如下:
首先计算同一组串联情况下的等效阻抗模值,其值为:
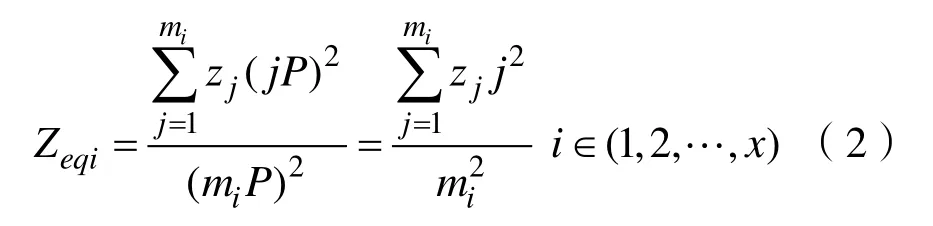
式(2)中,Zeqi为第i组串联情况下的等效阻抗模值,mk为第k组线路上的风机台数,zj为第j段线路上的阻抗模值,其中z1=z2=···=z8。将等效后的串联阻抗模值进行并联等效,求出最终风电场集电线路的等效阻抗模值,其值为:
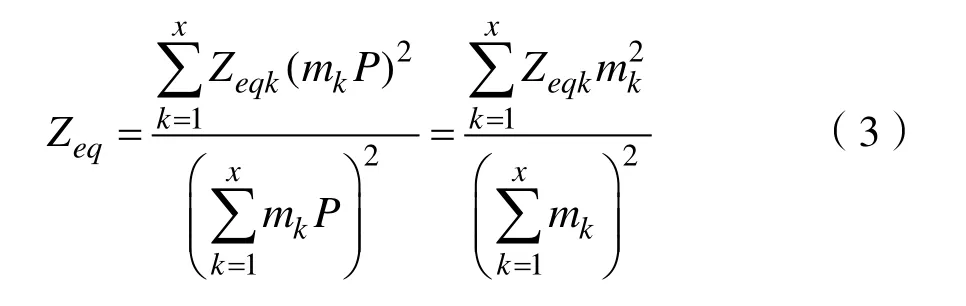
1.3 建立目标函数
在1.1和1.2中,已经计算出了本章风电场下的线路经济成本与线路的阻抗模值,因此接下来将需要结合两者建立目标函数来研究风电场线路在经济成本与等效阻抗模值两约束条件下的优化情况。由于两约束条件属于不同约束类型,将其归结为多目标优化问题,因此需对这两者采用归一化加权处理,通过权重系数来表示每个目标子函数在风电场建设中所占的重要程度。基于两种算法之间的对比,为保持一致性,并根据实际情况分析,在可保证一定安全性可靠性的基础上,线路经济性一般是被优先考虑的对象,因此将经济损耗所占的比例比线路阻抗值所占的比例稍高,在增强风电场供电可靠性的同时又满足在一定范围内的经济损耗。依然设阻抗值的加权系数为0.4,线路经济损耗的加权系数为0.6。目标优化加权函数为:
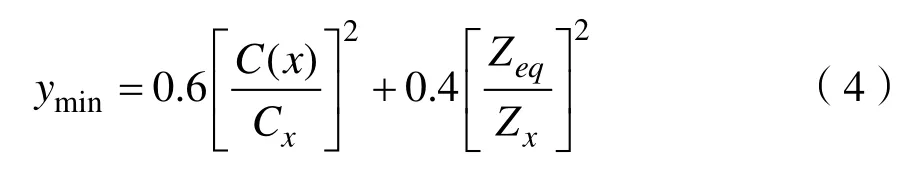
式(4)中,Cx、Zx指的是风电机组某种分组情况下的线路成本与线路等效阻抗模值。
本章节风电场对目标函数的约束条件为:

2 遗传算法实现
2.1 遗传算法流程图
根据式(4)的优化目标函数,使用MATLAB软件来编程,利用遗传算法对优化目标函数进行计算,得出仿真数据。首先读取本章目标优化函数模型的相关数据,建立目标函数,设置遗传算法参数与迭代最大次数maxgen。做好前期准备后,初始化染色体,建立优化目标范围内的初代种群且设置gen=0。接下来对初始种群采用十进制编码操作,完成从表现型到基因型的映射。当第一代种群产生后,需经遗传算法的两个基本操作变异与交叉完成后代的遗传,形成新的个体。随后将产生的种群个体解码成决策变量后代入到线路成本、阻抗计算与加权目标函数中,并计算出种群个体的适应度值,根据适应度的质量选择出优良个体准备下一代的遗传,完成第一次搜索之后进入不断地循环,直至达到算法迭代的次数,完成整个算法的运算,输出加权目标函数的最优结果与优化情况。利用遗传算法解决线路优化加权目标函数的流程图如图1所示。

图1 优化目标函数遗传算法流程图Fig.1 Optimal objective function genetic algorithm flowchart
2.2 运用的操作方法
2.2.1 编码操作方法
本遗传优化算法采用十进制编码法则,在优化目标函数模型数据中,风电场总风机台数为n,因此将算法编码长度设定为n,根据约束条件可知,线路组数为范围[1,10]的整数序列S。举个例子简要说明,如果总风机台数n=6,则其中某个符合条件的合法染色体可为[1,1,2,3,3,3],其意义为染色体数字代表第几组,有几个相同的数字就说明在此组上有几台风机,在染色体中有两个 1则表示第1组有两台风机,有一个2则表示第2组只有一台风机,有三个3则表示第3组有3台风机,以此类推。
2.2.2 基因变换
在此优化目标函数的算法中通过交叉与变异的两个操作方式来改变基因的变换,产生新的个体。对于交叉操作,采用了两点交叉的方式。而对于变异操作,则通过采用单点变异的简单操作。一下将对这两种方式进行简要举例论述。
(1)两点交叉
交叉对象发生在两个染色体之间,这两个染色体在上一代适应度强的个体中选择,随机选择其中两个染色体作为下一代的父本。在算法中根据算子产生两个随机自然数1r和r2,这两个自然数指的是染色体上的基因位数,决定所交换基因段的范围,即两父本染色体上的基因1r至r2位范围内的基因会相互交换,产生两个新的子代染色体。举例:假设两个父本个体(染色体)[1,2,2,4,1,3]、[2,3,3,1,4,2],其中r1=2,r2=3,那么交叉后产生的两个新个体为[1,3,3,4,1,3]、[2,2,2,1,4,2]。
(2)单点变异
单点变异是以某一个个体或染色体为基础的变异,在算法运行过程中,选择某个染色体,随后根据算子产生一个随机自然数1r,表示将在此染色体的第1r位的基因发生等位基因地突变。举例:假设个体[1,2,2,4,1,3]发生单点变异,变异的基因位置r1=4,那么个体[1,2,2,4,1,3]经变异后可能为[1,2,2,3,1,3]。
2.2.3 选择操作
在本章的遗传算法优化方式中的选择操作采用的是轮盘赌选择(又叫做比例选择算子),其基本思想是个体被选中的概率与个体的适应度质量有关,当个体的适应度越强,则个体被选中的概率也就越高,两者成正比的关系。假设种群个体数为n,将个体i代入适应度函数中求取适应度值iF,利用个体i的适应度值与整个种群适应度值的比值关系计算个体i被选中作为父代遗传给下一代的概率为:

某个种群的个体适应度与个体被选择的概率如表1所示,累积概率为前面个体被选择概率的和。另外个体的适应度的大小也可采用饼状图来直观的描述,将图形与数据结合,并将此饼状图当作轮盘通过旋转来选择个体,如图2所示,每个扇形面积表面的数据表示某个种群内个体的被选择的概率,个体适应度越强,扇形的角度与面积越大,轮盘指针停止在此面积上的概率越大。

表1 某种群个体示例Tab.1 Example of a certain group of individuals
图2 遗传概率饼状图Fig.2 Genetic probability pie chart
3 仿真结果与分析
在程序中输入相应的风电场风机台数n,计算出对应风电场满足目标函数的优化情况,个别计算数据如表2所示。
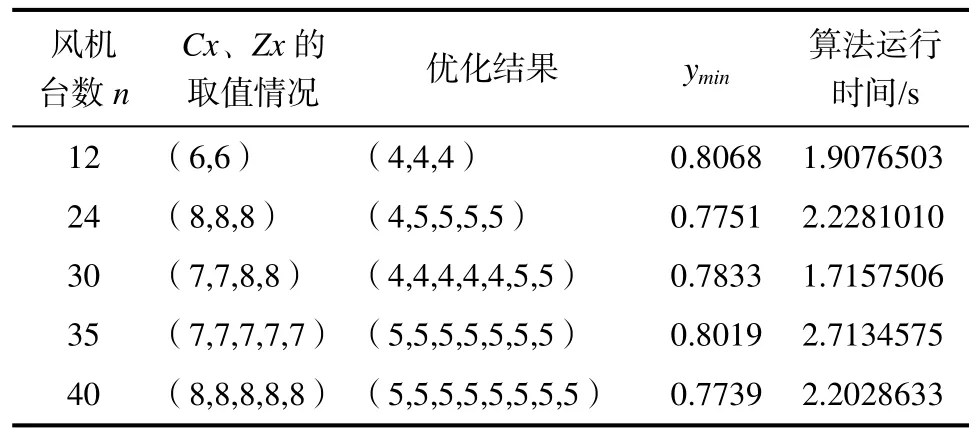
表2 优化结果Tab.2 Optimiz ation results
由表2可知,经仿真得出各台数风电场下的优化情况,从数据结果可看出当风电场台数为n= 1 2台风机时,优化后满足要求的分组情况为(4,4,4),即风电场线路被分为三组,每组四台风机;当n=24时,优化后的分组为(4,5,5,5,5),即风电场线路被分为五组,一组四台风机,四组五台风机;当n=30时,优化后的分组为(4,4,4,4,4,5,5),即风电场线路被分为七组,五组四台风机,两组五台风机;当n=35时,优化后的分组为(5,5,5,5,5,5,5),即风电场线路被分为七组,每组五台风机;当n=40时,优化后的分组为(5,5,5,5,5,5,5,5),即风电场线路被分为八组,每组五台风机。
从图3分析可知,在风电场风机台数n=12时,遗传算法经历了四次的转折变换,在迭代第35次左右后寻找到了最优值数据0.8068,并在往后的迭代次数中,加权值一直未发生变化。
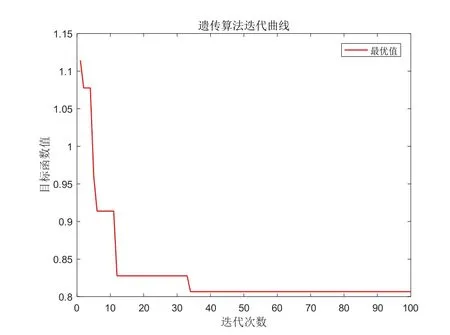
图3 n=12的迭代图Fig.3 Iteration graph withn=12
从图4分析可知,在风电场风机台数n=24时,遗传算法经历了五次的转折变换,在迭代第15次左右后寻找到了最优值数据0.7751,并在往后的迭代次数中,加权值一直保持不变。
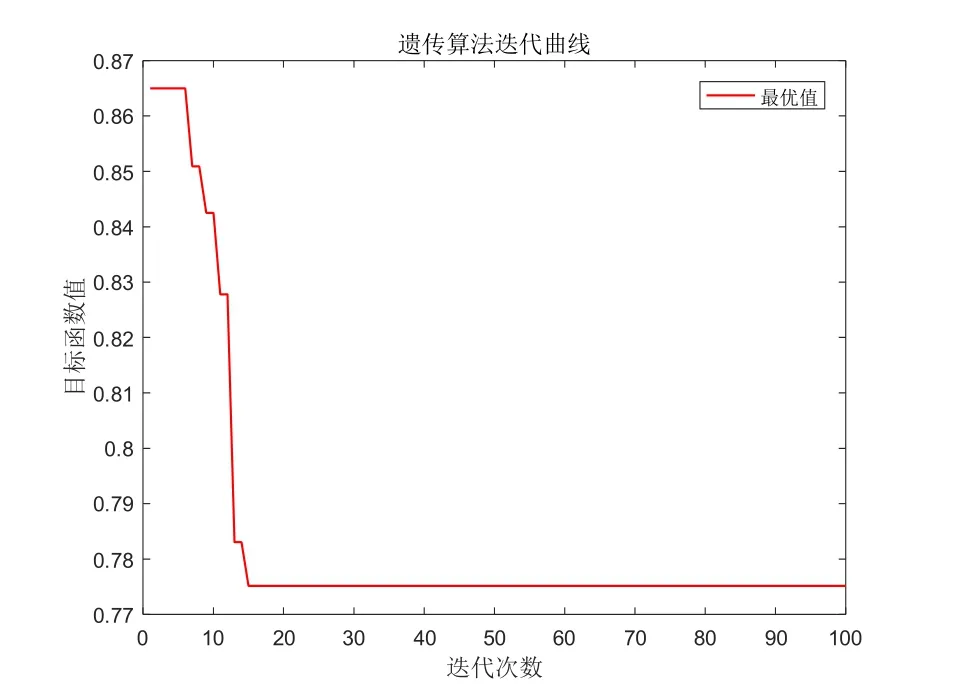
图4 n=24的迭代图Fig.4 Iteration graph withn=24
从图5分析可知,在风电场风机台数n=30时,遗传算法经历了四次的转折变换,在迭代第17次左右后寻找到了最优值数据0.7833,并在往后的迭代次数中,加权值一直保持不变。
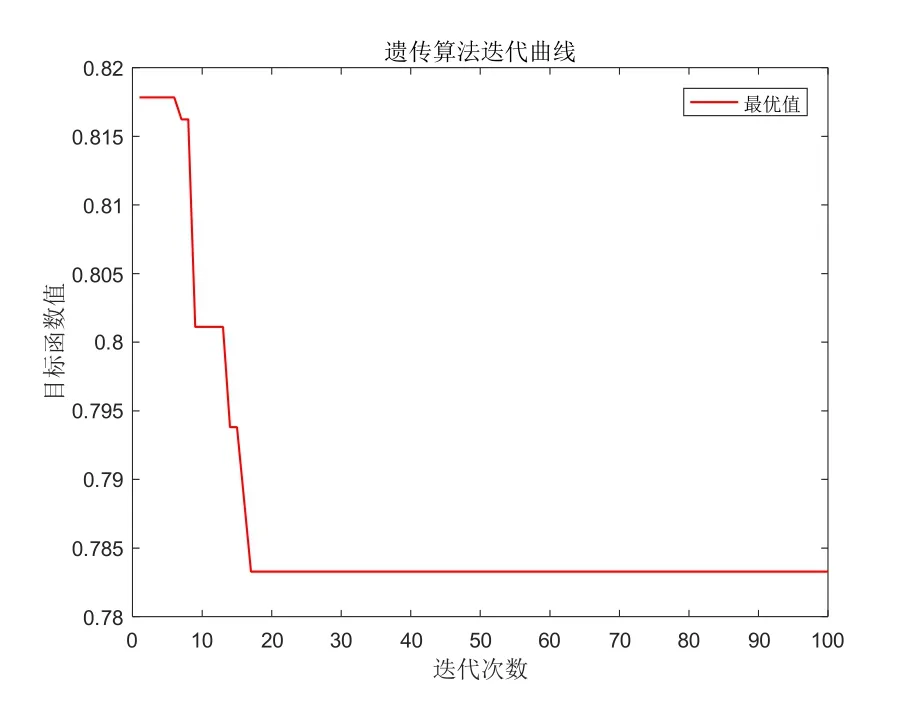
图5 n=30的迭代图Fig.5 Iteration graph withn=30
从图6分析可知,在风电场风机台数n=35时,遗传算法经历了五次的转折变换,在迭代第21次左右后寻找到了最优值数据0.8019,并在往后的迭代次数中,加权值一直保持不变。
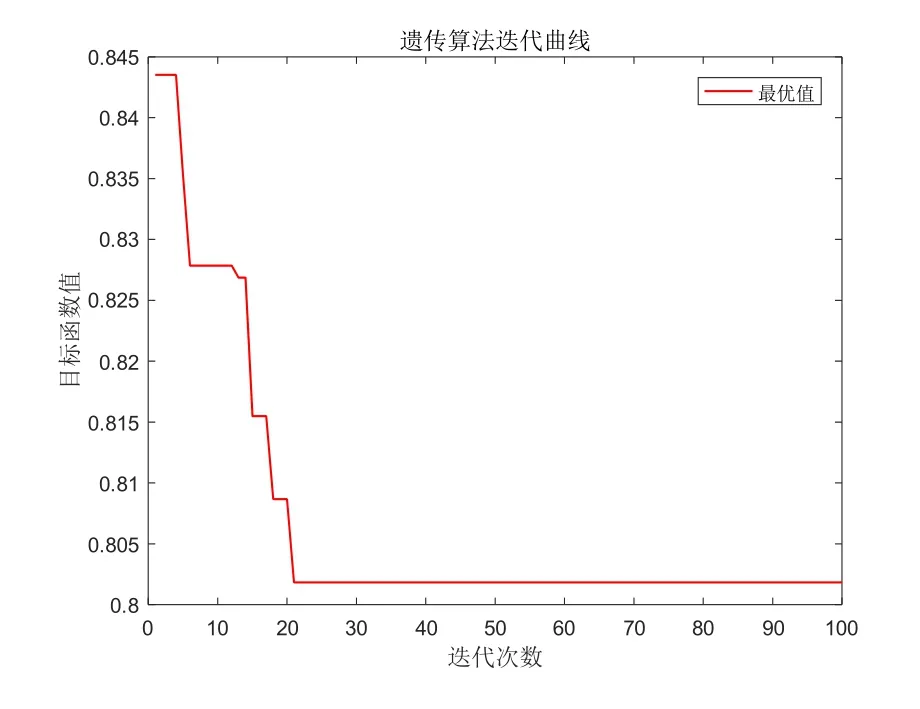
图6 n=35的迭代图Fig.6 Iteration graph withn=35
从图7分析可知,在风电场风机台数n=40时,遗传算法经历了四次的转折变换,在迭代第32次左右后寻找到了最优值数据0.7739,并在往后的迭代次数中,加权值一直保持不变。
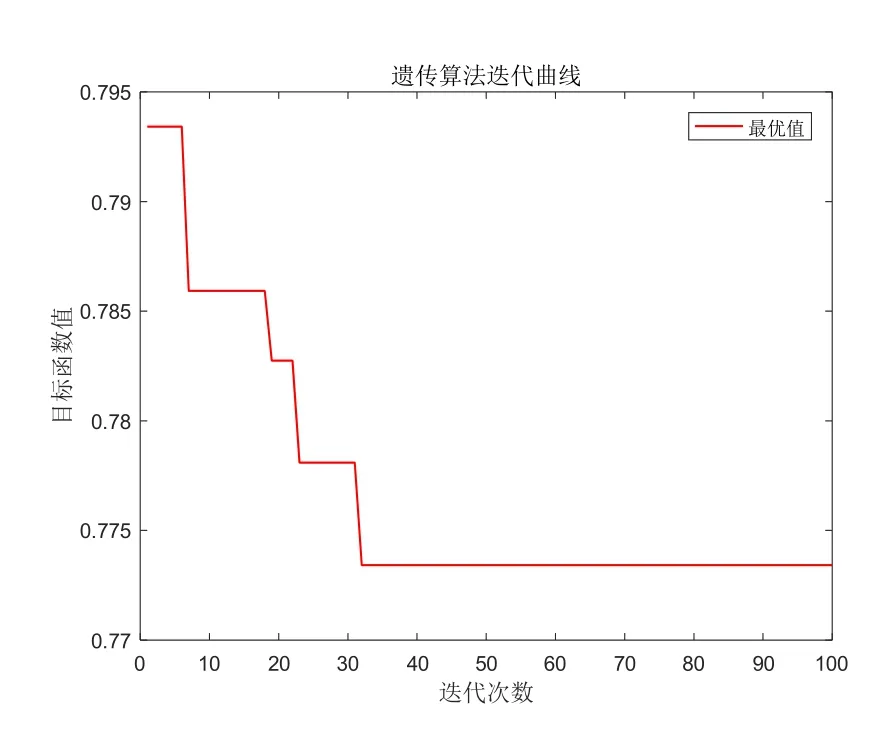
图7 n=40的迭代图Fig.7 Iteration graph withn=35
因此从运行计算时间可知,本次遗传算法计算所用的运行时间在3s以下,运行速度较快。并且从图3至图7的迭代图的迭代次数可知,因遗传算法并行运算的特性,加权函数的优化计算每次迭代的次数都在35次以下,使得能够快速寻找到最优值。
4 结论
本文首先介绍了遗传算法的原理与特点,然后建立了归一化加权目标函数,利用MATLAB软件编写遗传算法求解目标函数,采用了十进制编码法则,基本操作分别采用了两点交叉方式、单点变异方式和轮盘赌选择。最后仿真结果表明,本文所提方法计算出的优化数据具备准确性、快速性和实用性。
