基于聚类分析的群智感知任务分配

何杏宇，董一鹏，王 静，何 姝，陶 凝，杨桂松

(1.上海理工大学 出版印刷与艺术设计学院，上海 200093；2.上海理工大学 光电信息与计算机工程学院，上海 200093)

0 引言

群智感知（Crowd Sensing）是结合众包思想和移动设备感知能力的一种数据获取方式，通过在移动设备之间形成交互式的、参与式的感知网络，并将感知任务分配给网络中的个体或群体来完成，任务参与者通过分工合作实现感知任务的协同与感知数据的收集。当前，群智感知已应用于临床和心理实验的研究[1]、评估暴力人群[2]、道路异常检测[3]、空气质量监测[4]等多方领域中。

群智感知中任务分配方法具有两种模式：集中式感知和机会式感知。集中式感知是利用集中的蜂窝网平台来分配感知任务，支持实时感知数据的上传[5-8]。机会式感知是利用节点的机会式接触进行感知，在这种模式下感知数据可以延时传输[9-12]。群智感知具有部署灵活、感知数据多源异构、覆盖范围广泛均匀和高扩展多功能等特点，其中，提高感知覆盖范围，有助于获得较高的感知数据质量。虽然已有很多对感知覆盖度的研究[13-17]，但较少从结合集中式感知和机会式感知的特点角度来研究的。

本文发现，集中式感知的特点是可以根据预定的感知成本来选择合适的节点执行任务，通过优化节点的筛选机制来优化全局覆盖率，有利于保障感知质量和成本的全局可控性，但是难以根据不同区域节点覆盖率的差异性来调整感知成本在不同区域的分配情况。而机会式感知的特点是较难保障感知质量和成本的全局控制，但可以根据节点局部的实际覆盖质量来调整局部任务参与节点的个数，从而调节局部感知成本的分配情况。

因此，本文将结合上述两种感知模式，提出一种兼顾感知质量和成本的局部差异性及全局可控性的任务分配方法，并在该方法中引入聚类分析算法来对节点的移动范围进行分析。根据分析结果进行任务参与节点的选择，并通过实验对本文提出方法的性能进行评估和分析。

1 问题描述与网络模型

在本文的群智感知网络模型中，节点是移动的，群智感知任务将分配给两类节点：集中式参与节点和机会式参与节点。通过移动群智感知平台直接进行选择和分配获得感知任务的节点称为集中式参与节点，通过集中式参与节点的机会式接触来获得感知任务的节点称为机会式参与节点。网络中感知任务是由这两类节点来协同完成的，首先由网络平台将任务发布给选中的集中式参与节点，集中式参与节点获得任务后会在其移动范围内执行感知任务，并在其遇到机会式参与节点之后将任务复制并传递给机会式参与节点。

1.1 节点移动范围

为了能够对群智感知网络中节点的移动范围进行描述和分析，本文将网络分成多个互不重叠的分区，然后将每个分区按顺序进行标号(A1,A2,A3,…,Ai)，如图1所示。

图1 网络分区示意图Fig.1 ne twork partition

假设网络中共有m个节点，节点用Ni表示，这m个节点的集合表示为N={N1,N2,N3,…,Nm}。网络中每个节点的移动范围与其工作模式和社会属性相关，因此具有固定模式。如图1所示，圆点表示任意节点Ni，三角形所在分区表示此节点的移动范围，则节点Ni的移动范围可以表示为分区集合Mi={A2,A5,A6}。如果一个节点被选为参与节点，它可贡献的感知覆盖范围为该节点的移动范围。本文的目标是在控制参与节点数量的前提下最大化两类节点所贡献的总感知覆盖范围。

1.2 移动范围相似度分析

由于集中式参与节点和机会式参与节点之间需进行任务传递，要求这两者具有接触机会，也就是说需要节点之间有重叠的移动范围。为了对此进行判断，本文定义了节点之间的移动范围相似度，用Si,j来表示节点Ni与Nj的移动范围相似度，其计算方法为：

其中Si,j∈[0,1]。需要注意的是，当Si，j=0时，Ni与Nj移动范围不存在重合部分，此时任务无法在Ni与Nj之间传递；当Si,j≠0 ，Ni与Nj移动范围有重合，则它们互相成为亲密节点。用Fi表示节点Ni的所有亲密节点集合。对于节点Ni与Nj，本文使用num(Fi∩Fj)表示他们之间的共同亲密节点数，并且设置了一个共同亲密节点数量阈值K。本文将在后续算法中通过判断num(Fi∩Fj)与K的关系对节点进行分簇。

1.3 感知覆盖范围分析

在任务分配中，本文通过局部的覆盖率差异性来调节局部的成本分配情况。根据网络中节点的移动范围相似度将节点分成多个簇。假设预设总任务参与节点个数为Q，形成的簇总数为T，且节点个数和成本在这T个簇中平均分布，那么每个簇都可以均衡选择Q/T个任务参与节点。实际上由于节点个数和感知质量的局部差异性，每个簇选择的机会式参与节点个数也可能不均匀，其值等于[Q×n/m]，其中n为簇内节点个数，m为网络总节点个数。

用V={C1,C2, …,CT}表示簇的集合，簇Ct贡献的感知覆盖范围与其簇头的选择有关。也就是说，Ct的簇头不同，其感知覆盖范围也将有所不同。例如，当Ni作为Ct的簇头时其贡献的感知覆盖范围可以用表示，它是Ni的移动范围以及Ni选择的机会式参与节点的移动范围的并集。假设根据Ni选择的机会式参与节点为N1,N2,…,Nh，则的计算公式为：

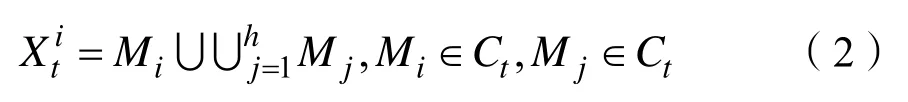
若所有任务参与节点存放在集合Ω中，那么所有的任务参与节点所贡献的总感知覆盖范围用R表示，其计算公式为：

从（3）可以看出，如果想要在控制参与节点数量（成本）的情况下使总感知覆盖范围达到最大，既需要单个任务参与节点的移动范围尽可能大，又需要节点间移动范围的重合度尽可能小。

2 算法设计与分析

算法 1所示，为了使集中式参与节点之间具有较大的移动范围相异性，并且保障集中式参与节点与机会式参与节点之间的相遇机会。本文利用聚类分析对网络中节点的移动范围进行分析，并对其进行分簇，使同一簇内节点具有相似的移动范围，不同簇的节点之间的移动范围具有较大相异性。

算法 1在进行集中式参与节点选择的同时进行机会式参与节点选择，在机会式参与节点选择时，兼顾它们与同簇集中式参与节点之间的移动范围相似性和相异性。

在每个簇中，簇头应该具有较广的移动范围，它将被选择作为集中式参与节点接受集中平台分配的感知任务，并负责其簇内的机会式任务分配，簇中除了簇头以外的节点被称为簇成员，它们中的一些节点将会被选择为机会式参与节点。

2.1 基于移动范围的分簇

算法1依次选择节点集合N中的节点，对所选节点之间的共同亲密节点数量进行分析。本文以Ni和Nj为例，如果num(Fi∩Fj)大于K，则存在三种分簇处理情况：如果Ni和Nj目前都未并入任何簇，则生成一个包含Ni和Nj的新簇；如果Ni或Nj已经属于一个已有簇，则将Ni和Nj并入该已有簇；如果Ni和Nj分别属于两个已有簇，则将两个簇合并。当该算法对N中的所有节点都执行了上述与亲密节点有关的聚簇分析，则该算法的分簇过程结束。

当上述算法的分簇过程结束，将会形成多个簇，这多个簇的集合用V来表示，N中的节点分别归属这些形成的簇。上述算法将从每个簇中选择能使得该簇的感知覆盖范围最大的节点作为簇头。

2.2 任务参与节点选择

算法1中，每个簇的簇头为集中式参与节点，在选取簇头的过程中也同时进行了机会式参与节点的选择。例如，当Np作为Ct的簇头时该簇的感知覆盖范围为，给定Up表示Np和根据Np选择的机会式参与节点的集合。表1所示算法首先将Np并入Up，然后依次选择机会式参与节点并入Up，且它每次选择机会式参与节点需要满足三个基本条件。1）此节点应该位于Ct中；2）此节点需要使实现最大化增加且使局部覆盖质低于预设值w（该预设值等于总网络范围除以总节点个数）；3）最大个数少于[Q*nt/m]。例如，假设选择的机会式参与节点为Nq，在满足上述条件的基础上还应满足Nq的移动范围与的交集最小，将Nq并入Up中，并更新当选择的机会式参与节点总个数为[Q×nt/m]或局部覆盖率质量高于预设值w，以Np为Ct簇头时的机会式参与节点选择完毕。值得注意的是，如果机会式参与节点选择过程中被选择节点的所有移动范围都已被覆盖，则不应选择该节点作为机会式参与节点。

上述在选择集中式参与节点的同时选择机会式参与节点只是预选方案，而被选择的集中式参与节点将携带预分配的成本移动，当其遇到预选择的移动式参与节点时将任务分配出去（实际也有可能没有遇到预选择的移动式参与节点）。

表1 基于聚簇分析的任务参与节点选择算法（算法1）Tab.1 Task participation node selection algorithm based on cluster analysis (Algorithm 1)

3 实验设计与分析

为了评估所提出算法的性能，本文利用文献[18]中的数据集进行了仿真实验，此数据集是由182个用户在五年多的时间中收集到的，包括用户的17 621条轨迹信息。本文将数据集的网络划分为25个分区，并随机选择网络中100个用户节点进行实验。这些实验中主要考虑4个不同的参数：1）网络分区的数量；2）网络中节点的数量；3）选择的任务参与节点数上限Q；4）节点共同亲密节点数量阈值K。通过设置任务参与节点数上限Q来控制实验中最多可选择的任务参与节点数，而阈值K则是分簇的关键条件。用P表示最终的覆盖率，其等于总感知覆盖范围R中分区数量与总分区数25的比值。

3.1 性能对比

在机会网络中进行机会式参与节点选择的最基本算法为Epidemic算法[19]，即平台将任务发布给一个集中式参与节点，然后此节点将任务复制给它接触到的所有节点。为了验证本文所提出算法的优势，将其与Epidemic算法和文献[20]中的集中式ILB算法进行对比。在比较这三种算法时，固定阈值K的值为0，调节任务参与节点数上限Q，比较三种算法最终的覆盖率大小。为了避免实验的偶然性和随机因素带来的影响，针对同一个参数进行一百组实验，取平均值作为最后的结果，对比结果如图2所示。

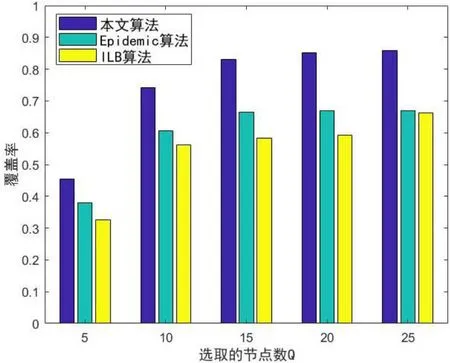
图2 覆盖率对比（K=0）Fig.2 Comparison of coverage ratio

由图2可以看出在阈值K和节点数上限Q一定时，本文算法能达到的覆盖率明显高于其余两种对比算法，说明本文的算法在有成本限制的情况下提高覆盖率方面具有较为明显的优势。

3.2 参数K和Q对本文算法的影响

由于任务参与节点的选择和分簇是密切相关的，而实验中对分簇起关键性作用的是阈值K，K不同则分出的簇中包含的节点也不同，因此最后的覆盖率也会存在差异。本文将阈值K和节点数上限Q分别设置为：K=[0, 1, 2,…, 10]、Q=[5, 10,15, 20, 25]，每组参数均进行100组实验，通过多次实验取平均值的方式，计算覆盖率与阈值K的关系，如图3所示。

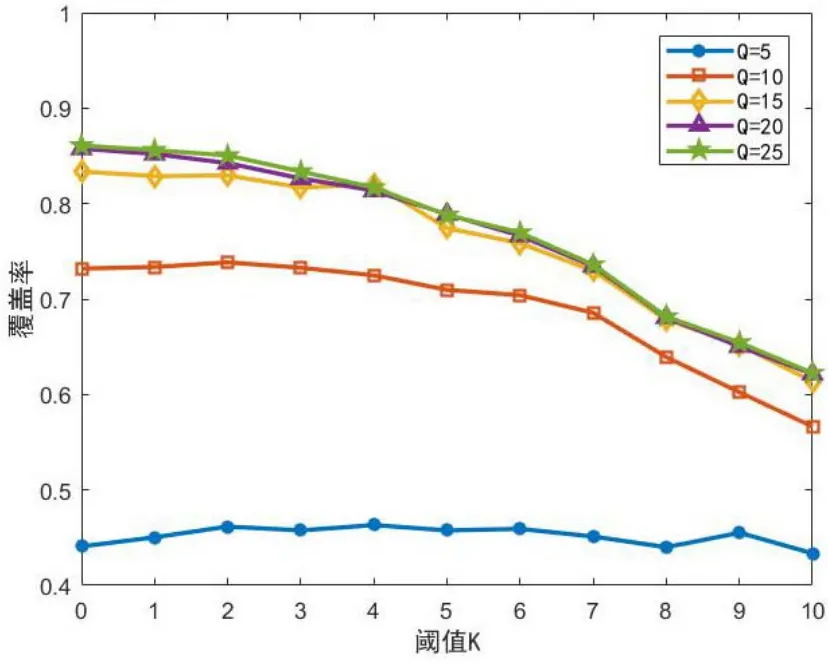
图3 覆盖率与阈值K的关系Fig.3 Relation between coverage ratio and K

由图3的实验结果可以看出，在阈值K≤3时覆盖率处于一个较高的水平，当K＞3时随着K值的增大，曲线整体处于一个下降的趋势，这是因为如果K值较大，会使得某些节点变成孤立节点。虽然孤立节点能够扩大覆盖率但是本文不会选择其作为集中式参与节点，因为其不能将任务复制给机会式参与节点，因此当阈值K过大时会导致覆盖率降低。同时本文发现当Q=15和Q=20时覆盖率处于一个较高水平，而当Q=5时覆盖率处于一个过低的水平，而Q=25时覆盖率基本上不再增加。这说明如果选择的节点过少，会导致覆盖率无法达到一个较高水平，选择的节点过多则会使成本增加但无法增加覆盖率。据此本文通过固定K，改变Q的值进行多次实验，结果如图4所示。

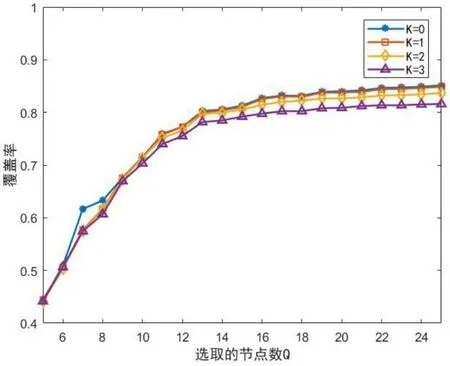
图4 覆盖率与节点数上限的关系Fig.4 Relation between coverage ratio and K and the number threshold of nodes

由图4可以看出，当阈值K不变时，在节点数Q＜12的情况下，随着节点数Q的增大，覆盖率会有较大幅度的增加，当Q≥13时覆盖率的增加幅度变缓，这说明当选择的节点数过小时覆盖率无法达到一个较高水平，而如果选择的节点数过多，则会导致成本不断增加而覆盖率几乎不再增长。从实验结果中可以看出当Q的值在13到19之间时，覆盖率能够增长到一个最高水平，此时不宜选择更多的参与节点。

4 结论

本文研究了一种兼顾感知质量和成本的局部差异性和全局可控性的任务分配方法。本文首先对网络中所有节点的移动范围进行聚类分析以进行分簇，然后选择使簇的感知覆盖范围最大的节点作为集中式参与节点，再从簇中选择与集中式参与节点有相遇机会且能够扩大簇的感知覆盖范围的节点作为机会式参与节点。通过实验对比了本文算法、Epidemic算法和ILB算法的性能，发现在具有成本限制的情况下本文算法能达到的覆盖率明显优于其余两种算法。此外，实验结果还揭示了参数K和Q对本文算法产生的影响。本文下一步将利用除了移动范围以外的更多特征来对节点进行聚类优化。