Disassembly Sequence Planning: A Survey

Xiwang Guo,, MengChu Zhou,, Abdullah Abusorrah, Senior,Fahad Alsokhiry,, and Khaled Sedraoui

I. INTRODUCTION

INDUSTRIAL products significantly improve human living standards and promote social progress. Meanwhile, they generate a large amount of industrial waste, which threats the ecological environment and human health. With the increased discarded products in recent several years, their recycling can help us achieve sustainable industrial development by reducing environmental pollution and waste resources. They put great pressure on the ecological environment if they are improperly handled. According to the prior studies [1]–[6],70% of the environmental pollution is caused by waste materials from manufacturing enterprises. About 5.5 billion tons of dangerous materials and 700 million tons of hazardous materials are generated each year. The ecological environment and natural resources can thus be seriously damaged by the improper handling of these discarded products.

In order to alleviate the harm to the ecological environment and deterioration of natural resources, remanufacturing,recycling and reuse of discarded products have attracted much attention from engineers and scholars around the world. A reverse production chain is one of the main methods to solve the aforementioned problem. It involves disassembly, inspect,shredding and separation. The components/parts and subassemblies from end-of-life (EOL) products are usually utilized within the reverse production chain. Hence, a framework of the reverse production chain involves: 1) product remanufacturing, 2) materials recycling, 3) component reuse, and 4) final disposal, which includes incineration and landfill. A closed-loop supply chain (CLSC) is shown in Fig. 1.It includes raw and auxiliary materials supplier selection,product partners’ evaluation, inventory management, market demand, disassembly planning, transportation distribution,reverse logistics, and CLSC design. It is shown that disassembly is a critical operation in CLSC since recycling,remanufacturing and reusing require the disassembly of EOL products. Effective disassembly sequence planning (DSP) can recover already-used yet valuable components for other products. A disassembly sequencing problem determines how EOL products are disassembled to retrieve discontinued products to meet a sudden demand for products, parts and/or materials such that a variety of objective functions are optimized, and constraints are met.

Disassembly can extract useful components/parts and materials from EOL products through a series of operations with the following advantages: 1) It can achieve resource recycling of EOL products; 2) some components can be reused; and 3) it can dispose separately of those parts with harmful substances, e.g., environmental pollutants.

Although the disassembly of EOL products has the above advantages, the modern optimization theory and methods are not fully used in recycling and remanufacturing enterprises.This work is aimed to intensively study DSP problems by providing the theory and advanced methods for the recycling of discarded products in a disassembly process.

This paper aims to present a survey of DSP literature. A disassembly sequence is a list of orderly disassemblyoperations. An assembly can be separated in two or more subassemblies, or one or more connections between components by an operation. Generally, an assembly can be broken down into many components via a multitude of operation sequences, which makes the selection of an optimum sequence a crucial topic in this remanufacturing field.

TABLE I COMPARISON OF EXISTING SURVEY PAPERS

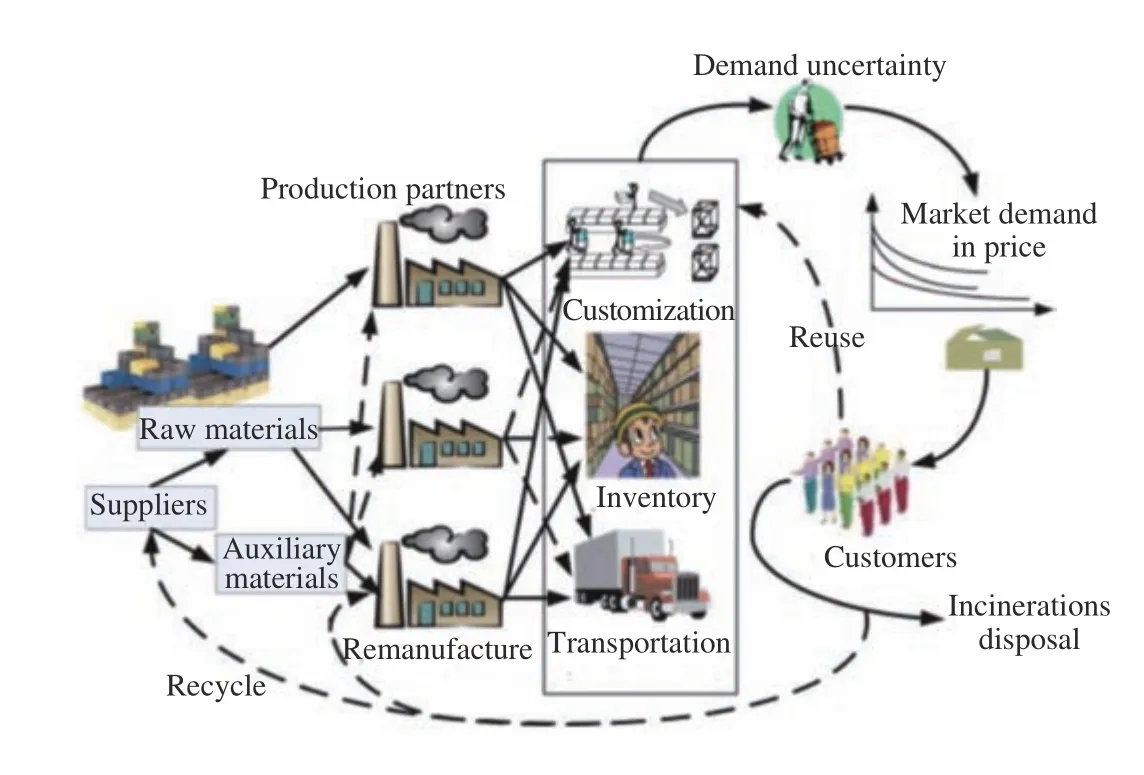
Fig. 1. Closed-loop supply chain (CLSC).

Six survey papers have focused on DSP. The first one is [7]that presents a concise survey paper and discusses 33 papers up to the year of 1998. The second one is [8] that reviews the state-of-art papers’ topic in the field of disassembly sequencing. The third one, by Ilgin and Gupta [9], discusses 546 papers up to the year of 2010, from which about 50 papers are related to DSP. The fourth one, by Ilginet al. [10],discusses 229 papers up to the year of 2015, from which about 42 papers are related to DSP. The last one, by Zhouet al. [11],discusses 159 papers about DSP up to the year of 2018. The comparison of the aforementioned studies is summarized in Table I.

In this survey, we classify methods according to main characteristics and solution methods of DSP problems. Due to existing theoretical challenges and practical disassembly technology applications, various disassembly problems have been solved by many researchers such as disassembly design[12], disassembly method, disassembly line balancing[13]–[22], DSP, and lot-sizing disassembly problems [23]–[25].

Many recent papers remain to be surveyed. According to[26], most of the existing studies investigate DSP in three main steps: 1) a particular expression tool is used to formalize the dynamics of a disassembly process, e.g., AND/OR graph,tree, Petri-net, matrix-based representation and state representation; 2) a “cost structure” is assigned to a representation and models the economic elements involved in a decision-making process; and 3) a method is applied to select the best disassembly sequence by means of the established framework in the first two steps. A deterministic model is assumed by most of the existing work on optimal DSP for the underlying process dynamics and cost structure. This work intends to make the following contributions:

1) It attempts to discuss journal and conference papers with an emphasis on recent work. Scholars and engineers investigate DSP with a diversity of interests. This review presents an analysis of disassembly sequences to help decision makers engage in product recovery and reuse activities. Over 100 scientific papers published between 2007 and 2020 are reviewed in this work.

2) Modeling methods include graphical ones such as graphbased modeling, AND/OR graph, Petri nets and matrix-based models. All the possible disassembly sequences can be generated by using these modeling methods. This is followed by the search for reasonable and optimized disassembly sequences, which can be done according to heuristics. In addition, the advantages and disadvantages of these modeling methods are summarized.

3) Mathematical programming and optimization methods are presented, which are the main content of this paper. AI methods are also discussed to solve a DSP problem, for example, genetic algorithm (GA), ant colony optimizer,scatter search (SS) and particle swarm optimizer. Their advantages and disadvantages are summarized in this work.

4) In an EOL product, uncertainty plays an important role.Physical properties of the connections are considered, for instance, friction, or simply by restricting the number of degrees of freedom. Uncertainty theory and methods are discussed and used to solve a stochastic DSP problem.

Section II describes modeling methods. Section III introduces the MP methods. Section IV presents intelligent optimization algorithms. Section V gives uncertainty analysis.Finally, our work is concluded and some future research issues are described in Section VI.

II. MODELING METHODS

Product representation and modeling are essential for successful product disassembly sequencing and operations.Some factors influence a feasible disassembly sequence such as components’ relationships, constraints of removing a component, a product’s geometric structure, a hazardous feature of disassembly, tools required in operations, space accessibility for tools, the condition of the returned products and complexity of components and fasteners to be removed to disassemble target components. The feasibility of a disassembly sequence is dependent on a product structure. A representation of a product structure directly affects the efficiency of a disassembly sequence search. Xieet al. [27]developed a graph-based modeling method of product representations for DSP. Simulated annealing and GA were used to obtain the near-optimal solution (disassembly sequence). Behdad and Thurston [1] employed integer linear programming based on a graph representation combined with multi-attribute utility analysis to identify the best set of tradeoffs among disassembly times under uncertainty. A solar heating system was used to illustrate the effectiveness and feasibility of the proposed method. The details of a product structure, components, constraints and connections are described by the product representation [1]. Luoet al. [28] presented a disassembly operation such that a failed component of a product could be replaced for maintenance, or reusable components of an EOL product could be recycled to reduce its impact on environments and maximize the utilization of reusable resources. Fenget al. [29] proposed a disassembly process information model for describing a disassembly process, which could serve as a foundation for computer-aided disassembly software systems. Ullerich and Buscher [30]proposed a mixed-integer linear program based on a disassembly state graph for optimal sequencing and ensured the feasible operations of product disassembly. Zhaoet al.[31] proposed a reasoning algorithm to identify a product disassembly sequence with fuzzy reasoning Petri nets. The algorithm utilizes the matrix operation to calculate the disassembly sequences. Their experimental results show that their model has a strong parallel operation ability in dealing with DSP.

A disassembly planning system includes three basic elements such as product representation, sequence search, and solution optimization. Disassembly sequence search is conducted based on a product representation.

In this section, graph-based modeling, AND/OR graph modeling, Petri net (PN) modeling and matrix-based modeling methods are described. A comparison of the modeling methods is summarized in Table II.

A. Graph-based Modeling

Graph-based modeling aims to describe the component relationships of an EOL product. It includes more component constraint information about a product structure. Graph-based modeling tools include undirected or directed graphs. In this paper, a component also represents a subassembly. In the early study of DSP, the generation and optimization of a disassembly sequence are mainly based on graph theory. A graph consisting of nodes and edges is used to describe the precedence relationship among components in products.Usually, a node represents a component; and the edges that connect nodes represent the relationship between various components. A disassembly sequence and the constraints of a product are expressed by a graph. Based on the graph, a disassembly sequence can be identified.

Kuo and Wang [32] adopted graph-based method to describe the precedence relationships among different components in a product. Zhanget al. [33] adopted a graphbased method to represent a dishwasher for disassembly planning. Songet al. [34] developed another type of graphs,named as an adjacent graph to describe a product.

Behdad and Thurston presented a graph-based integer linear program combined with multi-attribute utility analysis [1], [2].It is employed to identify the best set of tradeoffs among a)the probability of failure during disassembly; b) disassembly time under uncertainty; c) reassembly time; and d) the probability of failure during reassembly.

An undirected graph describes the assembly relationship among components. It can be expressed asG= (V,E), whereVis a set of nodes, representing the components to make up a product; andEis a set of edges, representing adjacencies among the components.

Take a product shown in Fig. 2 as an example. We can construct an undirected graph, as shown in Fig. 3. It has 6 nodes (components) and 9 edges for their adjacency relations.

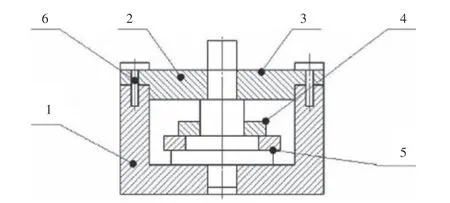
Fig. 2. The connection structure graph of an assembly.

Fig. 3. The undirected graph of a product in Fig. 2.

A directed graph model of a product can be expressed byG'= (V,E), whereVis the set of nodes, representing the components of a product;Eis the set of directed edges,representing the precedence relationship between the components. An example is given as shown in Fig. 2, we can construct a directed graph as shown in Fig. 4, where the nodes and edges mainly record the geometrics, constraints, and joint information of product components. Yet it is difficult to generate such a graph from product design information automatically. It can only be used for a product with a simple structure and a few components. Otherwise, it becomes very complicated.

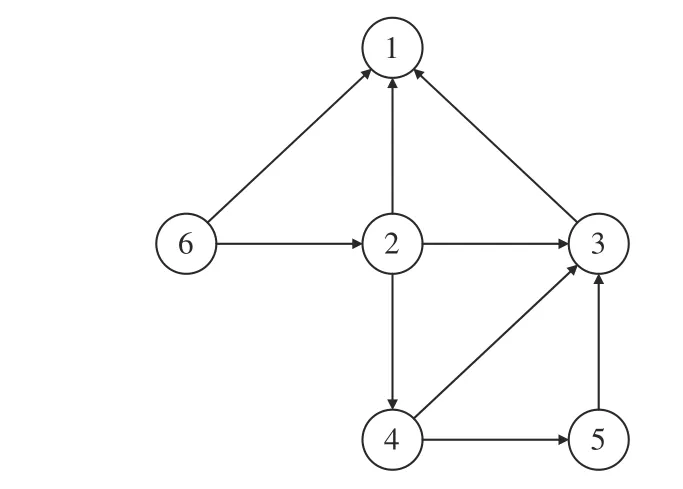
Fig. 4. The directed graph of a product in Fig. 2.

B. AND/OR Graph Modeling

AND/OR graph is an important representation method in DSP. It can express the disassembly information of components. It not only expresses a DSP problem among components, but also effectively expresses the logical combination relationship among the components. The disadvantage is that as the number of components increases, it is easy to produce a phenomenon of combination explosion.G=(V,E) represents a disassembly AND/OR graph. The set of nodes is represented byV= {v1,v2, . ..,vN}. Each element inVhas one-to-one correspondence to a component or subassembly of a product. The number of the subassemblies is represented byNinV. Components or subassemblies in a product are denoted by the nodes, while hyper-arcs represent disassembly tasks. A more complicated subassembly can be formed by two or more components or subassemblies to join together. The set of directed edges is represented byE= {eij}.A directed edge is represented byeij, representing a disassembly operation from nodevito nodevj. Notice that an AND relationship is that the two lines connect with an arc,and two lines must exist at the same time; an OR relationship is that a node has a variety of decomposition methods, and each decomposition method can independently exist.According to the above description of the diagram, a ballpoint link structure is constructed as shown in Figs. 5 and 6,respectively.

Fig. 5. Schematic diagram of a ballpoint.

An AND/OR graph is widely used to show all possible disassembly sequences of a product. It has been used in different applications, for example, the representation of satellite equipment for increasing the planning flexibility.

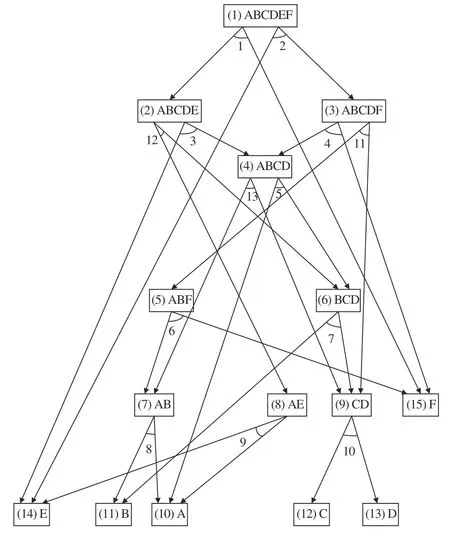
Fig. 6. The AND/OR diagram of a product.

Lambert [35] applied MP techniques for DSP with AND/OR graph representation. Minet al.[36] presented a weighted AND/OR graph to represent the product structure and element constraints for disassembly planning. Minet al.[37] proposed a method of dynamically calculating the weight value based on AND/OR graph to search the optimal disassembly sequence and discussed a problem with the uncertainty weight value of the directed edge.

Tsenget al. [38] proposed an AND/OR graph as a commonly-used representation approach for product disassembly studies. Nodes and hyper-arcs are adopted to construct it. The nodes denote subassemblies or components in a product, while the hyperarcs denote disassembly operations. Vigano and Gómez [39] used an AND/OR graph to represent the relationship among subassemblies/components of a product.

Kaiet al.[40] and Zhanget al.[33] developed an adjacent graph to represent connection relations among adjacent components as another visualized representation approach for DSP. Guoet al. [41] presented an AND/OR graph to represent product information for all disassembly sequences, and proposed a scatter search algorithm to optimize selective disassembly sequences subject to multiresource constraints to maximize disassembly profit. Note that selective disassembly aims to acquire a subset of components or subassemblies in an entire product via disassembly operations.

Renet al. investigated the disassembly planning considering sequence-dependent cost among disassembly operations by using an AND/OR graph. They proposed a mathematical model to maximize the recovery profit subject to sequencedependent cost. They also developed a novel two-phase heuristic method to effectively generate feasible disassembly sequences according to an AND/OR graph in reasonable computational time [42].

Theoretically, product information can be represented by an AND/OR graph for all disassembly sequences. However,when a product consists of a large number of components, a combination explosion problem is encountered and prevents engineers from performing efficient DSP.

C. Petri Net (PN) Modeling

PN represents the structure relation of a product or system for modelling. Zhaoet al. [31] proposed a disassembly PN(DPN) that consists of tokens, places, transitions and arcs with execution rules. A token represented the availability of a product, subassembly or component. Places denoted subassemblies or components or conditions of disassembly operations. Transitions correspond to actions, and arcs are similar to hyper-arcs in AND/OR graphs for disassembly routes. Many researchers have proposed the use of PNs for DSP. The PN representation is a popular tool in system modelling [43], [44]. It can address precedence relations among actions.

Therefore, PNs are extensively used in flexible manufacturing systems. A DPN of a product is established based on the concept of PN. A DPN of a ballpoint is shown in Fig 7.

Fig. 7. A DPN of a ballpoint.

Definition 1:A DPN is defined as a seven-tuple

DPN = (P,T,I,O,M,c,τ)

where

1)Pis a set of places.

2)Tis a set of transitions withP∩T=∅ andP∪T≠∅.

3)I:P×T→Nis an input function that defines a set of directed arcs fromPtoT.

4)O:O×T→Nis an output function that defines a set of directed arcs fromTtoP.

5)M:P→Nis a marking representing the number of tokens in each place. The initial marking is denoted byM0.

6)c:T→R+is a disassembly cost associated with a transition, whereR+is the set of non-negative integer numbers.

7)τ:P→R+is a recycling/reuse value associated with a place.

By using this method, a disassembly sequence is determined according to the cost and environmental benefits of a disassembly process, and the effectiveness and feasibility of the proposed method are illustrated by a real-life case study.In such a model, a place represents a component or subassembly, the position of a subassembly and fixed parts; a transition represents a disassembly task. Similar to a graphbased model, DPN becomes very complicated when the number of product components is large, and it is difficult to be automatically generated from product design information.Thus, resulting in high computational complexity to search the optimal disassembly plans. A number of researchers have adopted PNs to solve DSP:

Grochowski and Tang [45] pioneered in a hybrid Bayesian network and DPN to develop an expert system to determine the optimal disassembly action without human assistance. Kuo and Wang [32] applied DPNs for DSP of EOL electronic and electrical equipment. Giudice [46] adopted PNs to perform the automatic search process of the possible disassembly sequence for a robotic system.

Kuo [47] established a disassembly information model based on PN, and used the DPN analysis method to address the dismantling and recycling of discarded products. In order to combine PNs and meta-heuristic algorithms to solve DSP problems, Guoet al. [48] used PNs to represent discarded products and proposed an improved SS to optimize selective disassembly sequencing problem subject to multiresource constraints to maximize disassembly profit.

D. Matrix-based Modeling

The graph representations and component precedence relations are comparatively easy to understand by human experts. When a large-scale product has hundreds of components, with a complicated structure, it is difficult to draw manually product relationship diagram or an interpretative structural model. A constraint matrix is used to represent discarded products with a large number of components for automatic data processing, for instance the constraint matrices used for automatic disassembly planning.Generally, graph-based product descriptions have to be converted into matrix-based representations for computer processing.

However, all relationships of pairwise components are recorded by a matrix even if there is no constraint among components. The matrix-based format needs to reduce its size and processing time. In a mathematical model, indexidenotes a subassembly andjrepresents an operation. A sequence of operation indices represents disassembly sequences. The precedence relationship is represented by precedence matrixS= [sjk] between operations and operations in an AND/OR graph. InS, columnjand rowkdenote disassembly operation indices

Thus, precedence matrixSof a product as shown in Fig. 5 can be expressed as:

The connection relationships among all these operations should be met in a disassembly process. We can adopt a connection matrixC= [cjk] to describe them.

Thus, the connection matrix of a product as shown in Fig. 5 can be expressed as:

A constraint condition should be satisfied such that one subassembly cannot be obtained by multiple disassembly operations at the same time. For convenience, a disassembly matrixD= [dij] is used to define the relationship between subassemblies and operations. Indij,jandidenote disassembly operationjand subassemblyi, respectively.

Thus, disassembly matrixDof a discarded product as shown in Fig. 5 can be expressed as:

In order to present the geometrical and motion constraints between fasteners and components, Smith and Chen [49]adopted different matrix representations for fasteners,components, and constraints in computer recognizable formats for DSP. Smith and Chen [50] used four matrices:disassembly matrix and motion constraint matrix for components, disassembly matrix and motion constraint matrix for fasteners. A close relationship among product elements was included in an adjacent matrix. ElSayedet al. [51]developed matrix representations to store products’ structure information, components’ constraint relations as well as connections.Products’ geometrical constraints and connections are represented by matrices in DSP. Jiang and Wang [52]proposed a constraint matrix to store data of component constraints of disassembly operations in the format of a matrix.

E. Other Modeling Methods

In order to represent the different products, some researchers propose different modeling methods to solve DSP problems. For example, Wanget al. [53] used the disassembly feasible information graph to describe operation information and discarded product disassembly sequences. They transformed the problem of the DSP into a path search problem for searchable feasible information graph and proposed a genetic algorithm.

Liet al. [54] established the DSP model of discarded products to use the method of graph theory. The work [55]established a model of product disassembly and weighted mixed graph, which could effectively express the disassembly priority relationship among components and realized the optimal DSP of complex products by a particle swarm optimizer. The work [56] proposed a disassembly hybrid graph model to describe the structural connections among components and adopted a branch-and-bound algorithm to calculate the minimum work time of a disassembly sequence.

Penget al.[57] proposed different modeling methods for DSP for the efficient generation of disassembly sequences.Xinget al. [58] considered lot size disassembly and a reachability graph of parts and components and developed an integrated selection disassembly method to produce the best solution for product disassembly. ElSayedet al. [59] adopted a constraint exclusive method to generate a disassembly sequence. Then, the repetitive sequence was deleted by searching the target component. But they failed to give an optimization method to find target disassembly sequences.

Hanet al. [60] presented a disassembly precedence graph ofa used product and then proposed a new integer programming model for minimizing the total disassembly cost. Zhuet al.[61] introduced an efficient machine-readable disassembly information modeling method and linear program to find the optimal disassembly sequence. The information model adds dynamic capabilities to change the overall disassembly operation, which has been applied in the dismantling of mechanical products.

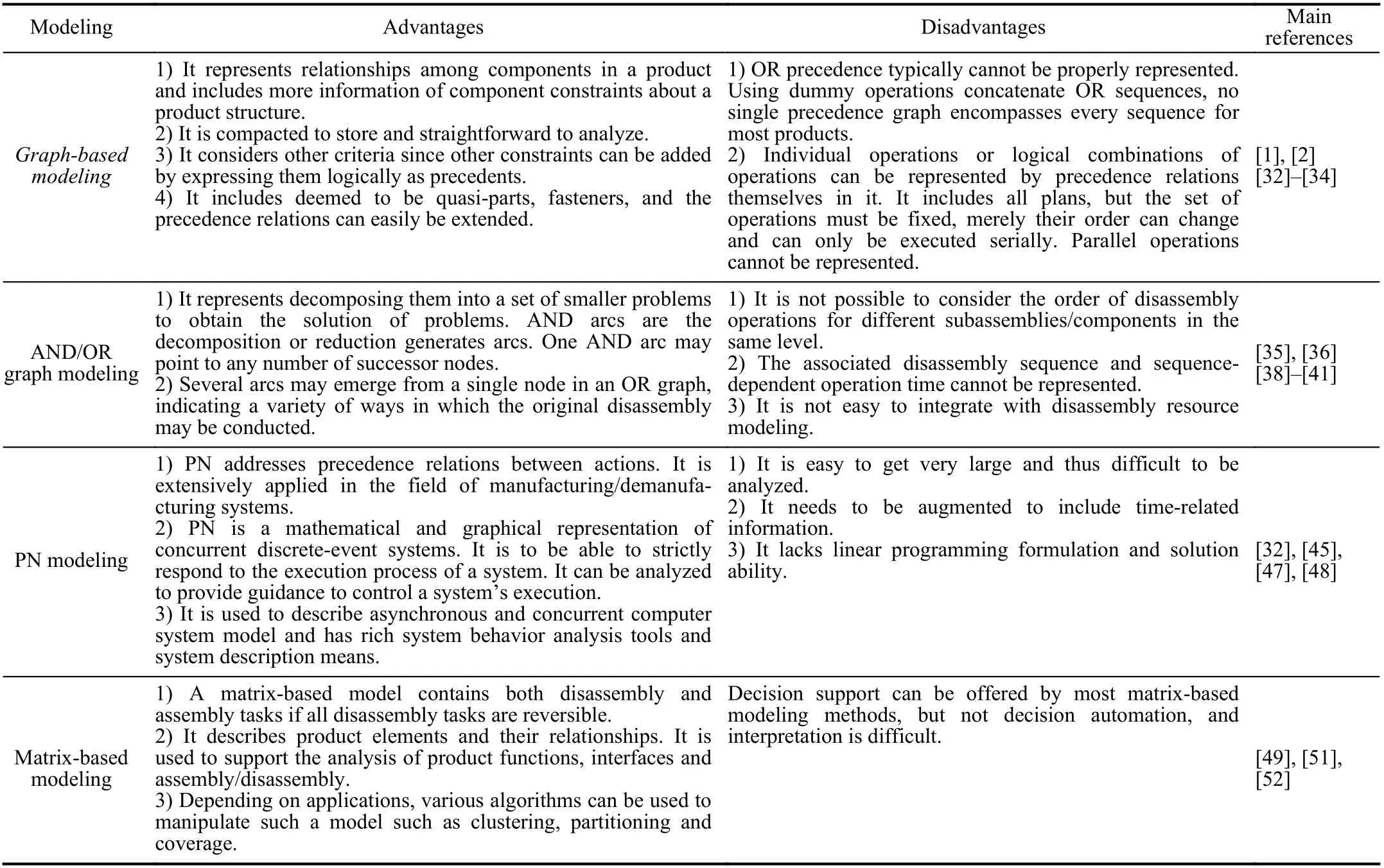
TABLE II COMPARISON OF MODELING METHOD FOR PRODUCTS TO BE DISASSEMBLED

Zhanget al. [62] adopted a fuzzy-rough set mapping model of parallel disassembly to generate the optimal parallel disassembly sequence. Mitrouchevet al. [63] used the lowest level of a product graph to generate the feasible disassembly sequence of selective disassembly.

III. MATHEMATICAL PROGRAMMING METHODS

Mathematical programming (MP) is used to select the best one from a set of available alternatives. A functionf:A→R is given from some setAto the set of real numbers, findx* ∈Asuch thatf(x*) ≤f(x) for allx∈A(“minimization”) or such thatf(x*) ≥f(x) for allx∈A(“maximization”). Such a formulation is defined as an MP problem or an optimization problem. MP techniques are used to make variables (solutions) efficiently converge to the optimal one without the need of visiting a whole solution space. In a disassembly case, a DSP optimization problem consists of maximizing profit and/or minimizing energy by systematically choosing input values from an allowed set and computing the value of the objective functions. An area of applied mathematics is constituted by the generalization of optimization theory and techniques to other formulations. Generally, DSP aims to find the optimal disassembly sequences given some objective functions and a domain. Different domains and objective functions are often involved.

In DSP, MP methods require modelling with a high level of abstraction. The problem description is started from assembly drawing or a CAD-file. Then a connection diagram and a set of precedence relations are derived. This needs dedicated software or visual inspection. Formalizing a DSP problem implies the determination of its decision variables, data variables, constraints and objective functions. Optimal and sub-optimal disassembly sequences can be obtained after disassembly cost is assigned to every disassembly operation,and revenues of the components are assigned to every subassembly/component. The proper modelling of a DSP is the prerequisite for an MP method. Once modelled, MP methods are available for selecting optimal disassembly sequence. These MP methods include linear programming,mixed integer programming, and dynamic linear programming. The mathematical models for DSP can be easily modified and often need virtually negligible execution time if problem size is small, These MP methods need a strictly formal mathematical model as a prerequisite. MP is not appropriate for investigations because it requires many detailed studies in disassembly method design and product design. Even in those cases, the application of MP is useful in an exploratory study. It has to be carried out before more detailed observation. The flowchart of using MP is shown in Fig. 8.

Fig. 8. The flowchart of MP.

The particular characteristic of MP is that the optimal solution to a model can be obtained automatically by some commercially available optimizer. An MP model answers the question “What’s the best?” rather than “What happens?”. MP is more restrictive than other techniques. A model with too many constraints and decision variables may lead to no or low-quality solution given limited computation time. If a model is well-built, its solution can be used for a real-world problem.

Some DSP methods use MP techniques to get optimal disassembly sequences that maximize revenue. For instance,Tripathiet al. [64] proposed a fuzzy disassembly optimization model with its aims at determining the optimal disassembly sequence and the optimal depth of disassembly to maximize the net revenue at the EOL disposal of a product. An innovative self-guided ant algorithm was proposed to deal with the computational complexity of DSP. Its performance under various factors was tested on a set of test instances. It consumed many computing resources.

Lambert and Gupta [65] developed a heuristic algorithm to detect “ good enough” solutions for DSP in the case of sequence-dependent costs. Heuristic and iterative binary integer linear programming methods were implemented on a cellphone that consisted of 25 components. This method cannot solve a large-scale product disassembly problem.

Maet al.[66 ] used integer programming techniques to address the three decision variables in a parallel disassembly environment for maximizing profit. A two-phase algorithm was proposed to solve a DSP problem. To show its effectiveness, an automatic pencil and a telephone were used to test the proposed algorithm. Test experimental results on other general product structures were reported.

Zhuet al. [61] introduced an efficient and machine reachable disassembly information model and presented a linear programming-based optimization model to obtain the optimal disassembly sequence. The model added dynamic capabilities to handle state-dependent information such as parts’ disassembly directions which may change after a disassembly operation. An electrical–mechanical device was used to test the proposed method. Its application is limited.

Behdadet al. [67] proposed an immersive computing technology to solve a stochastic mixed-integer nonlinear program incorporating data collected to determine an optimum disassembly sequence. Then, they applied immersive computing technology to explore initial solutions. Finally,they modified product design by combining the results of both mathematical model and immersive computing technology simulation. They used a Burr puzzle to show their method’s application. The problem with their method is that the amount of data is too large, and the calculation is too tedious. Kimet al. [68] proposed to minimize the sum of operation and sequence-dependent set-up costs in DSP. An integer program was proposed. An extended process graph was used to represent all possible disassembly sequences, and then optimal solutions were found by a branch and bound algorithm. The lower and upper bounds were obtained by incorporating the methods as well as a dominance property to reduce search space. There are too many parts for calculation. The deficiency is that it is easy to make some calculation error. Luet al. [69] studied mathematical programming, designed an exact approach to produce optimal solutions. This method has difficulty to deal with large-size products.

IV. INTELLIGENT OPTIMIZATION

To solve a DSP problem, many studies have investigated intelligent optimization algorithms. The objective of an intelligence algorithm is to produce a high-quality solution in a reasonable time. It may simply approximate the exact solution, but it is still valuable because finding it does not require a prohibitively long time. This solution may not be the optimal solution to this problem. An intelligent algorithm is an algorithm that uses some heuristic strategies and does not guarantee to find the optimal solution.

Both complete and selective disassembly planning methods for a product are often needed and always based on some,product representation models and plan approaches. For example, Aguinagaet al. [70] used rapidly growing random tree-based algorithm; Adenso-Díazet al. [71] adopted a heuristic approach; and Tianet al. [72] adopted neural networks. Liuet al. [73] adopted an improved max–min ant system; while Yeh [74] proposed a self-adaptive simplified swarm optimization method. Different approaches and algorithms can be employed for solving DSP, which include machine learning, reinforcement learning, neural network,intelligent perception with the Internet of Things, and cloud computing/edge computing.

We classify DSP problems into single-objective and multiobjective ones that can be well solved via intelligent optimization algorithms. Their comparison is given in Table III.

A. Single-objective DSP

Single-objective DSP problems are paid more attention by researchers in recent years. Their solutions are reviewed as follows.

1) Genetic Algorithms (GA) and Related Solutions:Shimizuet al. [75] applied GA as a solution method to obtain an optimal disassembly sequence. Xieet al.[27] developed a hybrid of GA and the simulated annealing method to prevent GA premature convergence problem when solving a DSP problem. The method is efficient and feasible to search the optimal or near-optimal disassembly sequence in solving computational problems. Giudice and Fargione [76], and Duţǎet al. [77] presented GA-based methods to find disassembly sequencing of EOL products. Wanget al. [78] provided a disassembly feasibility information graph to describe the structure of a discarded product. According to such a graph,GA is used to quickly find optimal solutions while minimizing disassembly cost. Mohantaet al. [79] proposed GA and its combination with other search strategies to improve GA’s performance. Goet al. [80] presented an optimization model for DSP and solved it by using GA. An objective function of GA is dependent on the increment in disassembly time in [80].Smith and Hung [81] used modular design theory and recursive rules to generate disassembly sequences. Then GA was used to search optimized parallel disassembly sequences in which the feasibility and effectiveness of solutions can be guaranteed according to the use of recursive rules. Khederet al. [82] considered the maintenance of used components,disassembly directions, the effect of changing tools, and volume of parts, and designed an objective function with different weights. They adopted a precedence preservative crossover in GA, which feasibility and effectiveness of the obtained disassembly sequences after a crossover process.Alshibliet al. [83] improved GA for DSP by using a faster metaheuristic algorithm, i.e., Tabu search, to get the suboptimal solution. Tsenget al.[84] and Kongaret al.[85]proposed an improved block-based GA for DSP. Renet al.[86] proposed an asynchronous parallel DSP problem that posed no synchronization requirement and a GA-based solution algorithm to solve it.

2) Ant Colony Optimizer (ACO):McGovern and Gupta [13]presented ACO to deal with a DSP problem. Tripathiet al.[64] presented a fuzzy DSP problem formulation method by using the uncertainty inherent in quality of discarded products.They proposed an ACO-based metaheuristic algorithm to determine the optimal disassembly sequence as well as the optimal depth of disassembly. Malik [87] developed ACO to mimic ants’ behavior. For DSP, if a component in a disassembly sequence cannot be disassembled, this disassembly sequence would be marked as an infeasible sequence. It was then not necessary to consider the following components in this disassembly sequence. Based on ACO,Wanget al. [88] solved the DSP problem of an automotive engine, which consisted of 50 components after the simplification. Eldoset al. [89] presented the positive feedbacks that led to all ants in the trail. Luoet al. [90] used ACO to select the near-optimal solutions and applied it to industrial applications in order to generate the multi-layer product representation.

3) Particle Swarm Optimizer (PSO):Studies [91], [92] used PSO to solve a DSP problem. Yeh [93] proposed an improved simplified swarm optimization algorithm for the update mechanism to adjust the self-adaptive parameter control procedure for DSP.

4) Scatter Search (SS):Liet al.[94] developed SS as a swarm optimization algorithm to solve a selective DSP problem. Guoet al.[48] adopted SS to solve DSP problems and obtain sub-optimal solutions.

5) Artificial Bee Colony Algorithm (ABC):Percocoet al.[95] adopted an ABC algorithm to deal with a multi-objective DSP, while they simplified multiple objectives DSP in to a weighted sum expression, thus resulting in a single-objective DSP problem. Liuet al. [96] developed an improved discrete ABC to address a robotic DSP problem to minimize total disassembly time. Liuet al. [97] proposed a modified ABC to conduct the collaborative optimization of robotic DSP and robotic disassembly line balancing.

6) Other intelligent optimization methods:Reveliotis [26]proposed a reinforcement-learning-based method to compute near-optimal solutions. Alshibliet al. [83] presented a tabu search (TS) algorithm to address a selective DSP problem.Taoet al. [98] proposed a TS-based hyper heuristic algorithm with an exponentially decreasing diversity management strategy. Compared with the low-level heuristic algorithm,their proposed TS-based hyper heuristic algorithm is more efficient in terms of exploration ability and improving energy benefits. Smithet al. [49] developed a rule-based recursive selective disassembly method to obtain a near-optimal solution of discarded products, and used five disassembly rules to define the disassembly order or precedence relations among components.

B. Multiple-objective DSP

Multi-objective optimization is applied in the field of DSP where the optimal decisions need to be taken in the presence of trade-offs between two or more conflicting objectives. In practical DSP problems, there may be more than two objectives. Many disassembly problems involve multiple objectives that are not describable as the-more-the-better or the-less-the-better ones. Instead, there is an ideal value for each objective, and the desire is to get as close as possible to the goal value of each objective. For example, in an actual disassembly process, the use of advanced tools and skilled workers can reduce disassembly time while perhaps increasing disassembly cost. Thus, disassembly sequences have a trade-off between cost and time or energy and cost.

There is a traditional method in solving a multi-objective DSP problem. Based on the relative degree of importance of each objective, it uses different weights for different objectives and then sum them into a single objective function,thus resulting in a single-objective DSP problem. However,this method is not ideal to solve a multi-objective DSP problem. Since DSP involves different decision-makers with different legislative and economic considerations, one singleobjective solution cannot meet the needs of different decisionmakers. Furthermore, it makes sense that as many nondominated solutions as possible should be selected for a decision-maker in order to make better decisions. Multiobjective evolutionary algorithms have been widely studied and applied to solve multi-objective problems. For example,Debet al. [99] proposed a non-dominated sorting genetic algorithm II (NSGA-II). Kongar and Gupta [85] considered three objectives, i.e., disassembly directions, demand, and methods, to present a weighted multi-objective GA to solve a disassembly problem. Zhang and Li [100] presented a multiobjective evolutionary algorithm based on a decomposition procedure to solve a DSP problem.

Aguinagaet al.[70] developed an improved rapid growing random tree-based algorithm that solved a disassembly path planning problem. Two objective functions were used to evaluate a given disassembly sequence. The first one provided the cost of traversing the graph from the initial configuration.The second one offered a heuristic value of the cost from a given position to the goal.

Adenso-Díazet al. [71] developed a particular bi-criteria DSP problem to fulfill two objectives, where one was to minimize the cost of disassembly by keeping it close to a predefined aspiration level, and another was to disassemble components according to a priority list. They proposed to use a greedy randomized adaptive search procedure and a pathrelinking-based heuristic methodology to solve it. Aliet al.[101] developed a multi-objective differential evolution algorithm to deal with a similar DSP problem.

Rickli and Camelio [102] used a multi-objective GA to solve a selective DSP problem. Renet al.[103] developed a multi-objective discrete ABC to minimize disassembly time and maximize profit. They compared it with NSGA-II [99] in GA, and demonstrated that it outperforrmed NSGA-II with their obtained the experimental results.

Guoet al. [104] developed a multi-objective SS algorithm to deal with a selective DSP problem, which involved the determination of optimal disassembly sequences for single or multiple target components. Guoet al. [105] proposed lexicographic multiobjective SS to address the proposed multiobjective optimization problem. Their experimental results verified that it provided a better solution in a short execution time and fulfilled the precedence requirement in a product structure and resource constraints. Guoet al. [41] proposed an SS algorithm to solve the dual-objective optimization model for selective DSP subject to the multi-resource constraints such that disassembly profit was maximized and disassembly time was minimized. Its effectiveness and feasibility were verified by comparing its optimization results with those of genetic local search. Guoet al.[106] developed a multiobjective GA based on an external archive to minimize disassembly energy and maximize profit. By comparing it with NSGA-II , they demonstrated that its optimization results were better than NSGA-II’s.

V. DSP CONSIDERING UNCERTAINTY

Since the quality of EOL products is usually different,disassembly time, cost and energy should be described as a random variable instead of deterministic ones as assumed in most existing DSP studies. Therefore, a stochastic DSP model should be established where the uncertainty of various variables is introduced. The resulting DSP problems require much more efforts to solve.

There is a widely used technique called Monte Carlo simulation, which handles various distributions of uncertain and random variables and correlations among input factors for a stochastic DSP model. In this technique, each parameter follows a distribution function. Then each distribution function generates data as input for a DSP model to produce output results. As shown in Fig. 9, a Monte Carlo simulation takes each uncertain variable and assigns it a random value.We then run a model to obtain a result. We repeat this process for multiple times and finally use the averaged result as a needed estimate.

Fig. 9. Uncertainty analysis.

Disassembly of EOL products is a process in which uncertainty usually happens. Such products consist of a mix of different configurations, types, materials and even brands of products. The exact data might be partly lost on the component’s weight information and material composition.Data on the quality of definite modules is difficult to get it during a disassembly process, which influences further decisions on a disassembly sequence and depth. Uncertaintyhandling methods are thus developed to solve a DSP problem reasonably due to the presence of a corrupted subassembly or component. Since EOL products have been used for a certain period of time, many uncertainties may be encountered in their disassembly process. For example, the condition of a used product is uncertain due to unknown environmental factors and human behavior during its used stage. In addition,when an EOL product is disassembled, disassembly process factors, such as the operational fluency of a disassembly worker and the choice of removal tools and methods affect its disassembly results. Thus, some uncertainty management problems and the DSP problem with uncertainty parameters need to be addressed.

Most of the existing studies in DSP with uncertainty deal with such uncertainty of characteristics as component recovery cost, the value of recovered components, component recovery rate and quality [2], [64], [107]–[109]. Reveliotis[26] performed the uncertainty management through learningbased strategies in the optimal DSP problem.

Tang [110] pioneered a learning-based disassembly process planner. She considered the expected disassembly cost and expected net profit of the EOL product disassembly based on a generic model for a human-the-loop disassembly system and analyzed the uncertainty feature of disassembly time and quality of disassembled subassemblies in a disassembly process. She solved the DSP problem by proposing a machine learning approach based on a DPN and a hybrid Bayesiannetwork.

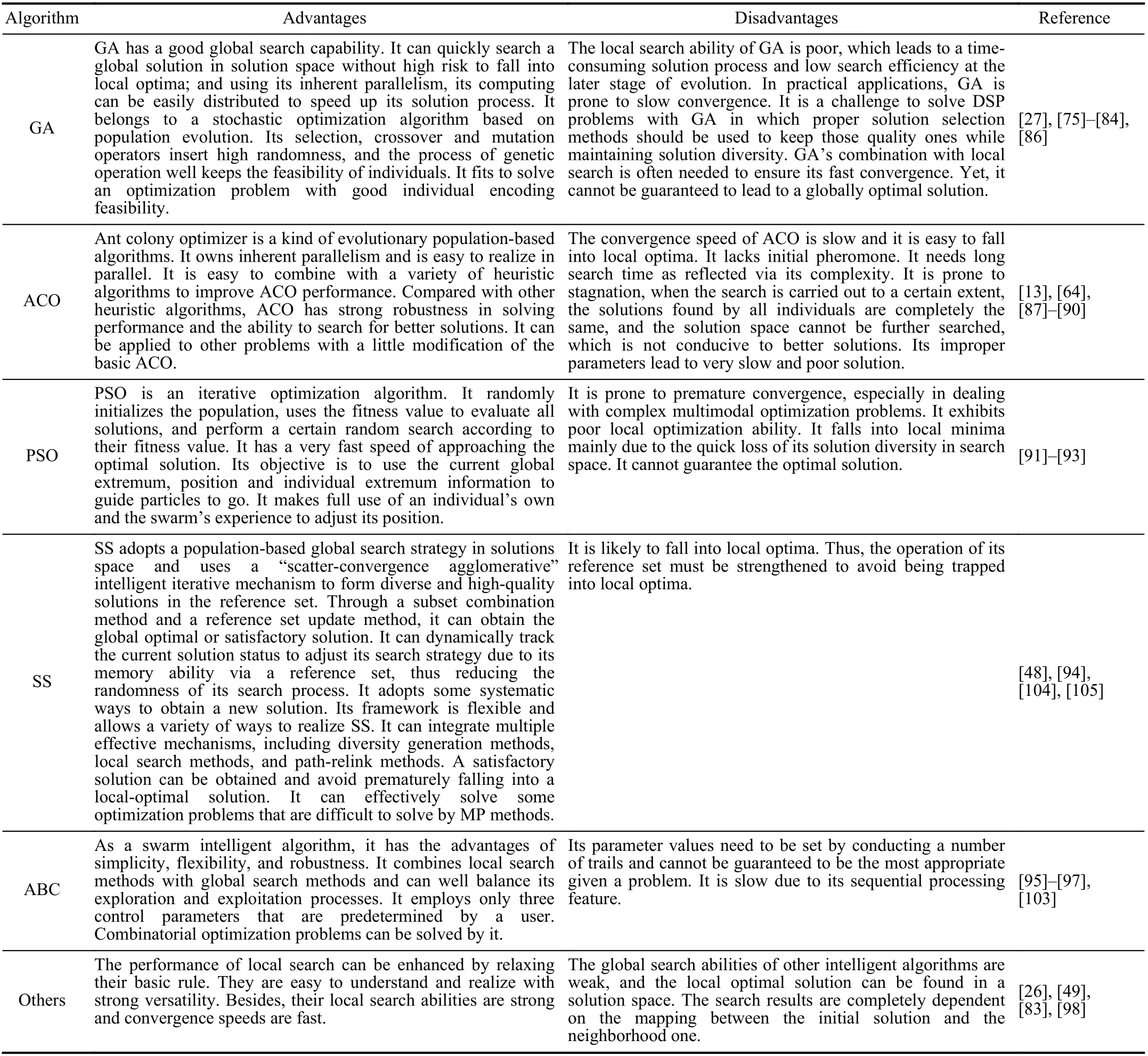
TABLE III COMPARISON OF INTELLIGENT OPTIMIZATION ALGORITHM

Tripathiet al.[64] considered the uncertainty inherent in the quality of discarded products in a fuzzy DSP problem. Behdad and Thurston [1] dealt with the probability of damage during disassembly, component repair or replacement, and reassembly process. They considered both disassembly and reassembly costs and uncertainties, and presented a method for addressing their tradeoffs, as well as the uncertainty associated with them. Ilgin and Gupta [9] described a methodology for DSP for products with defective parts. They presented the uncertainty-related difficulties in DSP.

Behdadet al.[67], [111] presented a new procedure for DSP with uncertainty. By considering uncertain disassembly process outcomes such as time, cost, and the probability of incurring damage, they determined the best sequence for product disassembly. Tianet al.[112], [113] considered an energy management method for DSP integrating stochastic simulation and the maximum entropy principle. Behdad and Thurston [2] proposed the uncertainty sources that were different depending on the purpose of disassembly.Uncertainty in the incoming feedstock design, material, age,and quantity creates enormous impediments to cost-effective operations when component reusing, remanufacturing or recycling is performed. Uncertainty lies in dimensional instability and the possibility of causing damage to valuable components when disassembly is for product maintenance.Tianet al.[114], [115] analyzed the main uncertainty factors for a disassembly process and perform the evaluation of their impact on the process. A chance-constrained programming approach was proposed to determine the optimal disassembly sequence. Ullerich and Buscher [30] presented a flexible DSP problem and its solution method by considering product conditions. In addition, Tianet al. [116], [117] developed a chance-constrained simulation process based on a neural network and GA. They considered random, disassembly time and cost.

Bentahaet al.[19 ] considered selective disassembly to solve a stochastic disassembly line balancing problem to obtain a disassembly sequence. Maximizing profit is the objective function given stochatic task execution time. Rickli and Camelio [118] considered the uncertainty about quality of an EOL product and developed an approach for selective disassembly sequence generation. Zhouet al. [119] developed a time window-based preventive maintenance model for multi-component systems with the consideration of stochastic failures and disassembly sequences. They adopted a Monte-Carlo based algorithm to simulate the stochastic failures and calculate the cumulative maintenance cost of the system.

VI. CONCLUSIONS AND FUTURE RESEARCH

Covering the field of DSP, this review paper is organized according to the DSP modeling and solution methods [120]–[128]. The following conclusions can be drawn from our literature review and survey:

The use of graph-based models, AND/OR graphs, Petri nets,and matrix models has been described to be promising to conduct DSP [129]. They have some limitations such as inability to handle the order of disassembly actions in the case of parallel disassembly.

The use of AI techniques is an increasing trend. They include fuzzy systems, metaheuristics, and neural networks(Garibaldi [130], Ghahramani [131]). The combinatorial explosion problem that would be encountered with MP approaches can be avoided at the expense of no guaranteed optimality of an obtained solution. The use of AI techniques can help us narrow down the solution search space, thereby reducing the computational cost. Once the number of reasonable possibilities is greatly reduced, intelligent optimization algorithms can help engineers find desired and sometimes optimal solutions fast.

DSP problems face a high degree of uncertainty. A simulation method is the most popular one to deal with such uncertainty. Stochastic programming, robust optimization, and sensitivity and scenario analysis can be employed. Some research efforts are needed to control the effects of uncertainties. A variety of uncertainty-handling approaches are adopted in the literature to solve the practical problems.Some of them have been reviewed in this paper. They can reduce the search space for DSP.

Today, disassembly sequencing is mainly applied to the biochemistry area as shown in Fig. 10. The main reason is the increasing attention of governments, firms, and academicians toward environmental issues, for instance, reducing or eliminating environmental pollution, decreasing the usage of natural resources and preventing global warming. In this developmental period, some researchers mainly focus on tactical issues and operations to satisfy the immediate needs of industrial firms and governments. Some strategic models should be developed for the analysis of disassembly systems in terms of organizational dynamics and technological advances.

Fig. 10. Percentages of publications based on the application of DSP.

Advanced DSP techniques are expected to become highly cost-effective in realizing product reuse and recovery to handle high penalty cost and strict regulations associated with the use of virgin material resources and waste management. It is increasingly important to design efficient disassembly lines,and solve planning and scheduling problems to automate and optimize a product recovery process [132]. Furthermore, we should investigate the issues arising from a disassembly line’s design and operations. We have to address the challenges in workload balancing among its workstations and introduce machine learning and AI approaches to provide fast and desired solutions to nonlinear and multi-objective disassembly line balancing, planning and scheduling problems. Besides,such problems subject to multi-resources constraints and reverse logistics require much research.

Remanufacturing industry needs to focus on the integration and applications of digitalization, networking and AI to various sectors:

1) Home and Industrial Appliances:They include all electronic products that have varying usage time with some being rather short, e.g., cell phones; while others being long,e.g., microwave ovens. These electronic products’ parts have the relatively complex structures, irregular shape,metallurgical combination and good fatigue resistance.Intelligent disassembly technology can be used to effectively improve the accuracy of their cladding dimension and performance of their cladding parts. It plays a critical role in supporting the development of national circular economy,realizing energy conservation and greenhouse gas emission reduction, and coping with global climate change.

2) Aerospace:In this sector, core parts such as aeroengine blades should be remanufactured on a large scale. The quality of remanufactured aeroengine blades has to be equivalent to that of original/new products through professional repair or upgrading. Besides they have small damage over tolerance and high requirements for fit. Intelligent inspection,disassembly and remanufacturing technologies are required.

3) Medical and Health Care:The remanufacturing of key parts of high-end medical instruments and image acquisition equipment needs more progresses. These products’ parts have complicated structures and various shapes, and heavy load parts with a metallurgical combination. Internet of Things,cloud computing and big data, intelligent disassembly technology can provide customers with fast and efficient solutions, improve the remanufacturing rate of high-end medical instruments, and maximize product benefits.

4) Battery and Energy Products:Their use has been increasing as more and more electric devices become wireless/portable and numerous electric vehicles are put into use. These products’ parts have a regular shape, relatively simple/standard structures, large corrosion and wear tolerance,and high repair efficiency requirements. The intelligent disassembly and recovery can effectively shorten the remanufacturing cycle of retired battery products, improve production efficiency, reduce resource and energy consumption and protect our environment through greenhouse gas emission reduction.

For the development of intelligent disassembly technologies, it is necessary to continuously carry out research along the direction of Industry 4.0, AI, big data processing, machine learning and intelligent perception with the Internet of Things.It is required to deeply integrate the Internet of Things, cloud computing/edge computing, and AI technologies [130]–[137]into intelligent disassembly/remanufacturing systems and promote remanufacturing industry in various industrial sectors.