Lightweight Image Super-Resolution via Weighted Multi-Scale Residual Network

2021-06-18LongSunZhenbingLiuXiyanSunLichengLiuRushiLanandXiaonanLuo

IEEE/CAA Journal of Automatica Sinica 2021年7期

Long Sun, Zhenbing Liu, Xiyan Sun, Licheng Liu, Rushi Lan, and Xiaonan Luo

I. INTRODUCTION

IMAGE super-resolution (SR), which is to recover a visually high-resolution (HR) image from its low-resolution (LR)input, is a classical and fundamental problem in the low level vision. SR algorithms are widely used in many practical applications, like computational photography [1], scene classification [2], and object recognition [3], [4]. The SR technology can be roughly divided into two categories based on the number of input frames: multi-frame super-resolution[1], [5], [6] or single image super-resolution (SISR) [7]–[9]. In this work, we focus on SISR.

Although numerous approaches have been proposed for image SR from both interpolation [10] and learning perspectives [7], [11]–[13], it is still a challenging task due to that multiple HR images can map to the same degraded observation LR. Recently, with the powerful feature representation capability, deep learning-based models have achieved superior performance in the low-level vision tasks,such as image denoising [14], [15], image deblurring [16],image deraining [17], image colorization [18] and image super-resolution [8], [19]–[28]. These methods learn a nonlinear mapping from degraded LR input to its corresponding visually pleasing output.

Observing the advanced SISR algorithms shows a general trend that most existing convolutional neural network (CNN)-based SISR networks highly rely on increasing model depth to enhance the reconstruction performance. However, these methods would rarely deploy to solve practical problems because many devices certainly cannot provide enough computing resources. Therefore, it is crucial to design a fast and lightweight architecture to mitigate this problem [29].

To build an efficient network, we propose a weighted multiscale residual network (WMRN) (Fig. 1) for SISR in this work. Specifically, instead of using conventional convolution operation, we first introduce depthwise separable convolutions(DS Convs) to reduce the number of model parameters and computational complexity (i.e., Multi-Adds). For exploiting and enriching multi-scale representations, we then conduct weighted multi-scale blocks (WMRBs), which adaptively filter information from different scales. By stacking several WMRBs, the representation capability can be improved.Moreover, global residual learning is adopted to add highfrequency details for reconstructing better visual results. The comparative results indicate that WMRN achieves state-ofthe-art performance via a high efficiency and a small model size.

In summary, the main contributions of this work include:

1) A novel weighted multi-scale residual block (WMRB) is proposed, which can not only effectively exploit multi-scale features but also dramatically reduce the computational burden.

2) A global residual shortcut is deployed, which adds highfrequency features to generate more clear details and promote gradient information propagation.

3) Extensive experiments show that the WMRN model utilizes only a modest number of parameters and operations to achieve competitive SR performance on different benchmarks with different upscaling factors (see Fig. 2 and Table I).

The rest of this paper is organized as follows: Section II presents a brief review of the related works, Section III details the proposed method and Section IV evaluates the proposed algorithm from different aspects. Section V finally draws the conclusions.

Fig. 2. Multi-Adds vs. peak signal-to-noise ratio (PSNR). The PSNR values are evaluated on the B100 dataset for ×2 SR. The Multi-Adds are calculated by assuming that the spatial resolution of output image is 720 P. The proposed WMRN strides a balance between reconstruction accuracy and computational operations.

II. RELATED WORKS

A. Deep Architecture for Super-Resolution

Since Donget al.[19], [30] first introduced a CNN-based method (named SRCNN) to SR task, a series of deep learningbased works [8], [20]–[27], [31] have demonstrated impressive performance by jointly optimizing the feature extraction,nonlinear mapping, and image reconstruction stages in an endto-end manner in the recent years [31].

With regard to SRCNN, it was a three Conv layers network and achieved superior performance against the conventional example-based or reconstruction-based methods. Later, to ease the training difficulty from plain architecture, Kimet al.[20] employed global residual learning strategy to build a very deep super-resolution (VDSR) framework and showed a significant improvement over the SRCNN model. The following works like DRCN [21], DRRN [22] and MemNet[32] also adopted similar manner to improve the final results.Although the above methods obtained good performance, they all operated on the bicubic-interpolated HR space, which relatively added computational budget along with artifacts.

To reduce the computational cost caused by pre-processed input, FSRCNN [33], and ESPCN [23] directly extracted features in the LR space and adopted an upscaling layer in the final upsampling phase to reconstruct images. Nevertheless,they explored two different upsampling ways: transposed convolutional layer [34] and sub-pixel convolution (i.e., pixel shuffling). As a trade-off of speed, both FSRCNN [33] and ESPCN [23] have limited the model size of networks for learning complex nonlinear mappings [35]. Furthermore, the VDSR method [20] also proved that building a deeper network with residual learning could achieve better reconstruction performance. After that, an increasing number of works focused on designing more complex CNN architectures to improve performance. Limet al.[8] proposed a wide residual network (EDSR) and a multi-scale deep model(MDSR) for enhancing SR performance and made a significant improvement. Zhanget al.[36] combined residual learning and channel attention mechanism to build the SR model with the largest depth (more than 400 layers) and achieved great improvement in terms of PSNR.

Although various techniques have been proposed for SISR,most existing CNN-based models increase the reconstruction performance by increasing model complexity with a deeper network and neglecting their higher inference time and computational burden; this limits their applications in real-life.As a result, it is desirable to design a lightweight framework with a considerable performance for the SISR problem. We attempt to explore an available solution in this paper for the purpose.

Recently, there has been a rising interest in building lightweight and efficient neural networks for solving the SISRproblem [9], [25], [26], [29], [37]. The CARN model utilized a cascading mechanism upon a residual network for efficient SR and achieved competitive results. Huiet al.[37] proposed a information distillation network to gradually extract features for the reconstruction of HR images. Wanget al.[9]introduced an adaptive weighted residual unit for fusing multiscale features and obtained better reconstruction performance.Unlike they only used the multi-scale scheme in the upsampling part, we carefully designed a multi-scale module based on dilated convolution, which was stacked as a backbone network for effective and efficient feature extraction.

TABLE I PUBLIC BENCHMARK RESULTS. AVERAGE PSNR/SSIM VALUES FOR MAGNIFICATION FACTOR ×2, ×3 AND ×4 ON DATASETS SET5 [53],SET14 [54], B100 [55], URBAN100 [13], MANGA109 [56]

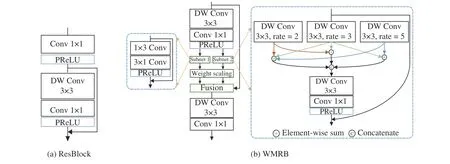
Fig. 3. The proposed building block. From left to right are: (a) ResBlock that used for extracting shallow feature; (b) WMRB, the core module of our model,generats the weighted multi-scale representations.

B. Loss Functions for Super-Resolution

Loss functions are generally used to measure the difference between super-resolved HR outputs and referenced HR images, and guide the model optimization [38]. ℓ1and ℓ2are the most widely used loss functions in SR field. Researchers tented to employ the ℓ2loss in early times, but later empirically found that ℓ1loss could achieve better performance and faster convergence [8], [37]. While obtaining high PSNR values, the HR image processed with the above functions often lack high-frequency details and produce overly smooth textures [39].

For improving perceptual quality, the content loss [39], [40]is introduced into super-resolution to generate more visually perceptible results. The generative adversarial network-based(GAN-based) SR algorithms are usually trained with content loss and adversarial loss [39], [41] to create more realistic details. As so far, however, the training process of GAN is still unstable.

In this work, we introduce total variation penalty ℓTV[14],[25], [42] to constrain the smoothness of ℓ1-processed HR images. From the experimental results (see Fig. 1), the linear combination of ℓ1and ℓTVgains a tradeoff between visual quality and PSNR values.

III. METHOD

In this section, we introduce the proposed weighted multiscale residual network (WMRN) in detail. An overall framework description is first given, and then the main building block of WMRN is also introduced. The training strategy is shown at the end of this section.

A. Network Structure

The goal of SISR is to estimate the high-resolution imageIS Rfrom the given low-resolution counterpartILR. As shown in Fig. 1, the proposed approach can be divided into three components: feature extraction (FE), nonlinear mapping(NLM), and image reconstruction.

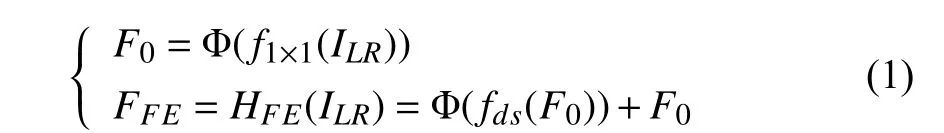
Specifically, we utilize a residual block (ResBlock) (see Fig. 3(a)) to extract low-level feature information. To express formally, let us denotefas a Conv layer (e.g.,fdsrefer to depthwise separable convolution operator, to be described in the next section) and Φ as an activation function. Then, theFEprocedure can be formulated as whereHFErepresents the feature extraction function, andF0is an output of the first convolution in ResBlock andFFEdenotes the feature maps from FE module. Then,FFEis sent to the nonlinear mapping (NLM) module that contains several WMRBs. For improving the high frequency details ofIS R, we additionally employ global residual learning. This can be defined as

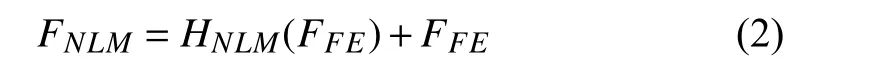
whereHNLMis the function of nonlinear mapping, to be discussed in detail in Section III-C.FNLMdenotes the generated deep intermediate features. Finally, an image recovery subnet is adopted to handle the feature maps after applying FE and NLM functions, which aims to recover the HR imageIS R:

whereHRECis the reconstruction module,fHRrepresents the last convolution function working on HR space,fUPcorresponds to the upsampling module andfRECdenotes a Conv layer in reconstruction subnet.

B. Depthwise Separable Convolution

To improve efficiency, we need to balance the relationship among parameters, Multi-Adds, and performance. Thus,parameter-efficient operations are introduced to achieve this purpose. In this work, depthwise separable convolution (DS Conv) [43]–[46], constructed by a depthwise convolution(DW Conv), i.e., a single spatial filter performs on per input channel, and a pointwise layer (i.e., 1×1 convolution exploits linear combinations over the intermediate features), is highly applied.

Let κ be the convolutional kernel size.cinandcout,respectively, denote the numbers of input and output channels of the tensor, andh×wrepresents the size of feature map. The computational cost of a standard convolutional layer is ash·w·cin·cout·κ·κ, while the costCDSof DS Conv is given by

By replacing regular convolutional operation, we can reduce the computation by the ratioRof

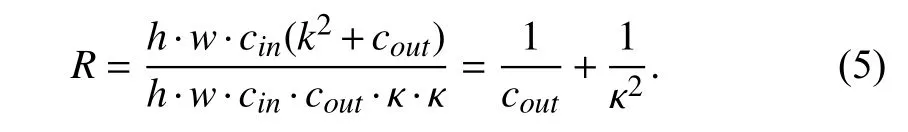
Unlike the original DS Conv utilized in [46], we use a dilated depthwise convolution in this work. It can enlarge the receptive field without introducing additional computing budgets.

C. Weighted Multi-Scale Residual Block (WMRB)

The overall structure of WMRB is shown in Fig. 3(b). It mainly includes three parts: extracting multi-scale features,weighting feature representations, fusing hierarchical information.

The multi-scale representations correspond to a number of feature maps obtained under multiple available receptive fields. To exploit different feature scales, we firstly employ a DS Conv to process the input tensor τiand then further adopt two parallel subnets. Specifically, the left module introduces two asymmetric convolutions [43] to utilize vertical and horizontal orientation features and fuse the output with previous input data via residual connection within this block.Let τi+1be the output of the first DS Conv, this procedure can be formulated as

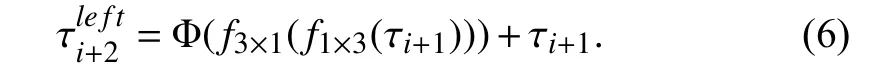
For enlarging the receptive field, we apply several dilated DS Convs with different rates on the right branch. Inspired by[25], [43], [44], [47], [48], to avoid the gridding effect caused by dilated filtering [15], [47], [49], we fuse these multi-scale information in the fashion of element-wise sum and then concatenate them for subsequent processing. Similarly, we also use a shortcut connection to preserve previous features and propagate gradient information. The mathematical expressioncanbewrittenas

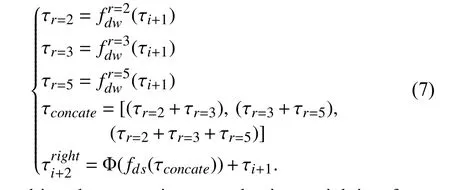
After multi-scale processing, an adaptive weighting factor set (α1,α2) is employed to scale the intermediate results, and then we fuse these weighted features and the original input tensor in a manner of pointwise addition. The initial value of the weight factors are set to 0.5 in this work. Lastly, a DS Conv is conducted for further filtering:

D. Loss Function

For training the proposed CNN model, rather than employing ℓ1or ℓ2loss function, we employ the objective function [25] (i.e., ℓ1with total variation (TV) regularization)under the assumption that TV penalty could constrain the smoothness ofIS R. DenotingIGTas the reference image, we have

where λ is the balanced weight. It is empirically found λ=1×10−5works well. We analyze the effect of different losses (e.g., charbonnier loss [6], perceptual loss [50]) in Section II.

IV. EXPERIMENTS

This section provides detailed experimental results to evaluate the effectiveness of the proposed model from different aspects. The implementation details are first presented, and then we offer a brief introduction to the used datasets. After that, experiments are carried out to verify the core component’s efficiency and the effect of different loss functions. Subsequently, quantitative and qualitative comparisons with several state-of-the-art approaches are conducted. Finally, experiments on real low-resolution images are also given.

A. Implementation Details

In each training mini-batch, we randomly cropped 16 color patches with a size of 48×48 from the LR images as input. We augment the training set with randomly rotating 90°and horizontal flips. Except the number of the input and output channels is 3 as the proposed model processes red-green-blue(RGB) image, the number of other internal channels is 48.

B. Datasets

We train WMRN model based on DIV2K dataset [52],which includes 800 2K-resolution images for the training set,another 200 pictures for validation and test sets. The LR images are downscaled from the reference HR image using bicubic downsampling. During the testing phase, we use five standard benchmark datasets for evaluation: Set5 [53], Set14[54], B100 [55], Urban100 [13] and Manga109 [56]. All PSNR and SSIM [57] results are calculated on the Y channelof the transformed YCbCr color space.

TABLE II INVESTIGATION OF WMRB MODULE. WE EXAMINE THE PSNR (DB) ON SET14 (×2) AND EVALUATE THE AVERAGE RUNTIME ON 100 DIV2K VALIDATION IMAGES (×2) WITH SAME TRAINING SETTINGS

TABLE III QUANTITATIVE EVALUATION OF DIFFERENT OBJECTIVE FUNCTIONS. WE COMPARE SEVERAL LOSSES ON THE B100, URBAN100 AND MANGA109 DATASETS (×4). OVERALL, THE LOSS FUNCTION ℓ totalHELPS TO IMPROVE VISUAL EFFECT

C. Analysis

Weighted multi-scale residual block:To show the effectiveness of the WMRB module, we validate the contributions of different components (mainly considering DS Conv, residual learning (RL), and weight scaling (WS)) in the proposed building block. The baseline is obtained without DS Conv(replaced by regular Conv layer), RL and WS. This model could gain better PSNR results but has a large number of parameters. To demonstrate the efficiency of DS Conv, we train our model with DS Conv-based WMRB module(denoted asMDS) and compare the performance with baseline.The quantitative results in Table II show thatMDScould highly reduce the parameters and Multi-Adds, and achieve a considerable performance. We then investigate the effect of residual learning (written asMRL) by adding three identity connections on the backbone part,subnet1, andsubnet2based on theMDS, respectively. As illustrated in Table II,MRLoutperforms theMDS; it increases by 0.04 dB. Furthermore,by combining weight scaling withMRL, our model shows a significant performance improvement (e.g., 0.41 dB on Set14 and beyond the baseline), which confirms the effectiveness of our weighted multi-scale residual block design.

D. Comparisons With State-of-the-Arts

We compare the proposed method with 11 advanced CNNbased SR methods, including SRCNN [19], FSRCNN [33],VDSR [20], DRCN [21], LapSRN [31], DRRN [22], MemNet[32], SRMDNF [58], IDN [37], CARN [26], AWSRN [9]. We note that the numbers of parameters and Multi-Adds are used to measure the model complexity, and we assume the output SR image with spatial resolution 1 280×720 to calculate Multi-Adds. The geometric self-ensembling strategy [8], [11] is used for further evaluation and marked with “+”. Since the source code of IDN is Tensorflow implementation at https://github.com/Zheng222/IDN-tensorflow, we rebuild it with Pytorch framework and the model size is really close to the original version (e.g., 579K vs. 590K (×2), 587.9K vs. 590K (×3),600K vs. 590K (×4)).

We show the reconstruction performance versus the Multi-Adds of CNN-based SR algorithms on the B100 dataset in Fig. 2, from which we can see that the proposed WMRN model is efficient in terms of the computational cost and achieves a superior performance among these CNN-based methods. Specifically, The WMRN model has Multi-Adds about 50% less than the CARN [26] and 60% less than the IDN [37]. This effectiveness mainly comes from the introduced novel module (i.e., weighted multi-scale residual block (WMRB)) and the post-upsample structure that is widely used in recent works [8], [23], [26].

Quantitative results with the state-of-the-art algorithms are listed in Table I. Note that we mainly compare models with roughly 2M parameters, these models have an approximately similar footprint as ours. Our WMRN model employs fewer parameters and Multi-Adds, while it performs favorably against the existing models on different scaling factors and benchmarks. Taking ×2 SR on the B100 set for example,using only about half of the number of CARN operations,WMRN gains comparable reconstruction performance against the computationally-expensive model.

As shown in Fig. 4 , we present visual comparisons on Urban100 dataset for ×4 scale. The qualitative comparison results demonstrate the recovered images by our proposed method are more visually pleasing.

E. Experiments on Real-World Photos

Fig. 4. Visual comparison for ×4 SR on benchmark testsets. Our method could reduce the spatial aliasing artifacts and generate more faithful and clear details.

Figs. 5 and 6 show an application of super-resolving realworld LR images with compression artifacts [35], [58] (e.g.,image Chip and Historical-007). The high-quality reference images and the degradation model are not available in these cases. The SelfEx [13] is used as one of the representative machine learning-based methods, and an advanced CNNbased algorithm AWSRN [9] is also included for comparison.

It can be observed from the examples that WMRN can reconstruct sharper and more accurate images than the competing methods. Specifically, as shown in Fig. 6 , the SelfEx and AWSRN series are affected by JPEG compression artifacts and tend to produce blurred edges while our method reconstructs more clear rails. Although WMRN could obtain better SR performance than the state-of-the-art approaches, it fails to recover very sharp details, as shown in Fig. 5. This phenomenon may be caused by training with a simple degradation model, like bicubic downsampling. For achieving better real SR performance, we need to develop a more general observation model and collect real-world datasets in the future.

V. CONCLUSIONS

In this work, we propose an effective weighted multi-scale residual network (WMRN) for real-time and accurate image super-resolution. The proposed weighted multi-scale residual block (WMRB) module adaptively utilizes the feature representations at different scale spaces via dilated convolutions with different rates. Besides, a global residual connection is adopted to ease the flow of information and add high-frequency details. Comprehensive experiments show the effectiveness of the proposed model.