A Novel Rolling Bearing Vibration Impulsive Signals Detection Approach Based on Dictionary Learning
2021-06-18ChuanSunHongpengYinYanxiaLiandYiChai
Chuan Sun,, Hongpeng Yin, Yanxia Li, and Yi Chai
Abstract—The localized faults of rolling bearings can be diagnosed by its vibration impulsive signals. However, it is always a challenge to extract the impulsive feature under background noise and non-stationary conditions. This paper investigates impulsive signals detection of a single-point defect rolling bearing and presents a novel data-driven detection approach based on dictionary learning. To overcome the effects harmonic and noise components, we propose an autoregressive-minimum entropy deconvolution model to separate harmonic and deconvolve the effect of the transmission path. To address the shortcomings of conventional sparse representation under the changeable operation environment, we propose an approach that combines K-clustering with singular value decomposition (K-SVD) and split-Bregman to extract impulsive components precisely. Via experiments on synthetic signals and real run-to-failure signals,the excellent performance for different impulsive signals detection verifies the effectiveness and robustness of the proposed approach. Meanwhile, a comparison with the state-of-the-art methods is illustrated, which shows that the proposed approach can provide more accurate detected impulsive signals.
I. INTRODUCTION
ROLLING bearings are important in almost every motors and rotary based machinery, such as wind turbines,automotive transmission systems, aero-engine, etc. These devices usually operate in harsh working conditions influenced by high speeds, heavy loads, high-low temperature,and contamination. It is therefore highly desirable to monitor the condition rolling bearings to improve their availability,safety, and reliability, thereby reducing system operation and maintenance costs, minimizing downtime, and maximizing productivity [1], [2]. Rolling bearings are the primary components in these devices, from which most failures may start. It is necessary to diagnose the faults as early as possible to prevent grave or catastrophic accidents.
Vibration signal analysis is a key topic in rolling bearing fault diagnosis research because of its ease of measurement.When localized faults (e.g., cracks, a small hole, a pit, or a missing piece of material on the surfaces) of rolling bearings occur, the vibration impulsive signal would be created a ball passes through the defect [3]. The impulsive signal contains many fault information which must be extracted. However,the vibration impulsive signal is usually coupled with impulsive components, background noise, harmonic components, amplitude modulation, and frequency modulation (AM-FM) signals [4]. Besides, the vibration impulsive signal collected from bearings is normally non-stationary and nonlinear, and the impulsive components are usually too weak to be distinguished. Therefore, it is still a challenge to detect the impulsive signals for fault diagnosis under high noise levels and strong harmonic interference.
To reduce background noise and heavy harmonics to extract the impulsive signal from the vibration, sparse representation(SR) has attracted much attention in bearing fault diagnosis[3]. As fault signals of the rolling bearing are structural, SR can efficiently detect impulsive signals from rolling bearing vibration signal, which mines the low-dimensional intrinsic subspace of faulty information from the complex vibration signal via solving an optimization problem [5]. It can effectively solve the problem of frequency aliasing and is more in line with the physical explanation. Nowadays, more and more research focuses on SR-based impulsive signal detection. For example, Heet al. [6] proposed a novel approach based on sparsity overlapping group sparsity to extract repetitive transients in the time domain. Dinget al. [7]developed an augmented Lagrangian majorizationminimization algorithm for impulsive feature detection of faulty bearings and gear boxes. A resonance-based signal decomposition method was also proposed for extracting nonoscillatory transients [8]. However, they only consider the influence of the noise and ignore the influence of strong harmonics (or AM-FM signals). Caiet al. [9] introduced a sparsity-enabled feature extraction method, the representative dictionary was set as a tunable Q-factor wavelet transform and the sparse prior was fixed asL1-norm. With a new family of model-based impulsive wavelets, Qin [4] proposed a SRbased method to detect the weak transient feature of rolling bearings. Yanget al. [10] proposed a SR method based Fourier dictionary to separate the harmonic components.These methods are effective in fault diagnosis and signal processing, but require a large amount of prior knowledge.The choice of a fixed dictionary directly affects the representation effectiveness, which is difficult to implement in impulsive signals reconstruction under the changeable operation environment, complex components, and nonstationary conditions.
Dictionary learning is an effective data-driven method to construct an empirically learned dictionary for sparse representation. Since the atoms in dictionary come from the underlying empirical data rather than from some theoretical models, this makes it possible to obtain a better sparse representation [11]. Dictionary learning can capture higher level features of signals, thus building an overcomplete dictionary and sparser representation, which has been proved to be effective in image denoising and text detection [12],[13]. Many representative dictionary learning-based methods has been reported, such as K-clustering with singular value decomposition (K-SVD) [14] and clustering-based sparse representation [15]. In recent years, dictionary learning methods have emerged in 1-D time-series signal processing for bearing fault diagnosis [16], [17] and vibration impulsive signals denoising [18], [19]. Although most of the dictionary learning based methods have achieved competitive performance for vibration impulsive signal processing compared to the state-of-the-art, there are three main open problems in impulsive signals detection based on dictionary learning: 1) How to construct a more efficient decomposition algorithm for harmonic components; 2) How to reduce noise without destroying the inner structure of impulsive signal to build an appropriate dictionary; 3) How to precisely extract the impulsive component over learned dictionaries in the case whereL1-norm always underestimate the amplitude of impulses easily.
Motivated by these, we propose a novel impulsive signals detection approach based on dictionary learning for a singlepoint defect rolling bearing vibration signal detection. In this work, we analyze in detail the dynamic process in the case of defect fault, and theoretically develops the physical link between bearing faults and vibration signal’s components. For harmonic components, which are generally sinusoidal or cosinusoidal, so an efficient autoregressive (AR) algorithm based linear prediction is proposed to precisely and rapidly separate the harmonic components. This model not only reduces the computational complexity, but also improves the speed and accuracy of harmonics separation. To build an appropriate dictionary in K-SVD, an improved minimum entropy deconvolution (MED) searches for an optimum set of filter coefficients that effectively clarifies the impulsive signals and increases the signal-to-noise ratio (SNR).Furthermore, it can deconvolve the effect of the transmission path. To guarantee that specific conditions of the penalty parameters are derived, an adaptive parameter estimation split-Bregman (SB) algorithm [20] is proposed to decouple theL1- norm andL2-norm terms and solve them alternatively until convergence.
The main contributions can be summarized as follows:
1) An AR algorithm based linear prediction is used to estimate frequencies and phases of harmonics, which can efficiently separate harmonic components.
2) An improved MED model is used to weaken Gaussian noise without destroying the inner structure of impulsive signals, which improves the quality of the training dataset to build an appropriate dictionary.
3) A novel adaptive parameter estimation SB algorithm is proposed to solve the problem thatL1-norm underestimates the amplitude of impulses, which accurately extracts the impulsive signal.
The remainder of this paper is organized as follows. Section II analyzes the dynamic process in the case of defect fault and the difficult problems of impulsive signals detection. Section III describes the basic mathematical details of impulsive signals detection approach based on dictionary learning. In Section IV,two experiments prove the effectiveness of the proposed method, the performance of the proposed method is also compared with those of other literature methods. Finally, the conclusion of this work and possible future extensions are discussed in Section V.
II. ROLLING BEARING STRUCTURE AND SIGNAL
Rolling bearings generally consist of an inner ring, an outer ring, a rolling element, and a cage, as shown in Fig. 1. Rolling elements are bound by a cage which enables uniform distribution of the rolling elements and guides the rolling elements to rotate for lubrication. Rolling bearing faults can be classified as distributed and localized defects [21].Distributed defects are distributed throughout the region,which, compared with localized defects, is difficult to characterize by specific fault-related frequencies. Therefore,distributed defects are rarely considered in modern diagnosis techniques, and vibration impulsive signals detection only focus on localized defects, because the characteristic fault frequency is a clear indicator of damage [22].

Fig. 1. Rolling bearing structure and load distribution.
A single-point defect could be considered as a small hole, a pit, or a missing piece of material on the corresponding element. Vibration impulsive signals are created as a ball passes through the defect. Due to other factors, the vibration impulsive signals contain the harmonics components, periodic impulsive components, and noise. The observed vibration signals(t) of a faulty rolling bearing often can be modeled as

wheresP(t) denotes a pseudo-cyclostationary (approximately periodic) impulsive component,sH(t) denotes the harmonic(or AM-FM signal) component, andn(t) denotes noise.
A. Periodic Impulsive Component
In a rolling bearing with single-point defect, vibration impulsive signals arise when a ball passes through the defect illustrated in Fig. 2. According to [23], the periodic impulsive component is described as follows:

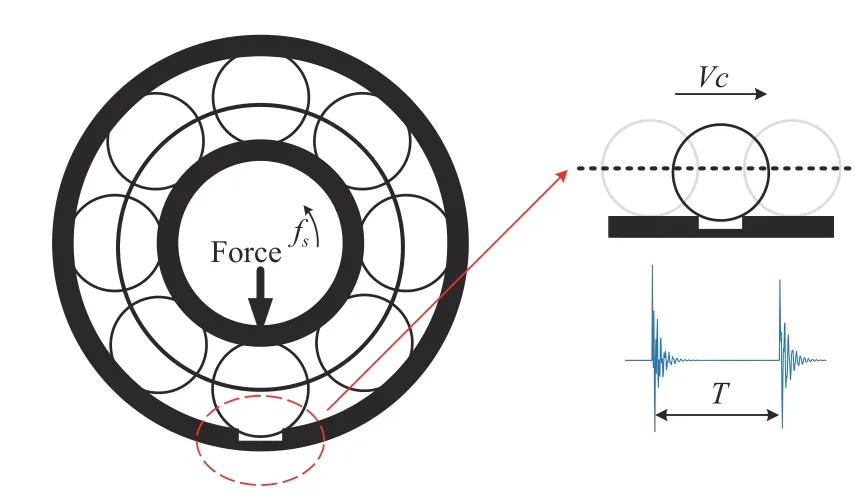
Fig. 2. Sketch of the passing process of the rolling element across the defect.
B. Harmonic Component
Since the limited manufacturing precision and the nonstationary operating environment, the physical structure of the rotor in rotating machinery systems is neither completely symmetrical nor axisymmetric, and it is not completely coaxial with the bearing. These factors lead to many unbalances and misalignments, which can cause modulation effects and generate harmonic signals in vibration impulsive signals when the motor starts running. This is a fundamental transient phenomenon that is always modeled as a dynamic response of abnormal operations when the generator develops local malfunction [24]. The harmonic component can be represented as
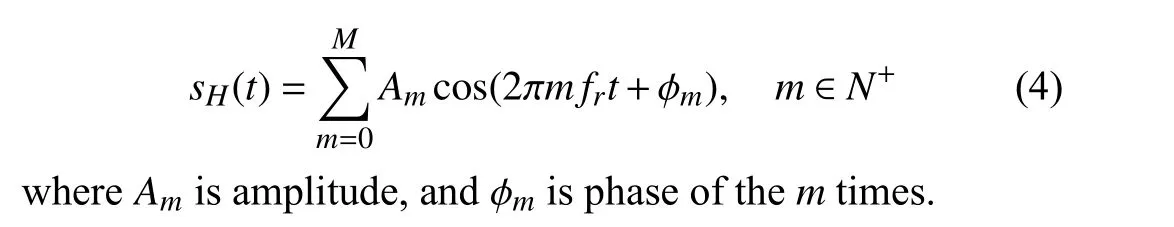
C. Noise
In many rotating machinery systems, there are heavy noises,stemming from sensor imperfections, poor running environment, or communication errors, etc. [10], which can easily distort vibration impulsive signals. Specifically, it can be caused by its structural factors, such as radial clearance,rotating speed, load, and vibration of rotating shaft [25].According to the source, they are classified as rotating noises,resonant noises, ventilating noises, bearing noises, or other background noises. According to the signal structure, they can be classified into either Gaussian noises or small impact noises.
III. PROPOSED ALGORITHM
Impulsive signal detection is used to extractsP(t) froms(t)with the fault information. However,s(t) has three signals coupled to each other, which makes it difficult to accurately extractsP(t). Especially for early fault signal detection,sP(t)is so weak that is easily submerged in noise and other components. Moreover, due to transfer along a path,modulation phenomenon may arise. To solve these difficulties, a novel rolling bearing impulsive signals detection approach based on dictionary learning is proposed, which mainly includes three steps: harmonic components separation,background noise separation, and impulsive components extraction. The detailed implementations for the proposed impulsive signals detection approach based on dictionary learning are shown in Fig. 3.
A. Harmonic Component Separation
Since many unbalances and misalignments exist in many rotating machinery systems, which can cause modulation effects and generate harmonic signals in vibration impulsive signals. Consequently, this influences the result of impulsive feature detection. The vibration signal in (1) is mixed with the harmonic componentsH(t) which usually consists of sinusoidal waves. The AR model algorithm [26] is to remove the harmonic signals from the original vibration signal. For vibration signals(t), thep- th order AR(p) model [27] is defined as follows:
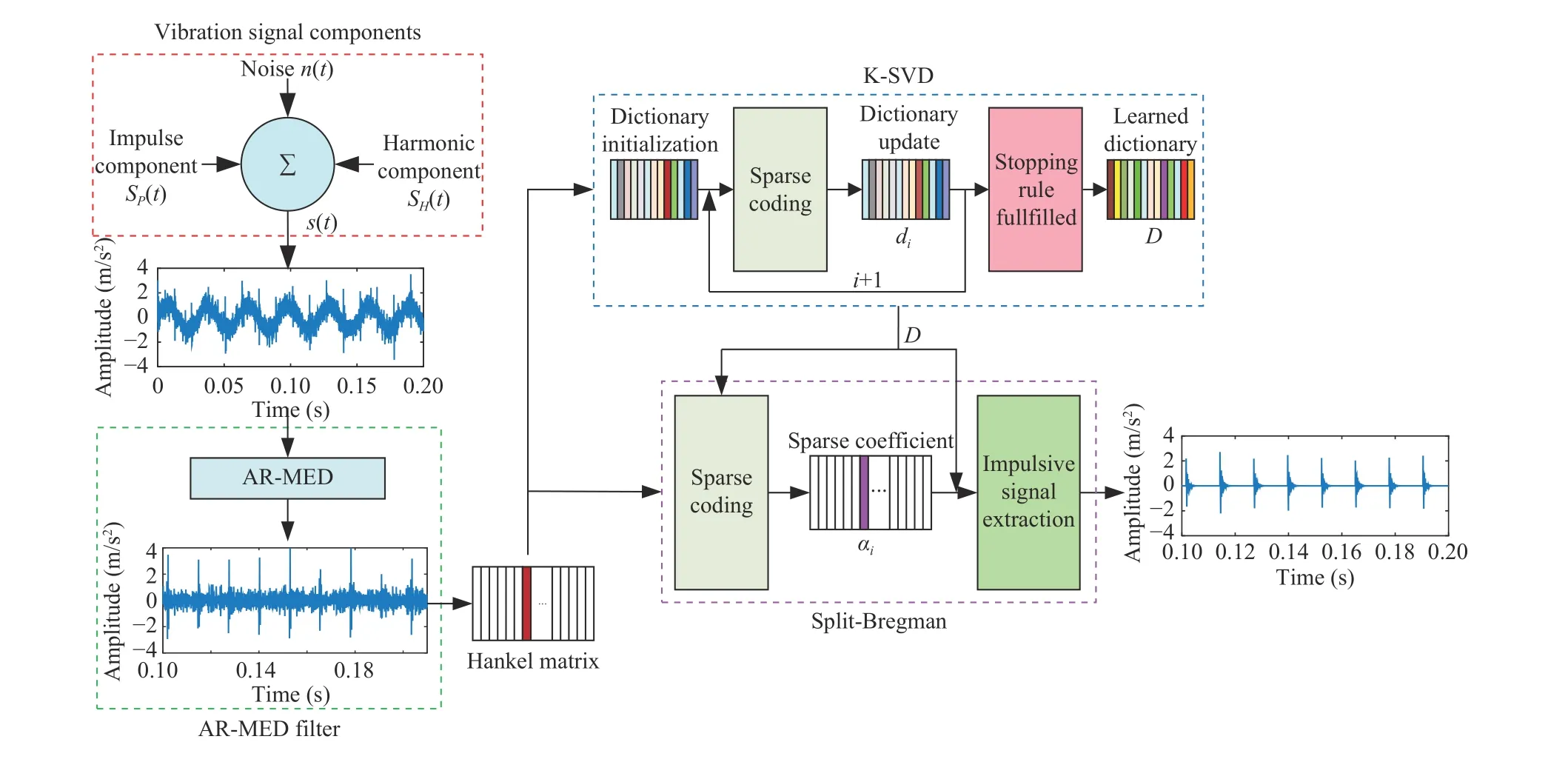
Fig. 3. The detailed implementations for the proposed impulsive signals detection approach based on K-SVD and AR-MED.

Usually, in order to ensure that ϵncontains impulsive signals[28], the order of AR model should be less than the spacing between two consecutive impulses. The Akaike information criterion based on maximum likelihood principle [29] is presented to determine optimal order. AR coefficients φiare estimated through Yule-Walker [30].
As a consequence, by subtracting the harmonic parts from the original vibration signal, the residual signal can be obtained including the impulsive components and background noise.
B. Background Noise Separation
After AR model processing, the vibration signals contain the remaining impulsive componentssP(t) and background noisen(t). Due to the diversity of faults and the non-stationary operating environment in rolling bearing systems, it is hard to choose a proper pre-defined dictionary to fit the impulsive signals. Therefore, the dictionary learning algorithm is expected to be developed for learning latent structure of impulsive signals. Through the analysis of noise in Section II,however, heavy noise may destroy the original signal structure, which will lead to the learning of noise atoms during the dictionary learning process. In addition, dictionary learning may perform poorly for denoising the early fault signal which is under heavy noise. Thus, it is necessary to find a way to overcome this difficulty.
1)Minimum Entropy Deconvolution for Signal Denoising:Recently, MED in [31] has been developed for rolling bearing fault diagnosis, which is based on information entropy that is a characteristic index of fault diagnosis. For process of MED[32], it is very important to design a suitable finite impulse response (FIR) filter, from which the output will enhance the impulsive components. Let the measured signals˜(n) in discrete form be:

To recover the impulsive signals, an optimal inverse filterg(n)should be developed in MED.
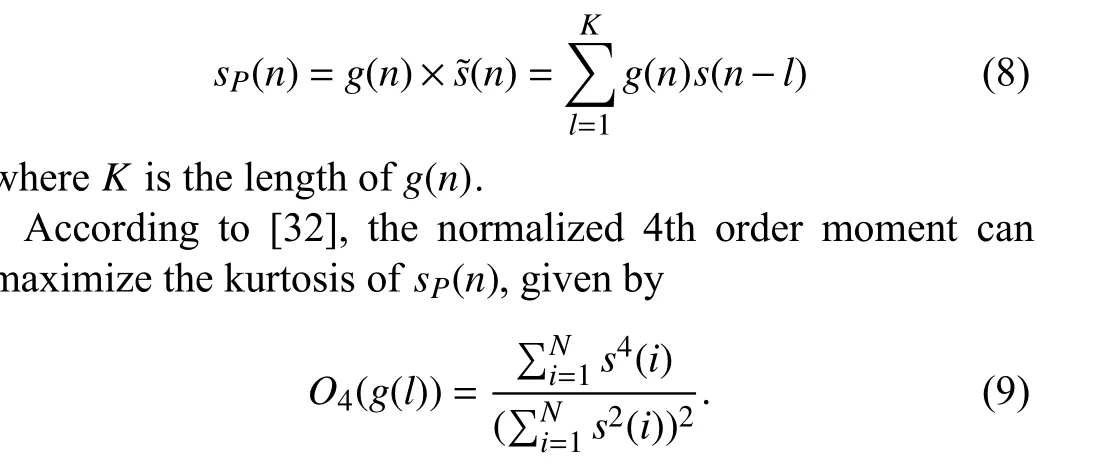
By taking the partial derivative with respect tolfor (8), we have:
2)K-SVD for Dictionary Learning: After MED denoising,vibration impulsive signals remain the combination of impulsive signals and weak noise.sˆ(t)=sP(t)+nˆ(t), where ˆn(t) is white noise and other small impulsive signal.Dictionary learning can be expressed as an optimization problem, where we look to calculate an overcomplete dictionary with minimizing error under the sparsity constraint.

The process of dictionary learning consists of the sparse coding and the dictionary updating. The difference between these algorithms is mainly in the dictionary update mode,because the coefficient update part has no essential difference in most algorithms. Updating sparse coefficient based on fixed dictionary is a standard sparse coding problem. Method of optimal directions (MOD) [33] and K-SVD [14] are the most popular dictionary learning algorithms, whereas K-SVD is more efficient in the dictionary update stage.

C. Impulsive Component Extraction
After the background noise separation and dictionary learning stage,sP(t) can be represented by a linear combination of some atoms by learnedDwhich is similar to impulsive signal. The rolling bearing vibration impulsive signalssP(t) admits a SR with respect to an invertible linear transformationsP(t)=Dα. Therefore, SR is equivalent to the optimization problem:

where α is the representation and λ is the regularization parameter, which maintains balance between the signals fidelity and sparsity. The approximate problem can be further formulated as “elastic-net” [34]:


The skrinkage method is effective and stable, and requires only a few operations. In experiment, a few iterations were required for the splitting stage. The extracted impulsive signals can be reconstructed via:

IV. EXPERIMENTS AND DISCUSSIONS
In the design and study of rolling bearing vibration impulsive signals detection schemes, it is very important to verify if the designed signal detection approach can detect impulsive signals. Two experiments are performed, the first of which is performed on the synthetic signals based on the mechanical vibration model, and the other experiment signals based on the test bench of the Case Western Reserve University (CWRU) Bearing Data Center [37]. Both experiments are verified by many comparative methods.
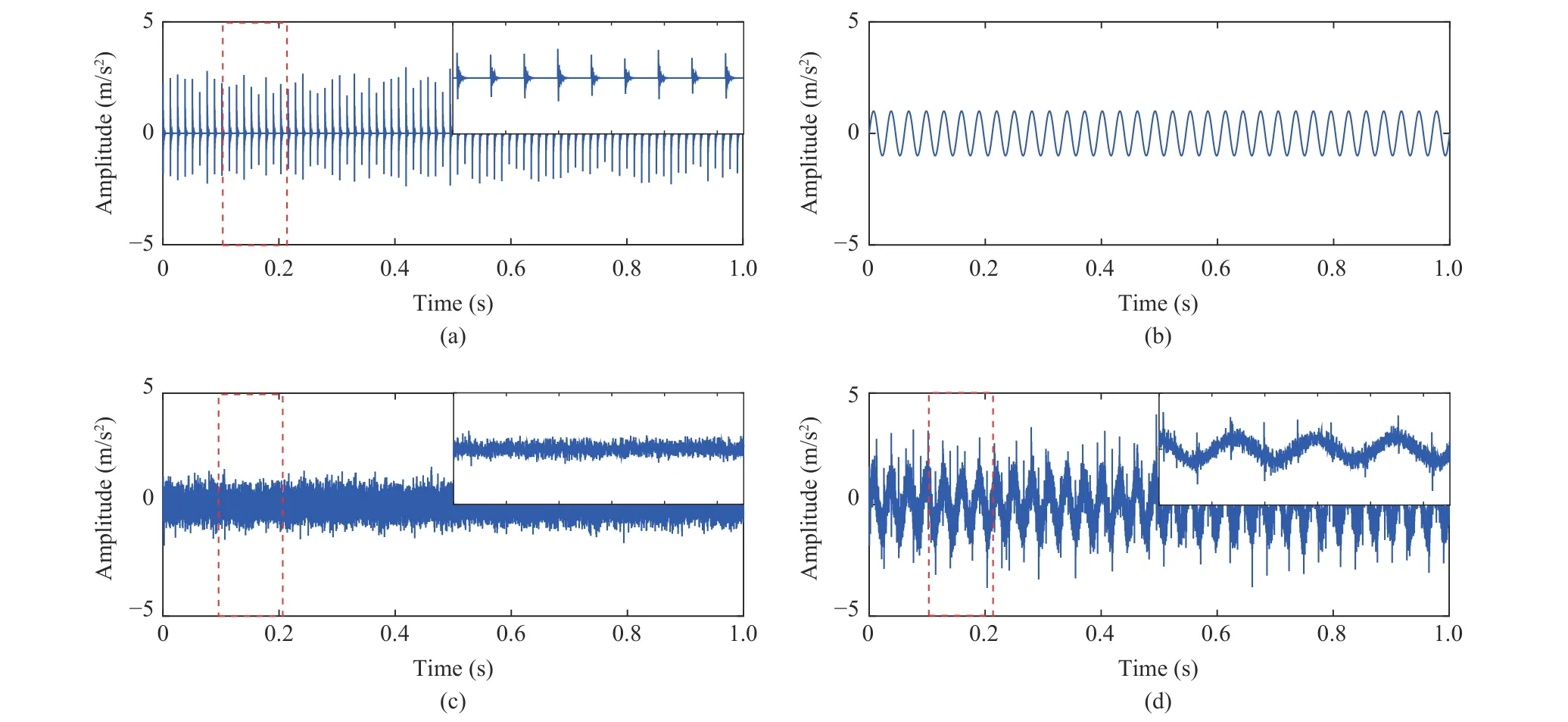
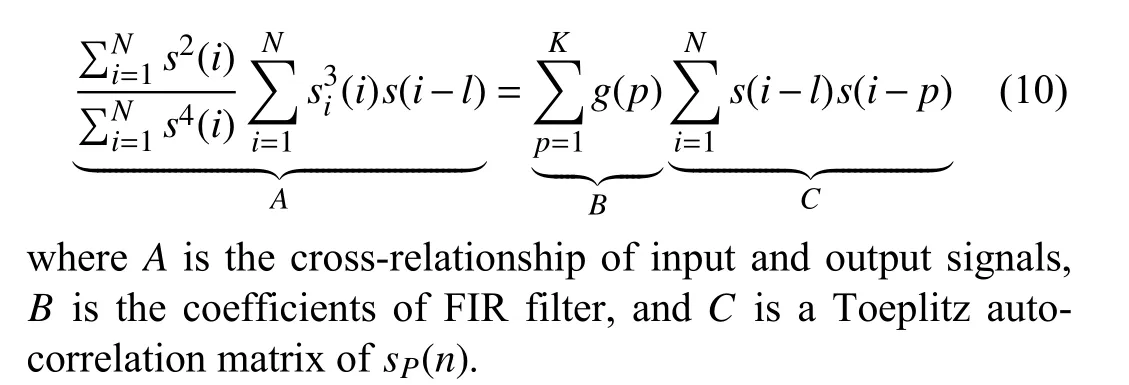
Fig. 4. Simulation siganls. (a) Impulsive siganls; (b) Harmonic siganls; (c) Noise; (d) Synthetic siganls.

Fig. 5. The detected impact signal processed by K-SVD. (a) AR-MED filtered signal; (b) Detected impulsive signal; (c) Envelope spectrum; (d) The effect of SNR on RA.
A. Experiment on Synthetic Signals
To evaluate the performance of the proposed approach, the synthetic signals are constructed for vibration impulsive signal detection. According to (2)-(3) in Section II, the type NUP311EN rolling bearing is used to determine structural parameters, specificallyDb=18 mm,Dc=85 mm,NB=13,fh=33 Hz and α=0°. The ratational speed is 600 rpm, i.e.,the rotational fraquencyfr=10 Hz . So,fo,fi,fbandfcare 51.24 Hz, 78.76 Hz, 22.55 Hz and 3.94 Hz, respectively. Two order natural frequencies are defined asfd1=2500 Hz,ζ1=0.08,fd2=8000 Hz , ζ2=0.05, respectively.
According to the Nyquist-Shannon sample theorem, the sampling frequency should be at least twice as much asfd. In this simulation, set sampling frequencyfsas 20 000 Hz and sample time periodTsas 1s. The white noise (- 5 dB) is added to the pure impact signal, the waveforms of a synthetic signal are shown in Fig. 4.
From Fig. 3, the simulated signals are processed and the results are shown in Fig. 5. The harmonic signals are separated from the simulated signal by AR-MED Filter displayed in Fig. 5(a). By comparing the results before and after filtering, an obvious conclusion that the harmonic separation has been completely filtered out. Besides, the MED has an obvious denoising effect comparing with Fig. 4(c).
After the AR-MED filter, the simulated signal is only left with impact components and weak noise. The processed signals are turned into the Hankel matrix for dictionary learning, with the parameters of the improved K-SVD selected as Table I. The hyperparameters μ and λ of SB are small positive fixed values set as 0.05 and 0.07, respectively. The training set is constructed as the Hankel matrix, which is based on intercepting the 0.1s to 0.21s simulation signal. The size of the learned atom shown in Fig. 6 should be bigger than the duration time of oscillation and smaller than the time interval between two impacts. The detected impulsive components based on the proposed approach are shown in Fig. 5.(b). Comparing Fig. 5(b) and Fig. 4(d), it can be seen that the harmonic component has been completely separated,and the periodic impact components are clear under the heavy noise environment. The Hilbert transform-based envelope spectrum of the detected signal is shown in Fig. 5(c), from which the inner fault characteristic frequencyfi(78.76 Hz) can be markedly identified. Our design is run on Windows 10 Professional, containing Intel Core i5-7500 CPU 3.4 GHz,8 GB RAM, and 500 G HARD DISK. The execution time of program consumes 12.2 s. To further verify the convergence of the algorithm, we design aERR=mean(|αi|0)=|α|/N,where α is the representation andNis atom number. The result is shown in Fig. 7.

TABLE I THE PARAMETERS OF K-SVD

Fig. 6. Atom learnt by the proposed approach.

Fig. 7. The convergence of algorithm.
To explain the problem of inefficient detection of impulsive signals in a heavy noise environment by the K-SVD method,introducing reconstruction accuracy to explore the effect of SNR on detection ability. The reconstruction accuracy (RA) is defined as ‖sˆP(t)‖2/‖sP(t)‖2×100%. The parameters of KSVD are the same as Table I. Fig. 5(d) shows the effect of SNR on RA. Note that for SNR = 0 dB is the turning point,and when it is below 0, RA decreases sharply. When SNR =-5.2 dB, the RA is less than 80%. The changing trend of RA shows that K-SVD is very sensitive to noise. The heavy noise will destroy the original signal structure, which leads to the learning of noise atoms in the dictionary learning process.
As a comparison, we use MED and K-SVD for comparison our experiments. Since two methods cannot separate harmonic components, the signal in which harmonic components have been removed is tested. Comparing the results of Figs. 8(a)and 8(b), it shows that K-SVD is a better method than MED.Comparing Fig. 8 and Fig. 5(b), the comparison clearly illustrates that the denoising ability is limited when two methods are used respectively.
To further illustrate the accuracy and effectiveness of the proposed approach, compared it with other methods found in the literature, including wavelet transform [38], sparse representation [39], segmented K-SVD, and sliding window denoising K-SVD (SWD-KSVD) [23]. Similarly, the four methods do not have harmonic separation power. As before,the synthetic signals are the missing harmonic component. To make the comparison more convincing, the length of the atoms is set to that of the previous experiment. The comparing results obtained by four methods are shown as follows Fig. 9.
It can be seen that the signal detection effects of the other four methods are not as good as the proposed approach.Further analysis of Fig. 9, the wavelet transform performed the worst, the detected signal residuals a lot of noise, and the impulsive components are not obvious. In comparison, the methods of dictionary learning are better than traditional methods. However, there are small amounts of impact noise in the reconstructed signal, shown as Figs. 9(c) and 9(d). RA can quantify the detected signals and compare them numerically with other methods. Comparison of the detection results of the four methods in different fault signals are shown in Table II.
In the simulation tests, the AR-MED filter separates harmonic components and clarifies impulse, the improved KSVD can build a suitable dictionary in which the learned atom is close to the simulation impact signal. The detected impulsive signals are clear and the RA are more accurate compared with traditional methods. Meanwhile, the proposed method shows excellent performance under heavy noise.
B. Outer Ring Fault Experiment Signal
In the actual test, the vibration impulsive signals were collected by an experimental setup from the Case Western Reserve University Bearing Data Center [37], which have been used by many scholars in machinery diagnosis. Single point faults were set on the testing drive-end bearings separately at bearing components using electric discharge machining methods. The resulting vibration from the motor was measured by accelerometers being mounted to the motor’s shell with magnetic bases, at a sampling frequency of 1 2 kHz.Table III lists the parameters of bearing information.
In this experiment, a vibration signal with a motor load of 0 and a fault diameter of 0.007 inches is selected. The approximate speed is 1797 rpm. Based on the fault characteristic frequency of the outer race and the rotation frequency, the corresponding characteristic frequency was calculated to be ( 1797/60)×3.585 ≈ 107.37 Hz for this case as listed in Table III. One segment of the vibration signal is displayed in Fig. 10.
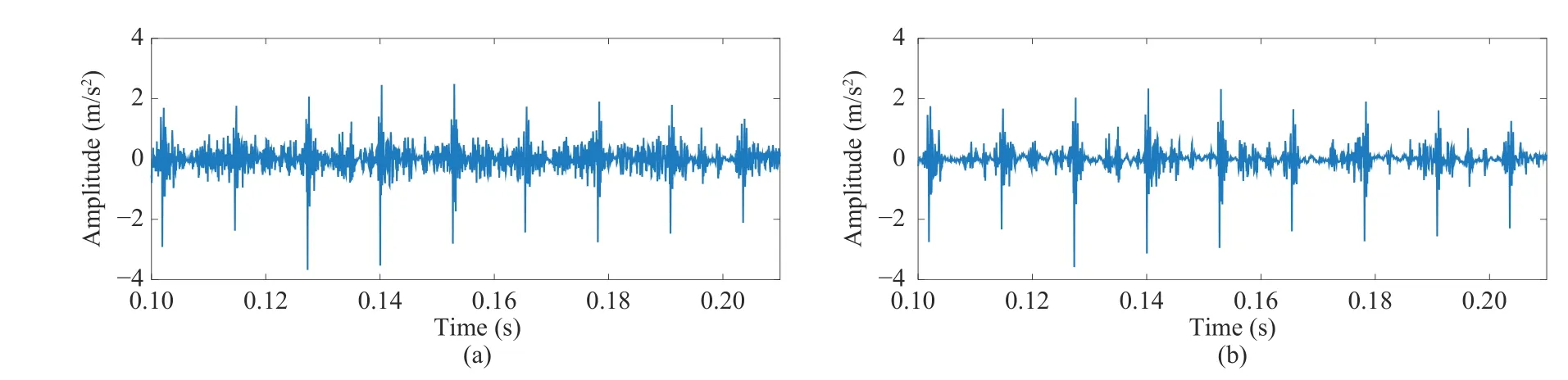
Fig. 8. The detected impulsive signal using MED and K-SVD respectively. (a) Using MED only; (b) Using K-SVD only.
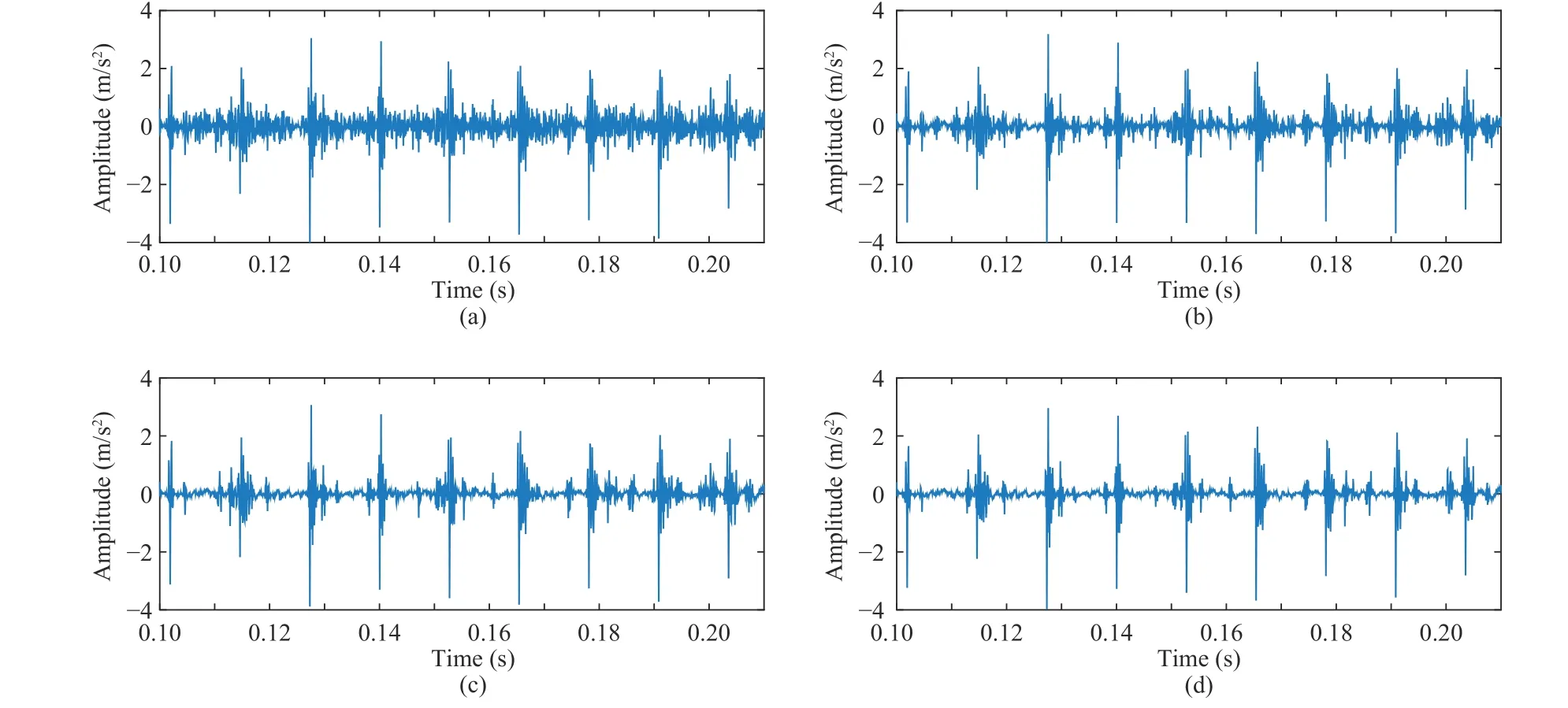
Fig. 9. The detected impulsive signal by other methods. (a) Wavelet transform; (b) Sparse representation; (c) Segment K-SVD; (d) SWD-KSVD.

TABLE II THE RA OF DIFFERENT FAULT SIGNALS BASED ON FIVE METHODS

TABLE III TYPE: 6205-2RS JEM SKF, BEARING INFORMATION [37]
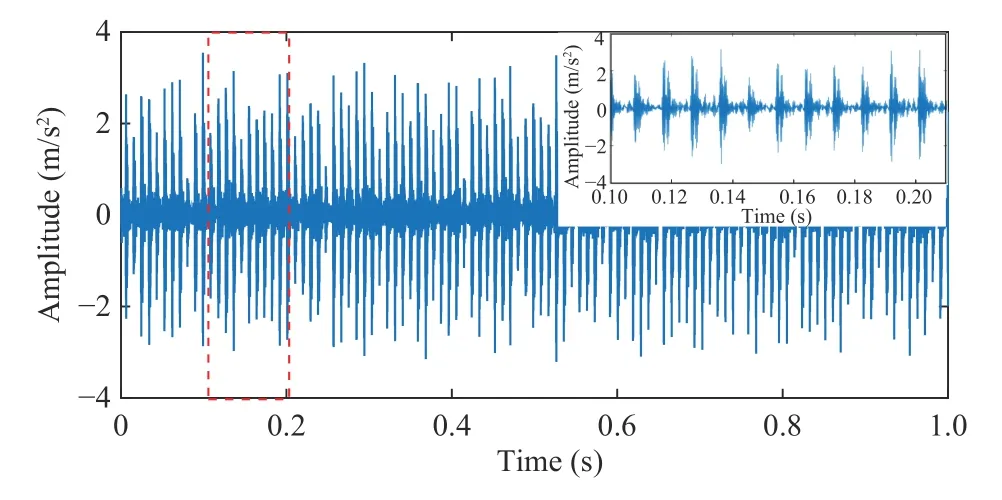
Fig. 10. Analyzed signal.
The vibration signal from 0.1 s to 0.21 s is detected by the proposed approach. After five iterations, the learned atom is illustrated in Fig. 11 and is very close to the structure of impulse. In Fig. 12, the impulsive signals appear periodically without any noise. Meanwhile, the outer ring fault frequency is calculated as 107.37 Hz and the impulse interval is 9.314 ms.It is in complete agreement with the experimental results of Fig. 12. In contrast to the segment of Fig. 10, it is apparent that the noise component has been removed and the pulse component is completely preserved.
For comparison, the same vibration impulsive signals are used by MED and K-SVD algorithms respectively. According to the results shown in Fig. 13, it is obvious that detected impulsive signals are not as clear as the result of the proposed approach in Fig. 12, as some noise has remained. It also can be seen from the figure that the results obtained using K-SVD are more clear compared with the results of MED algorithm.In Fig. 13(a), the MED is used to enhance impulsive signals by information entropy. Comparing Fig. 13(a) and Fig. 12,there is a lot of white noise between impulses in the result of the detected impulsive signal by MED, which is not as accurate as the proposed approach. In Fig. 13(b), since KSVD is sensitive to heavy noise, the results are not as good as the proposed approach, but better than the results from MED.Therefore, these two methods are inefficient for vibration impulsive signal denoising.
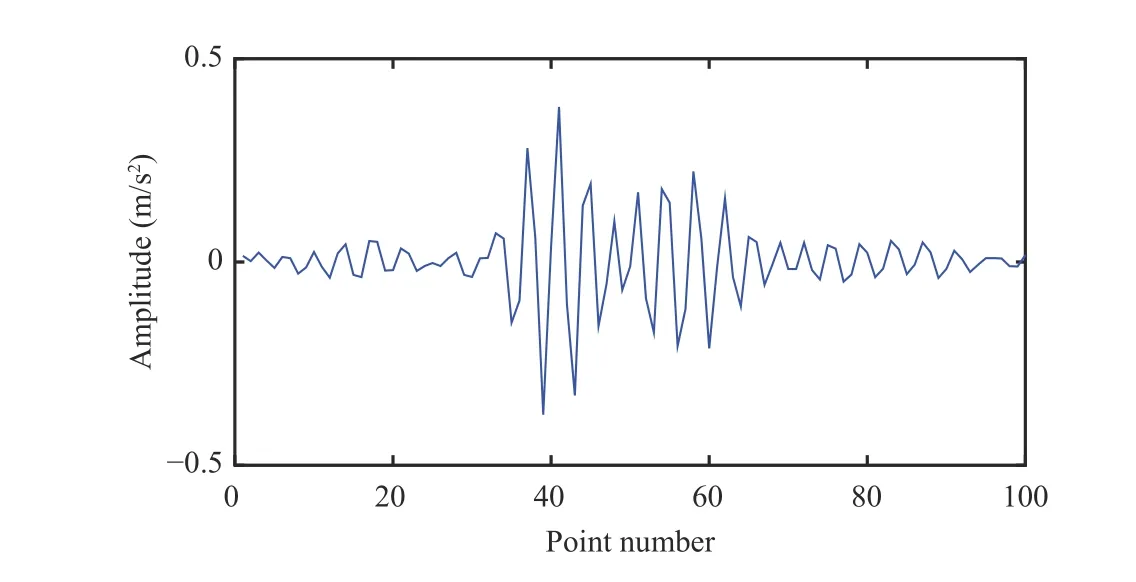
Fig. 11. Waveforms of the learned atom.

Fig. 12. Results obtained by the proposed method.
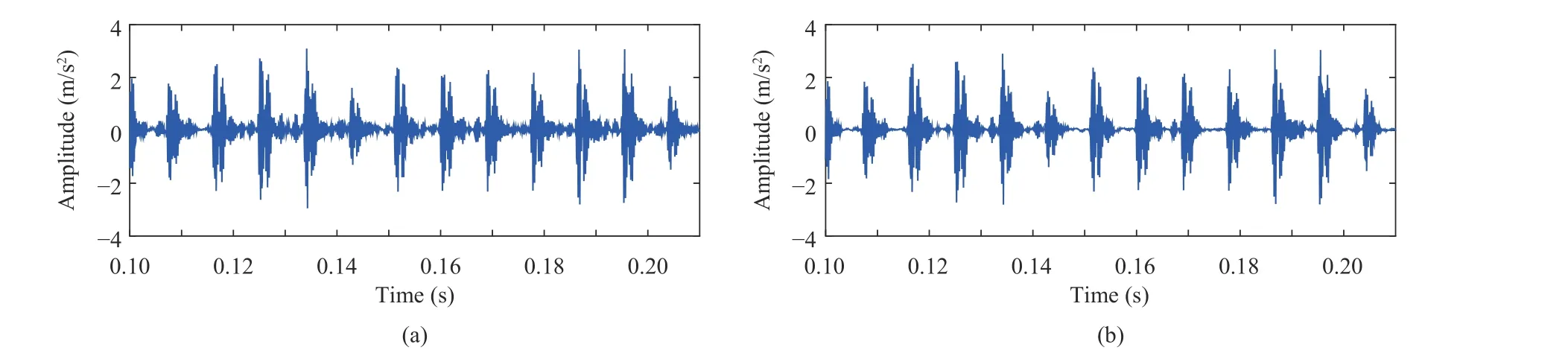
Fig. 13. The vibration signal using MED and K-SVD respectively. (a) Using MED only; (b) Using K-SVD only.
To prove the universal applicability of the proposed method,it is applied to different working conditions, including different damage sizes, different loads, and different speeds.According to the characteristics of bearing operation under different conditions, the following experimental data are described in detail in Table IV for comparison. All reconstructed impact signals are displayed in Fig. 14.

TABLE IV DESCRIPTION OF EXPERIMENTAL DATA
The proposed method’s good performance in signal denoising can be seen through the four situations. No. 1 of Table IV is for a fault diameter of 0.007 inches, which can be regarded as an early fault vibration signal denoising. It can be seen from the results that there is a very obvious periodic pulse component, which not only preserves the time domain characteristics of the pulse signal, but also filters out the noise signal. No. 2 of Table IV is collected by the accelerometer at Fan end. The time waveform is shown in Fig. 14(a2), which is very unclear periodic impulsive components. In this case, it can be seen as weak signal detection under a heavy noise environment. The weak signal is not only a small amplitude,but mainly the signal that is easily submerged by noise, and exhibits a low SNR, thus making denoising a difficult problem. Although the original pulse component has been damaged by noise, the result in Fig. 14(b2) shows distinct periodic impulsive signal. Similarly, the proposed method can also be applied to signal denoising of different motor loads.
V. CONCLUSIONS AND DISCUSSIONS
In this paper, we presented a novel data-driven impulsive signal detection approach based on dictionary learning. This approach solves the problem of impulsive signal detection of weak faults in which three components are coupled to each other. An AR-MED model clarifies the impulsive components and weaken other components to improve the quality of the dictionary learned by K-SVD. A novel adaptive parameter estimation SB algorithm accurately extracts the repetitive impulsive components. This approach has many advantages compared with traditional sparse representation methods, as neither prior knowledge nor a predefined dictionary are required. The RA of detected impulsive signals reaches about 90%. Moreover, the combination of K-SVD and AR-MED methods can overcome the disadvantage of K-SVD where it is sensitive to heavy background noises when building a dictionary. Via experiments on both fault synthetic signals and actual run-to-failure signals, the verification results demonstrate that the proposed approach can effectively remove harmonic signals and background noise, and it is robust and works well under different working conditions.However, the current method is somewhat complicated for the signal separation stage and can only be used to resolve a single fault. We aim to dedicate more attention to investigating a more efficient, and compact separation algorithm, composite fault detection and the improvements of parameter self-adaption in the future work.

Fig. 14. Comparison of different conditions. (a) The time waveform of vibrational signal; (b) Result obtained by the proposed method. The number corresponds to the number in Table IV.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Speed and Accuracy Tradeoff for LiDAR Data Based Road Boundary Detection
- Distributed Asymptotic Consensus in Directed Networks of Nonaffine Systems With Nonvanishing Disturbance
- Finite-Time Fuzzy Sliding Mode Control for Nonlinear Descriptor Systems
- Dual-Objective Mixed Integer Linear Program and Memetic Algorithm for an Industrial Group Scheduling Problem
- Output-Feedback Based Simplified Optimized Backstepping Control for Strict-Feedback Systems with Input and State Constraints
- Empirical Research on the Application of a Structure-Based Software Reliability Model
