Distributed Asymptotic Consensus in Directed Networks of Nonaffine Systems With Nonvanishing Disturbance
2021-06-18QinglingWangandChangyinSun
Qingling Wang, and Changyin Sun,
Abstract—In this paper the distributed asymptotic consensus problem is addressed for a group of high-order nonaffine agents with uncertain dynamics, nonvanishing disturbances and unknown control directions under directed networks. A class of auxiliary variables are first introduced which forms second-order filters and induces all measurable signals of agents’ states. In view of this property, a distributed robust integral of the sign of the error (DRISE) design combined with the Nussbaum-type function is presented that guarantees not only the desired asymptotic consensus, but also the uniform boundedness of all closed-loop variables. Compared with the traditional sliding mode control(SMC) technique, the main feature of our approach is that the integral operation in the proposed control algorithm is designed to be adopted in a continuous manner and ensures less chattering behavior. Simulation results for a group of Duffing-Holmes chaotic systems are employed to verify our theoretical analysis.
I. INTRODUCTION
THE cooperative control of multi-agent systems (MASs)has received a large amount of attentions in the last several decades, where the design of distributed control algorithms for consensus of MASs has been the fundamental task due to its considerable applications [1]-[6]. Besides,consensus control for nonlinear MASs is technically important since the unknown nonlinear dynamics usually exist in practical applications, where many important works have been reported [7]-[13].
Recently, the researchers have mainly focused on the distributed consensus problem of nonaffine systems, and several control algorithms have been developed [14]-[17]. A distributed adaptive consensus tracking algorithm was proposed for the MASs in nonaffine pure-feedback form by using the backstepping technique, neural networks (NNs), and the dynamic surface control method in [14]. In [15], a class of distributed consensus tracking algorithms with the continuous control action were developed for networked nonaffine MASs to ensure that the tracking error can converge to a small region within a prescribed finite time. In [16], by using output constrained feedback, a distributed consensus algorithm was proposed for nonaffine MASs subject to partially unknown control directions to drive the agents’ states to the region of predefined constraints. An adaptive filtered backstepping control method is employed to achieve the cooperative tracking of uncertain nonaffine MASs with input nonlinearities and unknown control directions in [17]. It is worth noting that most existing results have widely utilized the technique of NNs to cope with the unknown system dynamics,since NNs have the ability of approximating smooth,unknown nonlinear dynamics. However, NNs based approaches mainly focus on the process of choosing units and neurons for the NNs, which increases the burden in adjusting parameters. Furthermore, it is known that NNs can not approximate nonlinear dynamics that depend on the time variable.
Another challenge for consensus algorithms is the distributed control design of MASs with nonvanishing disturbance, where it requires the use of an advanced robust control scheme. When addressing nonvanishing disturbances,the NNs based approaches are not capable of providing satisfactory performance, such as the asymptotic convergence of system states. Therefore, disturbance observers should be designed to reject the unknown disturbance [18], [19]. As an alternative approach, the sliding mode control (SMC) method is well known for its disturbance rejection property [20].Sliding mode observers and a distributed fuzzy logic control method were adopted to approximate unknown dynamics and drive nonlinear MASs to consensus in [21]. Event-triggered adaptive fuzzy controllers with SMC were employed in [22].One problem of the aforementioned works is that by using the SMC technique, the high-frequency chattering phenomenon was not addressed [23], which causes wear and tear to the actuator and might lead to the possibility of system destabilization. The better solution for alleviating the chattering phenomenon, while maintaining the invariance property of the sliding mode against uncertainties involves the use of high-order SMC [24]-[26]. However, the sliding surface and the adaptive estimation error are shown to be uniformly ultimate bound, and the above designed approaches are based on the dynamical systems with known control directions.
From the above literature, it can be observed that the issues of uncertain dynamics, nonvanishing disturbance, unknown control directions, and the reduction in the chattering for MASs have not been explored all together in a single paper. In this paper we mainly concentrate on the control design of nonaffine agents with a new asymptotically consensus algorithm that can deal with nonlinear dynamics, nonvanishing disturbance, and unknown control directions. As in most of the related works, we first transform the nonaffine agent into the affine dynamics, and then we take its first-order time derivative to raise the order of the dynamics where the derivative of control input for each agent contains affinely.Next, we incorporate the robust integral of the sign of the error (RISE) scheme [27] into the proposed consensus algorithms to cope with the problem of novanishing disturbance in each agent. Furthermore, a mechanism is designed to cope with unknown control directions in each agent. Inspired by the work in [28], the Nussbaum-type function is employed to be included in the RISE scheme.Therefore, in this paper a distributed robust integral of the sign of the error (DRISE) structure is developed, which to the authors’ best knowledge has not been studied, for the highorder nonaffine agents with nonvanishing disturbance. The main contributions of the paper can be summarized as follows:
1) This is the first work to consider the leaderless consensus problem of high-order nonaffine agents with uncertain dynamics, nonvanishing disturbance, and unknown control directions, in contrast to existing results for consensus of nonaffine agents.
2) A new DRISE design combined with the Nussbaum-type function is first proposed to guarantee not only the desired asymptotic consensus, but also the uniform boundedness of all closed-loop variables.
3) Compared to the related literature [16], where the control directions are identical and partially known for agents with undirected graphs, in this work the unknown control directions can be nonidentical for agents with a directed graph having a spanning tree. Furthermore, different from existing results on consensus of agents with nonvanishing disturbance,in this work the integral operation in the proposed control algorithm is adopted to incorporate in a continuous manner and ensure less chattering behavior.
We organize the rest of this study as follows. Preliminaries and problem formulation are described in Section II. In Section III, auxiliary variables and the technical development for open-loop dynamics are presented, and a new control algorithm with the Nussbaum-type function is proposed.Then, the main results on asymptotic consensus are illustrated.Simulation results on Duffing-Holmes chaotic systems are presented in Section IV. Finally, Section V concludes this work with some remarks.
II. PRELIMINARIES AND PROBLEM FORMULATION
Notations:L∞denotes the space of bounded function on[0,∞). |·| represents the absolute value, ‖·‖ represents the Euclidean norm of a vector, and ‖·‖∞represents the infinity norm. The notation sgn (·) is the signum function.
A. Preliminaries
Definition 1 [29]:χ(·) is regarded as the Nussbaum-type function when it has


Definition 2 [30]:The definition of uniformly quasistrongly δ-connected graphs is that for a constantT>0 , the δarcs of G(t) induce a quasi-strongly connected graph in the interval [t,t+T) with anyt≥0.
Remark 2:It is shown [28] that the directed graph having a spanning tree can be regarded as a special case of the uniformly quasi-strongly δ-connected graphs.
Lemma 1 [30]:For a group of single-integrator dynamics,where thei-th one of the dynamics are
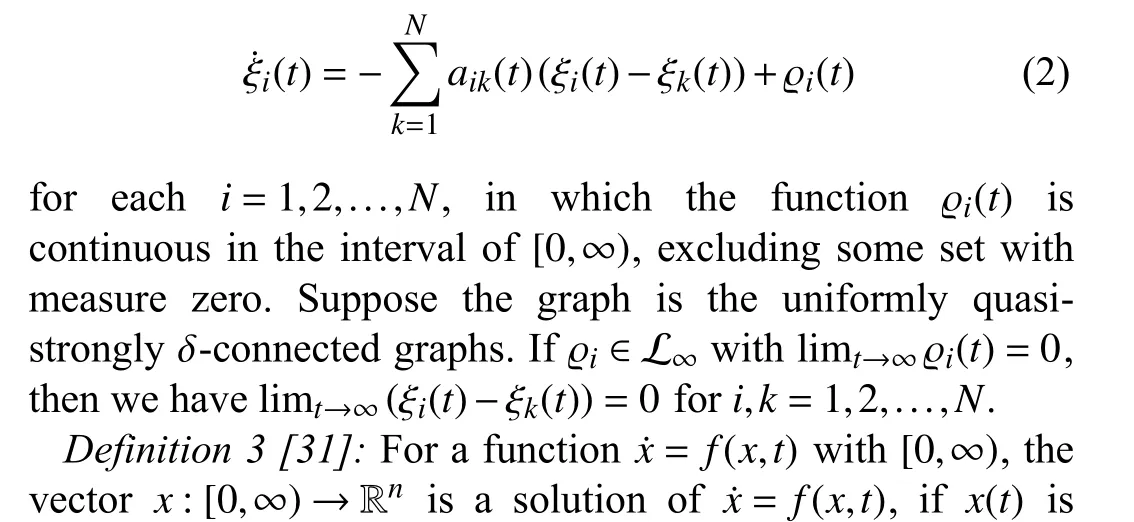

B. Problem Formulation
We considerNnonaffine agents of the form:

The control objective is to design distributed control algorithms for agents (6) under Assumptions 1-3 and communication topology described by directed graphs in order to achieve asymptotic consensus in the sense that

for all agents withm=1,2,...,n-1,i,k∈{1,2,···,N}.Furthermore, all signals of the closed-loop systems are bounded.
III. MAIN RESULTS
A. Auxiliary Variables and the Technical Development
In this subsection, auxiliary variables will be introduced to facilitate the algorithms design, and the technical development for open-loop dynamics will be illustrated. The following lemma will be first introduced to derive the main technical development:



B. Distributed Control Algorithms Design
According to Assumption 2, since the sign of∂f(,ui)/∂uiin (26) is unknown, a Nussbaum-type function should be employed to deal with the unknown control directions. Thus,in this subsection, a new control algorithm with the Nussbaum-type function will be presented to cope with the nonlinear affine dynamics and unknown control directions that achieves asymptotic consensus.
In this subsection, the virtual control inputvi(t) is proposed by

in which each term is available for calculatingpi(t). From(16), (28), and (29), we know that the control inputui(t) can be implemented since all the terms are measurable signals.
In view of (26) and (28), the closed-loop system is


C. Boundedness and Asymptotic Consensus Results
In this subsection, we will prove that if the control algorithms are designed as described in the previous subsections, then all closed-loop variables remain bounded and asymptotic consensus is achieved.
The main result is summarized as follows:
Theorem 1:Suppose Assumptions 1-3 hold. Considering a group ofNnonaffine agents in the form (6) with the proposed control algorithms (28), (29), and (17) under the communication topology described by a directed graph having a spanning tree, all closed-loop variables are uniformly ultimately bounded and semiglobal asymptotic consensus is achieved providing that the following condition is satisfied:

where ςi1and ςi2are two parameters defined in Remark 4.Furthermore, all signals of the closed-loop systems are bounded.
Proof:Let the Lyapunov function candidate be
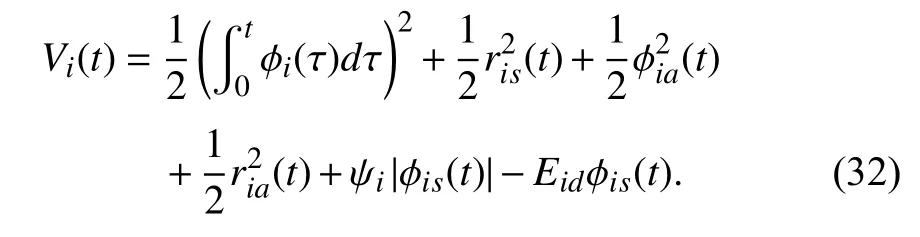
In view of (31) and Remark 4, since ψi>2(ςi1+ςi2)>ςi1,we can obtain that 0 <ψi|φis(t)|-Eidφis(t)≤(ψi+ςi1)|φis(t)|.Thus, it can be proved thatVi(t)>0 is upper bounded as

whereei(t) is defined in Remark 5, andVi(t) is continuous,differentiable everywhere except on the setΦ={ei(t)|φis(t)=0}. Since the Lyapunov function is not directly employed, we use the tool in Lemma 2, that is
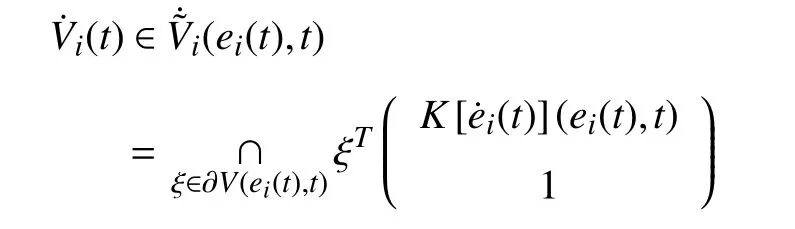
where ∂V(ei(t),t) is defined as
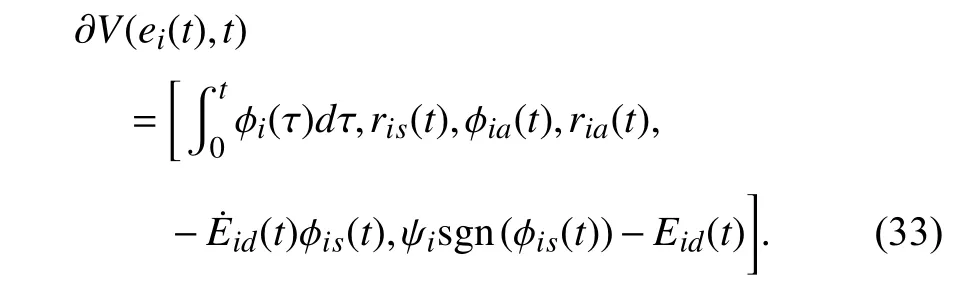
To simplify the analysis, the above ∂V(ei(t),t) can be rewritten as

Therefore, we have



Therefore, the region of attraction can be calculated as

IV. SIMULATION EXAMPLES
In this section, a group of four Duffing-Holmes chaotic systems is considered. The agent model is adopted from [18],and the dynamics of each agent are described as follows:



Fig. 1. The communication graph having a spanning tree.
The simulation results are illustrated in Figs. 2-4. It is observed from Fig. 2 that asymptotic consensus is obtained.Fig. 3 shows the performance of control input. At the beginning of the first 10 s, it is shown that the control input contains some frequent oscillations when the Nussbaum-type function works and the directions of the control inputs are determined. Furthermore, it is seen that the values ofui(t) are within a reasonable range. It is also observed from Fig. 3 that after the first 10 s the chattering phenomenon exists. The reason is that the proposed algorithm in (28) has discontinuous terms, and its integral implies a continuous and chattering control input. As we know, although the control algorithms are smooth, the existence of chattering phenomenon is very common, and the robust control algorithms may be able to eliminate the chattering phenomenon.
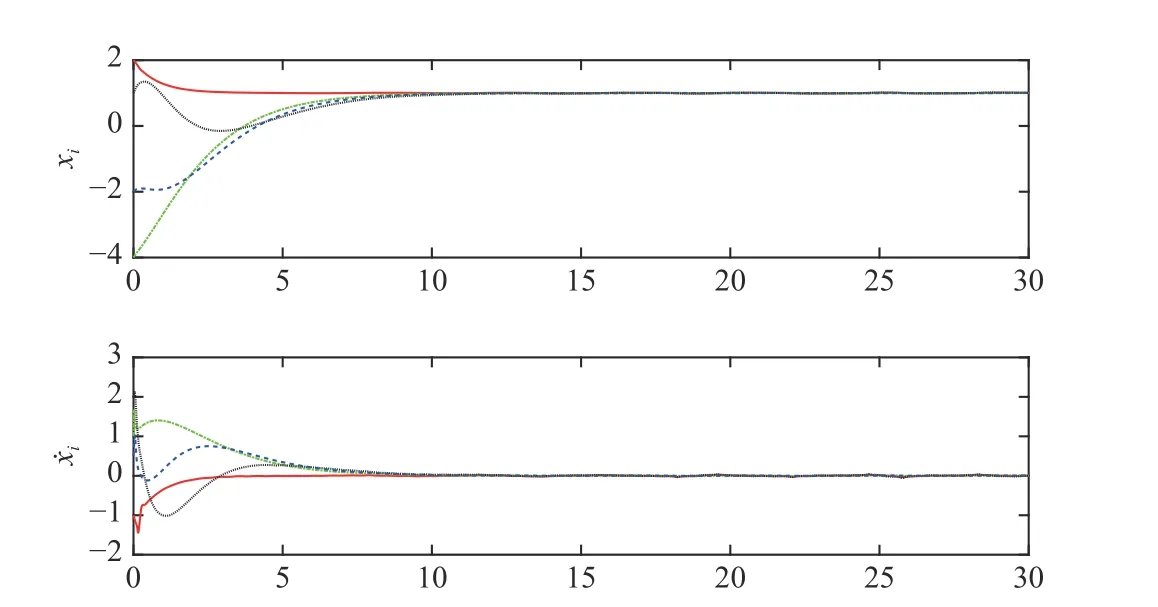
Fig. 2. Time responses of the agent states xi(t) and x˙i(t) (1 ≤i ≤4).

Fig. 3. Time responses of the control inputs u i(t) (1 ≤i ≤4).

Fig. 4. Time responses of the parameters pi(t) (1 ≤i ≤4).
V. CONCLUSIONS
In this paper, we designed asymptotic consensus algorithms for networked nonaffine systems with nonvanishing disturbance under directed graphs. By using the DRISE design with the Nussbaum-type function, a new class of continuous algorithms with disturbance rejection has been developed. The corresponding asymptotic consensus results relax the chattering phenomenon since the proposed control algorithms are continuous. Future research directions may focus on designs of algorithms for output feedback systems, eventtriggered control systems, and time-delay systems.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Speed and Accuracy Tradeoff for LiDAR Data Based Road Boundary Detection
- Finite-Time Fuzzy Sliding Mode Control for Nonlinear Descriptor Systems
- A Novel Rolling Bearing Vibration Impulsive Signals Detection Approach Based on Dictionary Learning
- Dual-Objective Mixed Integer Linear Program and Memetic Algorithm for an Industrial Group Scheduling Problem
- Output-Feedback Based Simplified Optimized Backstepping Control for Strict-Feedback Systems with Input and State Constraints
- Empirical Research on the Application of a Structure-Based Software Reliability Model
