Empirical Research on the Application of a Structure-Based Software Reliability Model

Jie Zhang, Yang Lu, Ke Shi, and Chong Xu

Abstract—Reliability engineering implemented early in the development process has a significant impact on improving software quality. It can assist in the design of architecture and guide later testing, which is beyond the scope of traditional reliability analysis methods. Structural reliability models work for this, but most of them remain tested in only simulation case studies due to lack of actual data. Here we use software metrics for reliability modeling which are collected from source codes of post versions. Through the proposed strategy, redundant metric elements are filtered out and the rest are aggregated to represent the module reliability. We further propose a framework to automatically apply the module value and calculate overall reliability by introducing formal methods. The experimental results from an actual project show that reliability analysis at the design and development stage can be close to the validity of analysis at the test stage through reasonable application of metric data. The study also demonstrates that the proposed methods have good applicability.

I. INTRODUCTION

THE essence of software reliability engineering lies in improving software quality, and its role covers all development stages. Most software reliability studies use failure data from the test stage, which focuses on predicting the relatively stable interval of the reliability growth curve and providing the basis for adjustment of test workload and software release strategy. Recent research suggests that reliability evaluation in the early stages has important implications for avoiding possible revision costs in the middle and later stages of development, especially for reliabilitysensitive and safety-critical software systems [1]-[4].Generally, in order to optimize software design, appropriate methods can be introduced as early as possible to evaluate the overall reliability of different architectures. Structural reliability modeling works for this, which takes a component as a basic granularity and considers interaction modes and structural styles of component compositions. Typical models include semi-Markov process (SMP) [5], discrete time Markov chain (DTMC) [6], and continuous-time Markov chain (CTMC) [7]. Compared with the traditional reliability models such as Goel-Okumoto (G-O) [8], they belong to a Markovian model which is based on a stochastic modeling method.

Markovian models will be state-explosion-prone when used in large-scale and complex software. As such, state-free models are also used to evaluate software system recently.Zhenget al. [9] present an analytical approach based on Pareto distribution for performance estimation of unreliable infrastructure-as-a-service (IaaS) clouds. Liet al. [10] employ an autoregressive moving average model in time series for quality-of-service (QoS) prediction of real composite services.The above method considers the dynamic change in continuous runtime, but does not focus on the static analysis of component structure. Xiaet al. [11] use a stochastic-Petrinet to calculate the process-normal-completion probability as the reliability estimate since Petri-nets are highly capable of describing complex component-based software. However, this study still needs experimental data and is not suitable for software reliability evaluation at early design stage. In contrast, the structural model represented by DTMC is more suitable for a reliability assessment at this stage, because it usually does not require runtime data.

Stochastic modeling is limited in practical applications of structure-based software reliability analysis. Take the DTMC model as an example. Its two key parameters required for modeling, component reliability and control transfer probability among components, are given by simulated cases rather than from actual projects [12]. Consensus of previous research is that a single component can be regarded as a black-box, and the component parameters tend to be stable in continuous reuse and iteration. But reliability cannot be the inherent property of software components because of the difference in requirements and external environments between actual projects. Moreover, the state explosion caused by component-level modeling is also a difficult problem in the application of large-scale complex software. Recently, more attention was paid to service/cloud-based software reliability.Xiaet al. [13] present a stochastic model based on a Poisson arrival process for quality evaluation of IaaS clouds. This work considers expected request completion time, rejection probability, and system overhead rate as key metrics, and can be used to help design and optimize cloud systems. Luoet al.[14] propose a scheme to build the ensemble of matrixfactorization based QoS estimators and achieve an AdaBoostbased aggregation result. This work presents high estimation accuracy at low time cost. Furthermore, the authors incorporate second-order solvers into a latent-factor based QoS predictor which can achieve higher prediction accuracy for industrial applications [15]. The above studies come from actual QoS data and emphasize the role of different measure factors in software performance analysis and prediction. When conducting a structural reliability analysis of a software project, an important revelation is whether the actual software metrics data can be effectively used. In order to avoid state explosion, the trade-off of module granularity should be based on actual project scale and difficulty of obtaining metrics.

Recent reliability empirical studies most use traditional software-reliability-growth-models (SRGMs) which focus on failure data from the test stage. Luan and Huang [16] present a Pareto distribution of faults in large-scale open source projects for better prediction fitting curve. Sukhwaniet al. [17] apply SRGMs to NASA’s SpaceFlight software to analysis of relevant experience information in the software development process and version management. Aversano and Tortorella[18] propose a reliability evaluation framework for free/open source projects. It was applied to evaluate quality of an open source ERP (enterprise resource planning) software based on a project bug report. Hondaet al. [19] discuss the effect of two types of measurement units — hourly time and calendar time — in reliability prediction of industrial software systems.Tamura and Yamada [20] present a hierarchical Bayesian model based on fault detection rate around a series of open source solutions and address the impact of conflict behavior of components when dealing with system reliability. This work considers structural information at the component-level, but only takes into account the noise caused by these conflicts in the early stage of the fault detection curve due to the missing discussion of the structural analysis.

The above works cannot be employed in the early stage of development since they require failure data obtained from software tests. Failure data can be attributed to the scope of software metrics. Besides, another type of software metrics has been applied to reliability analysis and defect prediction of actual projects. Complexity measurement data, which has low collection cost, can also be utilized in cognitive modeling[21]. Shibataet al. [22] combine a cumulative discrete-rate risk model with time-related measurement data, and prove that the new model is equivalent to a generalized fault detection process whose goodness of fit and predictive performance are better than the popular NHPP SRGMs. Kushwaha and Misra[23] consider the importance of the cognitive measure of complexity and use it in a more reliable software development process. Chu and Xu [24] present a general functional relationship between complexity metrics and software failure rate, which can be used to predict reliability on exponential SRGMs. Bharathi and Selvarani [25] calculate the reliability influence factors separately for several object-oriented design metrics, and finally, deduce the reliability formula of the class-level granularity by merging these factors through an aggregation strategy. This work is a beneficial trial for evaluating software reliability during the design phase.D’Ambroset al. [26] compare the performance of several software defect prediction methods and explain the factors of threat validity in practical applications. This work is generally based on static source code metrics and dynamic evolution metrics. Zhanget al. [27] group existing defect prediction models based on software metrics into four categories.Through verification of a large number of open source projects, they describe how to aggregate these metrics in order to achieve a significant effect on predictive performance and recommend the simple and efficient aggregation scheme of summation.

However, measurement and SRGM-based empirical studies have several limitations: 1) they cannot calculate the reliability in the early design stage of software system; 2) they are not structure-based methods, and cannot assist in architecture design and optimization. Markovian models such as DTMC can work for this, but they usually have great difficulty in practical application due to lack of real data. We have seen the combination of software metrics with traditional reliability models and detect-prediction methods [22], [24],[25]. We aim to incorporate software metrics into early modeling for software reliability in order to effectively quantify system performance. Our empirical study focuses on the following two research questions:

RQ1:From the perspective of early reliability analysis, what kind of structure granularity is appropriate and how does one use software metrics?

RQ2:How does one evaluate overall system reliability in practical engineering?

The remainder of this paper is organized as follows. Section II introduces the reliability model DTMC and the formal method we used for model construction and calculation. Section III describes the experimental methods of this paper, including object selection, metric data processing and aggregation. The results of this study are presented in Section IV. We evaluate the performance of our approach against other models in Section V, and discuss the threats to validity of our work in Section VI. Conclusions are drawn and future work is described in Section VII.

II. RELATED WORK

In this section, we introduce the typical early reliability model first, and then present the method we utilized to apply the model.

A. Structure-Based Reliability Model

In the early stage of software development, the traditional reliability model is not available due to lack of failure data. A class of structure-based models work for this [1]-[3]. The most popular one is the DTMC (discrete time Markov chain)model [6]. Here is an example of the ESA’s (European space agency) control system software [28]. It contains four main components (N1toN4), and the control transfer between components as shown in Fig. 1.

Correspondingly, we have a one-step stochastic transfer matrix as follows:

Fig. 1. The ESA software architecture.

The entryQi,jrepresents the transition probability from stateitojin the Markov process. Here,Qi,j=R1P1,2, reflects the probability that the system execution state is transferred fromN1toN2in one step, which equals to the product of reliabilityR1and the transfer probabilityP1,2.R1expresses the probability of executingN1successfully. Each componentNimay fail with the probability 1-Ri, and each component failure causes system failure. This is a failure independent hypothesis for this model.

The powerQnof the matrixQis defined as ann-step stochastic transfer matrix whose entryQi,jnreflects the transition probability from stateitojinnsteps. The Neumann series of matrixQis

whereIis the identity matrix. LetN1be the starting module andN4the ending module. The entryS1,4in matrixSdescribes the transition probability fromN1toN4through all possible steps. Then the system reliability can be expressed as the probability of successfully reachingN4and successfully executingN4, which can be calculated by

This model emphasizes the influence of structural changes on overall reliability from the perspective of control flow.Subsequent improvements have been proposed on this basis.

B. Algebraic Method

The DTMC model is built around the control transfer relationship between components. However, the reality is that designers seldom use it to represent the system architecture,and module developers only generate control flow graphs at the method-level. For this we have provided an easy-to-use method in our previous studies [29]. In general, we use an algebraic paradigm instead of graphical expression for higher abstraction. The transfer relationshipN1→N2in Fig. 1 is expressed asN1⊕N2, where the operator ⊕ denotes that the basic control transfers between components are motivated[30]. So Fig. 1 can be expressed as a set as follows:

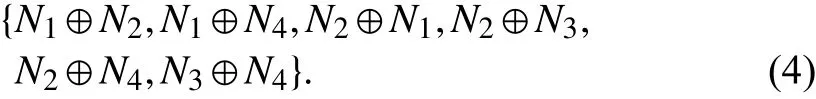
This solves the problem that where the system structure is too complicated for graphic expressions. Especially, when components are designed as a coupling substructure, such as parallel, it is naturally solved by adding an operator in algebra.We can even express the nesting of structures by bracketing them.

We propose a parser which left-to-right scan and rightmost derivate (LR) each expression in the collection as above. The following functions are used in the parser algorithm:

where C is a collection of components, S is a collection of state nodes. This series offˆ for different algebraic expressions are used to generate system state nodes which contains reliability attributes, and mark them on the transition matrixQ. The elements in the matrix are constantly updated in the scan. When the scan is complete, the matrix can be directly applied to (2).

This formal method can be easily instrumentalized to facilitate engineers. In the simulation study, it performed well.We summarize the above method as a process framework, as shown in Fig. 2.

Fig. 2. A framework for automatically applying DTMC.

III. EXPERIMENTAL DESIGN

Properties of the research object and its experimental data are explained in detail. Some methods are applied to reasonably preprocess and aggregate metric data. And the improved framework is used to calculate the overall reliability.

A. Research Object

We select the open source project jEdit [31] as the research object. jEdit is a mature programmer’s text editor with hundreds of person-years of development behind it. It is written in Java and runs on any operating system with Java support. This project is in proper scale, and it is representative for development technology.

The current version is set as jEdit 4.3. It is because that the metric data of jEdit in the PROMISE repository [32] contains version 3.2.1 to version 4.3. Although version 4.3 is not the last stable version, it does not affect the universal property of this study since there is no fundamental change in higher versions. We consider ourselves as developers and designers,so we can get the necessary information of structure from thedesign document or source code. This information includes packages, files, and classes, as listed in Table I.

TABLE I THE STRUCTURAL INFORMATION OF JEDIT 4.3

Here we define the granularity of structural module analysis at the package-level, and the corresponding level can be found in other language environments. It needs to be based on the previous version when we are seeking detailed module information at the design stage. It usually works because of the limited changes in modules between versions. As the coding continues, we can continuously adjust the changes to the files and classes of the modules. The final structure information of version 4.3 is as described in Table I, and the metrics are based on this.

B. Metric Data Processing

The PROMISE library includes nearly thirty metrics for jEdit. We use three main categories— traditional metrics,object-oriented (OO) metrics, and process metrics — to describe the metric data. The data are summarized at the method-level, class-level and file-level respectively [33], and the developer can easily collect them via the specified tools.At the method-level, the number of lines of code (LOC) and the cyclomatic complexity (CC) [34] are still suitable for code analysis inside a class, which existed before object-oriented programming appeared. The CK set [35] has a wide range of applications, but there are also metrics that emphasize perspectives such as encapsulation, coupling, etc. [36]. The eight metrics recommended by Moseret al. [37] have typical process characteristics, and are further improved in the MJ set [38].

Simple data sampling is not used in this paper. For early reliability analysis, the initial metric data needs to be cleaned to highlight the structural characteristics of the metric elements. We use the following method:

1) The process metric elements (from Moser and MJ set) do not apply to static analysis for the target version. This work only uses traditional metrics and OO metrics.

2) The remaining 20 metrics are divided into five categories: complexity, coupling, cohesion, inheritance and size. We use Spearman’s coefficient [39] to measure correlation in 5 subsets. The data is not required to follow any particular distribution in the state of Spearman correlation,and it ranges from -1 to +1 where a larger absolute value indicates the stronger correlation. Table II shows the calculation results (e.g., the coupling metrics).

Absolute values of more than 0.5 have relevance and values of more than 0.8 have high correlation. Observe that there are redundant metrics that can be removed to further simplify calculations. According to the CFS algorithm of attribute selection [40], one metric with relatively high relevance is

TABLE II CORRELATION OF THE COUPLING METRICS

selected as a main feature in each category. The maximum cyclomatic-complexity (MAX_CC), coupling between object classes (CBO), cohesion among methods (CAM), depth of inheritance tree (DIT), and response for a class (RFC) are finally selected elements as representative for the five categories separately. It ensures that subsequent calculations which can characterize 5 different characteristics instead of examining correlations across all metrics. Table III lists the data we actually used in this research when deal with the browser module in Table I.

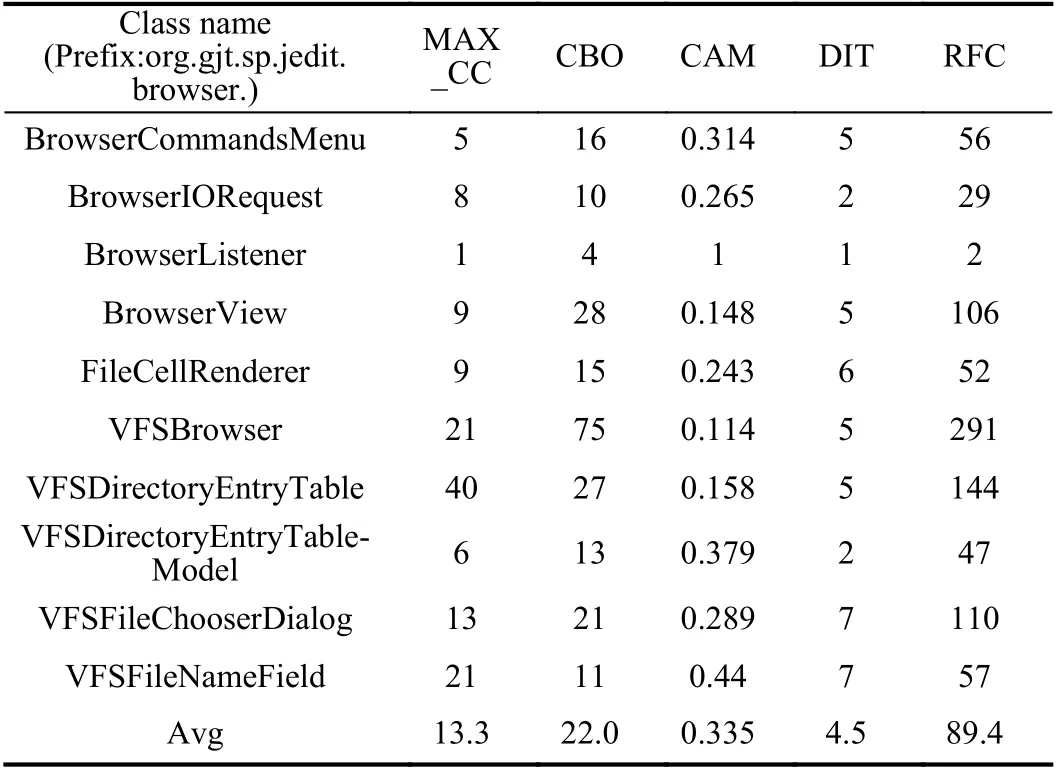
TABLE III THE METRIC DATA USED IN THIS RESEARCH

C. Aggregation Scheme

The metric data are only collected at the class-level. It is necessary to propose a descriptive scheme to aggregate the final value of software system reliability. We suggest a twostep frame and the details are presented as follows.

Step 1:To establish a functional relationship between metrics and degree of reliability in order to calculate module reliability value.

We define the degree of reliability influence, which is similar to the definition in [25]. LetRImirepresent influence of the metric scalarmi. It is calculated by

wheredpcindicates the number of defect prone classes atmi,andmcindicates the number of classes contained in one module. Notice thatRIis only calculated in one module, since the coding style of each module may not be consistent. The range of scalarmiincludes all samples of the specified metric element. Table IV listsmi,dpc, andRImiof 5 metric elements in the module browser, whenmc= 10.

It is observed from Table IV thatdpcis counted for eachmiper elements, and eachmivalue is a sample of the metric space. The counting method ofdpcis summarized as: If the class, which is associated with the specific value ofmiat one metric element, a) is submitted with a bug in the previous version,dpc←dpc+ 1; b) or is newly developed andmiexceeds threshold,dpc←dpc+ 1.

The thresholds of RFC(222), CBO(24), and DIT(6) refer to the NASA standard [41]. The threshold of CC(15) is derived from [34], and the threshold of CAM(0.50) comes from [38].

In general, lower metric value means higher reliability. But it cannot be concluded that there is a linear correlation between metric value and reliability influence. We use polynomial regression to estimate the relationship between the two, because of changes of software reliability mostly in the form of curves. As an example, the functional estimation equations of the browser module are

wherea,b,c,d,eare the independent variables in each fitting function. According to the average value of metrics listed in Table IV, the five degree of reliability influence in the browser module can be calculated as:RIRFC(89.4) = 90.941,RIMAX_CC(13.3) = 91.330,RICAM(0.335) = 96.414,RICBO(22.0) = 92.744,RIDIT(4.5) = 78.600.

Aggregation strategy can significantly alter correlations between software metrics and the defect count. Zhanget al.[27] indicate that the summation strategy can often achieve the best performance when constructing models predict defect rank or count. Although the perspectives of defect prediction and reliability evaluation are different, they are effectively the same in terms of the use of metrics. The difference is that the former focuses on the situation after the current version, and the latter focuses on the current developing version.Therefore, in this paper, we use the summation strategy to calculate the reliability degree of the individual module according to the reliability influence of each factor. It is calculated as

whereriis weight of theith metric element. Since the five metrics used in this paper are pre-screened to represent a logical category, they are considered equally important. Letri= 1/n= 1/5, where reliability of the browser module is 90.006(%) after the weighted summation.

Step 2:To establish the structural reliability model according toRmodule.

In the software design and development phase, reliability engineering often needs to be carried out by architects andcoders. The module developer calculatesRmoduleby counting the related metrics. One can gather this information of all modules to aggregate into system reliability.

TABLE IV THE RI STATISTICS IN THE BROWSER MODULE

Here we use the formal method presented in Section II-B to establish the DTMC reliability model quickly and accurately.The method is based on algebraic expressions, which can accurately express the control transfer between modules instead of using graphical representation. In addition to the value ofRmodule, module developers are required to submit related expressions based on their understanding of the business. For the browser module (N1), the developers need to submit:

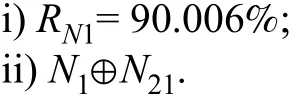
Note that the expressionN1⊕N21replaces the directed arc of graph to describe the control transfer relationship betweenN1andN21. It indicates that further processing of the file system will go to the utility module (N21).

A module developer can separately submit expressions that confirm design intent, which formally starts with the developing module and links all possible next modules in the control flow. In some cases, architects can also submit or modify expressions based on overall understanding. As a description of the structure, algebraic expressions are precise and unambiguous. They are lightweight and easy to use for engineers. One can do this at the same time as designing and coding, without any distractions in describing the whole system.

Eventually, an expression set can be collected which contains two key parameters required for the DTMC model —RiandPij.Ricomes from the submitted information which is usually attached to a concrete expression. Transfer probabilityPij, which is indicated byNi⊕Nj, is equally divided by all possible transfers from moduleNi. The LR parser presented in Section II-B can calculatePijautomatically during scanning.

Finally, as an improvement to Fig. 2, the new framework is proposed as Fig. 3.

Fig. 3. The improved framework for empirical research.

IV. RESULTS

This section provides our experimental results. We focus on findings from actual application of methods in Section III, and answer the research questions presented in Section I.

RQ1:How to determine the appropriate structure granularity in order to apply the corresponding metrics to reliability analysis?

In general, software design has the characteristics of modularization, which is advantageous to the maintenance of projects and the deployment of resources. Early reliability analysis can only start with the structure of the software system. The structural characteristics are represented by the relationships between modules. This requires selecting the appropriate module granularity. In this paper, we suggest that Java OO projects should be analyzed at the package-level. The corresponding granularity of other types of OO projects can be found in the directory structure and design documents.

Table I lists the module division of jEdit. Some modules of version 4.3 do not exist in previous versions, and some have changed in later versions. However, analysis at the packagelevel can cover all relevant metrics collected at the method- or class-level. Different packages show significant differences in metrics due to the diversity of functionality and developer. We randomly choose eight out of 23 modules, and present boxplots of them under the five selected metrics. As shown in Fig. 4, the distributions of metric data are obviously different,and most of them are different from the entire distribution. It shows that the coding style of each module is different, i.e.,the quality of each module in the same software is also different. Furthermore, the life cycle and application scope of many components (packages in java projects) goes beyond the project itself. E.g., “util” and “xml”, which are independent of jEdit’s main business, came from or could be used for other projects. Therefore, we think that for each different module,the reliability influence from its metric data should be analyzed separately. And then the reliability data of all modules should be integrated with a specific structural analysis method.

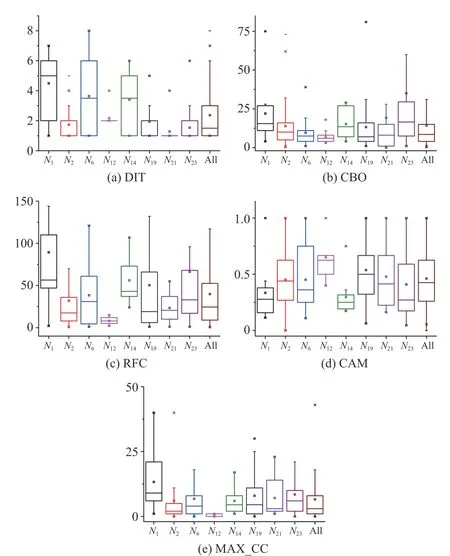
Fig. 4. Boxplots of 5 metric values resourced from eight modules and whole.

RQ2:How to evaluate the reliability of a software?

We calculate the reliability value of a single module based on (6) and (8). Table V lists the reliability degree for all modules in 4 versions of the jEdit project. Note that version 4.3 is the last version in PROMISE repository, and it is also the one set for the current review. The first version 3.2.1 is discarded because we need to trace back a version for countingdpcin (6).

Fig. 5 presents the boxplots of the numerical results in Table V.It shows that statistically, the overall distribution gradually increases as the version changes. It can be seen from the diagram that most module reliability values increase as the version changes. This is in line with the expectation that the module quality will improve as more bugs are fixed. From the perspective of structural analysis, we still want to estimate a specific value to reflect the overall reliability of software.

With version 4.3 as the goal, module developers should present the relationship between this module and other modules in addition toRmodule, which can be described conveniently by algebraic expressions. Then, the expression set of {N12⊕N3,N12⊕N6,N12⊕N19, …} can be collected.ExpressionN23⊕Cshould be added into the collection in order to facilitate model calculation, which means the requirement of business termination is only initiated by the core moduleN23.Cis the ending node and its reliability value is 100%. Thestarting module isN12, which means that the message occurs when the business is coming.

TABLE V THE RMODULE VALUES IN DIFFERENT VERSIONS OF JEDIT

Fig. 5. Boxplot of reliability degree in all modules among four versions.

We also set up an expression set for three other versions,and use the Fig. 3 framework to automate the overall software reliability calculation. Fig. 6 shows the results. To illustrate the effectiveness of the proposed method, two traditional growth models: the classical G-O model [8] and Huang’s testeffort model [42] are used as comparisons. In this work, we follow the common practice in empirical research of SRGMs[16]-[19], where the failure data is extracted from the bug reports. This is under basis of the following assumptions: 1)Confirmed bugs cause failures; 2) Each failure is independent;3) Fixing bugs will not introduce new bugs. According to the reports obtained from the official website of jEdit [31],version 4.0 has 226 closed bugs within 215 days since the previous release. The G-O model use a statistical process based on this failure intensity, and the prediction result at the release time of jEdit 4.0 is 88.736%. Version 4.1 has 167 closed bugs within 407 days, and the prediction result is 89.413%. The data for versions 4.2 and 4.3 show that there are 106 bugs within 557 days and 12 bugs within 1848 days. The prediction results are 92.185% and 96.587%,respectively.Furthermore, as suggested in [42], the cumulative interval is used here as the test-effort which is available from the detailed entry of each bug in the report. The prediction results of Huang model across the four versions are 90.156%, 91.142%,92.868% and 96.224%, respectively.

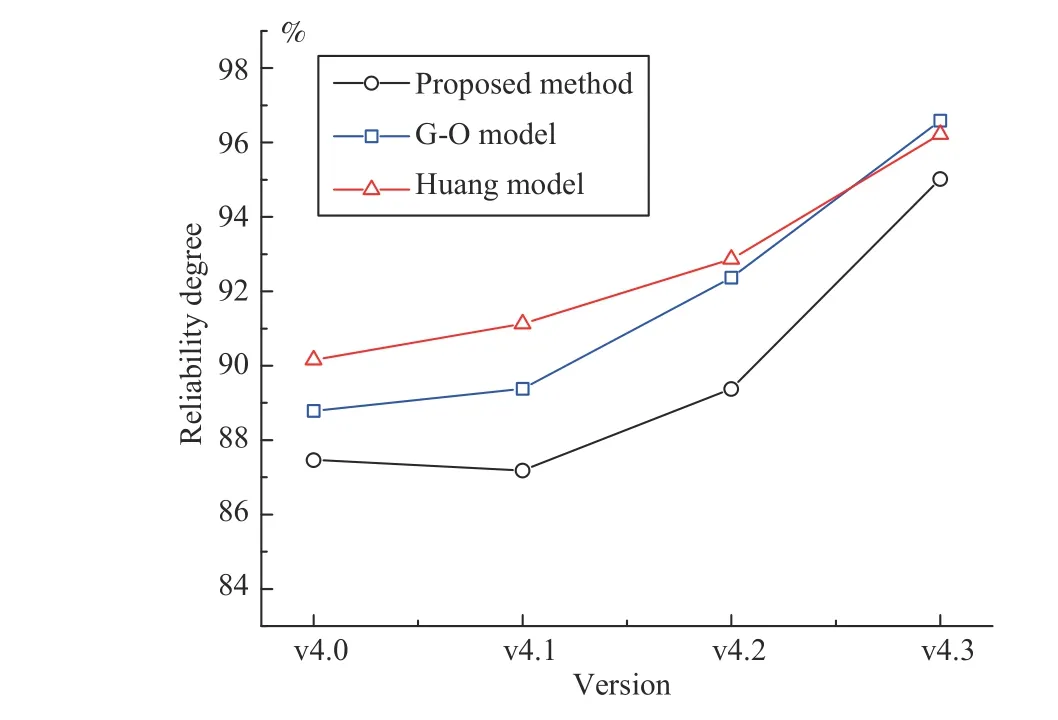
Fig. 6. Reliability trends on four versions of jEdit.

V. DISCUSSION

A. Characteristics of Early Reliability Modeling

Unlike SRGMs, early reliability modeling only relies on structural analysis of software system. As mentioned in the first section, the modeling parameters come from a single software module and the relationship between modules.Therefore, it is meaningless to compare the predictive performance with a class of models based on failure data.Most reliability-prediction models, such as SRGMs, are utilized to optimize the release strategy to achieve a balance between quality and test costs. But the significance of the early model is to optimize the structure and guide the test.

We show the trend of changes in the results of the proposed method in Fig. 6, and also use two representative models to illustrate the correctness. It should be explained that the calculation of each version of this method can be performed at the design stage. And based on the framework in Section IIIC, the calculation process is automatically complemented by tools. This means that the reliability evaluation can be carried out at any time with structural design changes. It helps decrease the difficulty of applying the structural reliability model into practice.

As shown in Fig. 6, the numerical values evaluated by the proposed method (87.267%, 87.184%, 89.381%, 94.223%)are lower than by the traditional models. This is because calculations based on metric data can magnify the impact of defect-prone classes. For the calculation of defect tendency,the method of this paper tends to be conservative.Correspondingly, the SRGMs which are based only on test data assume that the reliability curve increases with bugs fixing. Their evaluations are relatively optimistic in general.

B. Sensitivity Analysis

The influence of software local structure on reliability can be analyzed through sensitivity. This effect can only be manifested in the computation of the structural reliability model. As shown here jEdit 4.0 is upgraded to 4.1. The result,which differs from the traditional models’, appears to be slightly reduced. By partially fixing pre-existing defects, new versions can also have reduced reliability with the introduction of new modules and features (such asN7in jEdit 4.1).

We use the criticality to analyze sensitivity. It is computed by the following formula:

where ΔRiis the reliability increment of moduleNi, ΔRsysis the overall reliability increase corresponding to this increment.In fact, when the ΔRiis very small, we useCiinstead of the partial derivative, i.e., the criticality of moduleNiis an approximate value of the module sensitivity. However, in terms of computational complexity, computing criticality is much better than computing sensitivity. The sensitivity(partial derivative) onRican only be solved based on cofactor expansion, which leads to a geometric increase in computational time and space when the total number of modules grows. In contrast, (9) can be calculated automatically by the proposed framework in Fig. 3.

For jEdit 4.3, we set a small negative increment of 0.005 for all module reliability. Fig. 7 shows theCicorresponding to each change of ΔRi. It can be seen that the reliability sensitivity of core moduleN23and message moduleN12are significantly higher than others. This conforms to the expectation of actual control flow at design stage. And this means that later testing on such modules will help significantly improve the overall reliability of software.However, some modules (such asN18) are not considered to be the important nodes in structure because they only interact with very few modules. These may not be the goals that reliability engineering needs to focus on.

VI. THREATS TO VALIDITY

1)Project Selection:In this work, the open source project jEdit is selected. In addition to using metrics, we need to analyze the software structure and apply a complex evaluation framework. We only discussed one project because of space constraints.

Fig. 7. Analysis of reliability sensitivity of modules in jEdit 4.3.

The threat to our treatment mainly arises from applicability of our method on other OO projects. Metric data can be obtained from public repositories, but also can be directly calculated from the source code. Structural information can be analyzed from design documents and source codes. We believe that the applicability of the proposed method is not a problem. Furthermore, it is recommended that non-java projects should be tested using our approach and the results may be slightly different.

2) Metrics and Techniques Selection:These metrics and its classification we used are popular and commonly investigated in defect prediction literature. With the same kind of metrics,correlation analysis technique is used to eliminate redundant impacts. A study on more correlation analysis techniques is required. In addition, the DTMC model used in this paper is the most important structural analysis model at present. The proposed framework uses formal techniques to show the application of this model. Formal techniques have been fully elaborated and verified in our previous studies. We will provide an open-source implementation of analytical algorithms online. Replication studies using different early reliability models, such as CTMC, to utilize this framework and may prove fruitful.

VII. CONCLUSION

Although there are many practical difficulties in reliability analysis and evaluation of software projects in early development, the calculation results from the reliability model can provide reference for the optimization of software architecture design. By analyzing the software structure, we find the sensitive modules that affect the overall reliability,which provides a practical basis for subsequent reliability distribution and stress testing. Theoretical research of structure-based software reliability models has been studied extensively, but the biggest obstacle to its further development is determining how to apply it to practical projects.

Our main work is to provide a complete solution for early reliability evaluation. We first give a method for processing metric data and aggregating it into module reliability. Then we propose a process framework, which automatically calculates the overall reliability value based on module parameters and expression forms. Using a series of different methods, our research shows the implementation of a structural reliability model in practical projects. Evaluation of an OO project shows that we can get an approximating result vs. traditional models which are based on software failure data. It provides new ideas and methods for the empirical research of reliability.

The work is original and operable in the selection and aggregation of software metric data and the practice of structural analysis model. The next steps of research will be continued in two areas:

1) Consider establishing a functional relationship between metrics and reliability on more metric elements. The fitting method of the function is not limited to one but also, selects the appropriate method according to different modules and developers, such as Stepwise Regression and Ridge Regression.

2) Defect prediction Technology continues to show new results. In addition to the traditional methods, a method using random neural networks (RNN) has recently been proposed,and the results are good. This prediction model is established on the time axis and describes the evolution of each software module. We will consider the use of better-performing solutions in the prediction of defect-prone classes to improve the reliability evaluation of modules.