Finite-Time Fuzzy Sliding Mode Control for Nonlinear Descriptor Systems

2021-06-18ZhixiongZhongXingyiWangandHakKeungLam

IEEE/CAA Journal of Automatica Sinica 2021年6期

Zhixiong Zhong,, Xingyi Wang, and Hak-Keung Lam,

Abstract—This article addresses the finite-time boundedness(FTB) problem for nonlinear descriptor systems. Firstly, the nonlinear descriptor system is represented by the Takagi-Sugeno(T-S) model, where fuzzy representation is assumed to be appearing not only in both the state and input matrices but also in the derivative matrix. By using a descriptor redundancy approach, the fuzzy representation in the derivative matrix is reformulated into a linear one. Then, we introduce a fuzzy sliding mode control (FSMC) law, which ensures the finite-time boundedness (FTB) of closed-loop fuzzy control systems over the reaching phase and sliding motion phase. Moreover, by further employing the descriptor redundancy representation, the sufficient condition for designing FSMC law, which ensures the FTB of the closed-loop control systems over the entire finite-time interval, is derived in terms of linear matrix inequalities (LMIs).Finally, a simulation study with control of a photovoltaic (PV)nonlinear system is given to show the effectiveness of the proposed method.

I. INTRODUCTION

THE fuzzy control algorithm consists of a set of fuzzy logic, fuzzy sets, and heuristic control rules [1]-[3], and it has been used for the effective handling of control of complex nonlinear systems including robotic teleoperations [4],surgical robotics [5], and multiple robots [6]. Among these fuzzy control methods, Takagi-Sugeno (T-S) fuzzy model uses linear equations to represent each local system corresponding to their local rules, and then employs fuzzy reasoning to blend local linearity for implementing total nonlinearity. Nowadays, the T-S model has been very popular in the control society because of its ability to provide good approximation. Therefore, over the past few decades, the problems of stability analysis and control synthesis have been investigated for the T-S fuzzy model more frequently [7]-[9].

Sliding mode control (SMC) has been regarded as one of the most powerful nonlinear control methods, and has been widely used due to its quick response and strong robustness in practical applications. The essence of SMC is to drive state trajectories toward the switching manifold. Such motion is motivated by imposing disruptive control actions, commonly in the form of switching control strategies. An ideal sliding mode exists only when the system state satisfies the dynamic equation that governs the sliding mode for all time. This requires an infinite switching, in general, to ensure the sliding motion. The past decades have witnessed the successfully practical application of SMC in several areas (see [10]-[13]).In addition, descriptor systems are referred to as implicit/singular systems, which enable describing a larger class of systems than the normal model representation [14].More recently, stability results of fuzzy descriptor systems using the SMC method have been reported in [15]-[17].However, note that the aforementioned works only highlighted the asymptotic behavior of the fuzzy control system over an infinite working time interval, and all aforementioned works of the SMC consider system dynamics within a sufficiently long time interval. In fact, in many practical applications, a finite-time stability (FTS) may be required when facing the prescribed restraints on transient dynamics, such as, for example, dual-arm robots [18], [19],input-delay systems [20], Markovian jump cyber-physical systems [21], multi-input and multi-output (MIMO) nonlinear systems [22], [23], and nonlinear systems with positive powers of odd rational numbers [24]. Both FTS and practical stability (PS) have a similar definition for stability analysis,and they work on the boundary of state trajectories starting from a desired initial region. However, the main distinction between FTS and PS is that FTS works with a finite period while PS works for an infinite amount of time [25]. When taking into account norm bounded disturbances, the concept should be changed from FTS to finite time boundedness(FTB). FTB ensures FTS, but its converse is not true [26]. We are aware that the finite-time SMC of fuzzy descriptor systems is of the wide practical applicability. However, few works studied the FTB of the FSMC descriptor system in both the reaching phase and the sliding one. It reflects the following two important control problems. One is determining how to partition the specified finite timeSinto two subintervals [0,S*] and [S*,S], which ensures the FTB of the corresponding FSMC descriptor system over the reaching phase and sliding motion phase. The other is determining how to design the FSMC law via linear matrix inequalities (LMIs),which ensure the FTB of the closed-loop fuzzy descriptor system over the whole finite-time interval [ 0,S].

Motivated by the aforementioned considerations, this paper proposes a novel fuzzy sliding mode control strategy for nonlinear descriptor systems using a FTB method. Firstly, the nonlinear descriptor system is represented by the T-S model,where fuzzy representation is assumed to be appearing not only in both the state and input matrices but also in the derivative matrix, and the derivative matrix is assumed to not always be nonsingular. By using a descriptor redundancy formulation, the fuzzy representation in the derivative matrix is reformulated into one that is linear. Then, we introduce the fuzzy sliding mode control (FSMC) law, which ensures the FTB of the closed-loop fuzzy control systems through the reaching phase and sliding motion phase. Moreover, by employing the descriptor redundancy reformulation, it is shown that a sufficient condition for designing FSMC law,which ensures the FTB of the closed-loop control systems through the entire finite-time interval, is derived in terms of LMIs. Finally, a simulation study for the control of the photovoltaic (PV) nonlinear system is provided to show the effectiveness of the proposed method. The main contributions of this paper are summarized as follows: 1) For a specified time interval [ 0,S], we partition it into two subintervals [0,S*]and [S*,S], where the proposed FSMC law ensures the FTB of the corresponding FSMC descriptor system over reaching phase and sliding motion phase. 2) Sufficient conditions for designing the proposed FSMC law, which ensures the FTB of the fuzzy descriptor system over the whole finite-time interval[0,S], are derived in terms of LMIs.

II. PROBLEM FORMULATION AND PRELIMINARIES

Descriptor systems are referred to as implicit/singular systems, which enables us to describe a larger class of systems with normal model representation [14]. This paper considers a class of nonlinear descriptor systems Currently, the most attention is given to nonlinear systems with “sector nonlinearities” [8]. Thus, the considered nonlinear system (1) can be described by the following form of the T-S model:

Remark 1:SinceE(h) is nonsingular, we can perform its inverse operation in the descriptor fuzzy system (2). In this case, the descriptor fuzzy system can be transformed into one that is nominal (nondescriptor). As pointed out in [27], when considering the T-S descriptor representation, the number of fuzzy inference rules will decrease so that the number of LMIs to controller design is remarkably reduced.

Here, without loss of generality, we only consider that the class of norm-bounded square integrable disturbance acts over the time interval [t1,t2], which is defined as below [28]:

This paper aims at to design a FSMC law, which can drive the system trajectories of the considered fuzzy descriptor model into the sliding surface function within a finite time,where the FTB subject to (c1,c2,[0,S],R,W[0,S],δ). Furthermore, sufficient conditions for designing the proposed FSMC law is derived in the form of LMIs.

III. DESIGN OF FSMC LAW BASED ON FTB

In this section, for the specified finite time and the initial state, we will perform the FTB of the FSMC descriptor system in both the reaching and sliding phases, and it will be shown that sufficient conditions for designing the proposed FSMC law is given in the form of LMIs.

A. Model Transformation

Firstly, motivated by [27] we can rewrite the T-S fuzzy descriptor model in (2) as below:

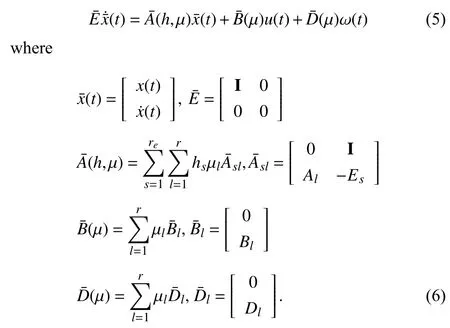
Remark 2:Note that, by using a descriptor redundancy approach, the fuzzy representation in the derivative matrix (2)is reformulated into the linear approach as shown in (5). In that case, it is easy to choose the Lyapunov matrix as below:

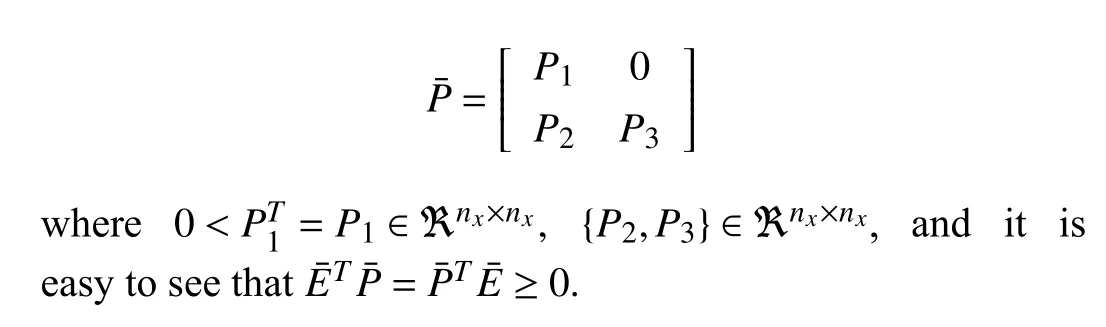
B. Design of FSMC Law

Firstly, based on the fuzzy descriptor system (5), an integral-type sliding surface function is constructed as below[15]:

with

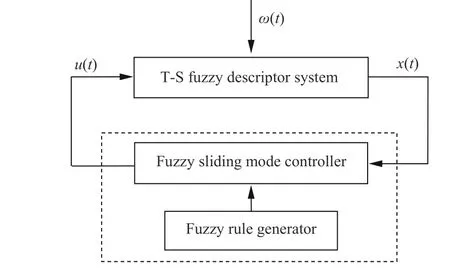
Fig. 1. Fuzzy sliding mode control of T-S fuzzy descriptor system.

C. Reaching Phase of FTB Within[0,S*]

Proof:Consider the Lyapunov function in the descriptorsystem domain,

D. Sliding Motion Phase of FTB Within[S*,S]

During the finite-time interval [S*,S] of the sliding phase,we will derive the sufficient conditions to ensure the FTB of the FSMC descriptor system. When the system trajectories arrive at the sliding surface, it has thats˙(t)=0. Thus, the equivalent controllerueq(t) is obtained as below:

Motivated by [35], [36], by augmenting the system (5) and the equivalent controller (37), it yields

Remark 4:Here, by further employing the descriptor redundancy representation we can avoid the inverse operation in the equivalent controller (37).

In the following, we will derive a sufficient condition to ensure the FTB of the FSMC descriptor system (38) within the finite-time interval [S*,S].

In addition, it can be seen from (44) that

E. Design of Controller Gain

Furthermore, the controller gain can be obtained as below:

F. Design Procedure for the FTB Algorithm

The detailed calculation steps of the proposed FTB algorithm for the FSMC descriptor system are summarized as follows:

1) Use the T-S fuzzy model method to describe the nonlinear descriptor system as shown in (1), and rewrite the T-S fuzzy descriptor model as shown in (5).

2) Choose a suitable matrix, so that(μ) is nonsingular,and solve Theorem 4 to obtain the controller gainKl. Given the initial statex(0), and the finite-timeS, and construct a FSMC lawu(t) as shown in (8) and (9);

IV. SIMULATION STUDY

The PV systems are built to transform sun irradiance into electrical power. However, building such systems come at a relatively high cost. All work done in the published literature focuses on increasing the efficiency of such systems and decreasing their cost. In order to show the effectiveness of the proposed control method, we consider a maximum power point tracking (MPPT) problem for a solar PV power system using a DC/DC boost converter as shown in Fig. 2, which consists of a solar PV array, an inductorL, a capacitorC0, and a load. Its dynamic model can be represented by the following differential equations [37]:

Fig. 2. A solar PV power with DC/DC boost converter.

In order to maximize the efficiency of PV power-generation systems, the electric characteristic of PV arrays is considered as follows [37]:

The normalized membership functions are given in Fig. 3,and we rewrite the T-S fuzzy descriptor model of the nonlinear PV system as below:

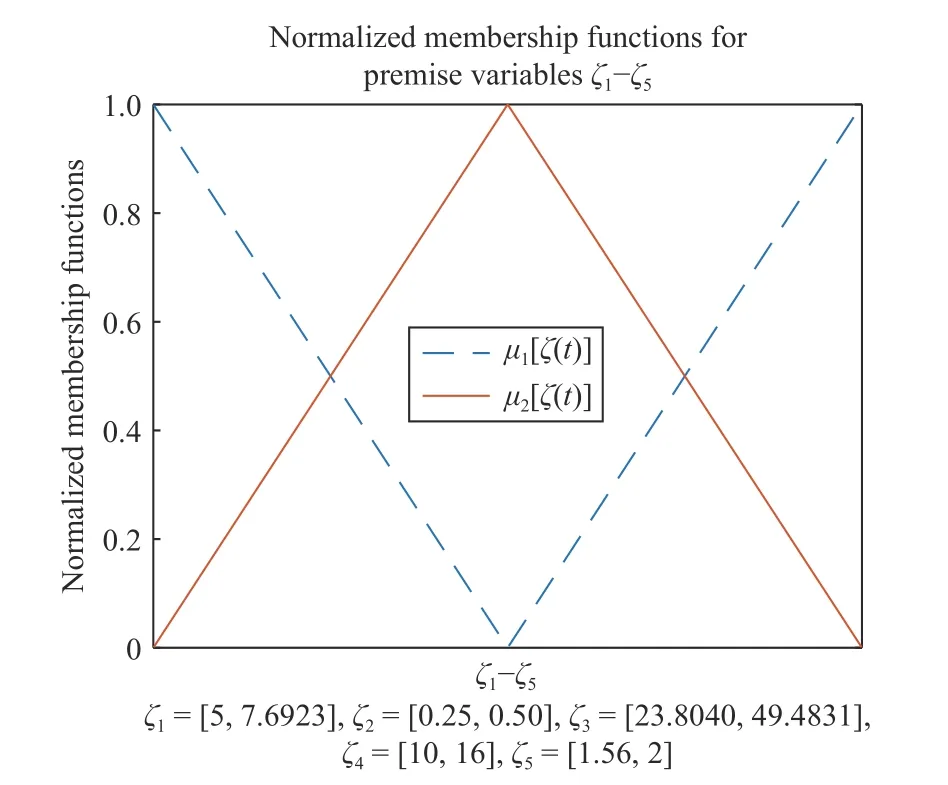
Fig. 3. Normalized membership functions.

With the above solution, the response of the sliding surface function is shown in Fig. 4. It is easy to see that the proposed FSMC can force PV system states around the sliding surface withinS=0.3 s, which is less than the pre-specified finite timeS= 1 s. The responses of PV system states by the proposed FSMC control strategy are shown in Fig. 5. It can be seen that the approximated MPPT of the PV nonlinear system can be achieved withinS=0.05 s. Moreover, we further compare with non-fuzzy sliding mode control, and the corresponding results are respectively given in Fig. 6. It is easy to see that the proposed fuzzy sliding mode control achieves better control performance in comparison with nonfuzzy sliding mode control. Note that the state trajectories of open-loop PV system are unbounded. However, the proposed FSMC control strategy ensures the state trajectories boundness, and the comparison ofxT(t)Rx(t) between the open-loop system and the closed-loop one is given in Fig. 7.Responses of the derivative of the statex(t) and control inputu(t)are respectively given in Figs 8 and 9.

Fig. 4. Response of the sliding surface function.

Fig. 5. State responses for the fuzzy SMC system.

Fig. 6. State responses for the linear SMC system.

xT(t)Rx(t)Fig. 7. Comparison of between open- and closed-loop control.

Fig. 8. Response of the derivative of the state x(t).

Fig. 9. Response of the control input u (t).

Remark 7:It is worth to point out that the proposed FSMC in (67) carries the advantages of both the fuzzy method and the sliding mode technique at the same time. The fuzzy method can be regarded as a powerful and flexible approximator, and the main feature of sliding mode approach is its fast response and robustness against uncertainties or disturbances. Figs. 5 and 6 have shown that the proposed FSMC achieves fast response against disturbances in comparison with non-fuzzy sliding mode control.

Remark 8:It is noted that all computations in the sequel were done in MATLAB R2018b running under Windows 10 PC. The computer used was equipped with Intel Xeon E-2276M 2.8 GHz CPU and 16 GB RAM. First, the desired SMC controller gains are solved off-line. The computational time using the FSMC design proposed in Theorem 4 is 218.5 s while the times using the linear SMC result are within 2.8 s.Then, after the off-line controller gains are obtained, for the considered fuzzy system, the SMC is implemented on-line.The computational time of the FSMC is 3.52×10-4s in each iteration while the computational time of the linear SMC is 3.05×10-4s. Moreover, the number of total decision variables using the FSMC design in Theorem 4 is 205 but the number of total decision variables on the linear SMC result is 116. Therefore, it is a trade-off between design complexity and desired control performance when considering with the applications of the FSMS and linear SMC.

Remark 9:Note that the choices of fuzzy premise variables and fuzzy rules have a great impact on control performance and computational complexities. Since the authors have tried different rules for this example, the selected premise variables are 5 and the selected fuzzy rules are 32, which have taken into account both the control performance and computational complexities. Thus, it will avoid the overfitting problem.

V. CONCLUSIONS

This paper proposes a novel fuzzy sliding mode control strategy to T-S fuzzy descriptor systems using a FTB method.By using a descriptor redundancy approach, the fuzzy representation in the derivative matrix is reformulated into a linear one. We introduce a fuzzy sliding mode control(FSMC) law, and it is shown that the proposed FSMC law ensures the FTB of the closed-loop fuzzy control systems over the reaching phase and sliding motion phase. Sufficient conditions for designing the proposed FSMC law is derived in terms of LMIs. The simulation study shows that the MPPT control of the PV nonlinear system can be achieved within a specified finite time..