Zoning Search With Adaptive Resource Allocating Method for Balanced and Imbalanced Multimodal Multi-Objective Optimization
2021-06-18QinqinFanandOkanErsoy
Qinqin Fan and Okan K. Ersoy,
Abstract—Maintaining population diversity is an important task in the multimodal multi-objective optimization. Although the zoning search (ZS) can improve the diversity in the decision space, assigning the same computational costs to each search subspace may be wasteful when computational resources are limited, especially on imbalanced problems. To alleviate the above-mentioned issue, a zoning search with adaptive resource allocating (ZS-ARA) method is proposed in the current study. In the proposed ZS-ARA, the entire search space is divided into many subspaces to preserve the diversity in the decision space and to reduce the problem complexity. Moreover, the computational resources can be automatically allocated among all the subspaces. The ZS-ARA is compared with seven algorithms on two different types of multimodal multi-objective problems(MMOPs), namely, balanced and imbalanced MMOPs. The results indicate that, similarly to the ZS, the ZS-ARA achieves high performance with the balanced MMOPs. Also, it can greatly assist a “regular” algorithm in improving its performance on the imbalanced MMOPs, and is capable of allocating the limited computational resources dynamically.
I. INTRODUCTION
MULTIMODAL multi-objective optimization problems(MMOPs) are commonly observed in the multiobjective optimization (MO) [1], [2]. Unlike general multiobjective optimization and multimodal optimization [3]-[9],the objectives of the multimodal multi-objective optimization(MMO) must not only achieve a good approximation in the objective space, but also locate enough equivalent Pareto optimal solutions in the decision space [10]. Therefore, maintaining the diversity in these two spaces is vital in the MMO [11],[12]. Until now, various multimodal multi-objective evolutionary algorithms (MMOEAs), which are called“regular” algorithms in this study, have been proposed and performed well on benchmark test suites. However, Liuet al.[13] have stated that existing “regular” MMOEAs may perform poor with the imbalanced MMOPs in which search complexities of Pareto optimal sets (PSs) are not the same in different regions. In other words, most proposed MMOEAs belong to convergence-first search methods, thus they may trap into easy regions and cannot find enough equivalent Pareto optimal solutions when these MMOPs are imbalanced.To alleviate the above-mentioned problem, Liuet al. [13]used a convergence-penalized density method to maintain the diversity in the decision space. Moreover, both exploitation and exploration strategies are used to improve the search efficiency. The results show that their proposed algorithm,called the “special” algorithm, performs better on these imbalanced MMOPs when compared with other “regular”algorithms.
Recently, Fan and Yan [11] proposed a zoning search (ZS)method considered as a decision space decomposition strategy to solve the balanced MMOPs. Intuitively, such a search strategy may also be employed to solve the imbalanced MMOPs since the ZS can reduce the search difficulty of problems in each subspace, i.e., the degree of imbalance in each subspace can be reduced, and help MMOEAs improve the diversity in the decision space. However, the same amount of computational resource is allocated in each search subregion in [11], which may reduce the search efficiency and waste computational resources, especially when the distribution ofPSs is unsymmetrical in the decision space.
To maintain the diversity in the decision space and take full use of limited computational resources, a zoning search with the adaptive resource allocating method (ZS-ARA) is proposed to solve the imbalanced and balanced MMOPs in the current study. In the ZS-ARA, the decision search space is divided into many subspaces for reducing the complexity ofPSs in each decision subspace, and computational resources can be automatically assigned among all the subspaces to improve their use efficiency. Results indicate that the ZSARA can perform well on both the balanced MMOPs and the imbalanced MMOPs. More importantly, the proposed algorithm can help a “regular” MMOEA (i.e., MO_Ring_PSO_SCD proposed by Yueet al. [14]) enhance its performance in solving the imbalanced MMOPs. Therefore, it can greatly reduce difficulties in the algorithm design.
Main contributions of the current work are described as follows:
1) Similarly to the ZS, the proposed ZS-ARA not only reduces search complexities of MMOPs in each subspace, but also reduces difficulties in designing improved algorithms,especially when MMOPs are imbalanced.
2) Unlike the ZS, the ZS-ARA is capable of assigning computational resources among all the subspaces. It is important for the balanced and imbalanced MMOPs to improve the use efficiency of computational resources.Namely, the proposed algorithm is able to automatically allocate more computational resources to promising regions.
The remaining sections of this paper are organized as follows: the MMO is introduced in Section II. Section III reviews the related works on MMO. Section IV presents the proposed algorithm. Experimental comparisons and analyses are reported in Section V. Section VI gives the conclusions and describes future works.
II. IMBALANCED MULTIMODAL MULTI-OBJECTIVE OPTIMIZATION
Compared with the imbalanced MMO, the balanced MMO has attracted more attention [13]. The former is introduced below.
Similarly to multi-objective optimization problems (MOPs),the imbalanced MMOPs can be formulated as follows:

A. Concepts of Multi-Objective Optimization
In this subsection, some terminologies and concepts of the MO are described as follows [15]-[17]:

B. Concepts of Imbalanced Multimodal Multi-Objective Optimization
For an MMOP, there are two main features [11]: i) like an MOP, more than one objective is conflicting; ii) at least one point in thePFhas different equivalent Pareto optimal solutions. Besides the above features, an imbalanced MMOP has additional one or two of the following features:
1) Search Stage:For a point in thePF, search complexities of at least two equivalent Pareto optimal solutions are different.
2) Selection Stage:For a point in thePF, selection pressures of at least two equivalent Pareto optimal solutions are different.
Compared with a general MO, preserving the population diversity may be more important in the MMO. This is because individuals in the population close to easy regions quickly when search complexities of points in the decision space are different.
C. Performance Metric
Achieving a goodPFapproximation (objective space) and locating sufficient equivalent Pareto optimal solutions(decision space) are equally important in the MMO. To demonstrate the effectiveness of the proposed algorithm, a Pareto sets proximity (PSP) [14], which is used to evaluate the similarity between the obtained solution set andPSs, is utilized on the balanced and imbalanced MMOPs. Moreover,an inverted generational distance-multi-modal (IGDM) [18],which can measure the quality of results both in the decision and objective spaces, is used to assess performances of MMOEAs on the imbalanced MMOPs.
ThePSPcan be defined as follows [14]:


III. RELATED WORK
Compared with the MO, the MMO has attracted fewer researchers, but it is commonly found in different fields. In recent years, some MMO test suites [14], [19]-[23] have been proposed to investigate performances of MMOEAs. Because the diversity in the decision and objective spaces is important in the MMO, advanced diversity maintaining/improvement strategies have been incorporated into MMOEAs to find more Pareto optimal subsets. For example, an Omni-optimizer proposed by Deb and Tiwari [19] used a crowding distance to maintain the diversity in the decision and objective spaces.Their proposed algorithm can locate multiple equivalent Pareto optimal solutions. Shiret al. [24] proposed a niching covariance matrix adaptation (niching-CMA) wherein a dynamic niching method is employed to maintain the diversity in the decision space and the objective space. The results indicate that the niching-CMA performs better than other algorithms used in the comparison. In [25], a multi-objective particle swarm optimizer with self-organizing mechanism(SMPSO-MM) is introduced to solve MMOPs. In the SMPSO-MM, the self-organizing map, the elite learning strategy, and the non-dominated-sort method with special crowding distance are employed to improve the population diversity and the search capability. The results indicate that the SMPSO-MM can find more equivalent Pareto optimal solutions and obtain a well-distributedPFwhen compared with other four MMOEAs. Yueet al. [14] used a ring topology and a special crowding distance to assist a multiobjective particle swarm optimization (called as MO_Ring_PSO_SCD) in improving the population diversity.Their results show that the MO_Ring_PSO_SCD performs well on 11 MMOPs. A decomposition-based evolutionary algorithm with addition and deletion operators (MOEA/DAD) [26] introduced by Tanabe and Ishibuchi is proposed to solve MMOPs. In the MOEA/D-AD, a set of reference individuals are utilized to preserve the diversity in the objective space, and a niching method is employed to maintain the diversity in the decision space. The achieved results show that the MOEA/D-AD can locate more equivalent Pareto optimal solutions on seven MMOPs when compared with other MMOEAs. To find enough equivalent Pareto optimal solutions and achieve a good distributedPF,Liuet al. [27] proposed a double-niched evolutionary algorithm (DNEA), in which a double sharing function is utilized to calculate the density of each solution in both decision and objective spaces. Their experiments show that diversity maintenance in both spaces is necessary for solving MMOPs. A differential evolution for multimodal multiobjective problems, called the DE-TriM, is introduced in [28].In this algorithm, a novel mating pool selection approach and a computational resource allocation strategy based on a set of reference points are employed to enhance its search capability on MMOPs. In [29], a multi-objective hill-valley evolutionary algorithm, termed the MO-HillVallEA, is proposed to solve MMOPs. In the MO-HillVallEA, the hill-valley clustering method is incorporated into the MAMaLGaM. The results indicate that the MO-HillVallEA is competitive. Note that most above-mentioned studies are based on niching methods.Although these niching methods, termed “soft isolation” in[11], can preserve diversity, their performances may be limited due to high environmental pressure and complex shape of Pareto optimal sets. Therefore, Fan and Yan [11] used a decision space composition strategy (called the ZS) to improve the diversity in the decision space and reduce the problem complexity. The experimental results show that the ZS is an effective approach to solve MMOPs. Additionally,Tanabe and Ishibuchi [30] reviewed existing related works on the MMO. However, almost all of the above mentioned studies belong to “regular” algorithms and are used to solve the balanced MMOPs. Unlike previous studies, Liuet al. [13]recently proposed a set of the imbalanced MMOPs. Moreover,a “special” algorithm, i.e., an evolutionary algorithm using a convergence-penalized density method (CPDEA), is introduced to solve them. The results show that the CPDEA can locate more equivalent Pareto optimal solutions in the decision space, but some “regular” MMOEAs are easy to trap into easy regions.
IV. ZONING SEARCH WITH ADAPTIVE RESOURCE ALLOCATING METHOD
A. Motivation
In [11], a decision space decomposition strategy, i.e., the ZS, is proposed to solve the balanced MMOPs. Moreover, the same computational resources are assigned to each search subspace. It may be helpful for some types of MMOPs whereinPSs are well distributed uniformly in the decision space. However, ifPSs in the decision space are not uniform or search complexities of the subspaces are different, using the same computational resources in each subspace will greatly waste limited computational resources. Therefore, assigning different computational resources in subspaces is an important task. To illustrate the above mentioned problems, two examples for the ZS-ARA without computational resource allocation (i.e., the ZS) are given as follows:
Case 1 (Each Subspace Has Equivalent Pareto Optimal Solutions):Resource allocation of the ZS is shown in Fig. 1.We can observe from Fig. 1 that the number of equivalent Pareto optimal solutions in each search subspace is different.If the ZS is used to solve Case 1, i.e., computational resources allocated in four subspaces are the same, then easy subspaces may not require so many computational resources. Therefore,allocating the computational resources among all the subspaces optimally is a promising approach to enhance the use efficiency of the computational resources.

Fig. 1. Resource allocation of the ZS (Case 1). The size of each circle denotes the used computational resource in each subspace. C1, C2, C3, and C4 (C1 = C2 = C3 = C4 in the ZS) denote the used computational resources in subspace-1, subspace-2, subspace-3, and subspace-4, respectively; C (C =C1 + C2 + C3 + C4) denotes the total computational resource.
Case 2 (Not All Subspaces Have Equivalent Pareto Optimal Solutions):Resource allocation of this case is illustrated in Fig. 2. It can be seen from Fig. 2 that there are no equivalent Pareto optimal solutions in two subspaces. If each subspace consumes the same computational resources, then limited computational resources will be wasted in unpromising subspaces. Therefore, how to effectively assign the computational resources is necessary.
Based on the above introductions, it can be concluded that allocating computational resources among all the subspaces is a promising method to improve the use efficiency of limited computational resources, especially with the imbalanced MMOPs. In other words, unlike the previously proposed zoning search [11] (i.e., each zoning is allocated the same computational resources), the ZS-ARA aims to allocate more computational resources to promising regions.
B. Proposed Method
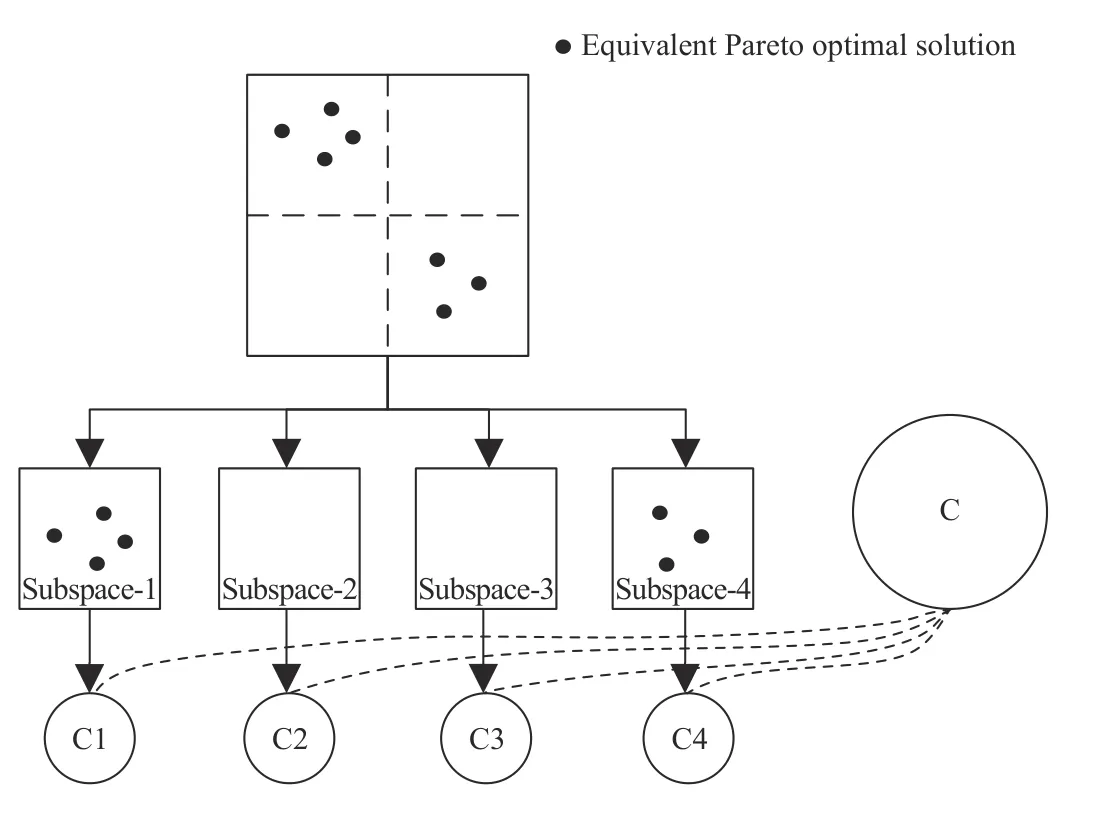
Fig. 2. Resource allocation of the ZS (Case 2). The size of each circle denotes the used computational resource in each subspace. C1, C2, C3, and C4 (C1 = C2 = C3 = C4 in the ZS) denote the used computational resources in subspace-1, subspace-2, subspace-3, and subspace-4, respectively; C (C =C1 + C2 + C3 + C4) denotes the total computational resource.
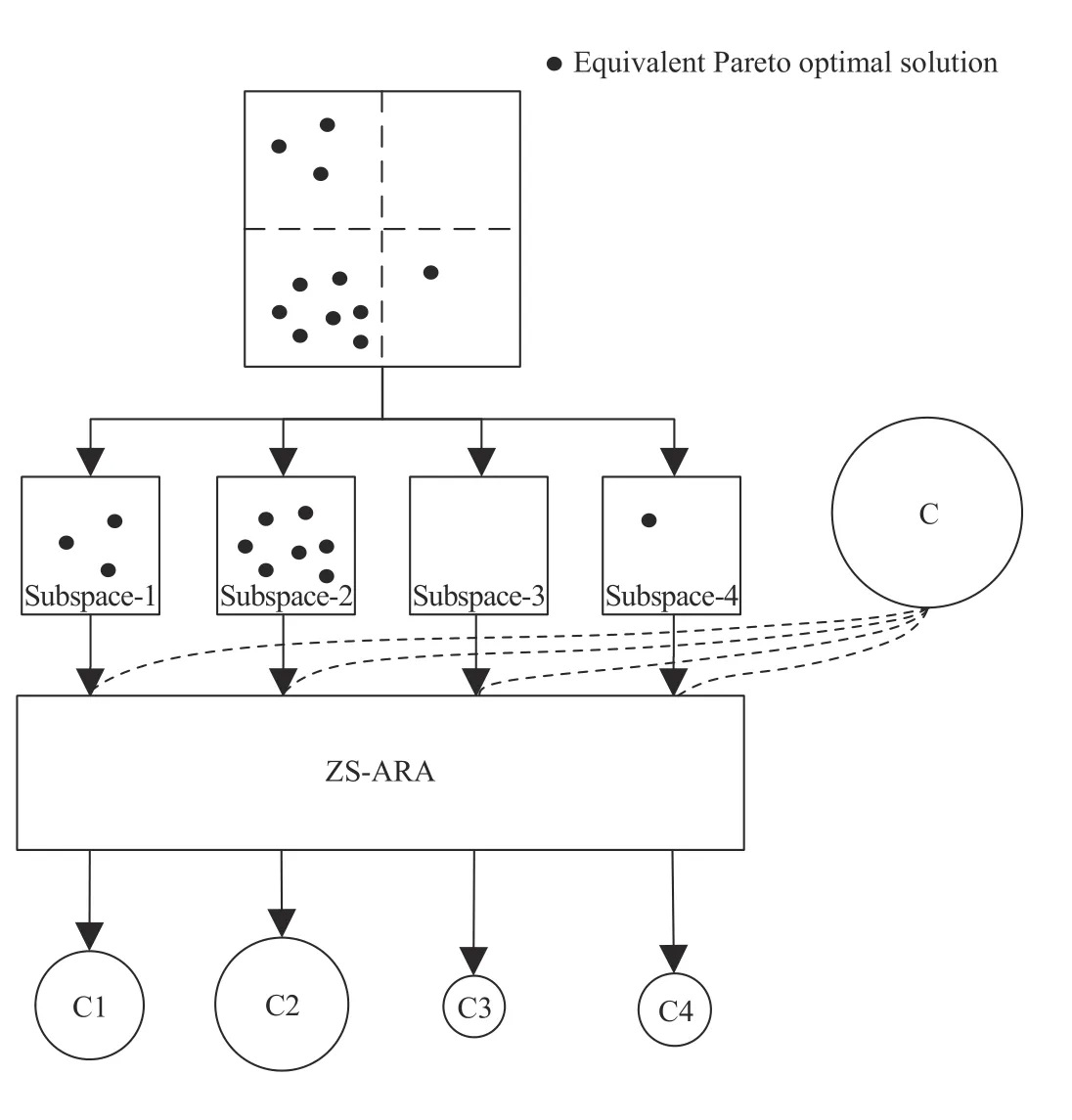
Fig. 3. Resource allocation of the ZS-SAR. The size of each circle denotes the used computational resources in each subspace. C1, C2, C3, and C4 denote the used computational resources in subspace-1, subspace-2, subspace-3, and subspace-4, respectively; C (C = C1 + C2 + C3 + C4) denotes the total computational resource.
To alleviate the above-mentioned issue, the ZS-ARA is introduced to improve the use efficiency of limited computational resources. Unlike the ZS, the computational resources can be automatically assigned to different subspaces in the current study. To illustrate the ZS-ARA visually, its resource allocation process is shown in Fig. 3. It can be observed from Fig. 3 that the distributions of equivalent Pareto optimal solutions in all subspaces are different. For example, no equivalent Pareto optimal solutions are in the subspace-3, thus it is allocated less computational resources.However, the subspace-2 gives more computational resources to locate equivalent solutions. Namely, unlike the ZS, C2 is not equal to C3 in the proposed algorithm. Therefore, the use efficiency of the computational resources can be improved via the ZS-ARA, especially when the computational resources are limited.
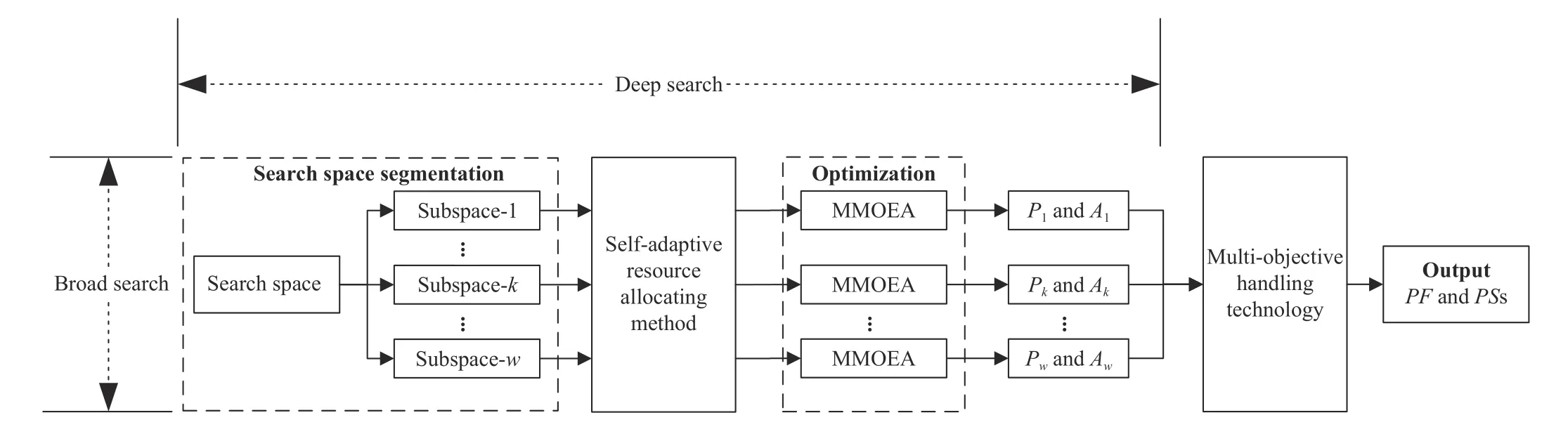
Fig. 4. Generic framework of ZS-ARA.
The ZS-ARA can both maintain the population diversity and reduce the search difficulty in each subspace like the ZS,and make full use of the given computational resources.Additionally, the search space segmentation and the resource allocation are achieved in the ZS-ARA.
1) Search Space Segmentation:Similarly to the previous study [11],h(1 ≤h≤D) (the number of selected variables)variables are chosen randomly and are divided intoq(q> 1)equal segments. The number of subspaces is equal tow=qh.
2) Computational Resource Allocation:To implement automatic allocation of the computational resources, the quality of non-dominated individuals in each subspace is used to guide the selection probability updating of the selected MMOEA in the current study.
The steps can be described as follows:
Step 1:Obtain approximatePF, denoted as (Pi,i∈{1,2,...,w}), and its corresponding solutionsAi(in the decision space) in thei-th subspace.
Step 2:Achieve thePFapproximation and theAin the entire space. Namely,P=Selection(P1∪P2···∪Pw) and its corresponding solution setAin the decision space. The number of objective vectors in thePis denoted asN.
Step 3:Compute the number of objective points ofi-th subspace (denotedNi) in theP.
Step 4:Update the selection probability of the selected MMOEA in thei-th subspace, denotedSPi. It can be calculated as follows:
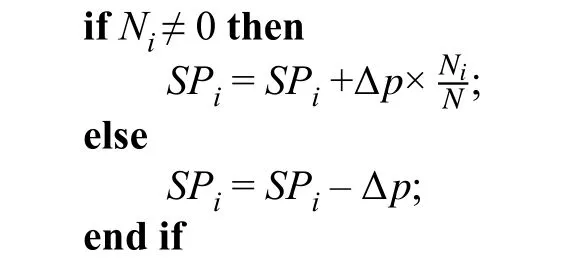
where Δpis a constant selection probability in each update.From Step 4, it can be observed that the computational resource can be automatically allocated among all the subspaces. In other words, if an MMOEA can find more nondominated individuals in the corresponding subspace, then it will be given more computational resources. Additionally, ifSPi> 1 orSPi< 0,SPi= 1 orSPi= 0.05, respectively.
C. Overall Implementation of ZS-ARA
Based on introductions in Sections IV-B-1) and IV-B-2), the overall implementation of the ZS-ARA is presented in Algorithm 1. The first step is dividing the entire search space into many subspaces (line 1). Subsequently, an MMOEA is used to find approximatePFandPSin each subspace based on its selection probability (lines 3-7). The selection probability of the selected MMOEA in each decision subspace is updated (lines 8-10) when the learning period (LP) is equal to a fixed number of generations. A largeLPvalue means that the selection probability updating of an MMOEA in each subspace is slower, i.e., the learning time is longer. Finally,PFapproximation andPSs are obtained in the entire search space.
Apart from the pseudocode of the ZS-ARA shown in Algorithm 1, its generic framework is also illustrated in Fig. 4.It can be seen from Fig. 4 that other existing search space segmentation methods, self-adaptive resource allocation approaches, MMOEAs, and multi-objective handling methods can be utilized in the ZS-ARA. Moreover, its performance is affected by the above four parts. Additionally, assuming that the computational time complexity of the ZS-ARA, which includes the search space segmentation, the resource allocating method, and the optimization and selection operators, isO*. Clearly, theO*is mainly determined by the computational time complexity ofk-th MMOEA.

Algorithm 1 ZS-ARA Input: S: entire search space;LP: learning period;w: number of subspaces;G: number of generations;SPi: the selection probability of MMOEA in the i-th subspace, .1: Search space segmentation (see Section IV-B-1)).2: while the stopping criterion is not satisfied do 3: for each subspace Si in {S1, S2,…, Sw}do 4: if SPi > rand then 5: Use an MMOEA to find approximate PFi and PSi;6: end if 7: end for 8: if LP∣G then 9: Update SPi (see Section IV-B-2));10: end if 11: end while S election(P1 ∪P2···∪Pw) S election(A1 ∪A2···∪Aw)i ∈{1,2,...,w}Output: P = and PSs =.
From the perspective of sampling, the broad search means algorithms are capable of sampling uniformly in the entire search space, and the deep search represents the capability of algorithms to sample densely within a given search space.Therefore, the broad search can be implemented by segmenting the decision space and the deep search can be carried out via reduced subspaces in the ZS-ARA, i.e., the proposed algorithm can also balance the broad search and the deep search.
V. EXPERIMENTAL RESULTS AND ANALYSES
To assess the performance of the ZS-ARA, two different types of test suites, which include the balanced [14], [31] and imbalanced [13] MMOPs, are used in the current study. The ZS-ARA is compared with five other algorithms on balanced MMOPs and five other algorithms on imbalanced MMOPs.The competitors include ZS [11], MO_Ring_PSO_SCD [14],Omni-optimizer [32], DN-NSGAII [33], NSGAII [34],TriMOEA-TA&R [18], and CPDEA [13]. Except for the CPDEA, other algorithms can be considered as “regular”MMOEAS. Furthermore, the Pareto sets proximity (PSP)[14], which can measure the similarity is used to evaluate performances of all the compared algorithms on the balanced and imbalanced MMOPs, andIGDM[18] is employed to assess performances of all the compared algorithms on the imbalanced MMOPs.
To analyze the achieved results, two non-parametric statistical tests, i.e., Wilcoxon’s rank sum test [35] and Friedman’s test [36], with a 0.05 significance level are used.Marks “+”, “-”, and “≈” denote that the ZS-ARA performs remarkably better, worse, and approximately the same as its competitor. Except for results with the imbalanced MMOPs,all results are obtained with MATLAB (R2016a) on a desktop computer with Windows 7 operating system (64 bit).
A. Experimental Settings
For the balanced MMOPs, population sizes of all the compared algorithms are set to 800 and the maximum number of function evaluations is set to 160 000. For the imbalanced MMOPs, population sizes of the proposed algorithm are set to 20 on two-objective problems and 60 on three-objective problems, respectively. Population sizes with other compared algorithms are the same as in [13], i.e., the population sizes of compared algorithms are set to 60 and 120 on two- and threeobjective imbalanced MMOPs, respectively. The maximum numbers of function evaluations are set to 18 000 on twoobjective problems and 36 000 on three-objective problems,respectively. Additionally, each compared algorithm is executed for 40 independent times on the balanced and the imbalanced test suites. Besides the above parameter settings,other parameters of all compared algorithms are set as suggested in their original studies. Note that four-objective problems in the imbalanced MMOPs are not used in the current study. The main reason is that the MO_Ring_PSO_SCD considered as a “regular” algorithm performs poorly on imbalanced multimodal many-objective problems. Finally,bothhandqare set to 2, i.e., the number of subspaces is 4 on all MMOPs.
B. ZS-ARA With Balanced MMOPs
To demonstrate the performance of the ZS-ARA, 22 balanced MMOPs are used in this experiment. Moreover, it is compared with four other algorithms and the ZS. The mean and standard deviation values ofPSPare reported in Table I.Moreover, the best results are shown in bold and the Wilcoxon’s rank sum test is used to analyze the results obtained by all compared algorithms in a statistical way.Similarly to the ZS, Table I indicates that the performance of the proposed algorithm is significantly better than those of four MMOEAs. Therefore, it can be concluded that the ZSARA is able to assist other MMOEAs in locating more equivalent solutions. It is also interesting to observe from Table I that the overall performance of the ZS-ARAMO_Ring_PSO_SCD is slightly better than that of the ZSMO_Ring_PSO_SCD. This is because the search difficulty of the equivalent optimal subset is almost the same in each subspace, i.e., the performance difference between the ZSMO_Ring_PSO_SCD and the ZS-ARA-MO_Ring_PSO_SCD is small on the balanced MMOPs. However, except for the functions MMF2, MMF11, and MMF12, the ZSMO_Ring_PSO_SCD cannot outperform the ZS-ARAMO_Ring_PSO_SCD on any balanced MMOPs in terms of the mean values. Clearly, allocating computational resources in the ZS can further improve the search efficiency of MMOEAs.
Overall, similarly to the ZS, the ZS-ARA is also an effective approach to assist MMOEAs in improving their performances on the balanced MMOPs.
C. ZS-ARA With Imbalanced MMOPs
To further testify the performance of the ZS-ARA, four two-objective and four three-objective imbalanced MMOPs are utilized in this experiment. Note that four four-objective MMOPs have not been selected in this subsection. This is because the ZS can only assist MMOEAs in finding more equivalent Pareto optimal solutions in the decision space, and the MO_Ring_PSO_SCD cannot perform well on manyobjective optimization problems.
Table II reports the meanIGDMvalues and the statistical analysis results obtained by the Wilcoxon’s rank sum test, and the best result is shown in bold. As observed in Table II,compared with four “regular” MMOEAs, i.e., MO_Ring_PSO_SCD, TriMOEA-TA&R, DN-NSGAII, and DNEA, the ZSARA can assist the “regular” MMOEA, i.e., MO_Ring_PSO_SCD, in finding more equivalent optimal solutions with all the imbalanced MMOPs. The main reason is that the ZS-ARA both improves the broad search capability and preserves the population diversity to avoid premature convergence, and reduces the unbalancedness of the imbalanced MMOPs in each subspace. Table II also shows that the performance of the ZS-ARA -MO_Ring_PSO_SCD is better than that of the ZSARA-MO_Ring_PSO_SCD since the former can automatically assign the computational resource to reduce waste of resources in useless search regions. It should be noted that the CPDEA considered as a “special” MMOEA is also used to solve the imbalanced MMOPs, but the proposed ZS-ARA-MO_Ring_PSO_SCD produces better results on all the functions in a statistical way, except for two functions IDMPM2-T1 and IDMP-M3-T4. It can be concluded that the ZSARA can greatly improve the performance of the “regular”algorithm in solving the imbalanced MMOPs. In other words,the proposed algorithm may be a promising approach to help“regular” and “special” MMOEAs locate more equivalent optimal solutions, especially in the decision space. For the IDMP-M2-T1 and the IDMP-M3-T4, Table II indicates that,although the ZS-ARA can reduce the complexity of problems and enhance the allocation capability of computational resources, it is inevitable that some computational resources will be wasted during the entire selection process. Therefore,both the ZS-ARA and the selected MMOEA are equally important in solving the imbalanced MMOPs.
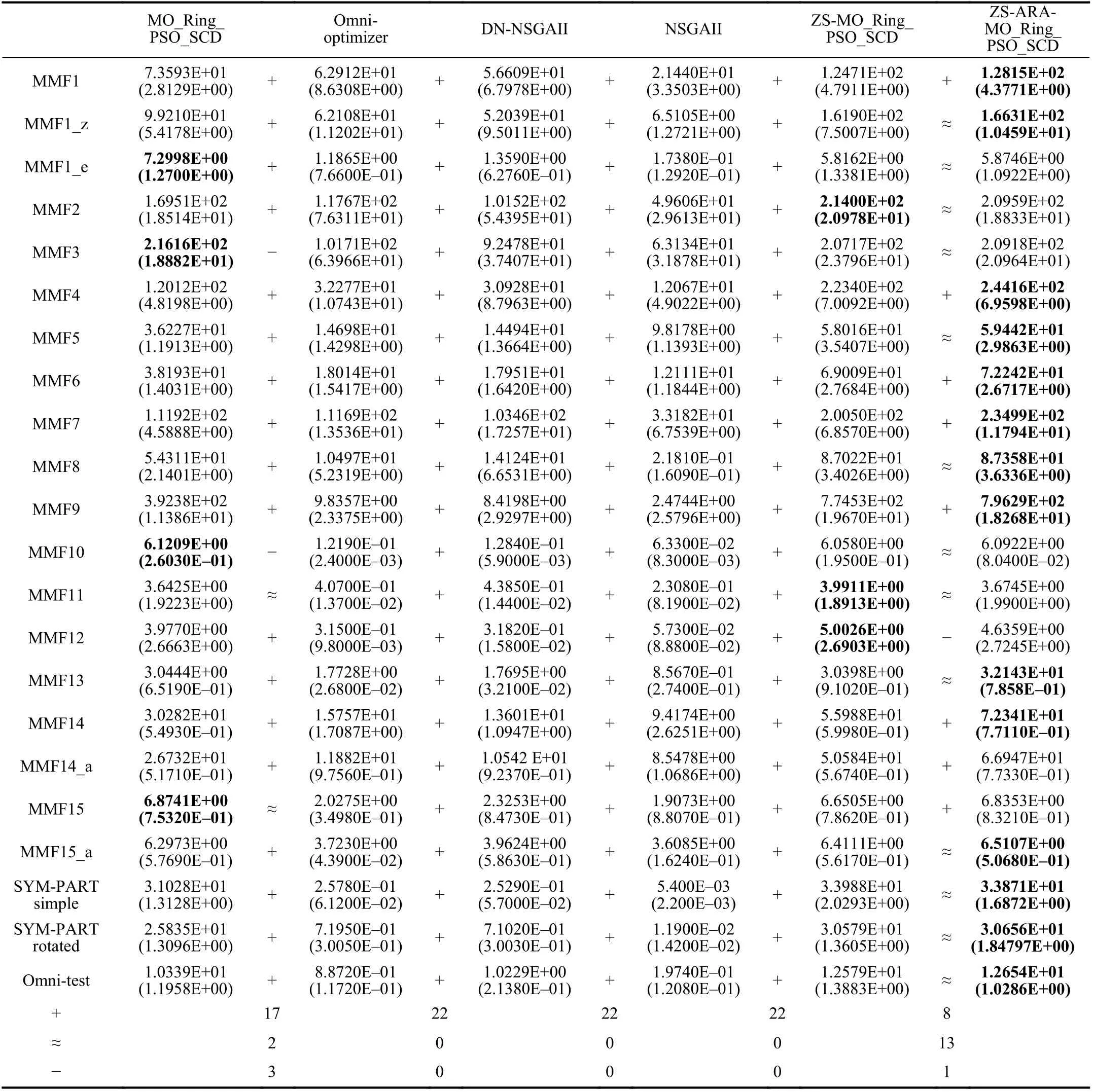
TABLE I MEAN AND STANDARD DEVIATION VALUES OF ALL COMPARED ALGORITHMS WITH RESPECT TO PSP
Besides the achievedIGDMvalues, thePSPis utilized to evaluate all compared algorithms in the decision space and the results (including the mean values and statistical analysis results) are given in Table III. It can be observed from Table III that the ZS-ARA-MO_Ring_PSO_SCD outperforms the TriMOEA-TA&R, the DN-NSGAII, and the ZS-MO_Ring_PSO_SCD on all imbalanced MMOPs in a statistical method.Moreover, the proposed algorithm performs better than the CPDEA on all imbalanced MMOPs except for the IDMP-M2-T1 and the IDMP-M3-T4. For the IDMP-M2-T1, the reasons may be twofold: 1) The CPDEA is a “special” algorithm to solve imbalanced MMOPs, while the MO_Ring_PSO_SCD selected in the proposed algorithm is a “regular” algorithm.Therefore, it may be reasonable that the performance of the ZS-ARA-MO_Ring_PSO_SCD is worse than that of the CPDEA. However, Table III shows that the proposed method can significantly improve the performance of the MO_Ring_PSO_SCD on this problem. 2) The computational resource allocation method may not be optimal since it must balance the greedy selection and the random selection on different types of imbalanced MMOPs. This is analyzed in Section V-D-1). For the IDMP-M3-T4, it is a difficult imbalanced MMOP to be solved, thus “special” algorithms can locate more equivalent solutions. Compared with the MO_Ring_PSO_SCD, the proposed algorithm performs better on all imbalanced MMOPs except for the IDMP-M3-T4. It means that the ZS-ARA is capable of assisting the MO_Ring_PSO_SCD in locating more equivalent solutions.For the IDMP-M3-T4, Table III indicates that the MO_Ring_PSO_SCD outperforms the ZS-ARA-MO_Ring_PSO_SCD. This is because the IDMP-M3-T4 has many local optimal regions. Moreover, the existence of the standard deviation value of the proposed algorithm on the IDMP-M3-T4 means that the performance of the proposed algorithm is not robust when problems are difficult to solve.

TABLE II MEAN VALUES OF ALL COMPARED ALGORITHMS WITH RESPECT TO IGDM
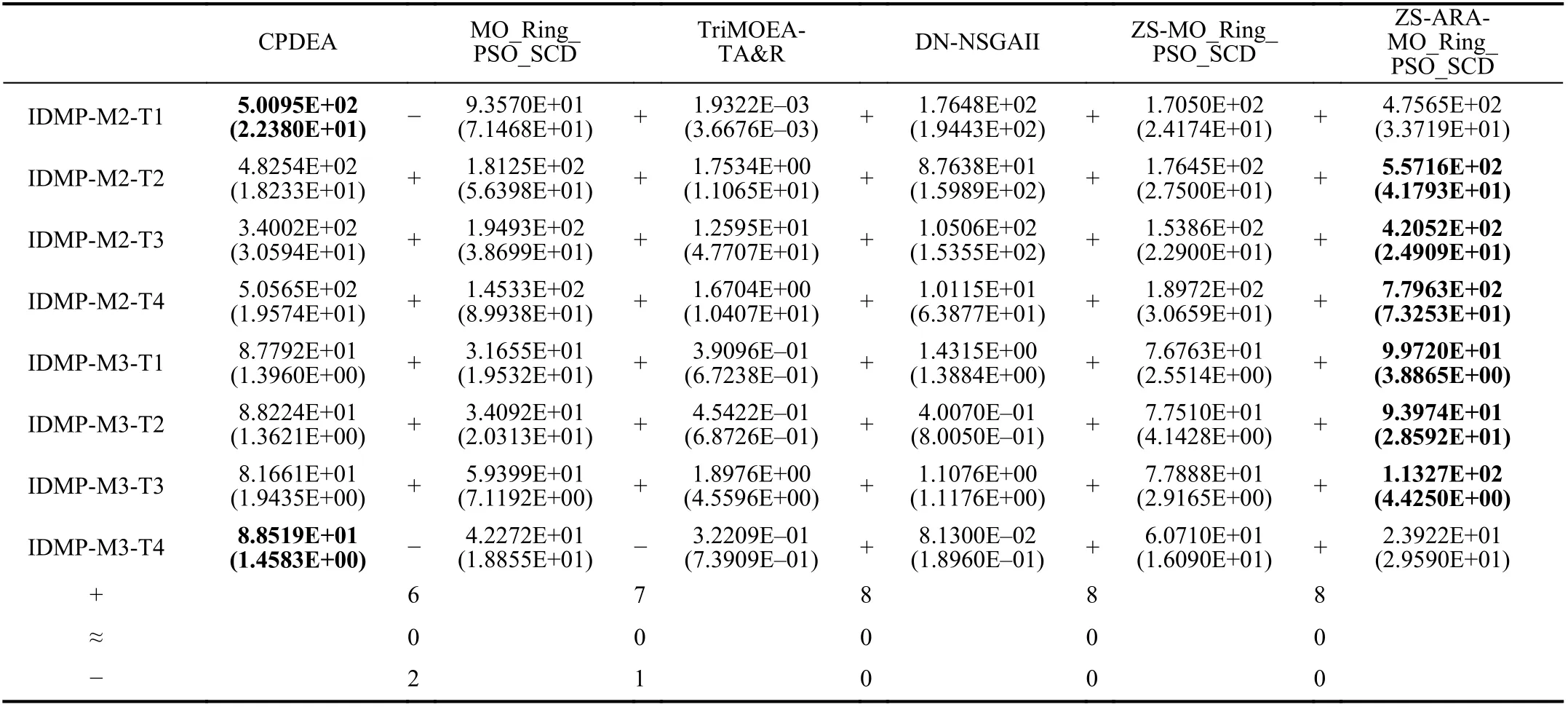
TABLE III MEAN VALUES OF ALL COMPARED ALGORITHMS WITH RESPECT TO PSP
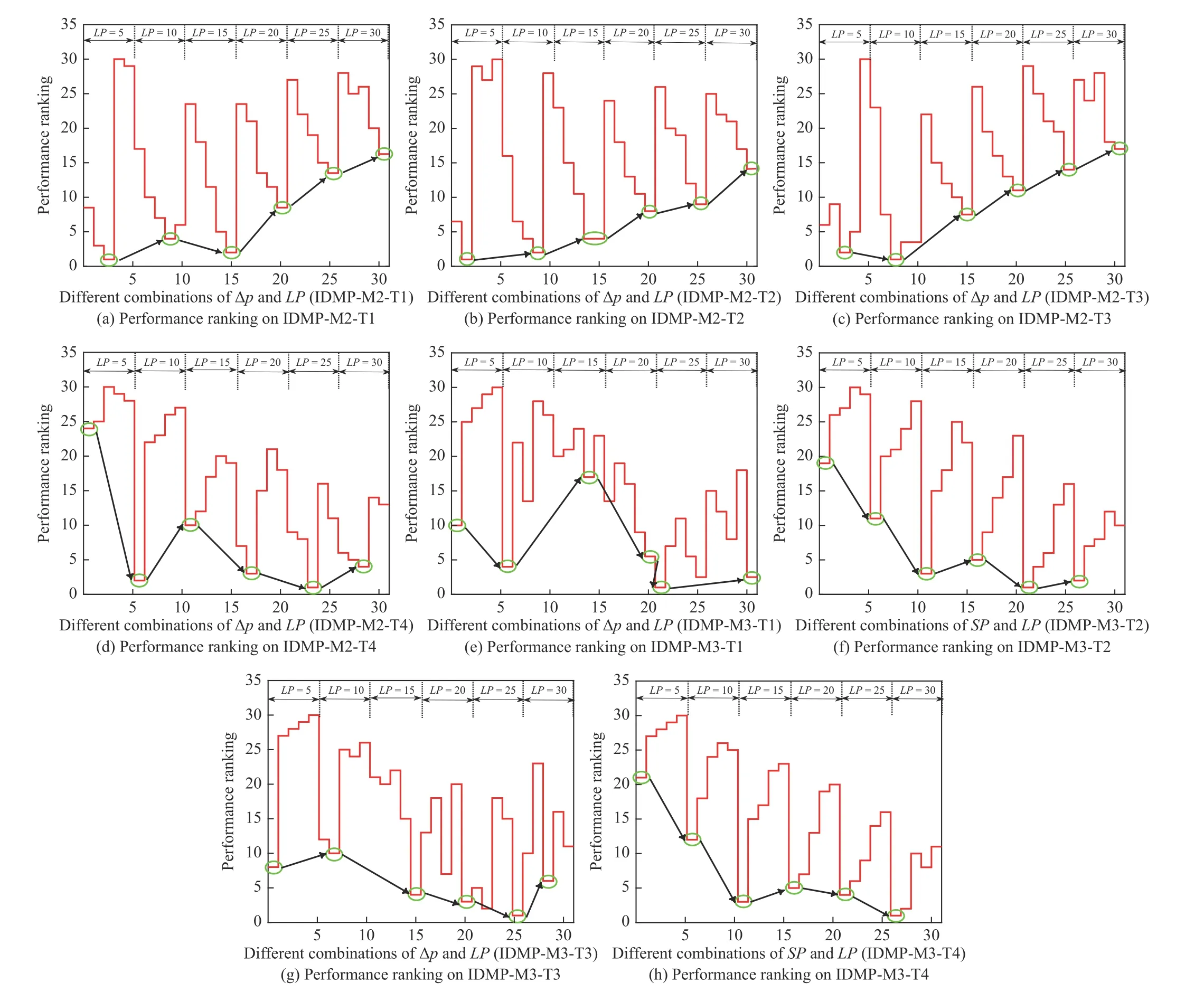
Fig. 5. Performance rankings of different combinations of SP and LP on eight imbalanced MMOPs (Ellipse denotes the best performance ranking for each LP value).
Based on the above analyses, it can be concluded that the ZS-ARA can help other “regular” MMOEAs find more equivalent solutions on imbalanced MMOPs. Moreover, how to allocate computational resources or improve learning efficiency is still an important and difficult task.
D. Parameter Sensitive Analysis
1) Impacts ofΔp and LP:Generally, a greedy or random resource allocating strategy may not always be effective to solve different types of problems. In the ZS-ARA, the learning period (LP) and the selection probability ( Δp) greatly influence its allocation efficiency of the computational resource. Namely, a large value ofLPwill provide a longer time for the ZS-ARA to distinguish which subspaces should be given more computational resources. In contrast, a smaller value of Δpwill give more time for the ZS-ARA to avoid false selection. Eight imbalanced MMOPs are utilized to investigate these two parameters in the ZS-ARA. For each function, the experiments are independently run 20 times. Moreover, values of ΔpandLPare selected from the sets {0.1, 0.2, 0.3, 0.4, 0.5}and {5, 10, 15, 20, 25, 30}, respectively. Therefore, the number of combinations of ΔpandLPis 30.
The performance rankings obtained by the Friedman’s test are plotted in Fig.5. The combinations of (5, 0.1), (5, 0.2), (5,0.3), …, (30, 0.5) are numbered as 1, 2, 3, …, 30 in Fig. 5.From Figs. 5(a)-5(c), it can be seen that a smaller value ofLPcan assist the ZS-ARA in producing better results. Similarly toLP, a larger value of Δpis capable of improving the performance of the ZS-ARA. Therefore, we can conclude that the greedy resource assigning strategy should be adopted to solve simple imbalanced MMOPs. In Figs. 5(d), 5(f), and 5(h), it can be observed that a larger value ofLPand a smaller value of Δpcan help the ZS-ARA to locate more equivalent Pareto optimal solutions and obtain a well-distributedPF. In other words, giving more learning time for the ZS-ARA is necessary when optimization problems are complex.Additionally, Figs. 5(e) and 5(g) show that a large value ofLPcan improve the search capability of the ZS-ARA, but the value of Δpis hard to determine for differentLPvalues.
Based on the above observations, it can be concluded that there are no fixedLPand Δpvalues for the proposed algorithm to maintain its optimal performance on all types of the imbalanced MMOPs. To further investigate theLP, the overall performance rankings of allLPvalues are illustrated in Fig. 6. Clearly,LP= 25 performs the best among allLPvalues. Therefore,LP= 25 is chosen with the ZS-ARA.Moreover, a dynamic adjustment strategy is used to balance the greedy and the random selection, i.e., Δp= 0.1 +0.4G/Gmax(Gdenotes the current generation andGmaxdenotes the maximal number of generations) is chosen in the current study.
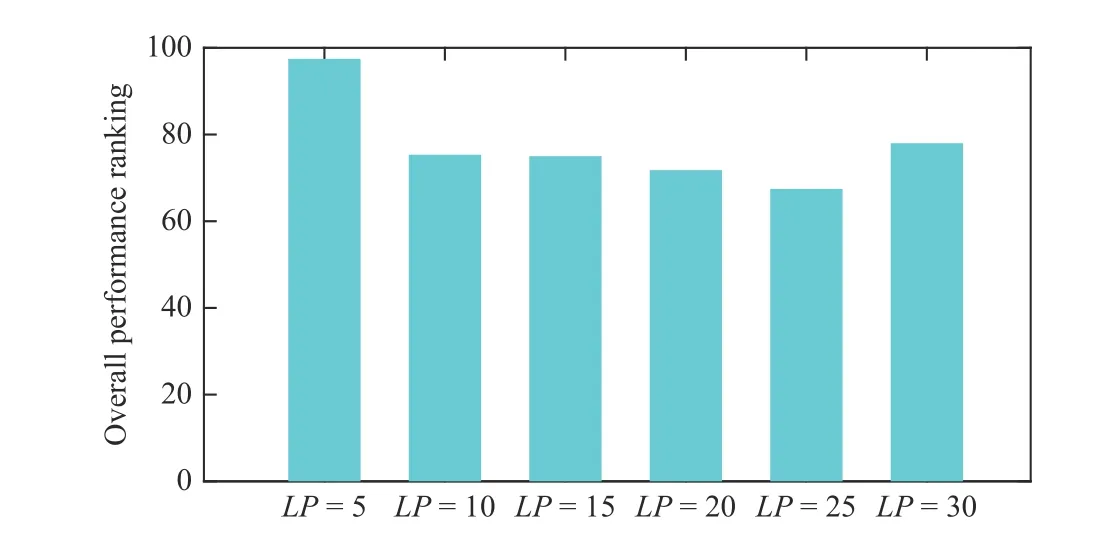
Fig. 6. Overall performance rankings of different LP values.
2) Impact of Population Size:In addition to the two parameters investigated in Section V-D-1), the population size in the ZS-ARA is also investigated with eight imbalanced MMOPs in this subsection. Because two different population sizes are used on two-objective and tri-objective imbalanced MMOPs [13], the population sizes are chosen from the set{20, 40, 60, 80, 100, 120} on two-objective problems and the set {60, 80, 100, 120, 140, 160} on tri-objective problems.The influences of different population sizes on the ZS-ARA are illustrated in Fig. 7. Fig. 7(a) shows that the performance of the proposed algorithm decreases with the increased population size. Namely, a small population size can help the ZS-ARA find more equivalent optimal solutions and achieve a well-distributedPF. This is because a smaller population size can provide more generations to assist the selected MMOEA in finding equivalentPSs. It can be also seen from Fig. 7(b)that using a small population size in each subspace improves the performance of the ZS-ARA on functions IDMP-M3-T1,IDMP-M3-T2, and IDMP-M3-T3.NP= 80 produces the best result on the function IDMP-M3-T4. Therefore, too small population size in each subspace may negatively influence the performance of the ZS-ARA when solving complex optimization problems. Overall, a small population size used in each subspace can produce better results when compared with a large population size, but the setting of population size in the ZS-ARA should be based on the problem complexity of each application.
Based on the above analysis, the population size is set to 20 on two-objective imbalanced MMOPs and 60 on tri-objective imbalanced MMOPs.
E. More Computational Resources on Imbalanced MMOPs
As stated in [37], [38], it is possible that an algorithm cannot find a good solution, even if more computational resources are provided. Therefore, the effectiveness of the ZSARA is further investigated with eight imbalanced MMOPs in this subsection. Moreover, two compared algorithms MO_Ring_PSO_SCD and CPDEA are used in the experiment.
The maximum number of function evaluations, which is double in Section V-C, is set to 36 000 on two-objective imbalanced MMOPs and 72 000 on tri-objective imbalanced MMOPs. The compared algorithms are named as MO_Ring_PSO_SCDX2, CPDEAX2, and ZS-ARA-MO_Ring_PSO_SCDX2. Their population sizes are the same as in Section VC.
The mean and standard deviation values ofIGDMare presented in Table IV. Note that the results of the MO_Ring_PSO_SCD, the CPDEA, and the ZS-ARAMO_Ring_PSO_SCD are directly taken from Table II. It can be observed from Table IV that the performances of three algorithms can be improved when more computational resources are given. Additionally, the MO_Ring_PSO_SCDX2l and CPDEAX2 can achieve better results on all problems, but the ZS-ARA can assist the MO_Ring_PSO_SCD in producing much better results, especially on four difficult three-objective imbalanced MMOPs. Therefore, it can be concluded that if more computational resources are given, the ZS-ARA is a more effective and promising approach to solve imbalanced MMOPs.
F. Obtained PSs and Resource Allocation Rates in Each Subspace
The study in [13] reported that the “regular” MMOEA, i.e.,MO_Ring_PSO_SCD, could not find allPSs on the imbalanced MMOPs since the MO_Ring_PSO_SCD lacked good diversity maintaining capability, whereas their proposed algorithm is capable of locating allPSregions in the decision space. To visually testify the effectiveness of the ZS-ARA,eight imbalanced MMOPs are used in this experiment. The obtainedPSs of the proposed algorithm in a single run are plotted in Figs. 8 and 9. From Figs. 8(a)-8(d), we observe that the ZS-ARA assists the “regular” algorithm in finding two well-distributed equivalent optimal subsets. For four triobjective problems, Figs. 9(a)-9(d) exhibit that the ZS-ARA is capable of helping the MO_Ring_PSO_SCD locate allPSs.The proposed algorithm can also find more equivalent optimal solutions in easy regions, such as subspaces 1 and 3. Note that the difficulties in finding equivalent optimal solutions are increasing in subspaces 1, 3, 4, and 2. The main reason is that the MO_Ring_PSO_SCD does not belong to “special” algorithms, which can locate enough equivalent optimal solutions in difficult regions. Moreover, because each subspace has an equivalent Pareto optimal subset, the computational resource is evenly allocated. Namely, the computational resource may not be enough to find more equivalent Pareto optimal solutions in difficult regions. Overall, the ZS-ARA is a promising approach to help MMOEAs find more equivalent optimal subsets.

Fig. 7. Influence of different population sizes.

TABLE IV MEAN VALUES OF ALL COMPARED ALGORITHMS WITH RESPECT TO IGDM
Besides the obtainedPSs, the resource allocation rate in each subspace is also illustrated in Figs. 8 and 9. We observe from Figs. 8(a)-8(d) that the ZS-ARA can assign more computational resources in promising regions. Therefore, the proposed algorithm can allocate the computational resource more effectively when compared with the ZS. Of course, it is inevitable that some computational resources would be wasted to determine which regions contain equivalent Pareto optimal solutions. Additionally, Figs. 9(a)-9(d) shows that each subspace almost uses the same computational resource since each of them has equivalent optimal solutions. Therefore, the ZS-ARA is capable of automatically allocating the computational resources based on the obtainedPSs of each subspace.
VI. CONCLUSIONS AND FUTURE STUDY
A zoning search with adaptive resource allocation (ZSARA) is proposed in the present work. In the ZS-ARA, the entire decision space is divided into many search subspaces to reduce the problem complexity and the computational resources are automatically allocated in each subspace to effectively use the limited computational resources. The ZSARA is compared with a “special” algorithm and eight“regular” algorithms on the balanced and imbalanced MMOPs. The experimental results show that the proposed algorithm is capable of maintaining its performance on the balanced MMOPs as the ZS and assists a “regular” algorithm in improving its performance on the imbalanced MMOPs. It should be noted that the proposed ZS-ARA-MO_Ring_PSO_SCD can perform better than a “special” MMOEA (i.e.,CPEEA) on most imbalanced MMOPs.
The sensitivities of Δp,LP, and population size are analyzed in Section V-D. The results indicate that the performance of the ZS-ARA is influenced by these parameter settings. The ZS-ARA is compared with the MO_Ring_PSO_SCD in Section V-E when more computational resources are provided. The experimental results show that giving more computational costs does not mean that the MMOEA can find more equivalent Pareto optimal solutions in the decision space on the imbalanced MMOPs. However, the ZS-ARA can help“regular” MMOEAs enhance their performances. The obtainedPSs and resource allocation rates are investigated in Section V-F. The results show that the ZS-ARA can help the MO_Ring_PSO_SCD locate all thePSregions and allocate more computational resources in promising regions.
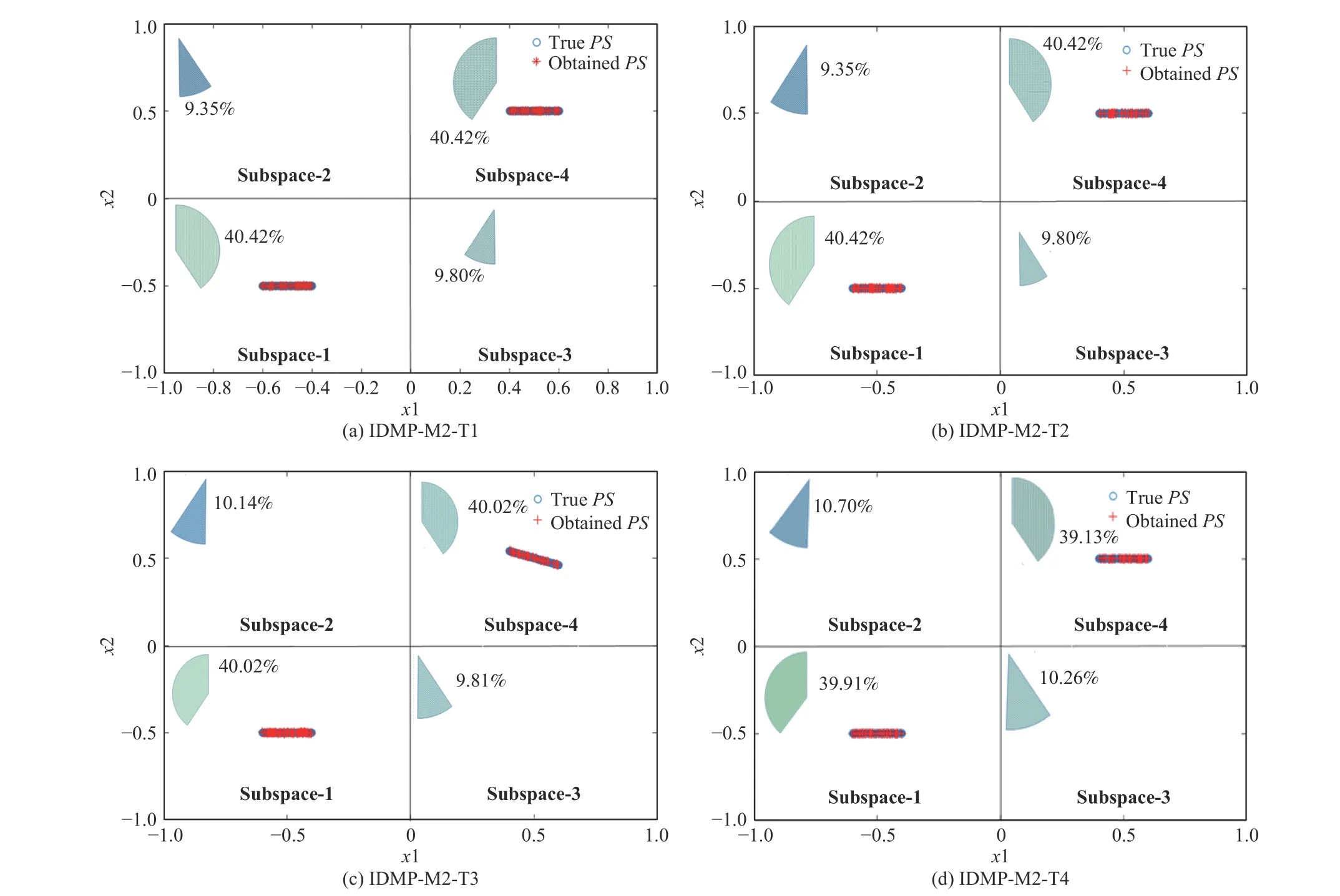
Fig. 8. Obtained PSs and resource allocation rate in each space on four 2-D imbalanced MMOPs in a single run.

Fig. 9. Obtained PSs and resource allocation rate in each space on four 3-D imbalanced MMOPs in a single run.
Although the ZS-ARA is an effective approach to solve low-dimensional balanced and imbalanced MMOPs, it still has the following problems: 1) How to generate subspaces is a challenging task when the search space is high-dimensional;2) How to effectively allocate the computational resources when the number of subspaces is much greater than four.Moreover, improving the allocation efficiency of computational resources is still an important task; 3) The results show that the performance of the ZS-ARA is greatly influenced by selected MMOEAs, thus it is important to further design more advanced MMOEAs. In our future work,principal decision variables will be specially selected.Moreover, balancing short-term and long-term learning methods will be studied to improve the resource allocation efficiency. Finally, high-performance computing methods such as parallel computing and cloud computing will be used with the ZS-ARA to save the computational time.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Speed and Accuracy Tradeoff for LiDAR Data Based Road Boundary Detection
- Distributed Asymptotic Consensus in Directed Networks of Nonaffine Systems With Nonvanishing Disturbance
- Finite-Time Fuzzy Sliding Mode Control for Nonlinear Descriptor Systems
- A Novel Rolling Bearing Vibration Impulsive Signals Detection Approach Based on Dictionary Learning
- Dual-Objective Mixed Integer Linear Program and Memetic Algorithm for an Industrial Group Scheduling Problem
- Output-Feedback Based Simplified Optimized Backstepping Control for Strict-Feedback Systems with Input and State Constraints
