煤炭自动定量装车控制策略设计

2021-06-16齐世炜付主木陶发展司鹏举

河南科技大学学报(自然科学版) 2021年5期

齐世炜，孙畅，付主木, b，李玲，陶发展, b，司鹏举, b

(河南科技大学 a.信息工程学院；b.河南省机器人与智能系统重点实验室；c.国际教育学院，河南洛阳 471023)

0 引言

煤炭是中国的基础能源和重要原料，在国民经济中占有重要的战略地位[1]。在煤炭装车环节方面，传统人工装车模式由于中间人工环节繁杂，经常出现车辆滞留、通行缓慢等现象[2]。因此，为了提高装车精度与效率，亟需开发煤炭快速定量装车自动控制系统。

近几年，中国对自动装车系统的研究逐渐兴起[3]。文献[4]借鉴高速公路电子不停车收费(electronic toll collection, ETC)系统，设计了面向矿山的全自动车辆识别系统、自动称质量系统和自动连续装车系统，但缺乏较为先进的控制算法。文献[5]提出了基于内模原理的比例-积分-微分(proportional integral differential, PID)控制算法，依靠可编程逻辑控制器(programmable logic controller, PLC)控制技术实现给煤设备控制、牵引列车速度控制与装车计量检测，但当模型不匹配时容易出现问题。文献[6]设计了全自动火车煤矿装车系统，重点研究了自动装车的伺服控制系统，提高了装车精度，但伺服系统中的调节器采用传统的PID调节器，无法实现PID参数的自适应整定[7-9]。文献[10]针对定量装车提出了混合控制技术，采用定量粗装、衡量和精确添加的分层控制策略，极大地提高了装车精度，但在实际应用中较为复杂。综上所述，目前的煤炭自动定量装车控制系统要么缺乏较为先进的控制策略，要么控制策略相对简单难以应对复杂多变的客观情况或控制策略在实际应用中较为复杂。因此，本文提出了一种基于模糊推理的PID参数自适应整定控制系统。针对控制系统建立数学模型，实现系统的模糊PID控制方法并设计模糊控制器。对控制系统中存在影响系统性能的环节提出补偿策略，并进行仿真验证及试验测试。

1 控制系统组成与特性

1.1 控制系统组成

本煤炭自动定量装车控制系统由给煤仓给料系统、计量带式称质量给煤系统、液压闸门控制系统、电气控制系统、传感器检测系统等子系统组成。控制系统核心部分为给煤仓给料系统，给煤环节决定装车系统的装载精度。实现快速精准装车，关键部分也在给煤环节。本文所设计的给煤仓给料系统示意图如图1所示，给料口由液压闸门的开闭控制给料的启停，液压闸门的开启状态决定瞬时给煤量的多少。当煤炭从给料口放出，落至计量带式称质量给煤机上进行称质量，煤炭经过称质量给煤机运送至缓冲仓，落入装载车厢，完成动态称质量装车。

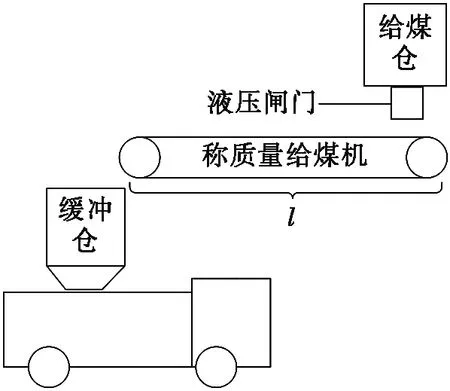
图1 给煤仓给料系统示意图

1.2 控制系统特性

控制系统核心被控对象为放料闸门，在放料闸门给煤过程中可近似视为自平衡单容过程。此过程可用一阶惯性环节[11]描述为：

(1)

其中：K为过程的放大系数；T为过程的时间常数；s为时域函数拉普拉斯变换下的复参数。

在皮带传输煤炭装车过程中，煤炭要经过长度为l的带式称质量给煤机，经时间τ后才进入车厢，此过程为纯滞后过程，可用一阶时滞环节[11]描述为：

G2(s)=e-τs,

(2)

其中：τ为过程的纯滞后时间。

因此，整个给煤装车环节可描述为：

(3)

对于本文控制系统，K=3，T=1.1，τ=0.3。

2 模糊PID控制

2.1 模糊PID控制实现原理

煤炭自动定量装车要求在尽可能短的时间内完成精准给料，实现这一过程的关键环节在于对给煤仓闸门的有效控制[12]。以闸门的开度为控制依据，设装车过程中给煤仓的瞬时给煤量(闸门开度)为P(t)，传感器检测到的煤堆实时高度为h(t)，期望高度为H，H与h(t)之差记为δ(t)。

经多次测试可以得出接近真实值的装煤密度ρ，装车前激光雷达检测出车厢的长和宽分别为l和w，假设目标装车质量为M，则装车的期望高度为：

(4)

由于一维模糊控制器只通过偏差值变化进行控制，很难反映实际使用过程中输出变量的动态特性，在控制精度上难以达到满意的效果。二维模糊控制器，输入为偏差和偏差的变化率，因为其具有偏差的变化量，能够更好地展现被控对象的动态特性，效果上优于一维模糊控制器[13]，故选用二维模糊控制器。基于以上分析可设计出如图2所示的模糊PID控制系统，利用模糊推理，对控制系统的PID参数KP、KI、KD进行实时整定(整定值为ΔKP、ΔKI、ΔKD)。

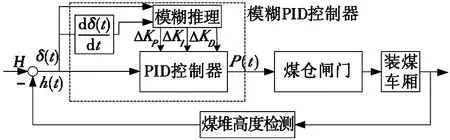
图2 模糊PID控制系统原理图

装煤过程中，各时刻下料速度及下料量不同，则所需最优PID参数也不同。以期望高度与检测煤位高度的偏差δ(t)、偏差的变化率δ(t)/d(t)作为二维模糊控制器输入，闸门开度为输出，在运行中不断判断δ(t)和δ(t)/d(t)的变化情况，运用模糊推理对3个参数进行自适应整定。

2.2 史密斯补偿

由于控制系统中存在滞后环节，仅靠PID控制很难获得良好的控制质量。时滞环节具有响应滞后的特点，这将导致系统需经过较长的调节时间并产生明显的超调[14]。

由控制系统闭环传递函数可知：特征方程中含有时滞环节e-0.3s，这是导致常规PID控制下系统出现较大超调、振荡的原因。史密斯补偿算法可以实现对于纯滞后对象的补偿[15]，其基本思路为:在控制系统中增加环节或增加控制支路，使系统的控制通道以及系统传递函数的分母不含有纯滞后环节[16]，从而改善控制系统的控制性能及稳定性。史密斯补偿基本原理如图3所示。图3中：Gp(s)为增加补偿环节后的等效补偿函数；Gc(s)为PID调节器;g(s)为传递函数不含时滞的部分[17]。

图3 史密斯补偿原理示意图

由图3可得等效补偿函数为：

(5)

此时，系统闭环传递函数为：

(6)

将式(5)代入式(6)可得：

(7)

此传递函数特征方程不再含有时滞环节，从而将消除时滞环节对系统的影响。

2.3 模糊PID控制器设计

2.3.1 隶属度函数选取

将模拟量系统误差δ(t)、误差变化率δ(t)/d(t)、系统控制变量u(t)离散化得到数字量，分别记为E(n)、D(n)和U(n)。将E(n)和D(n)作为二维模糊控制器的输入[18]：

E(n)=S(n)-y(n),D(n)=E(n)-E(n-1)，

(8)

其中：S(n)为系统的理想输出；y(n)为实际输出。

模糊规则[19]为：

如果E(n)为正且D(n)为正，则ΔU(n)为正；如果E(n)为正且D(n)为负，则ΔU(n)为0；

如果E(n)为负且D(n)为正，则ΔU(n)为0；如果E(n)为负且D(n)为负，则ΔU(n)为负，

其中，ΔU(n)为控制器输出的变化量。

对输入输出变量E(n)、D(n)和U(n)均采用对称、均匀全交叠的三角形隶属度函数[20]，为便于分析，把所有变量的论域设计为基本论域[-1,1]，并将此类模糊控制器称为通用模糊控制器。在进入通用模糊控制器之前，将输入信号E(n)、D(n)通过正规化因子GEi、GDi进行正规化变换转换到基本论域上，模糊控制器输出信号U(n)在输入被控过程之前也必须通过正规化因子GU进行反正规化转换到实际论域，即：

E*=GEiE(n),D*=GDiD(n),U(n)=GUU*，

(9)

其中：i=1，2且E*，D*，U*∈[-1,1]。

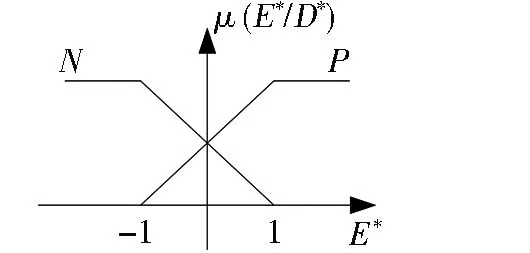
图4 输入变量的三角形隶属度函数

加权平均法解模糊公式为：

(10)

根据前文所述模糊规则，在任意时刻每条激活的规则为：

经模糊推理及解模糊可以得到：

经反正规化变换，可得：

则全局模糊PID控制器输出为：

数字PID控制算法公式为：

(11)

对比各项系数可得模糊整定参数为：

则修正后的PID参数为：

KP=KP0+ΔKP,KI=KI0+ΔKI,KD=KD0+ΔKD。

2.3.2 模糊规则表制定

针对不同情况下的料高，将料高偏差E、料高偏差变化率D的论域划分为[0, 6]，对不同的料高偏差E及偏差变化率D采用ZO(零)、SS(小小)、SB(小大)、MS(中小)、M(中)、BS(大小)、BB(大大)描述，其含义为检测料高与期望料高偏差E从小到大，对应料高偏差D的变化率由慢到快。即论域等级E=D=[0, 1, 2, 3, 4, 5, 6]，对应的模糊子集E=D=[ZO, SS, SB, MS, M, BS, BB]。

根据工程实践经验及PLC参数整定设置试验，KP的最佳取值范围为[0.2, 1.6]，KI的最佳取值范围为[0.1, 1.0]，KD的最佳取值范围为[0.02, 0.1]。取PID参数的初值KP0=0.08，KI0=0.03，KD0=0.01。将ΔKP、ΔKI、ΔKD的论域同样划分为[0, 6]，即ΔKP=ΔKI=ΔKD=[0, 1, 2, 3, 4, 5, 6]，对应的模糊子集ΔKP=ΔKI=ΔKD=[ZO, SS, SB, MS, M, BS, BB]，量化因子取K(ΔKP)=0.2，K(ΔKI)=0.1，K(ΔKD)=0.005。

模糊化处理后，制定模糊规则进行模糊推理。通常考虑以下情况：

(Ⅰ)当偏差E较大时，系统处于响应阶段，此时误差变化率D变化较快，为了使动态响应快，KP应较大；但为了避免积分饱和，出现较大的超调量，应限制积分强度，可令KI=0；同时，为防止微分饱和，KD不宜太大。

(Ⅱ)当偏差E大小处于中间位置，系统处于上升阶段，误差变化率D变化适中，此时KP、KI、KD应取值适中，尽量防止超调，同时还需兼顾系统的动态响应。

(Ⅲ)当偏差E较小时，系统处于微调阶段，误差变化率D变化较快，为得到较好的稳态性能，应适量增大KP、KI；同时为了防止振荡，在偏差E未进入较小可接受范围前，应适当加大KD，以使系统快速稳定，之后，可适量减小KD，以保证系统的稳定性。

根据以上分析，针对不同情况的料高偏差E(n)、偏差变化率D(n)，可分别建立KP、KI、KD的模糊控制规则，见表1。

表1 KP、KI、KD模糊规则

3 仿真分析与试验测试

在MATLAB/SIMULINK软件中建立系统仿真模型，对系统动态特性及稳态特性进行仿真分析。选用模糊PID控制算法模拟装车过程，并选择常规PID控制算法作为对比，通过仿真对比分析控制系统在简单闭环比例控制、常规PID控制、模糊PID控制下对阶跃信号的跟踪情况，进一步在试验平台进行测试。

3.1 系统性能仿真分析

3.1.1 无史密斯补偿下系统性能仿真分析

在闭环比例控制、常规PID控制、模糊PID控制下，通过仿真测试控制系统对阶跃响应的跟踪状况进行系统性能分析。向控制系统输入阶跃信号，系统在闭环比例控制、常规PID、模糊PID控制算法下的阶跃响应如图5所示。仿真过程中模糊控制器在不同时刻整定出的ΔKP值如图6所示。

图5 无史密斯补偿下不同控制算法阶跃响应

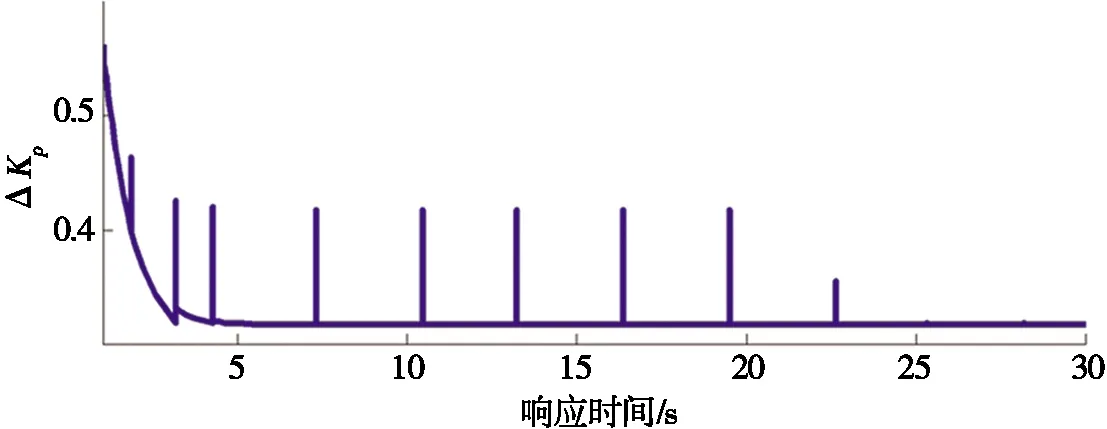
图6 无史密斯补偿下模糊整定ΔKP值

由图5可以看出：闭环比例控制在响应前期存在较大跳变且存在较大稳态误差；常规PID控制下，系统响应前期存在较大(约40%)的超调并且调节时间较长(约10 s)；而模糊PID调节时间较短(约5 s)且无超调量。但由图6可以看出：模糊控制器整定出的ΔKP值存在频繁跳变。

3.1.2 史密斯补偿下系统性能仿真分析

加入史密斯补偿环节后，闭环比例控制、常规PID控制、模糊PID控制下的阶跃响应如图7所示。仿真过程中模糊控制器在不同时刻整定出的ΔKP值如图8所示。

图7 史密斯补偿下不同控制算法阶跃响应

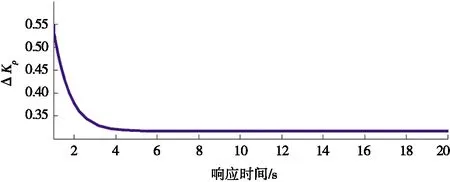
图8 史密斯补偿下模糊整定ΔKP值

由图7可以看出：加入史密斯补偿环节后，闭环比例控制在响应前期不再出现剧烈跳变，但依旧存在着较大的稳态误差。常规PID控制下，系统超调量明显减小(约为20%)，系统调节时间也减少了6 s左右；而模糊PID控制下，不存在超调，调节时间也更短(4 s左右)，系统性能得到改善。由图8可以看出：加入史密斯补偿环节后，模糊整定出的ΔKP不再出现跳变。

3.2 控制系统模拟装载仿真分析

由3.1.2节分析可知：闭环比例控制下，系统存在较大跟踪误差，模糊PID控制较常规PID控制具有更好的响应特性，采用模糊PID控制算法模拟装载过程并用常规PID控制作为对比。假设某次装车目标装载量为500 kg，常规PID和模糊PID控制下的装车模拟质量变化曲线如图9所示。

由图9可以看出：模糊PID控制算法下，1.8 s即达到目标装载质量的80%，而常规PID控制下，2.1 s左右才达到该装载质量；并且常规PID控制下起始阶段存在明显的迟滞，而模糊PID控制算法下，整个装载过程都更为流畅，反应更迅速灵敏。模糊PID控制算法较常规PID更稳定，响应速度更快。

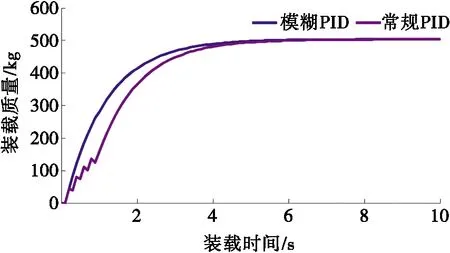
图9 装车模拟仿真质量变化曲线

3.3 试验平台测试

在试验平台进行装车测试，目标装载质量为500 kg，多次测试取平均值。装车试验测试质量变化曲线如图10所示。由图10可知：常规PID控制算法下，4 s以前系统响应较迟滞，10 s达到目标装载质量；模糊PID控制下，系统响应较迅速，8.5 s达到目标装载质量。模糊PID控制较常规PID控制的装载时间缩短了15%。常规PID控制的平均装载质量为498.6 kg，模糊PID控制的平均装载质量为499.2 kg。常规PID控制的装车误差为0.28%，模糊PID控制的装车误差为0.16%，装车误差降低了42.86%。模糊PID控制较常规PID控制反应速度更快，装载误差更小，模糊PID更能满足行业对装载快速性及准确性的要求。