基于小波降噪-曲线相似程度的锂离子电池内短路故障诊断方法
2021-06-15韩孝耀
甘 伟,韩孝耀
(华南理工大学机械与汽车工程学院,广东 广州 510641)
锂离子电池因其具有能量密度高、循环寿命长等优点,在新能源汽车领域得到广泛的应用[1-2],但当追求更高的能量密度时,安全隐患也随之而来[3]。其中,内短路是锂离子电池常见的故障类型,是引发热失控的主要诱因,因此内短路的提前预警是提高电池运行安全性的重要途径之一[4]。Seo等[5]提出一种基于卷积神经网络的锂离子电池内短路故障诊断方法,为提高预测精度,该方法通过放大相对于高强度恒流放电信号较弱的自放电信号来提高预测精度,随后使用带有32个卷积层及8个池化层的卷积神经网络完成内短路故障诊断。Hong等[6]提出一种基于改进多尺度熵的锂离子电池故障诊断方法,通过将不同起点的粗粒度序列求得的样本熵平均后得到改进多尺度熵值,从而成功提取电池故障早期信号的多尺度特征,实验结果表明该方法能够有效监测电池组单体电池连接故障及热失控故障。然而,上述方法都有一定的缺陷,例如所提取特征在故障早期不明显,使用的方法如神经网络需要大量的样本且预测精度高度依赖样本质量,多尺度熵方法计算时间过长难以实现实时在线诊断等。针对上述问题,本文提出基于小波降噪-曲线相似程度的锂离子电池内短路故障诊断方法,建立基于交叉验证的多分辨率小波降噪方法[7],使用动态时间规整方法计算降噪后曲线的相似程度作为报警阈值,最后通过模拟内短路实验所得数据验证方法的可行性与有效性。
1 多分辨率小波降噪
多分辨率小波分析是一种通过不同函数子空间内的尺度函数实现函数多分辨率表示的方法,能够将一个给定函数分解为一个低频信号和不同分辨率下的高频信号,因具有正交性、对称性、短支撑性、多尺度等特征,被广泛用于信号的分解、重构与降噪。
锂离子电池的充电电压信号可表示为:
V(t)=f(t)+ε(t)
(1)
式中:V(t)为采集到的电池充电电压;f(t)为理想电压,即无噪声的电压信号;ε(t)为信号噪声;t为时间。
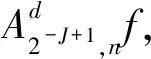
(2)

对于降噪信号A20V(t),降噪的目标是使电压降噪信号A20V(t)与理想电压信号f(t)平方误差最小,即:
(3)
式中:RSE为目标函数;N为信号长度。
本文采用交叉验证[8]的方法估计RSE,如图1所示,其中M=⎣N/2」,⎣」为下取整。

图1 交叉验证过程
将实验获取的电压信号按照时刻t的奇偶性划分,对奇数点信号进行两点光滑得到均匀估计值fe*,表示为:
(4)
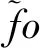
(5)
式中:ISE为近似目标函数。
本文通过最小化RSE确定降噪参数如小波类型、阈值处理的方式、分解的层数等,达到最大化小波降噪效果,从而提高方法预测精度。
以多种句式混合,造成参差错落的节奏变化,既体现了朱熹碑志铭文的特点,也体现了朱熹对不同诗歌体式的理解与掌握。《知南康军石君墓志铭》的铭文可为例证:
2 动态时间规整
动态时间规整,又称为DTW,是一种用以度量长度不同的两个时间序列相似程度的算法[9]。对于待测量时间序列Q={q(1),q(2),…,q(n)}及模板时间序列C={c(1),c(2),…,c(m)},使用满足一定条件的时间规整函数W(n)描述待测时间序列与模板时间序列的时间对应关系,将所求两个时间序列匹配时的累积最小距离作为曲线相似程度。具体计算步骤如下:
1)为了对齐两个序列,构造一个n×m的矩阵网络,矩阵(i,j)处的元素表示q(i)和c(j)的欧氏距离,即:
d(i,j)=[q(i)-c(j)]2
(6)
式中:d(i,j)为距离。
2)定义规整路径W,W的第k个元素为wk=(i,j)k。规整路径表示一条从点(1,1)到点(i,j)通过网格矩阵中若干点的路径,通过的网格点即两个时间序列对应的时间点,即:
W=w1,w2,…,wKmax(m,n)≤K≤m+n-1
(7)
式中:wK为路径上经过的第K个点。
同时,规定如果路径通过网格点(i,j),那么下一个通过的网格点必为以下3种情况之一:(i+1,j)、(i,j+1)及(i+1,j+1)。

(8)
通过式(8)可求得γ(m,n),所求最短距离γ(m,n)越小,序列Q={q(1),q(2),…,q(n)}与C={c(1),c(2),…,c(m)}的相似程度越高,反之相似程度则越低。
3 模拟内短路实验
锂离子电池内短路故障的发生会在某一瞬间产生大量的热,进而导致热失控,造成财产损失和人员伤亡。为了有效评估锂离子电池内短路性能,世界各国的组织和机构制定了一系列模拟内短路实验方法[10]。
本文采用并联等效电阻模拟内短路的实验方法,该方法可重复性好、实现简单,能够通过并联阻值的大小模拟内短路的程度,缺点是不能够模拟对锂离子电池造成真实的损伤。本文从数据驱动的角度出发,使用不同程度内短路电池充电循环的数据完成对锂离子电池内短路的故障诊断,上述缺点不会对整个方法的有效性和可用性产生影响,故采用并联等效电阻模拟内短路。实验时,将锂离子电池与不同阻值的等效电阻并联,模拟不同程度的内短路,同时通过开关控制内短路的发生。
本次实验使用了11个不同阻值的电阻模拟不同程度内短路,并联的电阻阻值越小,自放电越严重,内短路程度越深。本文使用锂离子电池满充时的自放电电流大小来衡量模拟内短路的程度,表1为并联电阻的阻值及对应自放电电流大小。
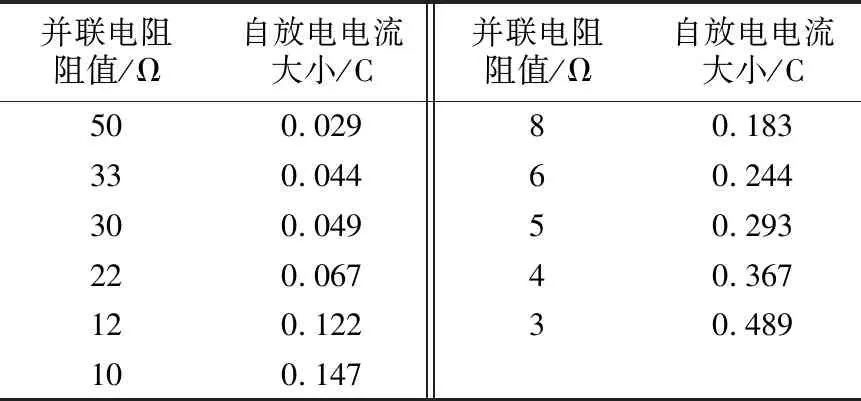
表1 并联电阻阻值及自放电电流大小
一般情况,当锂离子电池自放电电流大小达到0.5 C,即认为该电池的内短路程度已十分严重,接近热失控的发生,故实验取并联电阻阻值为3 Ω时所求最短规整路径距离故障特征为报警阈值。
4 实验结果与分析
实验所用锂离子电池为某公司型号为BLP621的电池,实验温度为室温(25±5) ℃,以0.5 C电流恒流充至4.4 V,静置1 h后,以1.0 C电流恒流放至2.8 V,随后静置1 h。在开始充电的瞬间打开开关,开始模拟内短路,记录充电过程中的电压变化。共计进行16次充放电循环,其中前5次循环为无并联电阻充放电循环,剩余11次为并联表1中不同阻值的充放电循环。16次循环的充电电压-时间曲线如图2所示。
由于充放电设备精度较低、实验过程中存在不可控因素如抖动等问题,导致充电电压-时间曲线含有微量噪声,因此本文使用多分辨率小波降噪对
16次循环充电电压-时间曲线进行降噪处理,降噪后的曲线如图3所示。图4为并联电阻阻值为3 Ω时的充电电压-时间曲线局部放大降噪前后对比图。显然,降噪后的曲线更平滑,符合充电过程中的真实电压变化情况,说明该方法能够有效降低曲线噪声。
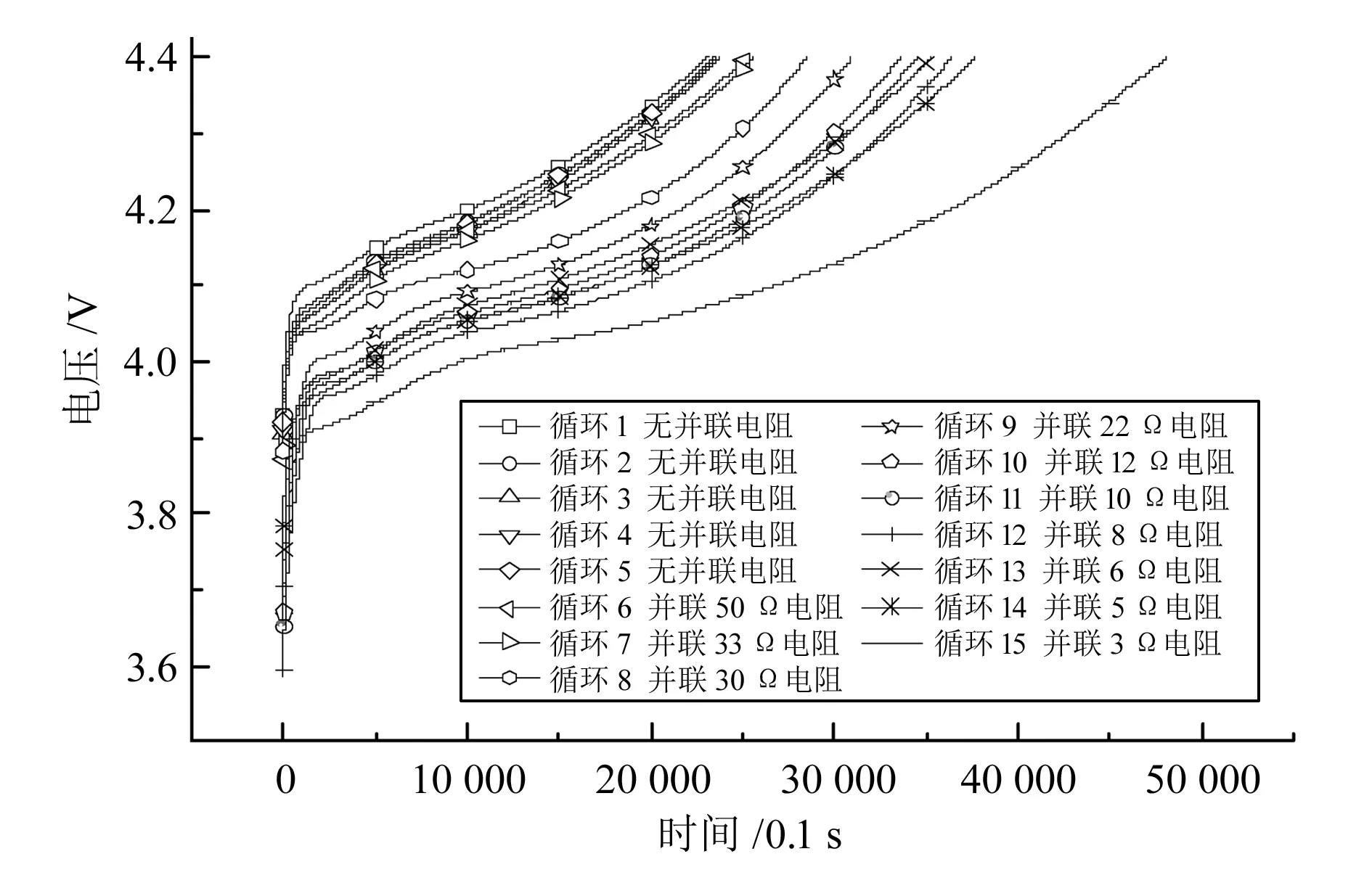
图3 锂离子电池充电电压-时间曲线

图4 锂离子电池充电电压-时间局部曲线降噪前后对比
由图3可知,当并联的电阻阻值越小,电压曲线的差异越大,说明很好地模拟了不同程度内短路的发生,但是这些曲线仍然纠缠在一起,不利于早期特征的提取。为了量化曲线间的差异,本文使用动态时间规整算法求得曲线间的最短规整路径距离作为故障预警特征,计算各充电循环充电电压-时间曲线(首次充电循环除外)与首次充电循环充电电压-时间曲线的最短规整路径距离。为了便于数值的展示与比较,令首个所求值放大为1,其余所求最短规整路径距离进行同比例放大,如图5所示。
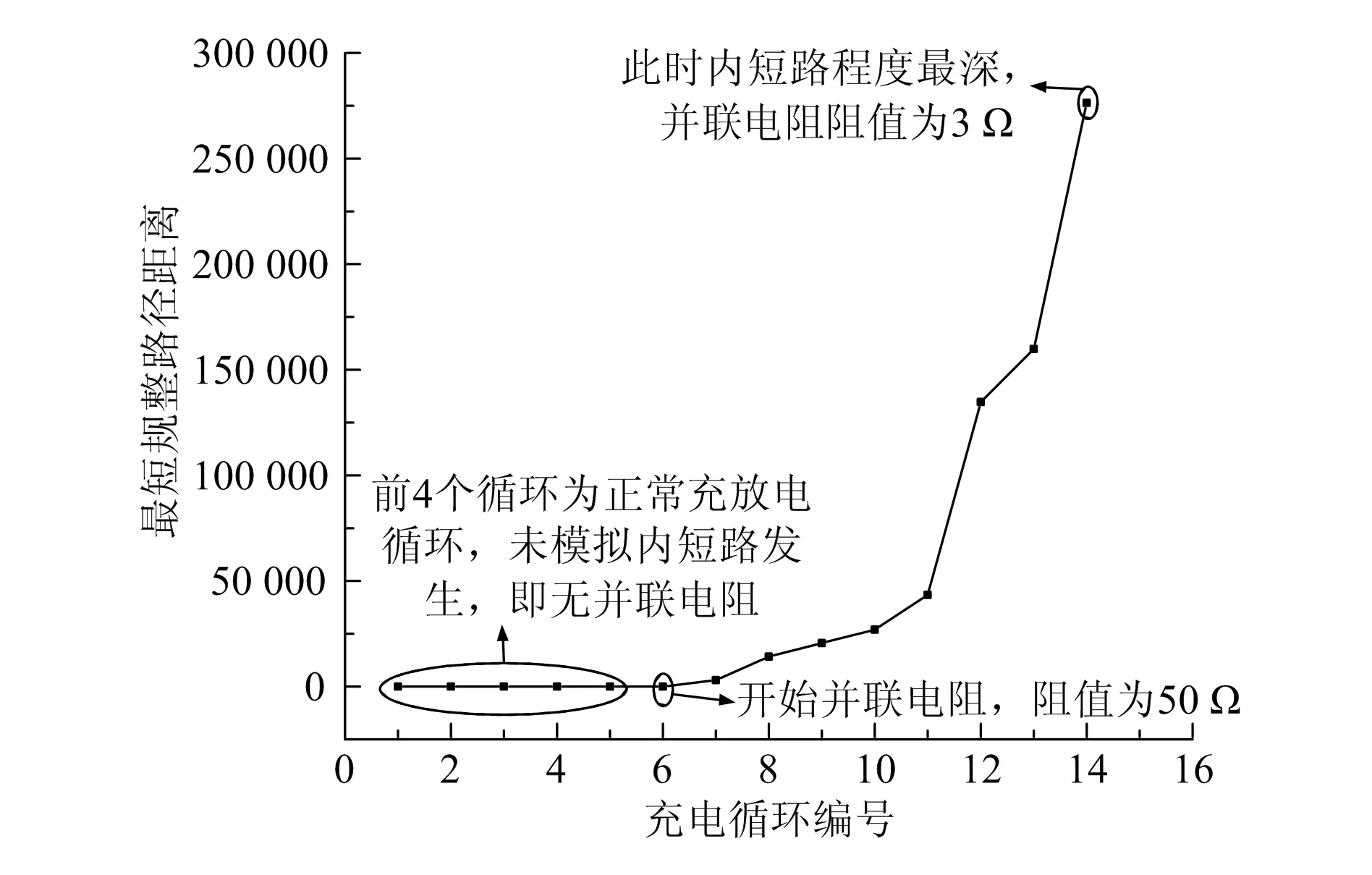
图5 各充电循环充电电压-时间曲线与 首次循环充电电压-时间最短规整路径距离
由图可知,4个未并联电阻的充电循环与首次充电循环的充电电压-时间曲线的最短规整路径距离极小,分别为1.00,7.27,5.19,2.22,曲线相似程度较高,未发现明显内短路故障特征。之后随着并联电阻阻值减小,自放电电流逐渐增加,内短路程度愈发加深,与首次充电循环曲线间的最短规整路径距离陡增,从并联电阻阻值50 Ω时的16.56上升至并联3 Ω时的276 322.92,曲线间相似程度显著降低,内短路故障特征愈发凸显。对于型号为BLP621的锂离子电池,其内短路故障报警阈值即为实验所得276 322.92。对于其他各种类型不同参数的锂离子电池,可同样使用本文提出的小波降噪-动态时间规整方法确定其对应的报警阈值,实现内短路故障诊断。由此可知,该方法能够有效地提取出早期的锂离子电池内短路故障特征,基于曲线相似程度预测出内短路故障程度,以并联电阻阻值为3 Ω时所求的最短规整路径距离作为报警阈值,实现有效的实时在线故障预警。
5 结束语
本文提出的基于小波降噪-曲线相似程度的锂离子电池内短路故障诊断方法,通过多分辨率小波降噪方法剔除噪声,提高了预测准确性;通过动态时间规整算法计算曲线相似程度,能够有效提取故障早期特征。实验结果表明,所设阈值能够有效地完成锂离子电池内短路故障提前预警,极大提升锂离子电池使用过程中的安全性和可靠性,避免重大安全事故的发生。
