基于EEMD与HHT的无转速计阶比分析方法

王 平，尹少平，贾护民，王灵梅

(1.山西大学绿色能源与电力智能控制研究所，山西 太原 030013) (2.青海绿电电力运维技术有限公司，青海 西宁 810001)

风力发电机组齿轮箱的振动信号随风速的波动呈现出非线性、非平稳性的特征，无法及时有效地识别提取，从而增大了故障识别的难度。在这种形势下，进行精确的故障诊断是当前风电机组运维工作的重要任务。

在风力发电机组变工况状态下，对齿轮箱振动信号直接进行快速傅里叶变化(fast Fourier transform,FFT)频谱分析可能会导致谱线中出现“谱线混淆”，难以识别故障特征频率。由于硬件阶比分析[1]与计算阶比分析方法中所用到的设备和检测装置可能会长期受到现场设备及运行环境的巨大影响和强度制约，因此很多专家学者转向无转速计阶比分析方法的研究中，并取得了一定的研究成果。其中，吕建新等[2]利用阶比分析与总体平均经验模式分解相结合的方法，对角域稳态信号进行集合经验模态分解(ensemble empirical mode decomposition,EEMD)，并对IMF分量进行分析，实现了对轴承故障的识别。杨志坚等[3]针对故障检测进行了大量的研究，基于能量重心法来获得信号的瞬时频率，利用瞬时频率获取信号的转速信息，并对信号进行阶比分析。金阳等[4]设计了零相位跟踪滤波方法，其优势主要体现在如下方面：首先降低滤波器边界对于信号的不利影响；其次是可以实现旋转机械信号转频。郭瑜等[5]重点针对无硬件设施进行了阶比分析，在此过程中采用了瞬时频率估算技术。徐亚军等[6]提出了基于线性调频小波路径追踪的阶比多角度形态学解调的分析方法，实现了对轴承的非稳态信号的故障诊断。

由于传统的时频分析方法对于非稳态、非线性的振动信号具有严重局限性，因此信号处理过程中存在严重的模态混叠现象，无法及时准确地提取有效故障信息。针对这一问题，本文提出了基于EEMD和希尔伯特-黄变换(Hilbert-Huang transform,HHT)相结合的无转速计阶比分析方法，并对该方法的实现与实际应用做了具体的阐述，实现了在无转速计的情况下，对变工况的齿轮箱振动信号提取精确的故障信息。

1 阶比定义

对于风电机组齿轮箱来说，其振动响应中所包含的信息会根据转速的变化而变化。阶比(order)定义如下：

(1)

阶比I的计算公式为：

(2)

式中：f为振动频率，Hz；n0为转速，r/min。

阶比域中，采样阶比Osample可以定义为：

(3)

式中：Δθ为常数，即两个采样点参考轴旋转的角度大小。

奈奎斯特阶比Onyquist定义为：

(4)

阶比分辨率ΔO定义为：

(5)

式中：Omax为最大分析阶次；N为角域重采样点数。

Δθ满足如下条件：

(6)

2 无转速计阶比分析过程

2.1 EEMD分解步骤

1)首先在原始信号x(t)中添加白噪声kσxn(t)，由此可以得到信噪混合体X(t)：

X(t)=x(t)+kσxn(t)

(7)

式中：k为比例系数；σx为标准差；n(t)为经过归一化处理之后的白噪声。

2)对X(t)进行经验模态分解(empirical mode decomposition,EMD)，得出单分量IMF的组合：

(8)

式中：Cj为加入白噪声后分解得到的第j个IMF；rm为残余函数，代表信号的平均趋势。

3)重复步骤1)和步骤2)，每次加入不同的白噪声ni(t)，得到信号Xi(t)：

Xi(t)=x(t)+kni(t)

(9)

将信号Xi(t)分解为IMF分量形式：

(10)

式中：Ci,j为第i次加入白噪声后分解得到的第j个IMF；ri,m为分解筛除m个IMF后的信号残余分量。

4)重复N次，并对各个IMF求平均得到EEMD分解后最终的IMF，即：

(11)

式中：Cj(t)为EEMD分解的第j个IMF。

2.2 瞬时频率的提取

利用时频分析进行瞬时频率估计从而提取转速时，需要对数据进行归一化处理：

1)将采集到的振动信号进行EEMD分解，最终得到有限个无模态混叠的IMF单分量IMFCj(t)。

2)对IMFCj(t)取绝对值后找出其所有的极大值点。

3)对极大值点使用样条函数构造出样条包络数ei(t)。

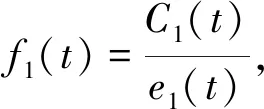
6)基于Teager能量算子计算调频、调幅分量，然后通过HHT对能量包络求取瞬时频率。

2.3 角域重采样

1)利用三阶多项式拟合瞬时转频fr(tn)：

(12)

式中：a，b，c，d分别为各阶拟合系数；tn为信号采样时间。

2)已知x(tn)表示振动信号，需要对最大分析阶次Omax进行确定，Omax应该是采样阶次的一半。

3)针对角度增量Δθ进行计算，公式为：

(13)

计算重采样后信号的长度L：

(14)

式中：t0为初始时刻。

4)计算等角度重采样的各鉴相时标θn：

(15)

其中n=1,2,…,L,通常情况下，t0=0。

5)根据式(16)求得的θn，对振动信号x(tn)进行插值处理。

(16)

式中：x(θn)为角度域重采样信号。

3 方法验证

3.1 仿真信号分析

本文中将信号表示为如下形式：

x=sin(2πt2)+sin(4πt2)+sin(6πt2)+sin(10.2πt2)+0.8η(t)

(17)

式中：η(t)代表的是高斯白噪声(η(t)～N(0,1))，其一阶转速为n(t)=2×60t2，对应的瞬时频率(instantaneous frequency,IF)为nIF(t)=2t2。结合式(17)所表示的仿真信号，来完成仿真测试的过程。其中信号的采样频率f=256 Hz，信号的采集周期t=8 s。基于仿真获得的时域波形如图1所示，从图中可以明显看出此信号为典型的非平稳信号，其中夹杂着严重的噪声。对信号直接进行傅里叶变化会出现频谱杂乱的现象，导致故障信息显示模糊，如图2所示。

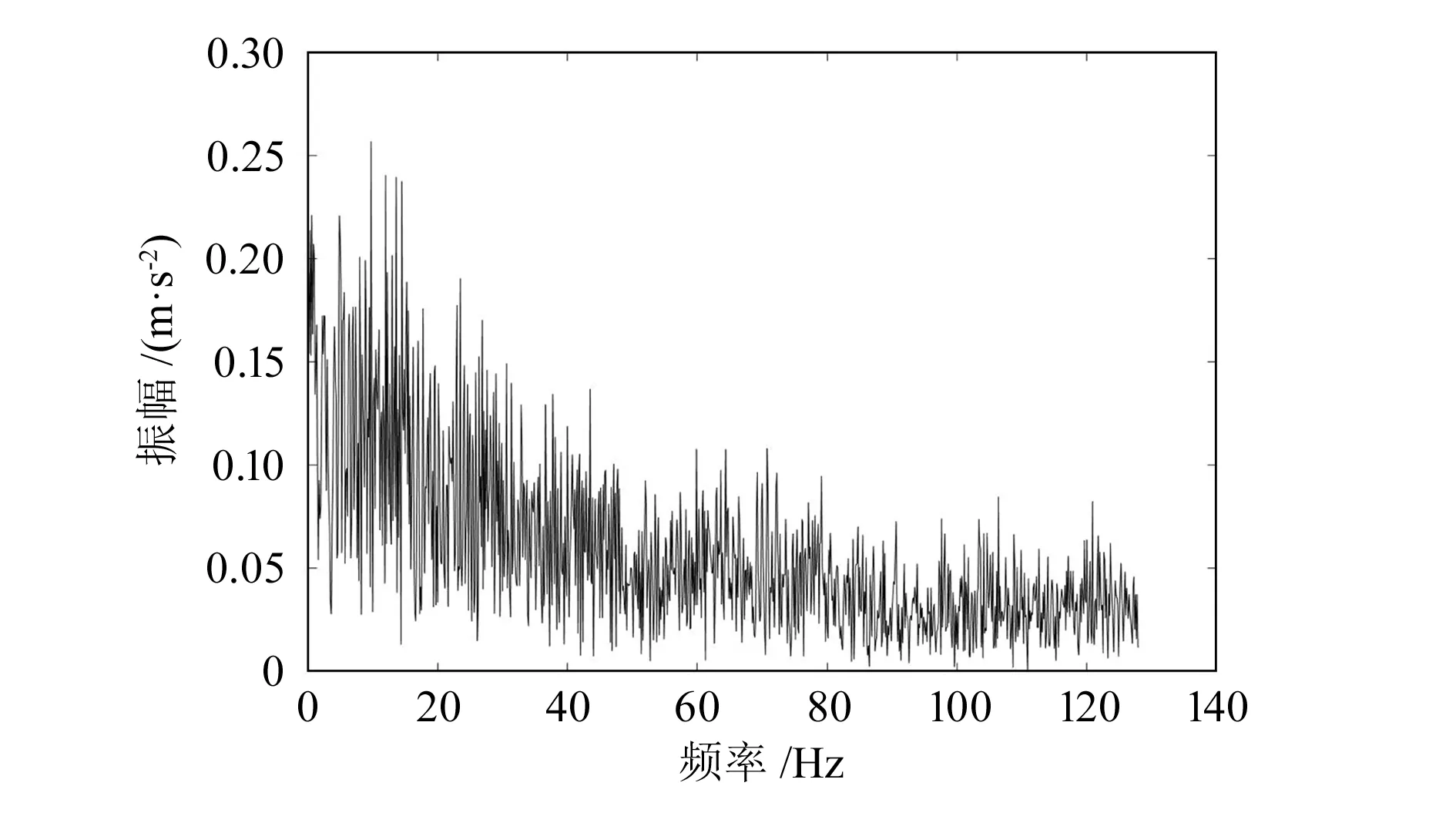
图2 原始信号的FFT图

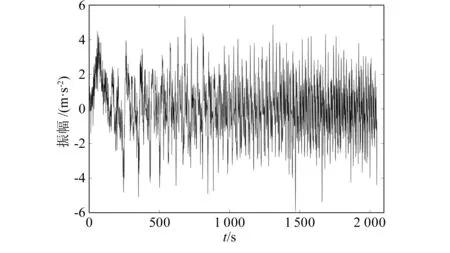
图1 仿真信号时域波形

首先进行EEMD分解，设置信号中添加的高斯白噪声标准差σ=0.5、添加噪声次数N=100，获得对应的IMF分量(12个)，其中IMF1为原始仿真信号，其他均为EEMD分解之后得到的IMF分量，具体结果如图3所示。

图3 EEMD分解得到的IMF分量

用归一化方法对IMF分量进行筛选，选出敏感分量IMF的调频分量，并计算其瞬时频率进行曲线拟合后得到瞬时转频，如图4所示。根据HHT估计后的转频曲线计算重采样时刻，并根据计算好的鉴相时标对原始仿真信号进行等角度间隔采样，结果如图5所示。

图4 HHT估计的转频曲线

图5 重采样信号

将得到的角域数据进行FFT，得到的阶比谱如图6所示。其中基频部分含有较多的能量，并且图中还有2阶、3阶、5阶等高阶频率明显存在，频谱的形状类似于“枞树形”，所以与故障信号特征保持了较高的一致性，由此证明了该方法的应用效果。

图6 阶比谱

3.2 工程实例分析

利用实验室自主研发的振动监测仪，选取山西某风电场所采集的1.5 MW双馈风力发电机的振动数据进行分析。振动监测设备的信号采集频率为51 200 Hz，信号采集周期为1.28 s。

3.2.1正常信号分析

图7为正常信号的分析结果，其中图7(a)为正常信号的时域波形，图7(b)为振动信号经过FFT变化后得到的频谱图，图7(c)为采用本文研究方法处理之后得到的阶比谱图。通过图7(b)与图7(c)的对比可以清楚地看出信号经过FFT变化之后出现“频率模糊”现象，并且在阶比谱基频部分的信号冲击不显著，故障信号成分无显现。

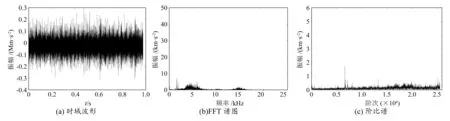
图7 无故障振动信号

3.2.2故障信号分析

图8为故障信号的分析结果，其中图8(a)为正常数据的时域波形，图8(b)为振动信号经过FFT变化后得到的频谱图，图8(c)为振动信号处理后得到的阶比谱图。根据图8(b)与图8(c)的对比可以清楚地看出信号经过FFT变化后出现“频率模糊”现象，与正常数据分析阶比谱相比在基频阶段出现明显的信号冲击，且故障振动信号成分表现明显，再次证明了本文所提方法的有效性。

图8 故障振动信号

4 结束语

本文在对风力发电机组齿轮箱振动信号的分析过程中，考虑到信号的非平稳、非线性的特点，提出了一种无转速计阶比分析的方法。采用EEMD与HHT相结合的方法，提取信号中的瞬时频率，并利用瞬时频率将信号转换为角域信号，提高了故障的分辨率与精确度。对仿真和实测信号的实验结果证明了本文所提方法的有效性与实用性。本文的研究对提升风力发电机组齿轮箱的故障诊断具有重要的实用价值，可在风电场大力推广使用，对提高风电场的运维效率具有较大的作用。