个体化全膝关节置换骨肌多体动力学模型的适用性评估

李宏伟,刘 峰

(中北大学机械工程学院，山西 太原 030051)

全膝关节置换术被认为是治疗终末期骨性膝关节炎的有效手段。近年来，我国膝关节置换患者群体急剧增加，并呈现出年轻化趋势[1]。研究膝关节假体磨损性能和设计具有更长使用寿命的膝关节假体成为目前主要的研究趋势。研究表明，准确获取膝关节假体体内力学信息对于评估膝关节假体磨损寿命、改善膝关节假体设计和提高假体摩擦学性能具有重要意义[2]。

基于膝关节挑战赛公开数据集[3]，众多学者致力于开发个体化骨肌模型，用于预测膝关节假体体内力学信息，但是个体化骨肌模型的建立通常需要复杂的建模流程以及专业的算法和医学知识，并不利于实现广泛临床应用。AnyBody生物力学建模软件提供了具有完整人体肌肉配置的通用模型，并允许用户进行个性化设置，具有可观的临床应用潜能。Marra等[4]在AnyBody中应用Andersen等[5]提出的依赖于力的运动学(force-dependent kinematics，FDK)建模方法初步建立了个体化全膝关节置换骨肌模型建模框架，Chen等[6-7]对Marra等[4]提出的建模框架进行了正常步态和右转步态下的验证，初步展示了该建模框架的准确性。但是，目前尚不清楚该建模框架是否具有广泛适用性，特别是对于下蹲和坐立这两种日常运动形式。因此，为实现个体化骨肌模型的广泛临床应用，对其进行多种运动形式下的适用性研究是十分有必要的。

基于以上目的，本文在AnyBody生物力学建模软件中对4位膝关节置换患者建立了个体化全膝关节置换骨肌多体动力学模型，分别对下蹲和坐立运动进行模拟仿真，通过与实验测量数据对比来评估所建骨肌模型的准确性和适用性。

1 材料与方法

1.1 患者实验数据

选取来自近四届膝关节挑战赛公开数据集中的4位膝关节置换患者为研究对象[3]，评估个体化骨肌模型在下蹲(站立—下蹲—站立)和坐立(坐姿—站立—坐姿)两种运动形式中的适用性，其中每位患者进行3次下蹲运动和1次坐立运动。所研究的4位患者信息见表1，其涵盖了不同性别、不同侧膝关节以及不同假体类型，具有一定的代表性。此外，公开数据集还提供了每位患者的术前和术后下肢CT(computed tomography)图像、膝关节假体几何模型，以及下蹲和坐立运动过程中的运动学捕捉数据、通过测力板测得的地面反作用力以及通过内置电子化膝关节假体所测量的胫股关节接触力数据。

表1 选用的膝关节置换患者信息

1.2 个体化膝关节置换骨肌多体动力学模型

本文在生物力学建模软件AnyBody v.7.2所提供的全身通用模型的基础上，建立个体化全膝关节置换骨肌多体动力学模型。其中，通用模型由上肢骨骼模型(由腰部区域、刚性躯干、颈部、头部和双臂组成)和TLEM 2.0通用下肢骨肌模型(由骨盆、左右侧股骨、髌骨、胫骨、腓骨、距骨和足骨组成，每条腿分布169条Hill型肌肉束)构成[8]。

1.2.1基于站立姿态的模型建立

如图1所示，首先基于CT重建骨骼对通用下肢骨骼进行个体化缩放[4,6]，完成患者术前下肢模型的建立；然后根据术后CT图像进行膝关节置换模拟，将术后截骨和假体几何模型导入到对应术前骨骼上，并对下肢各关节进行关节中心的确定：髋关节设定为具有3个旋转自由度(DOF)的球面关节，而胫股关节、髌股关节、踝关节和距下关节均设定为单自由度铰链关节[9-10]。髌股关节由通过8个与股骨部件滑车槽相切球体的球心所拟合的圆确定，其旋转中心设定为该圆的圆心，旋转轴为过该圆心且垂直于拟合圆的垂线。踝关节和距下关节分别通过在其关节面内侧和外侧拟合两个球体进行确定，其中关节轴为两球心连线，旋转中心为连线中点[10]。

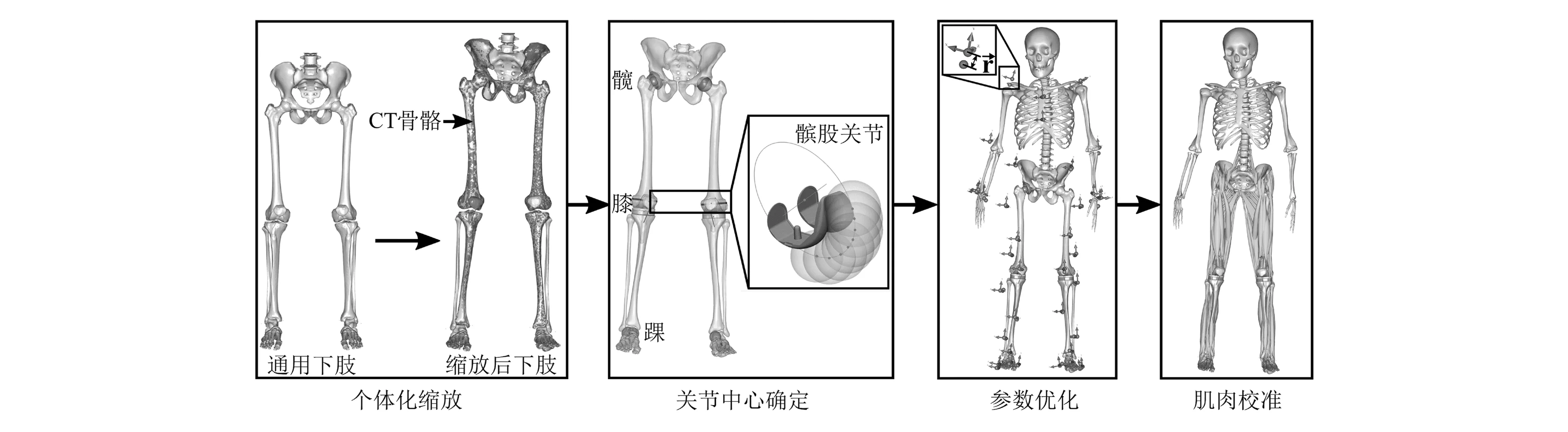
图1 个体化全膝关节置换骨肌模型建模流程

对于缺乏CT图像而无法进行个体化缩放的通用上肢骨骼模型，通过身高-体重-脂肪缩放定律和Andersen等[11]提出的基于皮肤表面标记点位置的参数优化方法来进行优化缩放。该方法通过使用最小二乘法减小模型中内定标记点与皮肤表面标记点之间的距离r来完成骨骼的缩放和关节中心以及屈曲轴的确定。同时，参照文献[12]完成下肢主要肌肉群的肌肉强度校准。

1.2.2逆向动力学求解

在逆向动力学求解中，应用FDK方法实现膝关节的12-DOF运动(包括胫股关节的6-DOF运动和髌股关节的6-DOF运动)。同时，为了保持膝关节假体的运动稳定性，建立了20条一维非线性弹性单元来代表术后韧带(图2)，各韧带遵循以下力-位移关系[13]：

图2 个体化全膝关节置换骨肌模型膝关节韧带配置

(1)

ε=(l-l0)/l0

(2)

l0=lr/(εr+1)

(3)

式中：f(ε)为韧带所受拉力；k为韧带刚度；ε为当前韧带应变；ε1为许用应变，设定为0.03；l为韧带长度；l0为韧带零载荷长度，其与站立姿态下的韧带初始长度lr和参考应变εr相关。韧带刚度k和参考应变εr参考相关文献中的实验测量数据[14]。

在假体间设立刚体对刚体类型的接触对来计算膝关节假体接触力。其中，接触力Fc是通过计算两个接触面之间的相交体积Vc并乘以压力模量P(4.65×1010N/m3)求得，其计算公式为：

Fc=PVc

(4)

在运动模拟过程中，首先进行运动学分析，前文中基于站立姿态建立的模型中所有内定标记点将跟随患者真实运动过程中的皮肤表面标记点进行运动，带动骨肌模型完成整个运动过程，同时计算出运动过程中人体各关节的运动角度，用于驱动逆向动力学分析中各关节运动。在逆向动力学分析阶段，地面反作用力、脚部接触时的力矩和运动学分析获得的运动关节角度将一同作为逆向动力学分析的输入，通过式(5)所示的三次多项式肌肉募集方程完成最终的逆向动力学求解。考虑到AnyBody中某些肌肉被细分为多束，在肌肉募集方程中引入肌肉束体积因子Vi[4,6](对于未细分肌肉，其为肌肉体积；对于细分肌肉，其为每束肌肉体积，由该肌肉体积除以细分肌肉数量求得)。

(5)

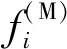
1.3 模拟结果评估

为准确评估模拟结果，将模型预测结果与实验测量数据进行了对比分析，并与文献[15]、[16]的预测结果进行了对比验证。其中，模型预测值和实验测量值均使用线性插值方法将其缩放到0～100%步态周期内，并使用皮尔逊相关系数p(Pearson correlation coefficient)和均方根误差RMSE(root mean square error)对两者间的差异进行量化。

2 结果与讨论

表2为4位膝关节置换患者在下蹲和坐立运动形式下模型预测的胫股关节内侧、外侧和总体接触力与实验测量数据之间的差异对比结果。与实验测量数据相比，模型预测结果取得了较高的相关性和较低的均方根误差：在下蹲运动中，模型预测的胫股关节接触力的均方根误差范围为67～225 N，相关系数范围为0.77～0.98；在坐立运动中，模型预测的胫股关节接触力的均方根误差范围为82～336 N，相关系数范围为0.55～0.97。总体来看，模型在4位患者的下蹲和坐立运动中所预测的胫股关节接触力的均方根误差范围为67～336 N，相关系数范围为0.55～0.98。所建模型在4位患者的下蹲和坐立运动形式中显示出良好的适应性，并保持了较高的膝关节假体接触力预测精度。

表2 模型对于胫股关节接触力的预测精度

以患者4为例，图3展示了其在下蹲和坐立运动中模型预测的胫股关节总体接触力与实验测量数据的对比结果，其中图3(a)中的阴影部分为3次下蹲运动中的接触力分布范围，实线与虚线分别为3次下蹲运动中的模型预测与实验测量的接触力平均值。模型预测的胫股关节假体接触力曲线与实验测量力曲线呈现出相似的变化趋势，所建骨肌模型能够准确预测下蹲运动中假体接触力曲线的单个力峰值(出现在下蹲阶段)和坐立运动中假体接触力曲线的两个力峰值(分别出现在坐姿-站立阶段前期和站立-坐姿阶段后期)。特别地，对于患者4来说，模型在其坐姿-站立期间保持较高胫股关节接触力预测精度的同时，还合理地预测出其站立-坐姿期间的胫股关节假体接触力，如图3(b)所示。

图3 患者4不同运动中胫股关节假体总体接触力

与文献[15]、[16]的预测结果相比，本模型展现出更为准确的膝关节假体接触力预测能力。在Kebbach等[15]对患者3的下蹲运动模拟预测结果中，其预测的膝关节假体总体接触力的均方根误差为255 N，大于本模型预测结果的均方根误差(177 N)；在Asseln等[16]对患者1和患者3的下蹲运动模拟结果中，其预测的膝关节假体总体接触力的均方根误差为508～824 N，远大于本模型在下蹲运动预测结果中的最大均方根误差(225 N)，这进一步证明了本文所建个体化全膝关节置换骨肌多体动力学模型的准确性。

3 结束语

本文基于AnyBody生物力学建模软件对来自近四届膝关节挑战赛公开数据集中的4位膝关节置换患者进行个体化全膝关节置换骨肌模型建模，并分别在下蹲和坐立运动形式下进行模型验证，结果表明，所建个体化全膝关节置换骨肌模型在不同患者的下蹲和坐立运动形式下显示出良好的适应性，并保持了较高的膝关节假体接触力预测能力，为进一步实现个体化骨肌模型广泛临床应用提供了理论依据和研究平台。