复合材料层合板偏心压缩渐进损伤研究

2021-06-15袁坚锋

机械设计与制造工程 2021年5期

袁坚锋

(中国商飞上海飞机设计研究院，上海 201210)

飞机在空中飞行时，复合材料机翼上壁板受到压缩和弯曲载荷的联合作用，即偏心压缩效应。在压、弯载荷同时作用下，层合板更容易发生破坏，因此研究偏心压缩载荷作用下复合材料层合板的失效显得尤为重要。为预测复合材料层合板的损伤扩展和极限强度，学者们在复合材料结构失效分析中引入了渐进损伤分析方法[1-4]。渐进损伤分析方法包括应力求解、失效分析和材料属性退化三部分，其中应力分析的非线性平衡方程求解可由有限元软件完成，而复合材料本构方程的建立和应力更新、材料失效准则的确定以及损伤材料属性退化方案的研究等大部分的研究工作需要人工完成。

文献[5]～[8]基于复合材料渐进损伤分析模型采用基于经典层合板理论的二维有限元法进行应力求解，但无法较好地反映层合板三维效应和铺层之间的相互作用。后来，一些研究人员在分析复合材料层合板螺栓连接失效问题时建立了三维渐进损伤分析模型，并采用三维有限元法进行应力求解。还有一些研究模型[9-10]采用连续介质损伤力学中的内部损伤状态变量表征材料的损伤状态，不同损伤模式采用不同损伤状态变量表示，损伤状态变量由材料的临界断裂应变能释放率确定。王跃全等[11]建立了复合材料渐进损伤分析的三维模型，该模型采用指数形式的应变软化率表示材料的损伤扩展，有效地反映了复合材料层合板的层间损伤。

本文通过对复合材料层合板损伤本构方程的推导，采用考虑剪切非线性的三维Hashin准则对复合材料层合板进行三维渐进损伤有限元分析，讨论了损伤材料性能退化方案，引入与材料损伤模式相对应的损伤变量表征材料的损伤状态，并对复合材料层合板受偏心压缩载荷的行为与强度进行预测。

1 损伤本构方程

基于连续损伤力学，含损伤正交各向异性单层复合材料层合板的本构方程为：

σ=Cdε

(1)

式中：σ,ε,Cd分别为应力向量、应变向量和损伤后刚度矩阵，d表示损伤。

(2)

其中：

式中：Cij(i,j=1,2,3,…,6)为单层刚度分量；di(i=1,2,3)为垂直于各个主方向有效承载面积的减小比例，其值为0～1，di=0表示第i材料主方向无损伤，di=1表示第i材料主方向完全断裂。定义坐标方向1为单层复合材料面内平行于纤维的方向，2为面内垂直于纤维的方向，3为面外法方向。

2 材料失效准则

本文采用考虑剪切三维非线性Hashin准则，包括纤维在拉伸和剪切下的断裂、纤维压缩屈曲、基体在拉伸和剪切下的断裂、基体在压缩和剪切下的压溃、铺层间的分离及纤维-基体界面在压缩和剪切载荷下的断裂等失效模式，各失效模式如下：

纤维失效

(3)

基体失效

(4)

分层失效

(5)

纤维-基体剪切失效

(6)

式中：F1,F2,F3和F4分别为纤维、基体、层间和纤维-基体界面的损伤变量；XT,XC为纤维方向拉伸和压缩强度；YT,YC为横向拉伸和压缩强度；ZT,ZC为厚度方向拉伸和压缩强度；S12和S13,S23分别为一个面内剪切强度和两个面外剪切强度，其中下标1表示纤维方向，2表示横向，3表示厚度方向；α为非线性剪切常数；G12为面内剪切模量；G13为面外剪切模量；σ11为纤维方向应力；σ12为面内剪应力；σ13为面外剪应力；σ22为面内垂直纤维方向应力；σ33为面外垂直纤维方向应力。

3 材料退化方案

复合材料结构渐进损伤中的材料退化模型主要包括瞬间退化模型、线性退化模型[10]和指数退化模型[9]，如图1所示。

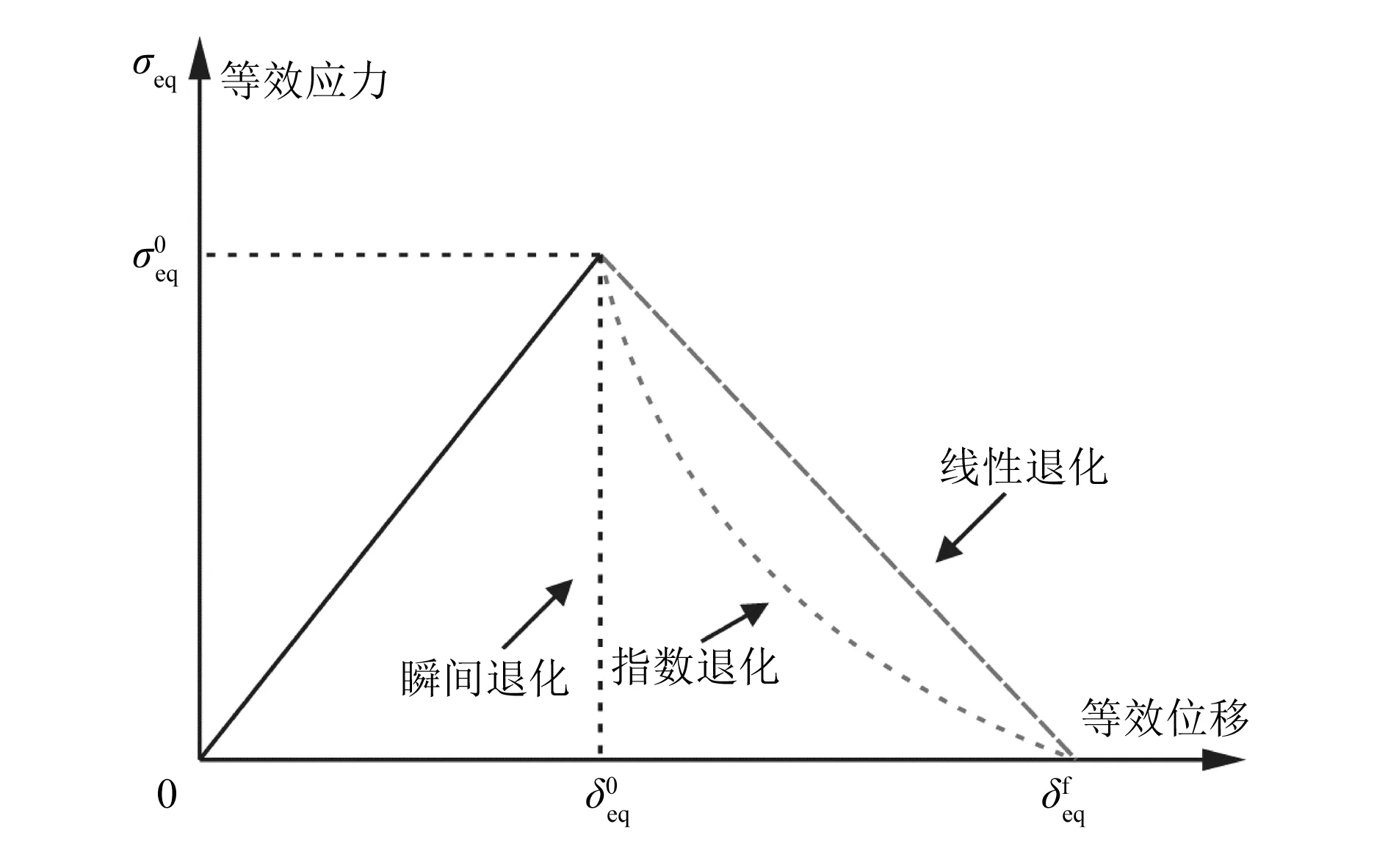
图1 复合材料渐进损伤退化模型

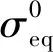
δeq,ij=εijLCi,j=1,2,3

(7)

式中：LC为单元的特征长度；εij为应变分量。

极限等效位移定义为：

(8)

(9)

指数退化模型的损伤变量定义为：

(10)

(11)

(12)

参照文献[12]的形式定义损伤变量d4为：

(13)

式中：Gc,1，Gc,2和Gc,3分别为材料3个方向上的断裂能量释放率。

(14)

4 复合材料层合板偏心压缩模拟

4.1 复合材料层合板偏心压缩试验

试验件尺寸为125 mm×25 mm×5 mm，具体如图2所示，对试验件的夹持/加载端采用胶接的方式进行局部加强。试验件采用碳纤维增韧环氧树脂复合材料，加强片采用玻璃纤维环氧树脂复合材料，试验件的铺层为[45/02/-45/90/45/02/-45/0]S，共20层，总厚度为5 mm。

图2 试验件示意图

通过专用夹具夹持试验件，由试验机压头直接施加压缩载荷。通过专用夹具保证试验机载荷中线通过试验件横截面不同位置，形成偏心压缩，从而实现不同压弯载荷组合。

4.2 有限元模型

试验件和试验夹具采用C3D8R三维实体单元建模，在夹具与试验件加强片之间建立接触，固定下方夹具并对上方夹具施加均匀位移载荷以模拟试验加载情况，如图3所示。通过调整夹具与试验件装配的相对位置控制载荷的偏心率，建立偏心率e为0，0.25和0.50共3种有限元模型，采用ABAQUS/Standard联合用户定义材料子程序UMAT进行分析。

4.3 有限元模拟结果及与试验对比分析

通过ABAQUS/Standard计算得到的3种偏心率下复合材料层合板名义应力-应变曲线如图4所示，由图可以看出，3条曲线的斜率和最高点随偏心率增大而减小，即3块试验件的刚度和强度随偏心率增大而减小，e为0时的对心压缩强度明显高于e为0.25和0.50时的偏心压缩强度，为659.82 MPa；e为0.25和0.50时的偏心压缩强度相差不大，分别为420.66 MPa和390.47 MPa。由此可见弯曲载荷会使试验件的强度大幅降低。

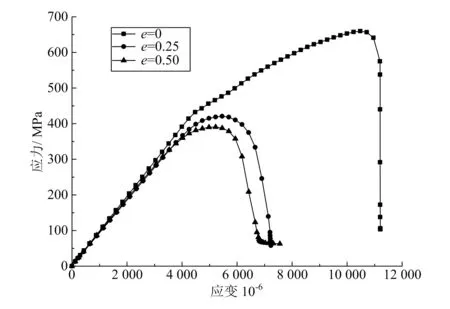
图4 不同偏心率下试验件名义应力-应变曲线

e为0时试验件的损伤如图5所示。由图可以看出，基体损伤和分层损伤较严重，主要发生在45°和90°铺层；而纤维损伤和纤维-基体剪切损伤变量均未达到1，表示材料尚未破坏。有限元模型在夹持端根部基体断裂并在模型内部出现大量分层，试验件最后的破坏模式为压缩和分层失效。

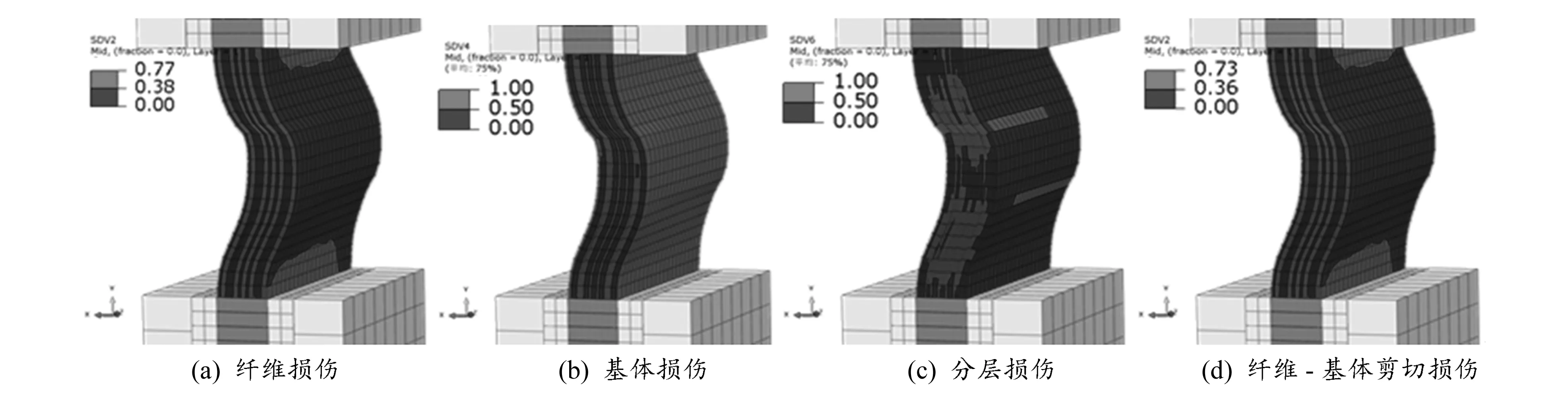
图5 e为0时试验件损伤示意图

e为0.25时试验件的损伤如图6所示。由图可以看出，试验件在弯曲和压缩载荷作用下发生弯曲变形，基体损伤和分层损伤较严重，基体损伤沿试验件中心呈对称分布，分层损伤集中在试验件中部；纤维损伤和纤维-基体剪切损伤也呈对称分布且损伤变量均未达到1。试验件由于局部弯矩导致截面内部产生分层，分层扩展使试验件失去整体性，最终发生弯曲失效。