3 500 kN立式摩擦焊机导柱的有限元模拟与优化设计
2021-06-15吴永强李丽琼
吴永强,辛 舟,李丽琼
(兰州理工大学机电工程学院,甘肃 兰州 730050)
3 500 kN立式专用摩擦焊机是电解铝阳极钢爪的专用焊接设备,导柱部件是摩擦焊机的重要部件,是整个机器中承受力较大的部件[1]。国内外对机床导柱有过很多研究,文献[2]应用Pro/E三维建模和ANSYS有限元分析相结合的方法完成了对TH65100型立柱式导轨的应力和变形情况分析与优化改进,该研究为提高机床的加工精度和立柱式导轨的结构特性提供了依据。文献[3]、[4]应用有限元分析软件ANSYS对加工中心的立柱式导轨内部3种不同的肋板结构分别对应的静、动态特性进行了对比分析,优选出最佳的肋板结构形式。本文中导柱的强度与刚度直接影响摩擦焊接质量,因此对导柱部件进行有限元模拟与优化设计就显得很有必要。
1 有限元模拟
1.1 有限元模型的建立
摩擦焊主机主要由导柱、顶锻箱、机座、夹具、液压缸、主轴箱、电机等七大部件构成,如图1所示。
由于导柱模型为对称结构,因此取该模型的1/4用于分析[5],如图2所示。导柱所采用的材料为16Mn,泊松比μ为0.31,质量为1 530.3 kg,屈服极限为345 MPa,导柱部件的弹性模量E为212GPa。因为导柱部件结构比较复杂、倒角比较多,所以用自由网格划分方法来处理导柱模型,网格生成后节点数量为42 960、单元总数为22 576。
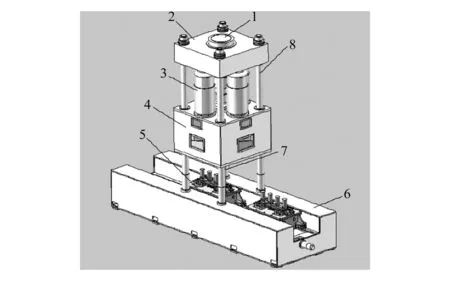
1—液压缸;2—顶锻箱;3—电机;4—主轴箱;5—钢爪夹具;6—机座;7—钢棒夹具;8—导柱图1 摩擦焊机三维模型
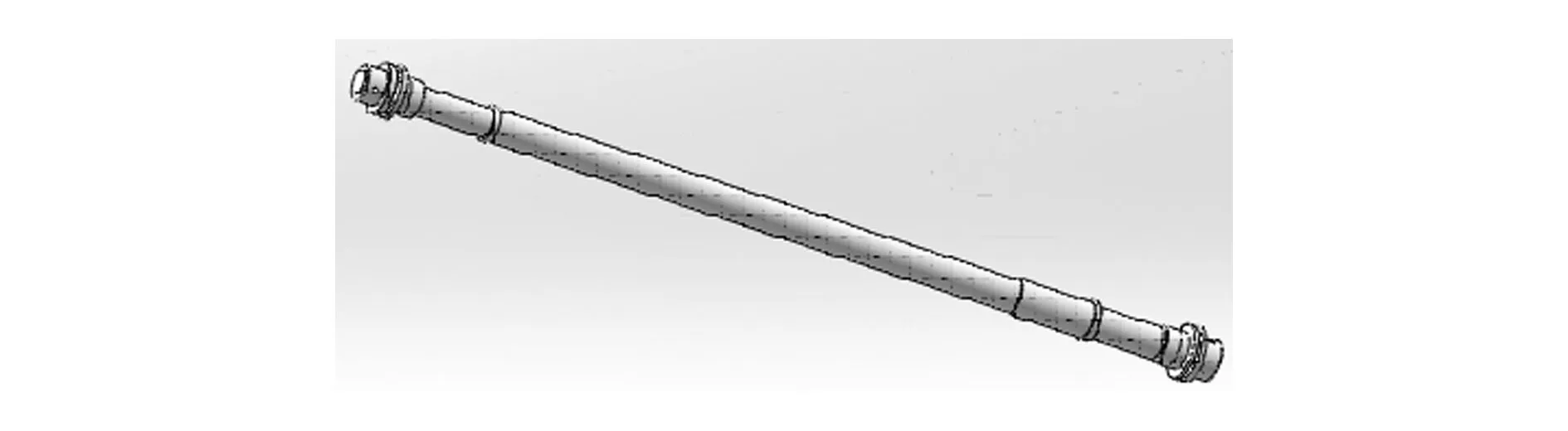
图2 导柱部件三维模型
1.2 数值模拟结果分析
在导柱部件的下端面处施加固定约束,约束其所有自由度。如图3、图4所示,导柱部件的最大应力为71 MPa,出现在下导柱圆套处,由于材料的屈服强度为345 MPa,因此满足强度要求。导柱部件的最大综合变形为0.8 mm,导柱部件的最大变形发生在上导柱螺母处,因此可以通过改变轴径进而减小导柱部件的总变形。图5的模拟结果显示导柱部件安全系数为4.86,说明其还有较大的结构优化改进余地[5]。
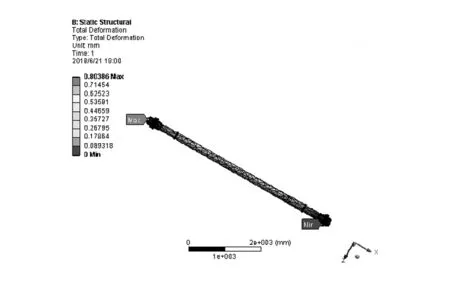
图3 导柱部件总变形云图
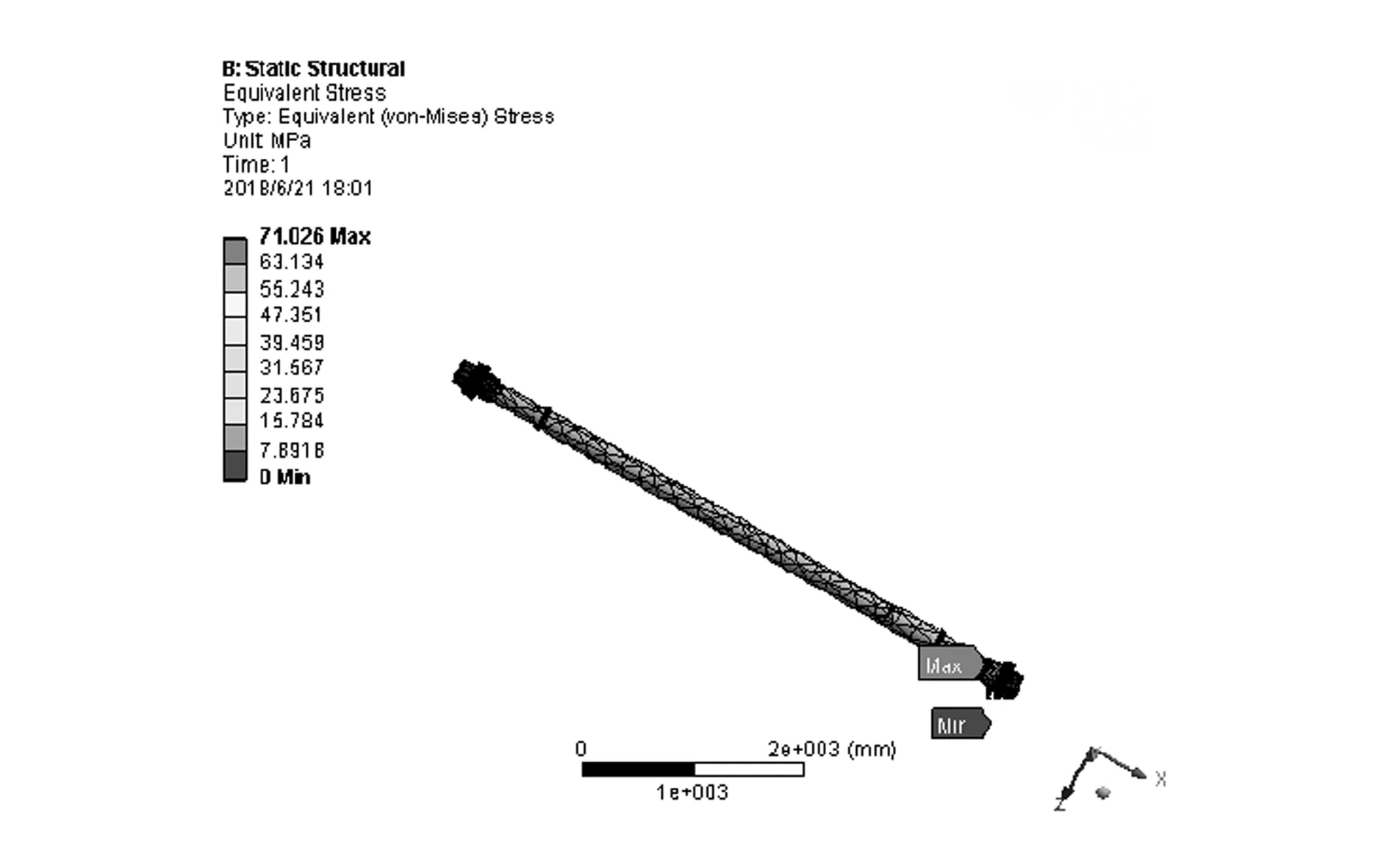
图4 导柱部件应力云图
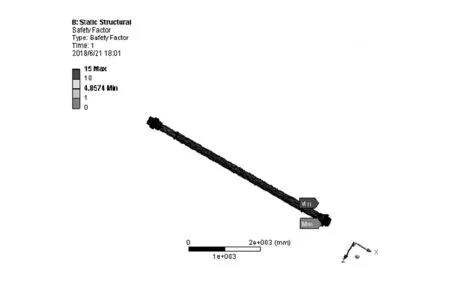
图5 安全因子
2 导柱部件拓扑优化
2.1 拓扑优化的基本原理
拓扑优化[5-6]指的是在给定的设计范围内寻找承受载荷的最优材料分布。现在常用的结构拓扑优化方法有变密度法、均匀化法和变厚度法。ANSYS中拓扑优化采用的是变密度法。变密度法[7]假想材料参数(如泊松比等)和其材料密度之间存在一种线性或非线性关系,当在ANSYS软件中完成对连续结构的网格划分后,其每一个网格单元的密度都是1。假定材料密度ρ与材料弹性模量E两者间的关系是:
(1)
式中:E0为实际所用材料的弹性模量;μ0为实际所用材料的泊松比;α为惩罚因子,使得单元密度向0和1两端汇聚。
拓扑优化变密度法[7-8]的数学模型为:
(2)
式中:Compliance为柔度;Weight为结构优化后的材料质量;fi和ti分别为作用在初始结构上的体积力和面积力;xi为网格单元的变形值;ε为材料密度的下限;V0为给定的初始结构材料质量的上限;Ω为体积域;Γ为面积域;μi为泊松比;Δ为优化时指定省去的材料百分比;j1,j2,… ,jn为优化后伪密度仍为1的单元号。
2.2 导柱的拓扑优化
设置减小质量20%为目标,计算结果如图6所示,需要去除的部分用Remove表示,边缘部分用Marginal表示,这部分可以留下也可以不留下,需要留下的部分用Keep表示。为了方便加工制造,对结构进行修改时可以与优化结果不完全一致[5],如仅对导柱部件上下锥套间的部分进行中空处理。

图6 拓扑优化分析
3 导柱的六西格玛优化
3.1 六西格玛设计技术
六西格玛设计(DFSS)技术[9]以6个标准误差为理论基础,假定不确定性输入变量(如材料属性、几何尺寸、载荷等)的概率分布,分析输入变量不确定性对产品性能(应力、变形等)的响应,判断产品设计能不能满足六西格玛质量要求(1 000 000件中只有3.4件失效),并评测其可靠概率或失效概率。首先按照DesignXplorer优化设计过程进行分析,将上导柱螺母轴径X1、上导柱空心径X2、下导柱空心径X3、上导柱轴径X4、下导柱轴径X5设为输入变量,如图7所示,将导柱的质量、最大变形和等效应力作为输出参数;然后进行六西格玛设计,用中心复合设计法进行试验设计,各变量的分布类型都是正态分布,参数见表1;最后更新试验响应面和设计点,读取后进行结果的处理。
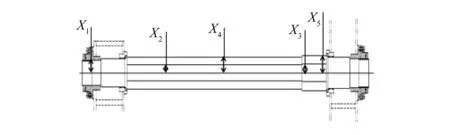
图7 参数化模型图
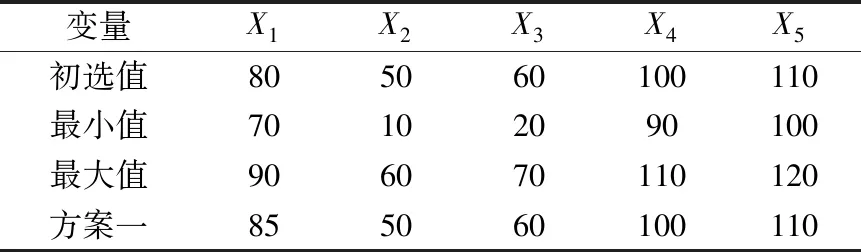
表1 变量参数值 单位:mm
3.2 优化结果分析
图8为设计变量对优化目标的灵敏度,从图8可以看出,质量主要与空心径有关,空心径越大质量越小,上导柱螺母轴径对变形为负影响。由图9可知,变形量随上导柱螺母轴径的增加而减小,随上导柱空心径的增大而增大,而下导柱空心径对于应力是正影响,下导柱轴径对应力为负影响。图10反映了等效应力随下导柱空心径和下导柱轴径的变化情况。
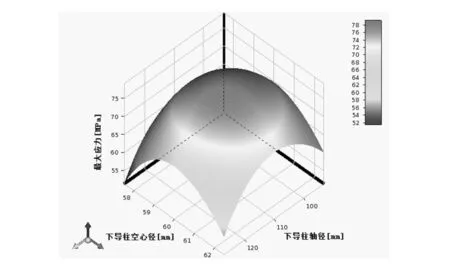
图10 应力响应面云图
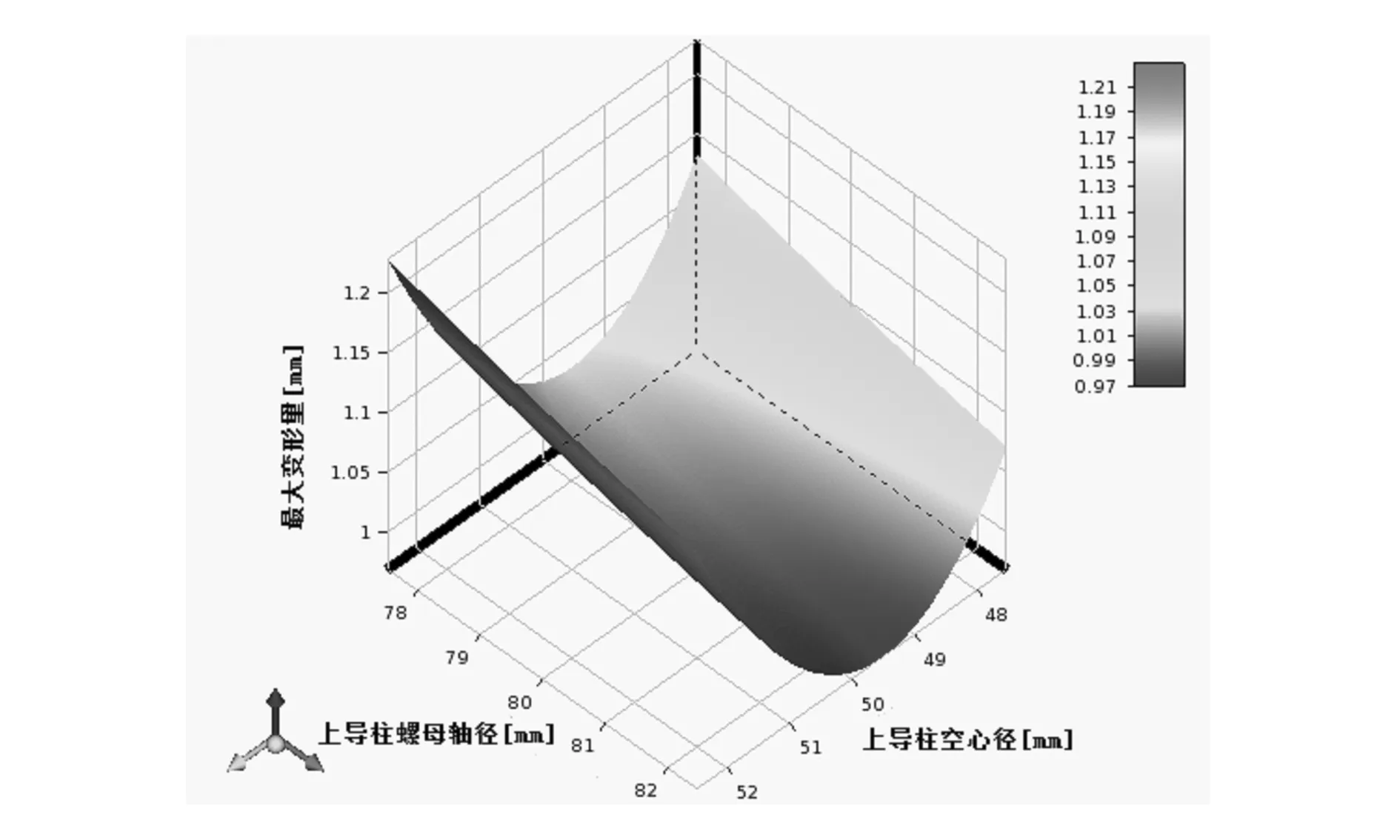
图9 变形响应面云图
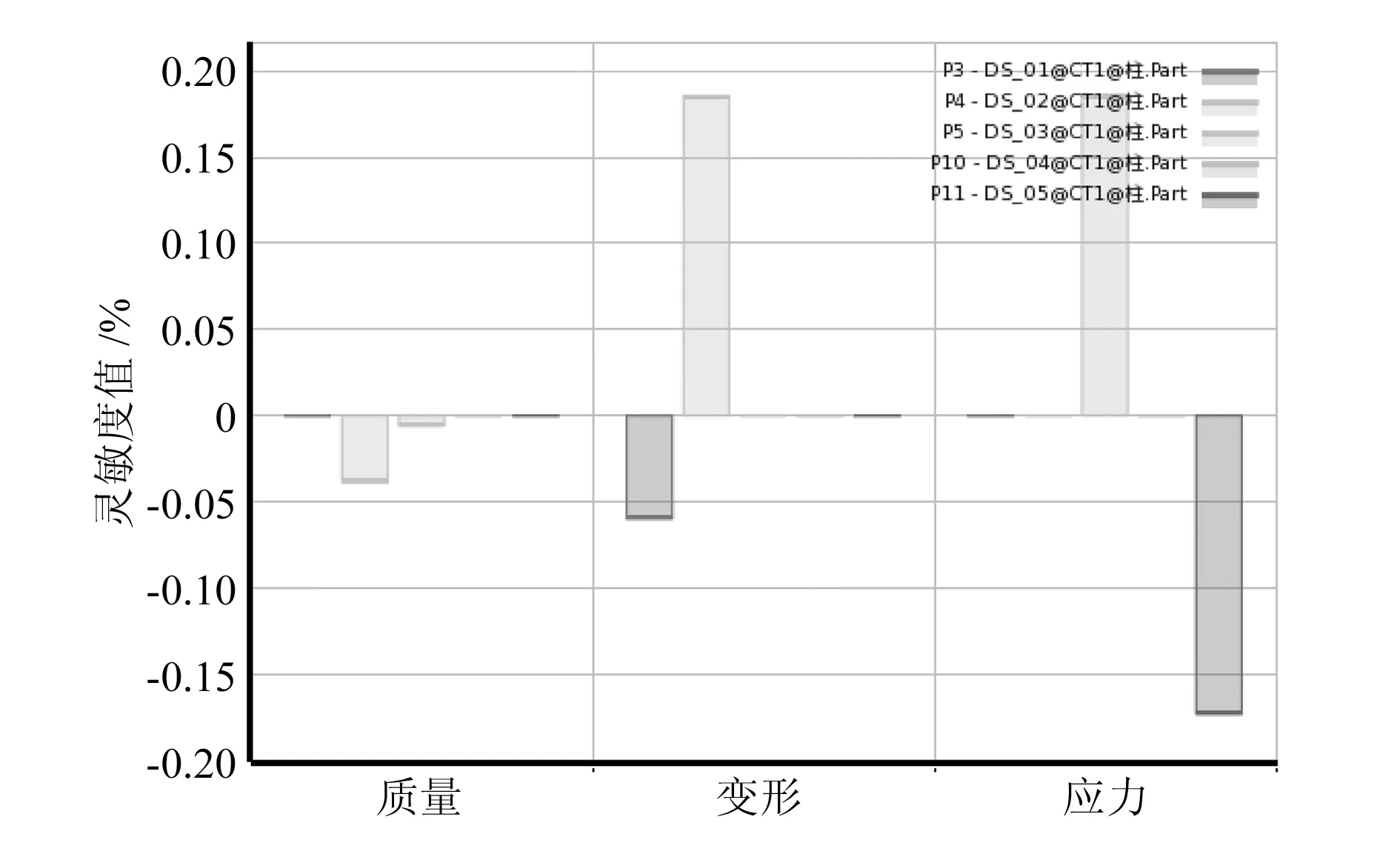
图8 设计变量对优化目标的灵敏度
图11为六西格玛设计后导柱部件的最大应力取值分布柱状图和累积分布函数。左侧纵坐标为概率密度,右侧纵坐标为可靠度。从图11的应力取值分布图可知,最大应力取值在65~75 MPa的概率最大,并且最大等效应力近似服从正态分布,证明模拟次数是充足的;从累积分布函数中得到的最大等效应力小于77.5 MPa的可靠度约为0.990 35。
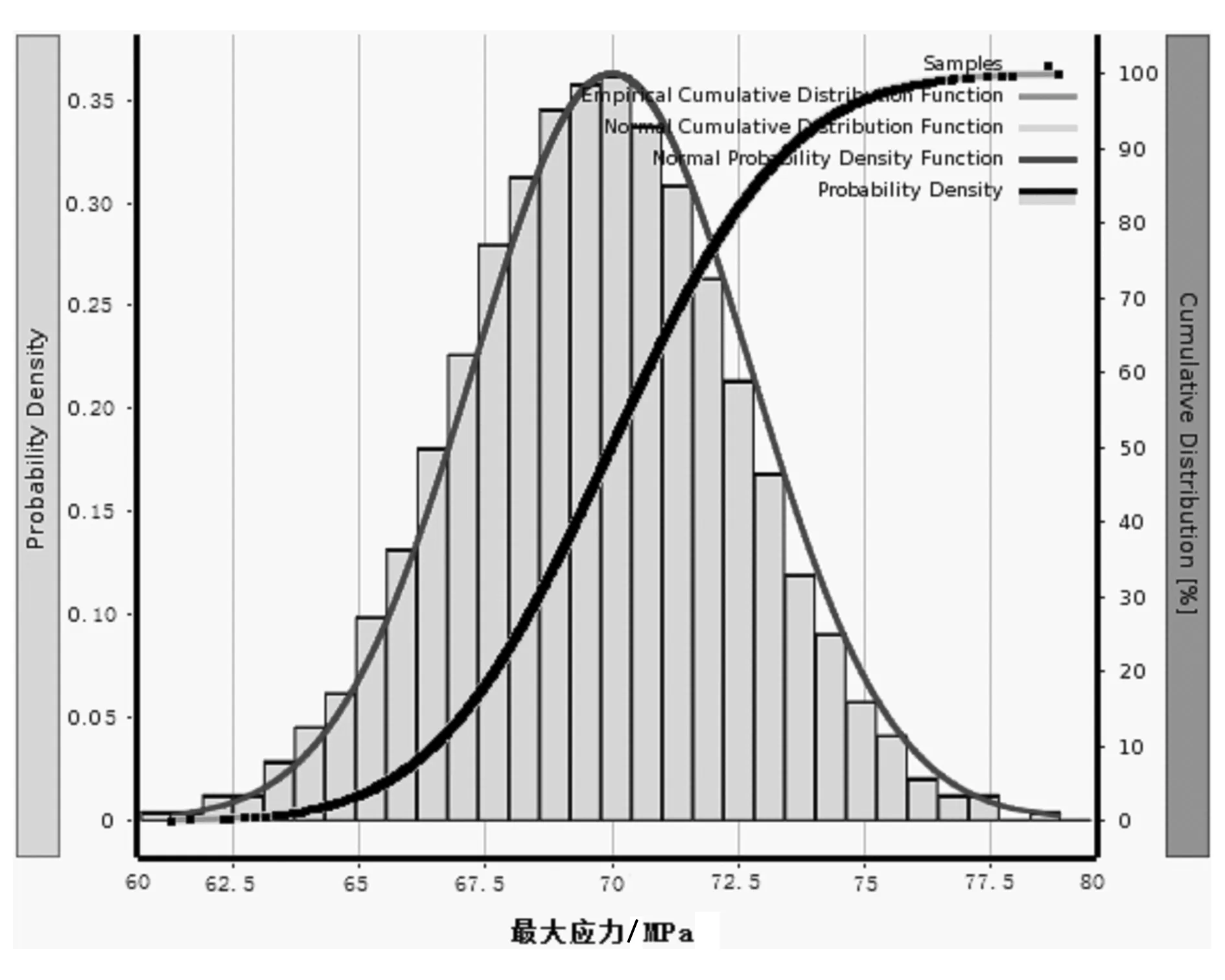
图11 最大应力柱状图与累积分布函数
通过对数据的分析和对比,可以得到最优的数据组合,优化参数取值见表1。将六西格玛优化后的导柱部件再次进行有限元模拟,计算结果见表2,改进后的导柱强度、刚度均满足要求。方案一在总变形δ减小14.81%、应力σ略减的情况下,质量m减轻了16.76%,提高了优化效率,实现了预期目标。

表2 导柱优化前后结果对比
4 结束语
本文对立式摩擦焊机导柱结构进行优化,能够明显改善它的受力状况、减小质量并让它的结构更加合理。优化结果表明,将拓扑与参数优化相结合的优化方法具有较高的优化效率,可为复杂机床导柱的优化设计提供一定的方向和指导。
