基于BWR状态方程的超临界二氧化碳主要热力参数推算

2021-06-15熊先闯刘正先李孝检

石油化工 2021年5期

熊先闯，刘正先，赵明，李孝检

（天津大学机械工程学院，天津 300350）

在压缩机的气动设计和流场模拟中，气体的热力参数计算是关键步骤之一，具体包括压力、温度、比体积（v）、焓、内能和熵等参数的计算。当压缩工质为实际气体时，如碳捕获与存储、超临界二氧化碳（SCO2）布雷顿动力循环中的压缩系统，由于存在实际气体效应，工质热力性质显著区别于理想气体[1]。如何快速准确地计算实际气体热力参数是开展以实际气体为工质的压缩系统热力设计及数值模拟的重要前提。SCO2是一种典型的实际气体。它具有较大的压缩系数、比热容和密度以及较小的黏性。在SCO2布雷顿循环中，流体工质较大的压缩系数使得压缩机消耗的功率较小[2-3]；又因工质高密度的性质，热力循环的几何结构变得更为紧凑，仅为蒸气循环的十分之一。此外，CO2的临界温度较低，相对于水等流体工质更容易达到临界状态。因此，以SCO2为工质的热力循环将有潜力取代传统水蒸气朗肯循环。实际气体热力参数计算的主要任务是依据基本热力参数（压力、温度、比体积或密度）推算出其他主要热力参数（内能、焓、熵等）及其衍生参数。描述基本热力参数之间函数关系的方程叫做状态方程。常见的状态方程有范德瓦尔方程、RK方程和PR方程等。不同状态方程适用的工质类型、温度、压力范围各不相同[4]。如RK方程对非极性或轻微极性气体pVT性质的计算结果符合较好，密度最大适用值可略大于临界密度，但如果含氢键，则会导致很大的误差。Span-Wagner（SW）模型是一种专门针对SCO2建立的以实验数据标定的半经验解析模型[5]。对于以SCO2为工质的热力系统，如果直接采用SW解析模型，那么计算过程将变得十分繁琐，众多的经验参数及高阶非线性特性使得它几乎无法直接推导出其他衍生热力参数的解析表达式。一种更普遍的计算方法是采用高阶样条曲线分段插值实验数据库以得到工质的物性参数表格[6-7]。NIST（美国国家标准与技术研究院）的REFPROP数据库，即为基于SW解析模型分段插值的物性表[8-10]。然而，调用REFPROP数据库生成宽范围、高精度的物性表，需要消耗较多的时间与内存。更重要的是分段插值方法难以得到基本热力参数精度较高的一阶或二阶偏导数信息，因而无法精确获得相关的衍生热力参数。Benedict-Webb-Rubin（BWR）状态方程[11]是精度最高的通用状态方程之一，它考虑了分子的聚集，能够较为准确地描述SCO2的基本热力参数。BWR方程具有物理意义明确、解析表达式简洁等优势。基于该状态方程及热力学普遍关系式（热力学第一定律、麦克斯韦关系式等）可推导出基本热力参数及其衍生参数快速准确的解析计算模型。解析计算模型对于实际气体热物理特性的研究具有重要理论意义，同时对于以SCO2为工质的热力过程设计与计算具有重要的工程应用价值。

本工作从热力基本关系式出发，结合BWR状态方程，采用了以标准状态为基准点，理想状态为中间过程的积分路径，推导了SCO2主要的热力参数快速计算解析表达式；并通过与REFPROP数据对比验证了解析模型在不同热力区的可靠性。

1 BWR状态方程及验证

状态方程的选择很重要，直接影响导出的物性模型精度，BWR方程能准确描述超临界流体的pVT行为，具体形式见式（1）。

式中，p为压强，105Pa；T为温度，K；v为比体积，cm3/kmol；R为通用气体常数，数值为8.314（cm3·MPa）/（kmol·K）-1；A0，B0，C0，a，b，c，α，γ均为经验参数。

在CO2温度范围300～600 K、压力范围7～30 MPa下，对应的经验参数值由文献[12]得到，见表1。

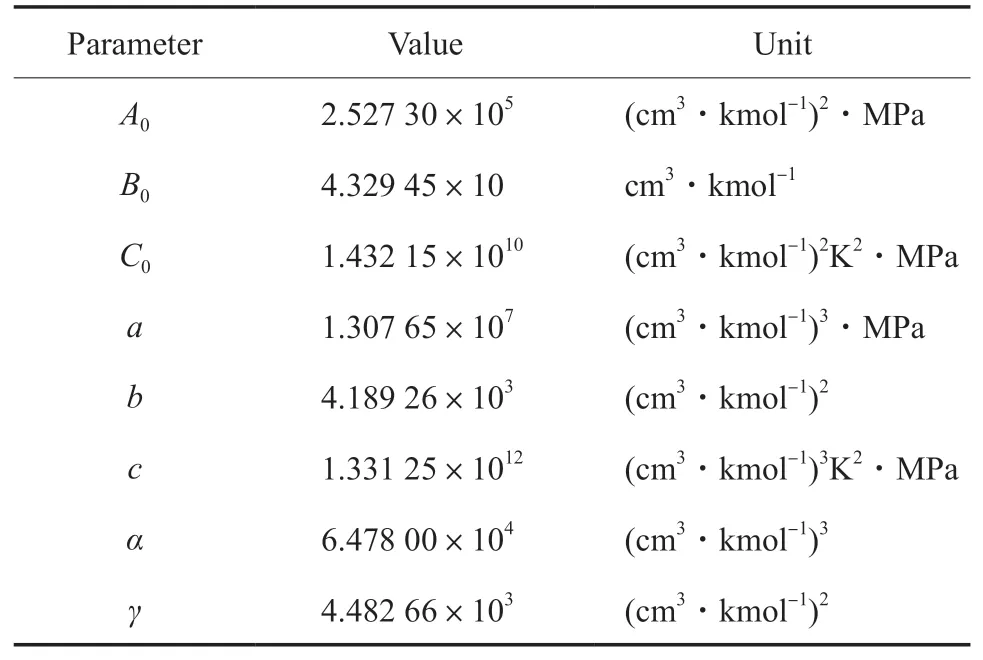
表1 BWR状态方程经验参数Table 1 Empirical parameter of BWR equation of state

为了验证拟合方程和参数质量的好坏，需要进行回代检验。在温度300～600 K、压力7～30 MPa内取样，通过REFPROP数据得到v，并进行相应的单位转换。将温度和v代入式（2），通过MATLAB编程计算，最后得到压力计算值（pcal）与REFPROP数据（pref）进行比较分析。pcal与pref在整个热力学区的相对误差在2.6%以内，平均相对误差仅为0.51%。参数质量及拟合方程对pVT行为描述较好，利用赋予这些参数值的BWR方程，进一步推算热力性质上是可靠的。本工作所有参考数据都是通过REFPROP软件查询得到的数据。压缩因子（Z）主要被定义为实际体积与理想体积之比，实际气体的状态方程引入了Z，简化形式见式（2）。结合式（1）与式（2），得到Z具体表达式（3）。

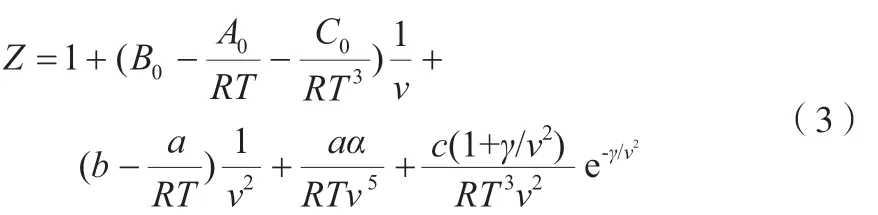
为了验证式（3）的精确性，将Z计算值与参考值进行比较。由BWR方程推算的Z最大误差不超过2.6%，全局平均误差0.52%，误差分布也比较平缓，无明显偏差点。

2 SCO2主要热力参数推算

2.1 基准点与积分路径

实际气体的热力性质为状态量，与过程无关。但是推导方法应用了热力普遍关系式，需要通过一定路径进行积分以及合适的基准点差值计算，才能保证结果的可靠性[13]。

以标准状态1（T1=298 K，p1=105Pa）为基准点，基准点热力学参数已知。积分路径常用的是从标准状态出发，先定压升温至待定状态温度T2，再定温升压至待定压力p2，但是由于积分量中涉及到比热项，是温度的函数，在不同压力下的表达式也不尽相同。为了避免被积函数的不定性，将比热函数设定为理想状态。先计算状态1等温膨胀到理想状态（p→0，v→∞），再对理想状态下的升温过程（T1→T2）进行计算，最后等温升压到待求状态2（T2，p2）。三个过程量叠加即为状态2与状态1的差值，状态1数据可由REFPROP直接查得。

2.2 内能

内能代表了储存于热力体系内部的能量，第一热力学能方程[14]见式（4）。

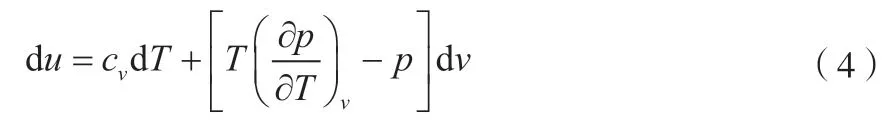
式中，u为内能，kJ/kg；cv为恒容摩尔比热容，kJ/（kg·K）。

对式（4）从状态1到状态2的路径进行积分，并计算得到差值，见式（5）。

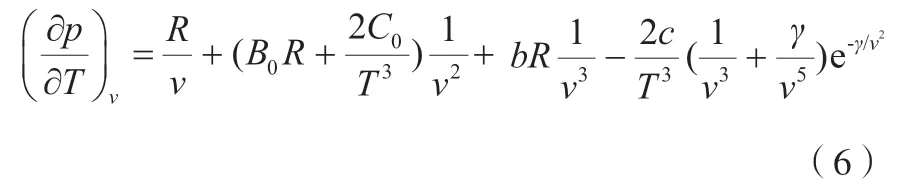
则式（5）中第一、三项中被积函数见式（7）。

第二项中被积函数为理想恒容摩尔比热容（cv∞）。理想恒压摩尔比热容（cp0）计算式见式（8）。

式中，参数通过实验数据拟合得到a0= 1.782×102，a1= 8.677×10-1，a2= -8.465×10-4，a3= 3.667×10-7。

由迈尔公式（9）得到cv∞。

被积函数已全部转换成T和v的具体表达式，代入式（5）积分求得内能差值，而u1为基准点内能（已知），即可得到待定状态2内能的快速计算式，经过换算最终单位为kJ/kg。

2.3 焓

焓是由开口系工质流动的特殊性而产生的一个新的状态参数，是热力系的热力学能与流动功之和。第二焓方程[14]见式（10）。

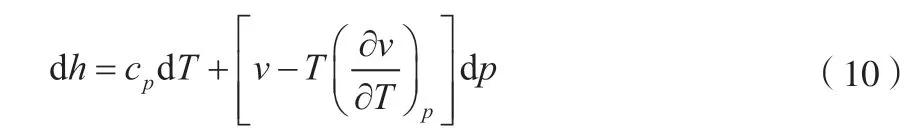
对式（10）沿指定路径积分，从状态1到状态2焓变见式（11）。

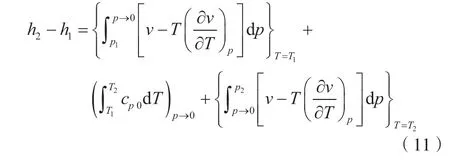
由于d（pv）=pdv+vdp，剩余项一般形式为式（13）。

将式（12）和式（13）合并即可得到式（10）中第一、三项的一般形式，见式（14）。

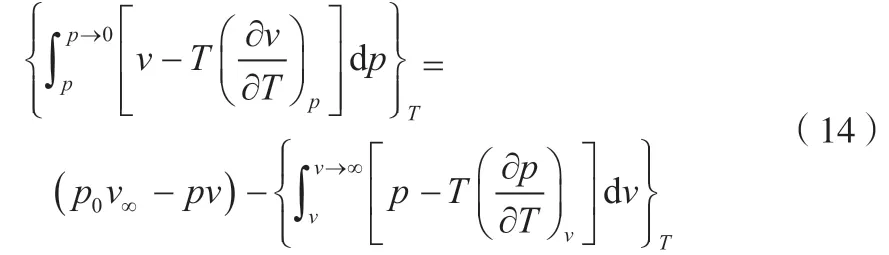
式（14）按照一般形式拓展即可得到可计算的焓差见式（15）。

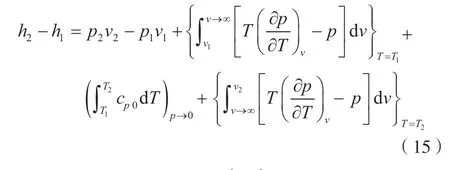
2.4 熵

熵的物理意义是体系混乱程度的度量，是构成体系的大量微观离子集体表现出来的性质。第一熵方程见式（16）。

沿指定路径积分，得到状态2与状态1之间的熵增，见式（17）。

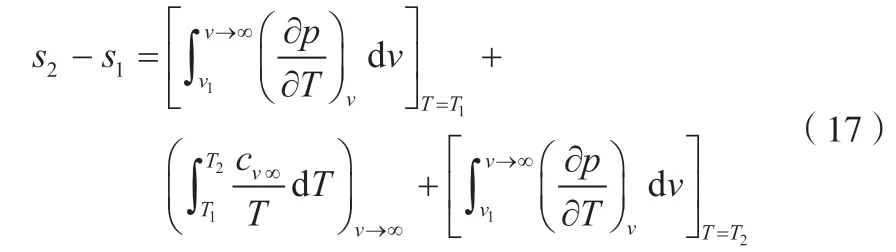
2.5 实际比热容

气体在压力和容积不变的条件下被加热时的比热容，分别为恒压摩尔比热容（cp）和cv。实际cv定义式为式（18）。

其中快速计算式已由式（5）得到，为T和v双变量解析式，经直接求偏导得式（19）。

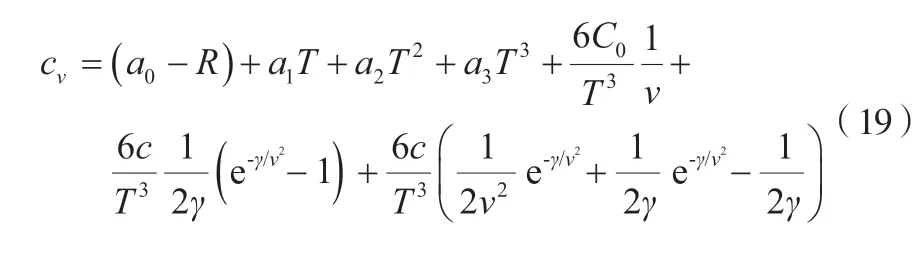
通过热容容差关系（不同下标关系、循环关系和麦克斯韦关系）整理可得式（20）。

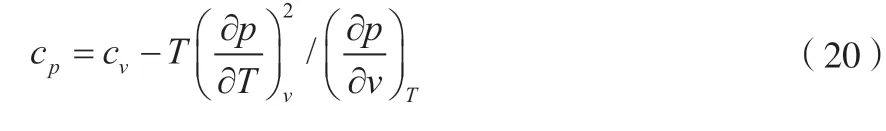
CO2的实际比热容已具化成T和v的快速计算式，输入变量即可与REFPROP数据对比精确性，换算后最终单位为kJ/（kg·K）。

3 结果与讨论

对上述推导得到的热力性质快速计算式，进行编程得到结果。为了分析计算结果在关键热力学区的可靠性，即温度T为300～600 K，压力p为7～30 MPa，比体积v大概在50～700 cm3/kmol之间。此区域横跨了临界点，包括了部分超临界区与部分亚临界区。取样绘图，由于此区域v跨度较大，而且v不随压力线性变化，采用常规方法采样无法突显CO2所处热力状态。故采用设置不同压力间接得到v的方法，得到对应的v，再将T和v代入快速计算式，得到对应的热力数据。绘制热力性质在不同温度下随v变化的关系曲线，并将计算值与REFPROP数据进行误差比较。

由于CO2在临界点附近物性的剧烈变化，提取温度300～320 K，压力7～8 MPa范围内数据，为近临界区结果比较分析。

3.1 内能

图1 为关键热力区及近临界区的内能计算值与参考值随v变化及误差分布。由图1可知，在关键热力学区，内能计算结果与REFPROP数据最大误差不超过2.7%，平均误差仅为0.65%；近临界点附近，最大误差不超过1.9%，平均误差0.61%。在相同v条件下，误差在320 K附近降至最低，在305 K附近会略微升高。在300～320 K区间，误差会随着v的升高而减小。在温度大于305 K的超临界区，误差基本稳定，温度及v的影响可以忽略，接近零。当v＞100 cm3/kmol时，误差降至低水平，且受温度影响变小。说明了内能计算结果的可靠性，对于采用CO2为工质的数值模拟与工程实践中，内能可采用本工作数据。而且在SCO2的应用中，结果具有更好地适用性。

3.2 焓

图2 为关键热力区及近临界区的焓计算值与参考值随v变化的误差分布。

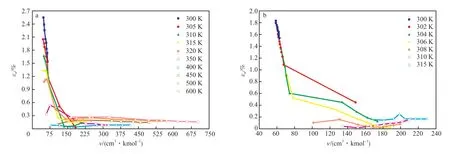
图1 关键热力区（a）和近临界区（b）内能相对误差Fig.1 Relative error of internal energy(εu) in key thermal area(a) and in near critical area(b).v：specific volume.

图2 关键热力区（a）和近临界区（b）焓相对误差Fig.2 Relative error of enthalpy(εh) in key thermal area(a) and in near critical area(b).

由图2可知，由于焓与内能的推导表达式类似，所以整体的数据分布差异不大，但也有一定区别。在关键热力学区，最大误差不超过2.5%，平均误差0.6%；近临界区最大误差不超过2.3%，平均误差0.58%。计算可知，焓的误差在可接受范围内，对于不同v区的精度分布与内能接近，即适用范围也相似。

3.3 熵

图3 为关键热力区及近临界区的熵计算值与参考值随v变化的误差分布。由图3可知，在关键热力学区，最大误差达到了15%，平均误差5.2%；在近临界区最大误差10%，平均误差5.3%。熵的计算误差较内能及焓普遍偏大，这与BWR方程本身以及推导方法有关。相同温度条件下，随着v的升高，误差逐渐减小，趋于稳定，最低能为1%。相反在v相同情况下，温度越高，误差也会随之增高。当v＞100 cm3/kmol时，误差降至低水平，变化平缓，且受温度影响不大。所以对于需要CO2熵的情况下，需要考虑工质的工作温度及v，以及项目对精度的要求。

3.4 实际比热容

对于实际比热容，推导过程中涉及到BWR方程的二阶偏导，精度相比其他热力性质会偏低，所以不对其近临界区做分析，但是给出计算数据与参考数据具体分布图可直观看出趋势。图4为关键热力区cp计算值及参考值和cp及cv的计算相对误差。由图4可知，在低温区（低于320 K）的差异较大，当v＞150 cm3/kmol时，比热容值变化较平缓，且计算误差也极小。但在305 K时，误差变化剧烈，所以当工况温度在305 K左右时，需要视精度要求使用。cv与cp平均误差分别为5.39%，3.28%。

图3 关键热力区（a）和近临界区（b）熵相对误差Fig.3 Relative error of entropy(εs) in key thermal area(a) and in near critical area(b).

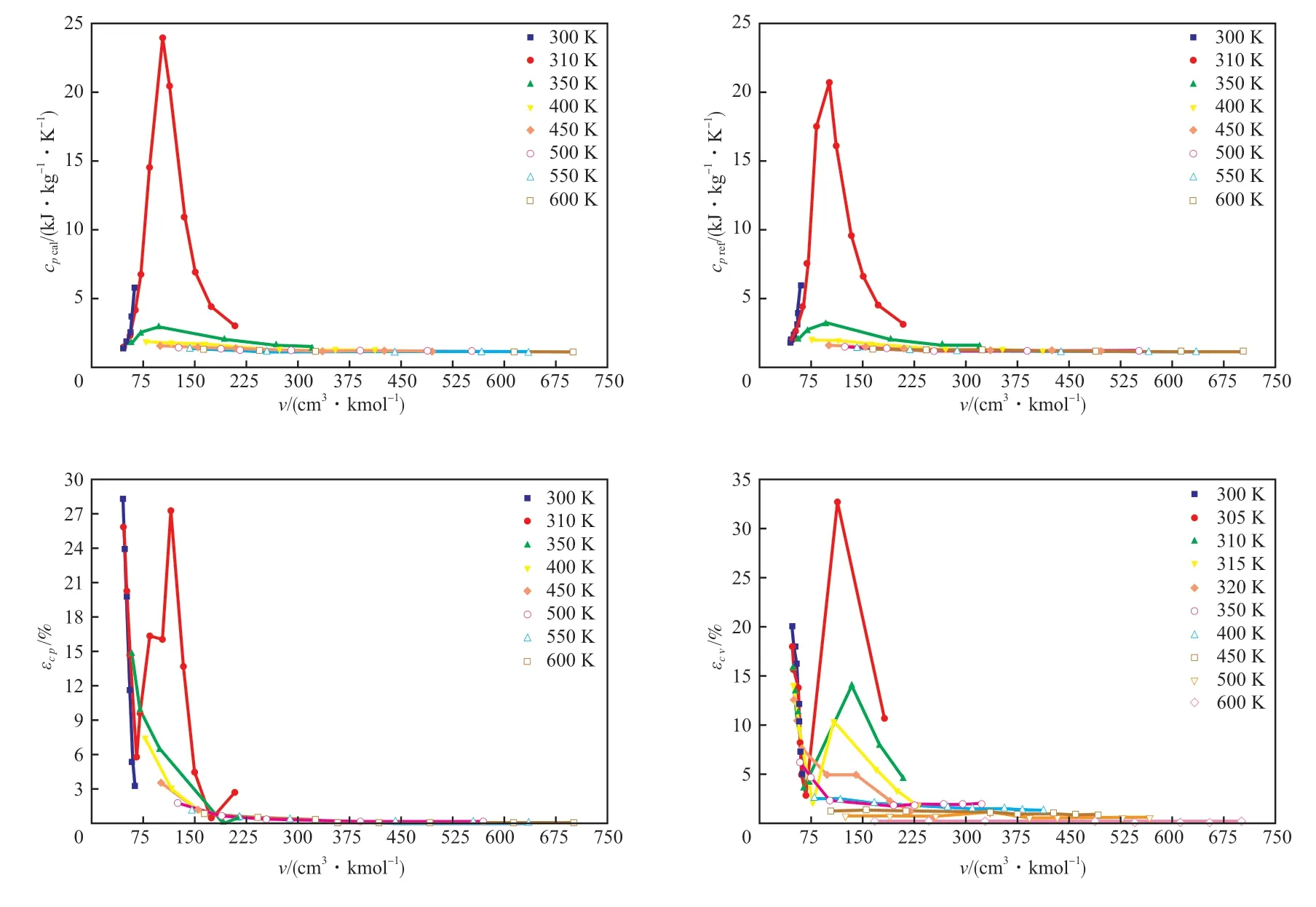
图4 关键热力区cp计算值及参考值（a-b）和cp及cv相对误差（c-d）Fig.4 Calculated and reference value of cp(a-b) and relative error of cp(c) and cv(d) in key thermal area.

对于上述热力性质，本工作的推导结果与REFPROP数据的误差在高于320 K的温度都比较小，整体的数据分布趋势符合度高。在临界温度附近（300～320 K），物性的变化趋势明显，虽然该区域的物性拟合难度较大，但结果还比较可观。热力性质快速解析计算模型在不同区域的平均误差见表2。

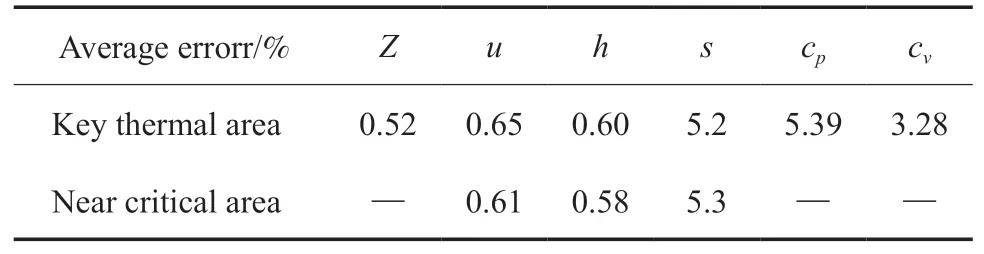
表2 快速解析计算模型平均误差Table 2 Average error of fast analytical calculation model

由表2可知，内能、焓、熵、cp及cv在关键热力区的平均误差分别为0.65%，0.60%，5.2%，5.39%，3.28%。

4 结论

1）对温度300～600 K、压力7～30 MPa范围内的CO2，首先进行方程参数质量验证。代入REFPROP数据，压力计算值与参考值在关键热力学区的平均误差仅为0.5%，参数质量以及拟合方程对pVT行为描述较好。对实际气体引入Z，Z的计算结果与REFPROP数据符合良好，平均误差

0.52%。

2）推算了热力性质的快速计算定量表达式，包括内能、焓、熵、比热容。对结果进行了全局比较以及近临界区的加密取样比较，平均误差都在可接受范围以内。内能、焓、熵、cp及cv在关键热力区的平均误差分别为0.65%，0.60%，5.2%，5.39%，3.28%。对于v＞100 cm3/kmol状态，尤其是温度高于320 K的SCO2，本工作计算结果均与REFPROP数据接近，可适用于高精度计算要求。

符号说明

A0，B0，C0，a，a0，a1，a2，a3，b，c，α，γ经验参数

cp恒压摩尔比热容，kJ/(kg·K)

cp0理想恒压摩尔比热容，kJ/(kg·K)

cv恒容摩尔比热容，kJ/(kg·K)

cv∞理想恒容摩尔比热容，kJ/(kg·K)

h焓，kJ/kg

p压力，Pa

R通用气体常数，8.314 (cm3·MPa)/(kmol·K)-1

s熵，kJ/(kg·K)

T温度，K

u内能，kJ/kg