基于ABAQUS的牙轮钻头镶装工艺

2021-06-11吴泽兵周珂飞赵海超郑维新张文超

西安石油大学学报（自然科学版） 2021年3期

吴泽兵，周珂飞，赵海超，黄海，郑维新，张文超

(西安石油大学机械工程学院，陕西西安710065)

引言

牙轮钻头是使用在石油钻井工业中有效的破岩工具之一，主要以变角度的压入加刮凿破碎岩石，牙齿在破岩过程中作三维复合运动[1- 2]。由于钻头工作环境复杂，工作时承受钻压、弯矩和剪切力等反复作用，牙齿失效现象[3-5]时有发生。长期以来，学者和研究人员针对牙轮钻头作了一定研究，从目前研究来看，主要针对钻头设计以及压齿力、固齿力计算等方面[6-8]。陈涵宇等[9]通过分析传统的布齿结构提出了一种新型倒锥齿结构，可以有效提高牙齿的固紧力，减少了脱齿现象的发生；邓嵘等[10]采用拉宾诺维奇磨粒磨损模型，建立牙齿与岩石互作用模型，探索了转速、钻速与牙齿磨损之间的关系；谢苗等[11]根据牙轮钻机钻井时钻头纵向振动特性对牙轮轴端的影响进行牙轮轴端磨损机理分析，对提高牙轮钻头寿命具有一定的积极作用。但总体来说，对钻头牙齿失效研究较少，特别是镶齿牙轮钻头牙齿镶装工艺方面的研究较少。

在实际钻井中，钻机施加足够大的轴压作用在牙轮钻头上，将镶嵌在牙轮上的合金齿嵌入岩土表层，同时主机钻杆带动牙轮钻头作旋转运动进行破岩，载荷主要通过牙齿传入岩石，容易出现牙齿脱落、磨损等[12-13]现象，造成部分钻头因牙齿失效而报废，牙齿脱落是钻头失效的一种重要形式。研究表明，牙齿脱落主要是由于牙轮对牙齿缺乏足够的固齿力，为了降低钻井成本，提高钻井效率，减少钻头失效[14-16]问题的发生，目前，针对钻头牙齿失效问题，主要从设计、加工、装配工艺和使用等方面进行改进。本文利用有限元分析软件，研究不同镶装工艺对镶齿牙轮钻头固齿力、Mises应力、变形等[17-21]的影响规律，通过模拟不同工艺得到固齿力、压齿力等参数，总结了不同镶装工艺对镶齿牙轮钻头的影响，通过对比不同镶装工艺对钻头的影响确定最佳镶装工艺，对钻头实际生产加工具有一定参考意义。

1 牙轮钻头镶齿数值模拟方法

本文基于有限元分析软件ABAQUS模拟计算不同镶装工艺所产生的应力-应变场。其中，建立准确的牙轮钻头牙齿镶装有限元模型是进行牙轮钻头牙齿镶装的关键。首先，为了提高计算效率，对单牙轮钻头模型进行合理简化，采用简化单齿孔模型来研究牙齿镶装；其次，在ABAQUS软件中定义材料属性，依据实体模型划分网格，建立温度-位移耦合分析步，选择合适的单元类型，根据实际加工设置边界条件，求解其应力-应变场。

1.1 有限元模型

由于ABAQUS软件实体建模的局限性，首先在Creo中建立三维几何模型，然后以x_t格式导入ABAQUS进行分析计算，81/2″(215.9 mm)牙轮钻头全齿模型如图1所示。在有限元模拟时考虑计算速度与精度，采用简化单齿孔模型，并利用ABAQUS软件进行几何模型的网格划分，其几何尺寸与网格划分如图2所示。牙齿齿根倒角60°，直径14 mm，齿孔深度13 mm，齿孔外径32 mm，齿孔内径13.94 mm，即牙齿和齿孔间的配合过盈量为0.06 mm。由弹性力学理论圣维南原理可知，模型简化后对分析精确度的影响非常小，分析结果在精度要求范围内，同时去除离齿孔区域不远处的牙轮壳体可以节省大量分析时间。

图1 牙轮钻头模型Fig.1 Model of roller cone bit

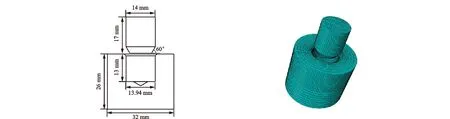
图2 简化单齿孔模型与网格划分Fig.2 Simplified single tooth hole model and meshing

为了提高计算效率，采用单精度网格的划分方式，划分完成后共有57 726个节点，51 178个网格单元。采用热-弹塑性有限元法来分析牙轮钻头单齿孔镶装的残余应力、压齿力与变形，由于温度场作用方式简单，因此以完全耦合的方式进行计算，即在计算时先设置温度-位移耦合分析步，修改网格单元属性为温度-位移耦合，并考虑热装后的散热问题，设置接触面、表面热交换条件、表面辐射。

1.2 材料参数

根据牙轮钻头的工作情况和受力特点，牙轮壳体材料选用具有高淬透性、高强度、表面硬化加工的渗碳钢20Ni4Mo，强度极限1 423 MPa。以往部分镶齿牙轮钻头研究中，为了简化分析，将牙齿视为刚体，本文依据实际情况，牙齿采用高强度、高冲击韧性、弹塑性较好的钨钴类硬质合金YG06A，抗弯强度3 200 MPa，其热物理性能参数与文献[22]相同。牙齿与齿孔力学性能参数见表1。

表1 牙齿与齿孔材料参数Tab.1 Material parameters of tooth and hole body

1.3 镶装工艺的确定

镶齿牙轮钻头目前没有明确的镶齿工艺，在加工牙轮时首先钻齿孔，然后工人通过压力机将牙齿逐个压入齿孔，压齿后牙轮有轻微变形，通过精车牙轮内孔的方式保证精度。常规过盈配合装配工艺主要有热装、冷装及常温镶装。以钻头镶齿为例，热装是指在镶齿前将齿孔加热到一定温度，然后进行镶齿；冷装是指在镶装前利用干冰或液氮将牙齿冷却到一定温度，再进行镶装；常温镶装即在室温条件下将牙齿压入齿孔。目前，针对镶齿牙轮钻头，因牙齿材料碳化钨性质硬而脆，牙轮材料为热适应性较好的合金结构钢，故在实际生产加工中主要以常温镶装和热装为主，采用加热牙轮壳体后装入碳化钨牙齿，待齿孔冷却后抱紧牙齿的方法完成过盈装配。本文主要研究20 ℃、100 ℃、200 ℃、300 ℃和400 ℃的镶装温度对牙齿、牙轮齿面性能影响的规律。

2 镶装结构理论分析及有限元模型验证

过盈配合时，当牙齿与齿孔过盈量增大到一定值时齿孔势必出现塑性变形，而塑性力学理论知识求解塑性变形的解析解很困难。本文所运用ABAQUS有限元分析方法是否准确可行需要验证，但在塑性变形阶段很难验证；在牙轮材料弹性范围内求解其弹性理论解，将有限元分析结果与理论解进行对比验证有限元方法的可行性。

2.1 理论分析

为了便于分析，将牙轮与牙齿的装配体简化为厚壁圆筒与实心圆柱的模型。对该单齿孔模型用弹性力学解析，如图3所示。

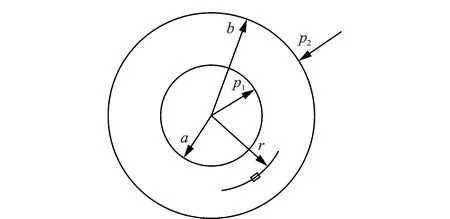
图3 理论模型Fig.3 Theoretical model

(1)孔的受力分析

根据拉梅公式，则有

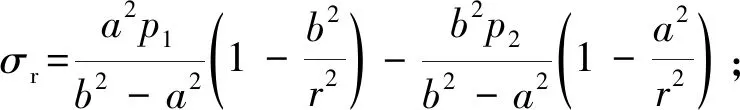
(1)

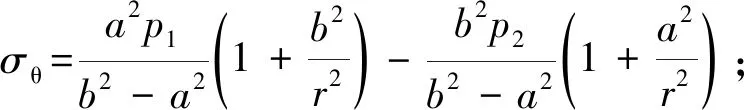
(2)

(3)

式中：p1、p2分别为厚壁圆筒的内压、外压，Pa；σθ为内、外压共同作用下的周向应力，Pa；σr为径向应力，Pa；u为径向位移，m；μ为泊松比；E为弹性模量，GPa；a为齿半径，m；b为孔半径，m；r为齿孔壁厚半

径，m。

该单齿孔模型不考虑相邻齿孔的应力交互影响，孔壁仅受内压作用，根据圣维南原理，外压p2=0，孔半径b→∞，由式(1)—(3)得

(4)

(5)

(6)

式中：μk为牙轮材料泊松比；Ek为牙轮材料弹性模量，GPa。

(2)齿的受力分析

牙齿简化为实心圆柱，牙齿与齿孔接触面只受到均布载荷作用，p1=0，齿半径a→0，径向位移可用

(7)

表示。式中：μc为牙齿材料泊松比；Ec为牙齿材料弹性模量，GPa。

(3)牙齿与齿孔过盈配合受力分析

由于牙齿与齿孔有过盈配合，实际齿孔半径比牙齿半径小，则在过盈配合后牙齿和齿孔之间会产生径向压力p。设过盈量为δ，则完成过盈配合装配

后牙齿外壁半径的减量与齿孔壁半径的增量之和必须为δ，由式(6)、(7)得

(8)

则得

(9)

式中：δ为半径过盈量，m；p为径向压力，Pa。最终得到牙齿与齿壁的径向压力p作为固齿力，即牙齿表面与齿孔表面法向接触力。

轴向应力与周向应力、径向应力相比很小近似为0，其中这3个应力均为主应力，依据屈服准则下的Mises应力求解公式得

(10)

式中：σz为轴向应力，Pa。

2.2 模型验证

对于本文镶装方法的可靠性，采用理论计算与模型仿真进行对比，验证模型如图4(a)所示。为了在弹性范围内求其理论解，该理论计算模型齿孔过盈量为0.02 mm，镶齿完成后固齿力云图如图4(b)所示，固齿力峰值为383.3 MPa。

图4 理论计算模型及固齿力云图Fig.4 Theoretical calculation model and tooth fixing force nephogram

由式(8)可以计算出过盈量为0.02 mm时径向压力为190.1 MPa，由式(9)计算得Mises应力为337.8 MPa，理论计算得到的是齿孔壁所受应力平均值，对ABAQUS计算结果的固齿力和Mises应力分别求平均值，即选取沿齿孔壁深度方向任意一条路径，并对该路径固齿力与Mises应力分别求平均值，理论计算对比见表2。由表2可知，固齿力和Mises应力的误差分别为11.31%、7.22%，在工程误差范围内，表明本文有限元方法正确，保证了数值计算的准确性和可靠性。

3 仿真结果分析

根据实际起出钻头来看，固齿失效主要有：齿孔壁产生严重塑性变形，牙轮表面磨损严重导致牙齿露出高度增加，埋深减少，固齿强度显著降低等。由此可见，为防止掉齿，首先保证钻头不会因屈服而产生孔壁塑性变形，其次保证齿孔给予牙齿更大的固紧力。因此在分析时着重考虑最大固齿力与塑性变形。

通过仿真计算，在0.06 mm过盈量下，不同镶装温度下Mises应力云图分布趋势基本一致，以常温20 ℃镶装为例，牙齿与齿孔Mises应力分布如图5(a)所示，应力峰值出现在牙齿上为1 176 MPa，牙齿材料屈服强度为1 150 MPa，Mises应力超过屈服强度但未超过强度极限。齿孔对牙齿的固齿力，即齿孔与牙齿表面接触时的法向压力，如图5(b)所示，牙齿和齿孔固齿力分布趋势一致，并且在牙齿齿根与齿孔底部固齿力达到最大值，分别为1 209 MPa和953 MPa，未超过齿孔屈服强度1 035 MPa，也没有超过牙齿材料强度极限，保证了牙齿与齿孔正常工作不被破坏。

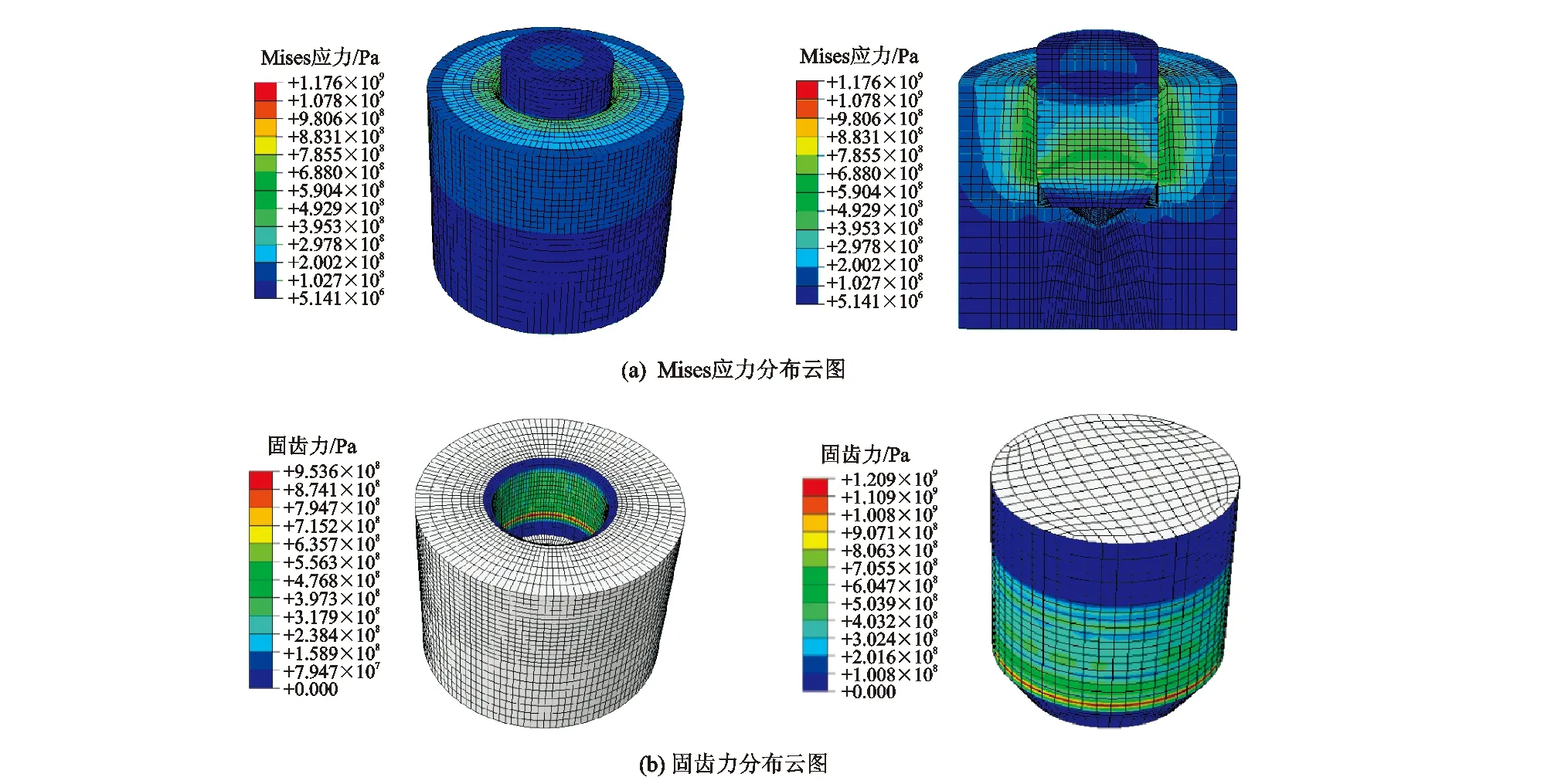
图5 Mises应力与固齿力分布云图Fig.5 Mises stress and tooth fixing force nephograms

图6(a)为沿齿孔壁的Mises应力曲线图，可见随着齿孔深度的增加，Mises应力逐渐减小，但在齿底Mises应力有所增加。不同镶装温度下，在沿齿孔深度方向上应力变化趋势一致，过盈量0.06 mm时牙轮材料处于弹塑性共存的状态，牙齿与牙轮的接触不连续不充分，但随着镶装温度的升高，Mises应力沿齿深度方向波动减少，且应力峰值降低，20 ℃时Mises应力峰值为861 MPa，400 ℃时Mises应力峰值为706 MPa，峰值应力减少了18%，减小了镶装对齿孔的冲击破坏作用。图6(b)为Mises应力均值柱状图，可见随着镶装温度的升高，Mises应力急剧增加，在200 ℃后趋于稳定。

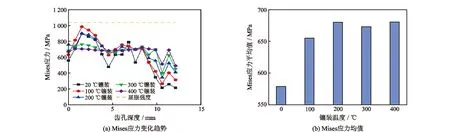
图6 不同镶装温度下齿孔壁Mises应力分布Fig.6 Mises stress distribution

沿齿孔深度固齿力曲线如图7所示。从图7(a)可以看出，在沿齿孔深度方向，固齿力逐渐增大，在齿孔有效接触深度7.5 mm处固齿力陡增，8.5 mm处达到峰值，随后逐渐下降，最后变为0，这是由于牙齿根部存在倒角，因此在牙齿镶装完成后，在齿孔底部无接触，因此不存在固齿力。分析不同温度的镶装结果(图7(b))可以看出，随着镶装温度的升高，固齿力逐渐升高，在200 ℃以上增幅逐渐减小，由于高温镶装时齿孔逐渐出现塑性变形，接触压力增幅减缓。考虑材料的屈服强度，在300 ℃、400 ℃镶装时，固齿力达到峰值1 253 MPa，远远超过牙轮壳体材料屈服强度1 035 MPa，但未超过材料强度极限，200 ℃镶装略微超过屈服强度，为保证镶装后残余应力较为平缓，可以考虑采用200 ℃镶装工艺。

图7 不同镶装温度下沿齿孔深度固齿力分布Fig.7 Tooth fixing force distribution in tooth hole depth direction

图8为不同镶装温度下的压齿力曲线，压齿力即压力机将牙齿压入齿孔所需的压力大小。从图8(a)中可以看出，不同镶装温度下压齿力变化趋势一致，在初始时无变化，原因是牙齿还未与齿孔接触，随着镶装的进行，牙齿开始缓慢压入齿孔，压齿力随着压入深度的增加而增加。但在不同镶装温度下压齿力峰值有所不同，即在实际镶装时所需最低压齿力不同，如图8(b)所示，随着镶装温度的升高，齿孔膨胀，减少了过盈配合量，所需压齿力逐渐降低，在400 ℃时压齿力峰值最小，所需最低压齿力较小，相比常温镶装压齿力降低了5.2 kN，有利于牙齿镶装顺利进行，对镶齿设备要求较低，便于加工。

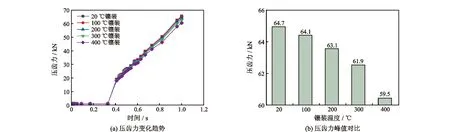
图8 不同镶装温度下的压齿力Fig.8 Tooth inserting force at different temperatures

齿孔变形曲线如图9所示。由图9(a)可知，不同镶装温度对齿孔壁径向位移变化趋势的影响基本一致，在初始镶装时，齿孔处变形骤增，随之波动后达到稳定，在冷却时由于材料收缩，径向变形稍有减少并达到稳定值，但不同镶装条件对齿孔变形值影响较小。沿齿孔深度方向齿孔壁的径向位移如图9(b)所示。由图9(b)可知，镶装温度对沿齿孔深度齿孔壁径向位移趋势的影响一致，随着镶装温度的升高，齿孔径向位移逐渐增大，在齿孔壁上部，变形较为平缓，在8.5 mm处不同镶装温度变形相同，随后开始下降，在高温镶装时，齿孔下部径向变形更大，并且变形方向相反，这是由于在0.06 mm过盈量下，存在牙齿切削齿孔内壁的情况，压齿结束后，塑性变形被更多地“推到”底部，温度越高影响越明显，随后冷却时由于热胀冷缩效应，在齿孔下部出现了反向变形且高温镶装时影响更为明显。