基于Cross本构方程的裂缝内清洁压裂液支撑剂铺置行为数值模拟

王治国，蔺靖杰，郭姜汝，孙 晓，苏晓辉，张 恒

(1.西安石油大学 机械工程学院，陕西 西安710065； 2.陕西延长石油(集团)有限责任公司 研究院，陕西 西安 710065)

引 言

水力压裂是油气藏增产的一项重要技术手段[1]，其目的是在地层内形成一条高导流能力的裂缝[2]。支撑剂在裂缝中运移与沉降所形成的砂堤形态直接决定着压裂后的油气产能[3]。压裂液的流变特性对裂缝内支撑剂的铺置行为具有重要影响。目前油田用到的压裂液有滑溜水、胍胶、泡沫压裂液以及清洁压裂液[4-7]。清洁压裂液是由低分子量的黏弹性表面活性剂在反离子作用下形成三维缠绕的蠕虫网状胶束[8]，这种压裂液呈现典型的非牛顿流体特征，其携砂能力不仅取决于黏度，而且与其内部形成的微观网状结构有关[9]，同时，压裂液破胶后黏度迅速降低，可以利用地层压力返排出地面，不产生任何残渣，对地层伤害小，近年来在油气田压裂中逐渐得到较为广泛的应用[3]。

针对支撑剂在裂缝中的运移与展布问题，国内外进行了大量的室内实验[10]和数值模拟研究[11]，初步明确了裂缝形态、支撑剂参数、压裂液性能等对支撑剂在裂缝内的运移与展布会造成影响。Kern和Perkins[12]采用了“砂堤平衡高度”的概念描述了颗粒沉降状态与压裂液运动速度之间的关系。但是以上实验和模拟中，较少考虑压裂液的非牛顿流变参数对砂堤铺置规律的影响。本文采用非牛顿Cross本构方程，结合颗粒动力学理论，对支撑剂在黏弹性表面活性剂形成的清洁压裂液中的运移过程进行数值模拟，拟研究压裂液流变性质对砂堤平衡高度的影响规律，为清洁压裂液中支撑剂运移施工设计提供参考。

1 CFD数值模拟

1.1 控制方程

液相与固相的连续性方程分别为：

(1)

液相和固相的动量方程分别为：

(2)

其中：SD=-MD+Fs。

(3)

式中：下标i表示相，i=l表示液相，i=s表示固相；α为体积分数，%；ρ为密度，kg/m3；u为速度，m/s；τ为层流应力，Pa；τ′为湍流应力，Pa；动量源SD由固体颗粒间的碰撞力和相间动量传递项组成，MD为相间动量交换系数，Fs为固相颗粒之间的碰撞力；p为压力，Pa。

动量交换系数MD表示流体相和颗粒相间总的作用力，其包括流体相与颗粒相间曳力(FD)、颗粒所受虚拟质量力(FVM)，以及颗粒升力(FL)，表示如下：

MD=FD+FVM+FL。

(4)

其中：

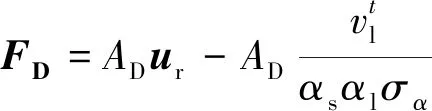
FL=CLαsρsρlur×(∇×ur)，

1.2 湍流模型

湍流模型采用标准k-ε湍流模型，其中湍动能方程为：

(5)

湍流扩散率方程：

(6)

式中：Gk，Gb分别为有层流速度梯度和浮力产生的湍流动能；σk，σε分别为k方程和ε方程的湍流普朗克数；C1ε，C2ε，C3ε为常数；YM为扩散产生的波动；Sk，Sε为自定义函数。

1.3 颗粒动力学理论

固体颗粒加入后会引起混合物黏性增加，颗粒动力学理论引入Eular-granular 黏性来处理这一问题。Eular-granular黏性ηg由颗粒碰撞附加黏性ηg,col、颗粒湍动附加黏性ηg,kin以及颗粒之间的摩擦产生的附加黏性ηg,fr3部分组成：

ηg=ηg,col+ηg,kin+ηg,fr。

(7)

其中，由于颗粒碰撞引起的附加黏性

(8)

而由于颗粒湍动引起的附加黏性

(9)

式中，Θs为granular温度，其计算过程需要求解关于Θs的输运方程，方程的张量形式为：

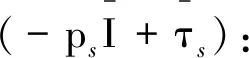
(10)

方程(10)左边第一项为由于固相应力张量所产生的能量，实际求解过程中忽略方程的对流和扩散项，采用代数方程求解。第二项为由于固相(s)之间的颗粒碰撞所消耗的能量，其求解公式参考Lun等[13]的研究成果：

(11)

第三项为由于颗粒速度的随机波动引起的固相和液相以及固相之间的湍动能传递项：

φls=-3KlsΘs。

(12)

式中，Kls为系数。

本文采用的Eular-granular模型基于以下假设：将支撑剂颗粒看作连续相，与流体相之间相互贯通，且满足动量和质量守恒；携砂非牛顿流体在平板裂缝中为瞬态流动；支撑剂的粒径视为等直径；忽略颗粒的旋转运动。此模型计算量大，精度高，适用于流动中有相混合或者分离，或分散相体积分数较大的情况。在Fluent软件中，模拟固液两相流的设置见表1。

表1 固液两相流模拟参数设置[14]Tab.1 Simulation parameters of solid-liquid two-phase flow

1.4 清洁压裂液的流变性

选用质量分数1.4%的十八烷基三甲基氯化铵(OTAC)与0.35%的水杨酸钠(NaSal)形成的黏弹性表面活性剂清洁压裂液为实验药品[15]，采用德国HAKKE公司的RS300控制应力旋转流变仪研究清洁压裂液的剪切流变性。该流变仪配备了旋转圆筒与锥板等测试单元，其中旋转圆筒用来测量稳态剪切流变。其外筒半径为7.965 mm，内筒半径为6.665 mm，间隙宽度为1.3 mm，圆筒的高度为40 mm，每次可以测量的样品体积为50 mL。测试时，将样品倒入两筒的间隙，旋转圆筒以不同速率旋转，流体在环形空间内做层流运动，通过测量内筒旋转所需要施加的扭矩得到流体的应力和剪切速率之间的关系。

采用Cross流体本构方程对剪切流变实验数据进行拟合：

(13)

式中：η0为零剪切黏度，Pa·s；λ为表征清洁压裂液结构稳定性的松弛时间，s。

拟合结果如图1所示。拟合参数：η0=2.661 Pa·s，λ=0.629 s，n=-0.43，拟合度R2=0.99。

由图1可知，Cross本构方程与清洁压裂液的流变测试实验数据吻合较好，能够描述清洁压裂液在低剪切速率时的零剪切黏度，同时可以较为准确地描述其结构稳定性。Cross本构方程中的流变指数n可以描述非牛顿流体的剪切稀释性，Cross模型还考虑了清洁压裂液在低剪切速率时的零剪切黏度η0，而η0对非牛顿压裂液的支撑剂运移具有重要影响[16]。此外，清洁压裂液的微观结构稳定性也是体现支撑剂运移能力的一项重要指标[17]，而Cross本构方程中的结构松弛时间λ则能够在一定程度上反映清洁压裂液的微观结构稳定性。

图1 清洁压裂液流变曲线及Cross本构方程拟合Fig.1 Rheology experiment data of clean fracturing fluid and their Cross constitutive equation fitting

1.5 几何建模与网格划分

采用瞬态CFD模拟方法，基于Cross本构方程对支撑剂在裂缝内运移过程进行数值模拟。所取地层裂缝模型为长L=100 cm，高H=20 cm，宽W=1 cm的裂缝，左右两侧各有2个直径φ=0.8 cm的进出孔，两圆孔之间的距离D=5 cm，底端孔距离长方体裂缝底部的距离M=8 cm。此裂缝模型的形状规则，整个计算区域均采用正六面体结构化网格，模型建立及网格划分采用ICEM前处理软件，划分结果如图2所示。

图2 模型及网格划分示意图Fig.2 Crack model and its mesh generation

对三维计算区域的网格进行处理得到3种疏密程度不同的网格，M1网格数量为18 200，M2为34 000，M3为71 928。基于上述3种计算网格，对其进行网格的无关性验证。流体介质为清水，支撑剂密度为1 800 kg/m3，粒径为0.6 mm，携砂液入口速度为1 m/s。对比网格的疏密程度对支撑剂在裂缝中分布的影响，模拟600 s时支撑剂在裂缝中的分布情况，如图3所示，不同网格间的计算结果差异仅为计算节点的疏密，差距非常小。考虑到模拟的经济性，选取M2网格完成所有模拟计算。

图3 网格无关性验证Fig.3 Validation of grid independence

2 数值模拟结果分析

2.1 数值模拟可靠性验证

通过与前人[18]的实验结果进行对比，验证本次模拟方法的准确性。如图4所示，实验采用长300 cm，高50 cm，宽2 cm的长方体可视化裂缝，左右各有1个进出口，实验时所用压裂液为清水，黏度为0.001Pa·s，支撑剂采用粒径为30/50目(平均粒径0.45 mm)，密度为2 770 kg/m3的陶粒，砂比为3%，流量为4 m3/h，换算速度为3.704 m/s。

图4 模型示意图Fig.4 Model diagram

压裂液体积为0.8 m3，支撑剂质量为34.8 kg，90 s、476 s以及710 s时支撑剂在裂缝内分布的实验结果如图5所示。

图5 实验结果Fig.5 Experimental results

90 s、476 s以及710 s时支撑剂在裂缝内分布的数值模拟结果如图6所示。

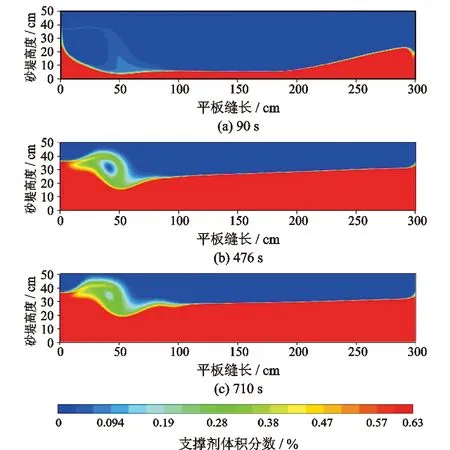
图6 数值模拟结果Fig.6 Numerical simulation results

图6中，红色区域为砂堤区，支撑剂在裂缝中稳定沉降形成砂堤，黄色区域为颗粒滚流区，此时支撑剂沉降与卷起处于动平衡状态；绿色区域为颗粒悬浮区，沉降使得支撑剂分布不均匀，该区域内支撑剂体积分数与注入携砂液中的支撑剂体积分数相近；蓝色区域为无砂区，支撑剂颗粒完全下沉，只留有基液，颗粒含量可忽略不计[19]。对比图5实验结果，支撑剂分布形貌相似，仅在90 s时，模拟结果与实验结果相差较大，这主要是实验时压裂液内的砂比不均匀，在刚开始时，进入平板裂缝内的支撑剂较少，形成的砂堤较低且较为平缓，随着时间的推移，实验与模拟结果的砂堤形态比较相似。两者差异的主要原因有：实验中颗粒大小为30/50目，模拟则采用的是平均粒径0.45 mm；实验中随着压裂液的减少，其流量也会发生变化，而模拟的流速始终保持不变。通过数值模拟与实验结果对比，此模型的计算结果与实验结果相对吻合，因此本次数值模拟可代替实验进行裂缝内流体的携砂研究。

2.2 压裂液流变参数对裂缝内砂堤分布的影响

基于第1节建立的数学模型，利用Fluent软件对裂缝内流体的携砂过程进行数值模拟研究。首先对清水的携砂过程进行了数值模拟，并以此作为对照组，在模拟时采用密度为1 800 kg/m3的球形陶粒支撑剂，粒径为0.6 mm，清水的黏度为1 mPa·s，密度为1 000 kg/m3。Cross清洁压裂液的零剪切黏度η0=1.5 Pa·s，流态指数n=-0.1，松弛时间λ=0.9 s，压裂液与支撑剂的流速都为1 m/s，砂含量为5%。对比清水与清洁压裂液在300 s时裂缝内支撑剂的铺置行为，结果如图7所示。

图7 300 s时压裂液携砂体积分数云图Fig.7 Sand volume fraction nephogram of fracturing fluid at 300 s

理想的压裂液要能将支撑剂尽量运移至裂缝远端，由图7可以看出，经过300 s时压裂液内砂堤达到平衡高度，支撑剂在裂缝顶端与平衡高度之间的高流速通道内向裂缝远端运移。清水内砂堤平衡高度达到19.2 cm，平衡距离从距入口处的10.5 cm延伸到62.4 cm，形成的砂堤占整个裂缝的体积较大,其平衡高度达到裂缝高度的96%。支撑剂在Cross清洁压裂液内分散均匀，砂堤形态长而平缓。平衡高度仅有9.8 cm，保持在裂缝高度的50%以下，大量支撑剂悬浮在平衡高度和裂缝顶部区域。从图8速度矢量图上可以看出，Cross清洁压裂液在入口处的流动呈现旋涡状，这种流动有助于卷起入口处的支撑剂向裂缝远端运移，从而降低砂堤的平衡高度，将支撑剂输运至裂缝远端。

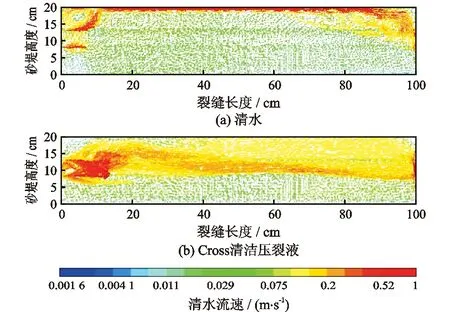
图8 300 s时压裂液速度矢量图Fig.8 Flow velocity vector of fracturing fluid at 300 s

以公式(13)描述的Cross流体本构方程为基础，通过改变零剪切黏度η0、流态指数n、松弛时间λ，研究不同参数对Cross流体携砂的影响。每组模拟600 s，裂缝内的砂堤形态都已达到稳定状态。不同本构参数下裂缝内砂堤分布如图9所示。

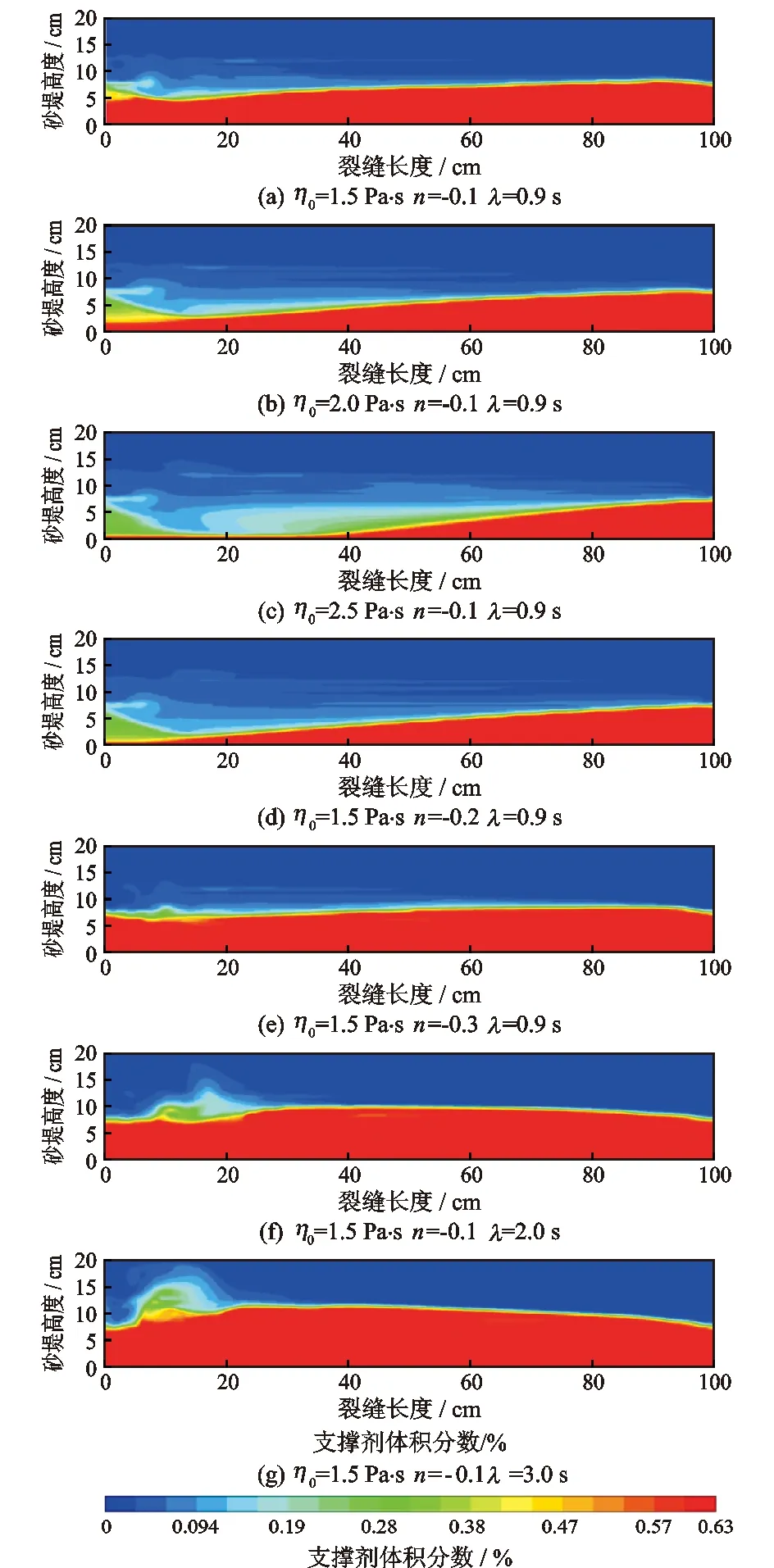
图9 Cross本构参数对裂缝内支撑剂铺置行为的影响Fig.9 Influence of Cross constitutive parameters on migration behavior of proppant in crack

进一步对比不同参数下支撑剂的铺置行为。由图10可以看出，仅改变Cross清洁压裂液的零剪切黏度，当零剪切黏度为1.5 Pa·s 时，支撑剂分布在裂缝的中前端，砂堤角度较大。零剪切黏度增加到2.5 Pa·s 时，支撑剂在裂缝中的水平携带力和浮力提升，支撑剂所受沉降速度降低。整体而言，随着零剪切黏度η0的增加，砂堤的坡度越来越陡，入口砂堤高度从4.32 cm降低到1.51 cm，再到0.37 cm。零剪切黏度越大，入口砂堤高度越低，不容易出现砂堵，携砂性越好。水平方向上砂堤的堆积厚度随裂缝的延伸缓慢增加，随着零剪切黏度η0的增大，支撑剂在整个裂缝中的含量减小，更多的支撑剂被运移到裂缝的远端。仅改变Cross流体流态指数n，支撑剂的分布形貌如图11所示。随着流态指数的减小，入口处的砂堤厚度逐渐升高，从0.54 cm升高到4.32 cm再到6.85 cm，支撑剂在入口处聚集沉降。水平方向上砂堤的高度随着裂缝长度的增加而缓慢增加。仅改变Cross流体的松弛时间λ，如图12所示，随着松弛时间λ的增加，支撑剂在裂缝内的含量增加，砂堤平衡高度上升，且平衡高度出现的位置逐渐向入口处靠近，大量颗粒在此沉降聚集，导致支撑剂过流面积逐渐减小，容易出现砂堵[20]。

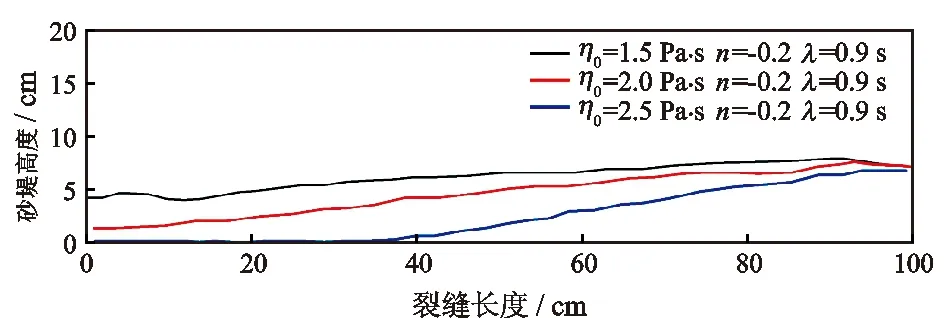
图10 改变η0对裂缝内砂堤形态的影响Fig.10 Effect of η0 on the shape of sand dike in crack

图11 改变n对裂缝内砂堤形态的影响Fig.11 Effect of n on the shape of sand dike in crack

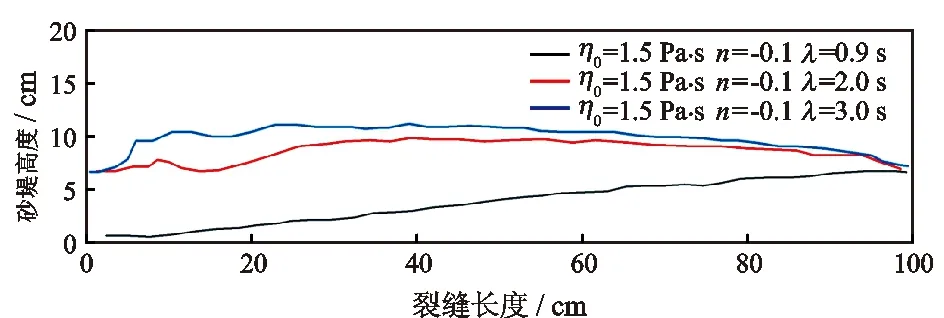
图12 改变λ对裂缝内砂堤形态的影响Fig.12 Effect of λ on the shape of sand dike in crack

综上所述，提高Cross流体的零剪切黏度、流态指数，减小流体的松弛时间，可有效降低砂堤的平衡高度，延长压裂液入口到砂堤平衡高度间的距离。从微观角度分析，零剪切黏度η0越大，表面活性剂压裂液内部的胶束缠绕强度越高，胶束有序排列形成稳定的网状结构；松弛时间越小，则流体发生剪切稀化时的临界剪切速率越大，胶束结构越稳定，从而提高了流体的携砂能力[21]。

2.3 支撑剂物性参数对其在裂缝内分布的影响

除了流体性质对裂缝内砂堤堆积高度有影响外，支撑剂的粒径和密度也会对砂堤的平衡高度产生重要影响，固定Cross流体的零剪切黏度为η0=1.5 Pa·s、流态指数n=-0.1，松弛时间λ=0.9 s，探索支撑剂物性参数对其在裂缝内分布的影响。

固定支撑剂密度，改变粒径，达到砂堤平衡时颗粒的分布形貌如图13所示。随着支撑剂粒径增大，颗粒沉降速度加大，平衡状态时的砂堤平衡高度升高且向裂缝入口处靠近。距离裂缝入口越近，砂堤形成平衡高度所需的平衡时间也就越短，压裂液携砂性能越差。

图13 改变支撑剂粒径对裂缝内砂堤形态的影响Fig.13 Effect of proppant particle size on the shape of sand dike in crack

固定支撑剂粒径，对密度不同的3种常用支撑剂进行对比分析，支撑剂分别选用密度1 500 kg/m3的轻质陶粒，密度为1 800 kg/m3的硬质陶粒以及密度为2 650 kg/m3的石英砂。不同类型的支撑剂在裂缝内的分布如图14所示。轻质陶粒可将砂堤平衡高度降低到裂缝高度的38%以下。颗粒支撑剂密度越大，砂堤前缘距离裂缝入口越近，砂堤前缘的角度越大，平衡高度也相应增大。这主要是因为支撑剂受到重力增大的作用，颗粒沉降趋势增加，导致砂堤迅速堆积。

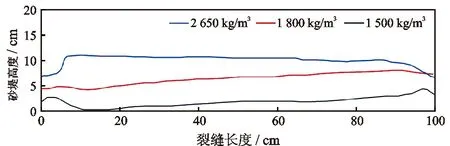
图14 改变支撑剂密度对裂缝内砂堤形态的影响Fig.14 Effect of proppant density on the shape of sand dike in crack

模拟结果表明，在清洁压裂液实际应用中，应优先选取小粒径、低密度的支撑剂。小粒径支撑剂在压裂液中容易出现卷起翻滚的现象，支撑剂可以被运送到更远的地方，平衡状态时形成的平衡高度较小，砂堤前缘距离裂缝入口的距离较大，形成平缓的砂堤[22]。低密度的支撑剂沉降速度较小，便于被压裂液带到裂缝远端，降低砂堵风险，避免出现裂缝上部产生无效支撑的现象[23]。

3 结 论

(1)通过与颗粒群在裂缝内运移实验对比，表明基于Cross流体本构方程，结合Eular-granular颗粒动力学方法，可以较为准确地描述清洁压裂液中颗粒群运移行为特性。

(2)基于Cross本构方程和颗粒动力学理论，对比分析了清洁压裂液与清水的携砂效果，支撑剂在清水内运移的砂堤高度可达到缝高的96%，而通过改变Cross流体参数模拟支撑剂在裂缝内的运移形貌后发现：增加零剪切黏度和流态指数，减少松弛时间，都可以将砂堤的平衡高度降低到总缝高的50%以下，从而使得压裂液在裂缝内的携砂性能得到大幅提高。

(3)支撑剂的物性对其在裂缝内的分布也有影响，固定Cross流体的零剪切黏度为η0=1.5 Pa·s、流态指数n=-0.1，松弛时间λ=0.9 s，采用低砂比、低密度、小粒径的支撑剂可将相同压裂液参数下的缝内携砂平衡高度降低到总缝高的38%以下，延长入口与支撑剂平衡高度之间的铺置距离，减小砂堵风险，提高压裂液的携砂能力。