泥页岩多场耦合流变模型

王 萍，张燕明，吕 杨，梁凌云，崔云群，屈 展，刘利锋，李树生

(1.西安石油大学 石油工程学院，陕西 西安 710065； 2.陕西省油气井及储层渗流与岩石力学重点实验室，陕西 西安 710065；3.低渗透油气田勘探开发国家工程实验室，陕西 西安 710018； 4.长庆油田分公司 油气工艺研究院，陕西 西安 710018； 5.长庆油田分公司 第五采气厂，陕西 西安 710018)

引 言

井壁失稳问题经历了从力学研究、化学研究到力学与化学耦合研究，由Chenevert、Gray和Darley[1-3]提出：井壁失稳的一个重要原因是泥页岩水化，而不单单是纯力学问题。此后，研究人员开始对黏土矿物的水化问题如泥页岩水化对井壁稳定性的影响展开研究。Chenevert[1]通过总吸附水量相关法对泥页岩进行了力-化耦合的定量分析，Hale和Mody[4-5]通过半透膜渗透压理论，将井底化学场的影响因素等效为孔隙压力，首次提出等效孔隙压力法。Tan[6-9]认为岩体内流体流动的动力主要靠孔隙压力与渗透压力共同作用下的总水势差导致的，依据岩石中引入水介质的连续性方程进而推导出膨胀性岩体中的流体运动方程。虽然国内外学者就泥页岩水化问题进行了大量的研究，但是由于问题本身具有复杂性，所得出的研究成果并不一致，仍然存在着许多疑问。如有些研究者认为总吸附水量影响着所有的水化变化，事实上用“总吸附水”概括这是不准确的，因为泥页岩中还存在着与水化反应无关的水分子，如渗透水化水、离子水化水、孔隙自由水等。总水势模型的溶质流动参数难以确定，且没有给出解决的方法。等效孔隙压力法以半透膜渗透压为出发点，引入“非理想半透膜”，在力学分析中将化学因素的影响定量化，实现力学与化学的耦合计算[10-12]。

在泥页岩井壁稳定性分析中，通常从力学、化学以及力学与化学耦合几个方面进行研究，然而这些研究往往很少考虑岩石的流变特性和初始微缺陷造成的损伤及其耦合发生过程中的演化扩展。泥页岩与钻井液相互作用，在其内部将会产生一系列的物理化学变化，改变岩石物质内部结构与力学性能，使岩石具有明显的流变特征。随着含水量的增加，岩石的流变更为明显，在一定的条件下可能会造成井眼缩径、卡钻、坍塌。为此，本文用经典半透膜渗透理论方法，通过将泥页岩与钻井液间的化学作用过程产生的应力引入到有效应力中，进行力学与化学的耦合计算，然后基于多孔介质有效应力原理，从岩石应力场、化学场、渗流场耦合分析的基本方程——平衡方程、连续性方程入手，建立泥页岩应力场、化学场与渗流场耦合作用下的流变分析模型。

1 泥页岩多场耦合流变模型

在建立泥页岩的流变分析模型时假设：⑴ 所研究泥页岩属微小变形，泊松比不变；⑵ 岩体所有初始微缺陷统称为“孔隙”，将泥页岩视为等效连续介质或具有初始损伤的连续介质；(3)钻井液是微可压缩流体，渗流服从达西定律；(4)结合渗透系数与流变参数之间的联系，在数值模拟计算时，每2个时步对渗透系数修正一次[13-14]。

对于单重孔隙介质，最常采用的有效应力张量形式为

σij*=σij-αpδij，

(1)

式中：σij*是有效应力，Pa；σij是施加正应力，Pa；p为孔隙流体压力，Pa；δij为Kronecker符号；α为比奥系数(0<α≤1)。

根据泥页岩与钻井液间化学势差造成的应力,得到远场孔隙压力

(2)

式(2)负号可为正或负，因为近井地带的岩石孔隙压力可能比远场地层中的孔隙压力大，也可能小，要视钻井液与泥页岩中的水活度大小而定。

将式(2)代入式(1)得到在应力场、化学场与渗流场耦合作用条件下，岩石的有效应力[15]

(3)

(4)

在流变变形过程中，由总应变与黏弹性应变、黏塑性应变的关系可得

(5)

将式(5)代入式(4)，可得到多场耦合时的黏弹塑性本构关系：

(6)

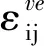
由岩石流变中的西原模型式(如图1)可知，在黏弹性体N//H(//表示两个原件并联)中，应力σ是应力σH与应力σN之和，而两者的应变相等。

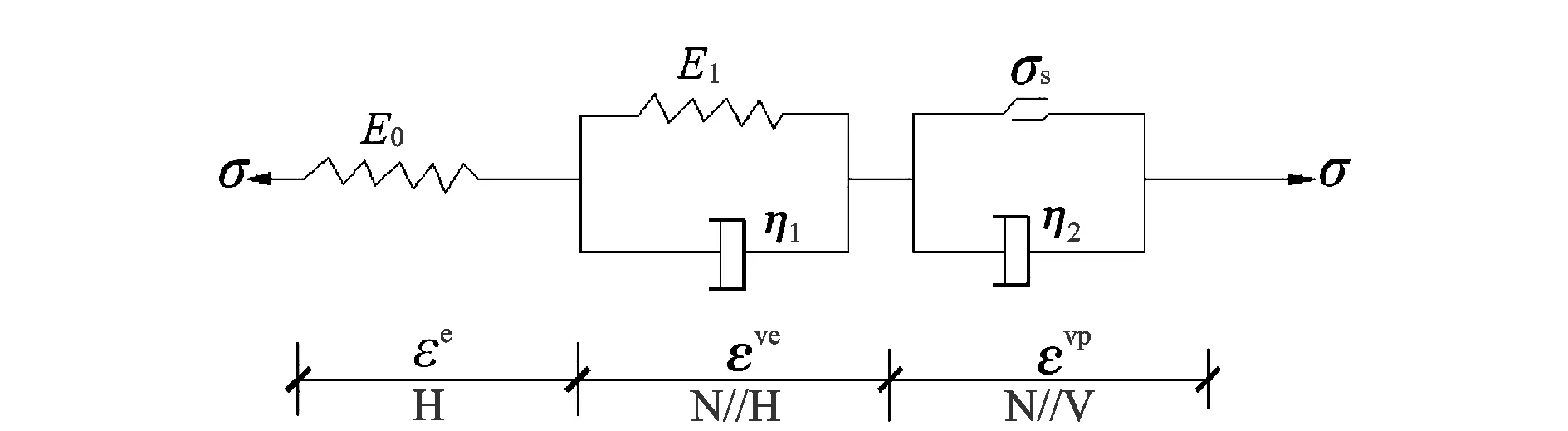
图1 岩石流变模型Fig.1 Rheological model of rock

即

(7)

整理得

(8)

若t=0时，εve=0，则在常应力σ=σs作用下求解方程

(9)

式中，E1为黏弹性体的黏弹性模量，η1为黏弹性体的黏滞系数。

则

(10)

式中，K*=K(1-DT)和G1*=G1(1-DT)为考虑初始水化损伤时，岩石蠕变的各项参数，其中，DT为岩石的初始水化损伤量，体积模量和黏性剪切模量分别为

式中，E0为弹性模量。

对于黏塑性变形部分，采用有效应力表述黏塑性蠕变。岩石黏塑性蠕变率可表示为

(11)

其中损伤参数Dc可由损伤率[11]

(12)

确定。式中，A、n为岩石材料常数，由实验确定；Dc为岩石蠕变损伤，σs为岩石屈服应力。

对式(12)进行积分得

(13)

据文献[16]、[17]并结合式(11)，则有

(14)

(15)

式中，F为岩石屈服函数，F0为岩石屈服函数的初始参考值。

将式(10)和式(15)代入式(6)，得到多场耦合流变本构方程为

(16)

2 流变分析的有限元格式

2.1 平衡方程

式(6)的矩阵格式为

{σ}=[D][∂]{f}-[D]({εve}+{εvp})-α{M}p+α{M}β，

(17)

可得到单元内任意点的总应力矢量的近似解为

(18)

(19)

式中，[∂]为算子矩阵，{σ}、{εe}分别为t时刻岩石内任意一点的应力和弹性应变，[D]为弹性矩阵，{M}=[1 1 1 0 0 0 ]T，

根据虚功原理可导出分析系统的平衡方程

(20)

将式(19)代入式(20)，得到

{Ru}e，简写为

[kuu]{δ}e+[kup]{p}e+[kuβ]={fve}e+{fvp}e+{Ru}e。

(21)

在Δtn=tn+1-tn内的位移、水压增量分别为{Δδ}3、{Δp}e，而黏弹性应变增量和黏塑性应变增量分别为{Δεve}e和{Δεvp}e，则平衡方程(21)的增量形式为

[kuu]{Δδ}e+[kup]{Δp}e+[kuβ]={Δfve}e+{Δfvp}e+{ΔRu}e，

(22)

式中：

对所有单元建立式(22)，形成整体平衡方程的增量形式为

[Kuu]{ΔU}+[Kup]{ΔP}+[Kuβ]={ΔRu}，

(23)

式中

{ΔRu}=∑({Δfve}e+{Δfvp}e+{ΔRu}e)。

2.2 连续性方程

泥页岩岩石是由岩石骨架、孔隙和流体所组成的多孔介质。一方面，岩石骨架与孔隙流体之间的摩擦力使孔隙流体的排出受阻，岩石变形延滞；另一方面，孔隙结合水的黏滞性使得骨架的变形有一个过程。由于岩石中水的存在和迁移使岩石变形特性既不是弹性体，也不是塑性体，而是黏弹塑性体。所以在泥页岩岩石发生蠕变的同时必然伴随孔隙中水的迁移。根据混合理论，分别建立岩石骨架、孔隙以及流体的控制方程，其次通过考虑方程之间的相互关联，最后得出岩石的连续性方程。因此，连续性方程可根据流体运动方程、物性状态方程及泥页岩骨架和流体的质量守恒方程来建立。

当有内部或外部的流体源时，上式变为

(24)

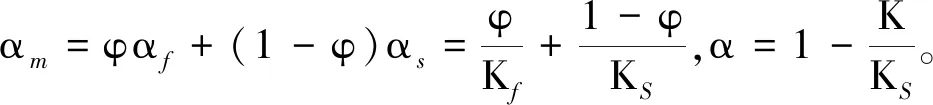
根据水压边界条件p=0和流速边界条件vn=0，将这2个边界条件代入达西定律表达式得

(25)

若某边界上法向流速或比流量已知，则该边界条件为

lvx+myy+nvz=vn。

(26)

代入达西定律得

(27)

式中vn为边界流体源矢量。将边界条件式(26)写成矩阵形式

(28)

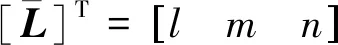
(29)

由流速边界条件式(29)，利用插值函数进行离散，由伽辽金变分原理得到

(30)

式中：

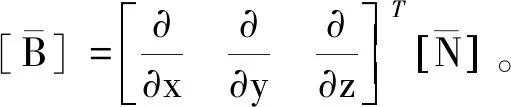
设tn到tn+1时刻单元结点的参数随时间变化后，采用时间积分的一般格式

(31)

(32)

式中θ为时间积分因子，其值域为0～1。

对所有单元建立式(32)，形成整体连续性方程

[Kup]T{ΔU}+[Kpp]{ΔP}={ΔRp}。

(33)

其中：

[Kpp]=∑([kp]+θΔt[kpp])；

{ΔRp}=∑Δt({Rp}e+θ{ΔRp}e-[kpp]{p}ne)。

2.3 总体控制方程

建立的多场耦合流变有限元平衡方程和连续性方程均具有耦合项，需联立求解[18]。因此，总体控制方程将由方程(23)和方程(33)组成，即

(34)

式(34)所给出的岩石流变多场耦合方程是一种应力场、化学场和渗流场耦合流变分析的统一形式，适用对符合西原流变模型的泥页岩进行多场耦合分析。考虑到泥页岩地层中的实际情况，针对不同的泥页岩井壁围岩耦合情况，当岩石受力状态或变形特性发生变化时，只需改变方程便可利用式(34)中的{ΔRu}计算格式，而连续性方程(33)保持不变，便可利用式(34)进行相应的多场耦合有限元分析。

若对泥页岩井壁进行黏弹性蠕变耦合分析，则只需取{Δεvp}=0，即有{Δfve}e=0，修正{ΔRu}，便可得到多场耦合的黏弹性分析计算公式：

{ΔRu}=∑({Δfve}e+{ΔRu}e)。

(35)

若对泥页岩井壁进行黏弹塑性蠕变耦合分析，根据式(19)有

后得到

{ΔRu}=∑({Δfve}e+{Δfvp}e+{ΔRu}e) 。

(36)

3 泥页岩多场耦合流变数值分析

泥页岩多场耦合模型的总体控制方程可由离散化的平衡方程和连续性方程得到，进而得出总体控制方程的有限元格式。通过二次开发子程序引入到ABAQUS中，并进行泥页岩井壁蠕变损伤失稳数值模拟分析[19-21]。

取长庆油田的长7层西峰233井区某井进行计算，其地层参数如下：井深H=3 400 m； 井眼半径rw=231 mm；地应力σH=38.5 MPa；最大水平主应力σ1=44.2 MPa；最小水平主应力σ3=35.8 MPa；地层原始内聚力C=18.7 MPa；地层原始内摩擦角φ=31.58°；地层泊松比μ=0.25；弹性模量E=31.25 GPa；吸水扩散系数Cf=0.013 4 cm2/h；有效应力系数α=0.4；吸水膨胀系数K1=0.033 3，K2=0.832。流变耦合分析采用西原模型，其中黏弹性模量E1=4 065 MPa，黏弹性系数η1=6 831 MPa·d，黏塑性系数η2=6 005 MPa·d。由实验测得不同时间的水化损伤量，见表1。

表1 不同时间岩石的水化损伤量Tab.1 Rock hydration damage at different times

由于是井眼围岩是轴对称形式，取1/4进行计算分析，建立模型长200 m、宽200 m、井径2 cm。经分析，边界对结果影响可以忽略，其模型和网格划分如图2。具体分析为：第一步，地应力平衡；第二步，钻进至目的层；第三步，围岩蠕变35 d。

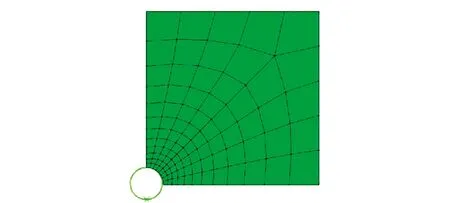
图2 围岩蠕变模型与网格划分Fig.2 Creep model of surrounding rockand its meshing

3.1 应力场变化

图3和图4分别为蠕变损伤分析开始到蠕变分析结束的井壁围岩的应力分布云图。由图3可知，在刚钻进至储层时，近井地带处于地应力平衡，此时，井内流体没有与储层发生接触。从图4可看出，泥页岩井壁围岩在多场耦合效应的作用下水化严重，出现垮塌现象。

图3 初始蠕变地应力平衡阶段Fig.3 Initial creep in-situ stress equilibrium stageS:各方向应力值

图4 蠕变损伤应力分布云图Fig.4 Stress nephogram of creep damageS:各方向应力值

井壁围岩蠕变损伤导致其变形具有明显的时效性和非线性，其蠕变损伤演化规律如图5所示。由图可直观地反映初始蠕变、等速蠕变和加速蠕变各阶段损伤值与时间的关系，体现了非线性蠕变损伤模型的特点。

图5 蠕变损伤演化曲线Fig.5 Creep damage evolution curve

岩石的蠕变损伤与其内部微裂纹的延伸和扩展密切相关，宏观表现为蠕变过程中的体积扩容。导致体积扩容的原因是由于井眼周围应力场的变化，即周向应力和径向应力的变化。多场耦合蠕变损伤产生的井周应力如图6所示。在加载阶段和初始变形阶段(t≤15 d)，不考虑蠕变损伤耦合分析和考虑蠕变损伤耦合分析中的径向应力和周向应力变化差别均不大，但在t>25 d以后，考虑蠕变损伤的井周应力变化比不考虑蠕变损伤的应力峰值大，且随时间差别扩大。这可以解释现场钻井不是立即坍塌，而是钻开后几天甚至半个月才出现破坏，此种破坏与时间有关，对钻井的危害也很大。

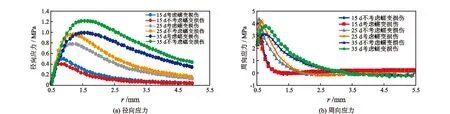
图6 多场耦合效应井周应力变化曲线Fig.6 Stress curves around well at different time under multi-field coupling effect

近井壁处由于长时间受多场耦合效应作用，井周应力变化剧烈，考虑蠕变损伤的井周应力与不考虑蠕变损伤的井周应力具有明显的差别，应力变化具有非线性和时效性。应力最大值不在井壁上，而是在近井壁地带，随着与井眼间距离的增大径向应力和周向应力开始减小且趋于稳定。因此在井眼附近会形成应力集中，造成井眼破坏，导致井壁失稳。

3.2 孔隙压力的变化

本文将泥页岩与钻井液间的化学作用过程产生的应力作用等效为孔隙压力，即化学场的耦合效应由孔隙压力的变化来表征。耦合效应下孔隙压力与时间、井眼距离的变化关系如图7、图8所示。由图7可知，不考虑蠕变损伤的孔隙压力随着时间增大明显，后逐渐趋于平缓。而考虑蠕变损伤的孔隙压力先随着时间增大而后开始缓慢下降。由图8可知，距离井眼越远孔隙压力越大，考虑蠕变损伤前期的孔隙压力较之不考虑蠕变增幅较快，后期增幅减小。岩石骨架的变形，导致孔隙结构和岩石孔隙体积的改变，造成孔隙压力发生改变。不考虑蠕变损伤时则忽略了岩石骨架变形的影响，相对于考虑蠕变损伤时孔隙压力大。这种变形是孔隙流体的长时间作用下由多孔介质的流变效应导致的，因此随着时间的增加孔隙压力差别越明显。

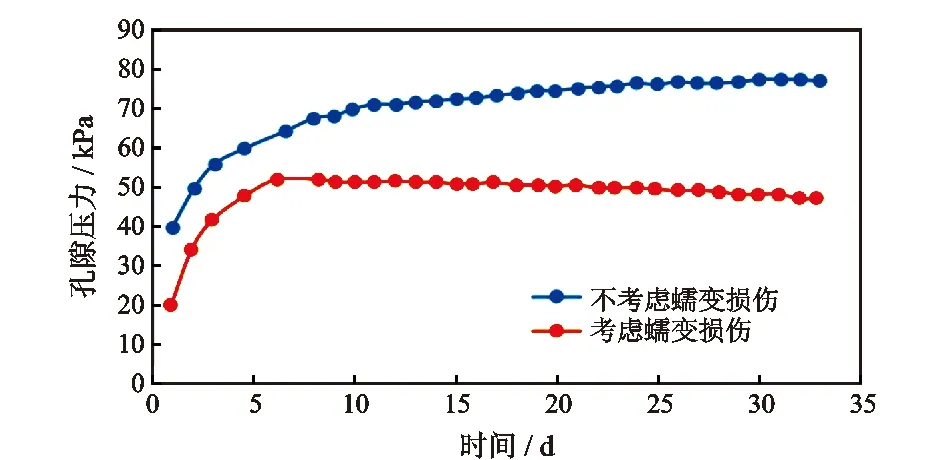
图7 孔隙压力-时间曲线Fig.7 Pore pressure-time curves

图8 孔隙压力-井眼距离曲线Fig.8 Pore pressure-borehole distance curves

3.3 渗透率的变化

渗透率的变化特性也可以直接或间接地反映出岩石内部渗流场的分布，如图9所示。岩石的蠕变损伤与其内部微裂纹的延伸和扩展密切相关，宏观表现为蠕变过程中的体积扩容。由图9可知，不考虑蠕变损伤的井壁围岩应变、渗透率随着钻进时间增大，这是因为泥页岩吸水后发生膨胀，应力增大裂隙或孔隙发生扩展，导致体积应变增大，同时形成一定的渗透通道。

图9 渗透率/应变-时间曲线Fig.9 Permeability/strain-time curves

考虑蠕变损伤，在初期蠕变变形阶段，岩石内微裂纹随机扩展增加，当微裂纹的扩展数量及长度达到一定程度后不再发生显著变化，则使得渗透率变化趋势变小，也说明蠕变变形进入稳态阶段，同时这也解释了在长期地应力作用下岩石内孔隙和微裂隙受压闭合而导致渗透率变小的现象。当渗透率随着时间推移达到某一最低值后会有一段增幅期，进入了加速蠕变阶段，在这一阶段岩石裂纹在随着水平应力逐渐变大的同时，其内部微裂隙继续迸发、延伸、贯通及扩展成为宏观裂缝。在非线性蠕变损伤变形期，随着轴向应力增大，岩石渗透率缓慢增加，当围岩发生失稳破坏时出现较大的阶跃。因此，岩石蠕变损伤(微破裂)演化引起渗透率的变化与岩体的蠕变损伤是一致的。

4 结 论

(1)井壁围岩蠕变损伤导致其变形具有明显的时效性和非线性特性，井周应力在整个蠕变损伤阶段的变化比不考虑蠕变损伤的应力峰值大，且随时间增加它们之间的差别扩大，此种破坏与时间有关，对钻井的危害大。

(2)应力最大值不在井壁上，而是在近井壁地带，随着与井眼距离的增大，径向应力和周向应力开始减小且趋于稳定。在井眼附近会形成应力集中，造成井眼破坏，导致井壁失稳。

(3)在孔隙流体的长时间作用下多孔介质产生流变效应，导致了岩石孔隙结构和孔隙体积的改变，造成孔隙压力发生改变。孔隙压力随时间、距离的增长而增大后趋于平衡。

(4)在整个蠕变阶段，围岩的渗透率先减小后增大。岩石蠕变损伤发展引起渗透率的变化与岩石的裂缝扩展是一致的。