一类非自治奇异摄动系统响应解的存在性

张淑芳,张新丽

(青岛科技大学 数理学院,山东 青岛266061)

奇异扰动系统出现在很多领域,包括生物化学动力学、遗传学、等离子体物理学、以及涉及大阻尼和阻力的机械和电气系统[1]。系统中的x和y是多维向量。系统(1)的周期解和拟周期解的存在性一直都是常微分方程定性理论中最受关注的问题之一。该问题早期的贡献来自于FLATTO和LEVINSON[2]。当函数F和G关于t是周期的,他们证明了系统周期解的存在性,并说明此周期解当正常数ε趋于零时趋于退化问题的周期解。HALE等[3]和CHANG等[4]将FLATTO和LEVINSON的结果推广到概周期情形,并给出了系统概周期解存在的充分条件。SMIT H等[5]不仅研究了非自治系统的概周期解,还讨论了这些解的稳定性。

据所知系统的拟周期解目前为止还没有被研究。在ZHU等[6]的工作基础上,本研究系统响应解的存在性,响应解就是与系统同频率的拟周期解,其中x,y是实数集上的未知函数,ε是一个正的小实参数,函数F和G关于t是拟周期的,频率为ω＝(ω1,ω2,…,ωd)。连续拟周期函数是概周期函数的特殊情况,但当假设F和G关于t是拟周期时,利用文献[3-5]的方法无法得到拟周期解的存在性。BERGER和CHEN[7]提出的拟周期函数的B-性质是解决这一问题的有效工具。

1 预备知识

假设系统

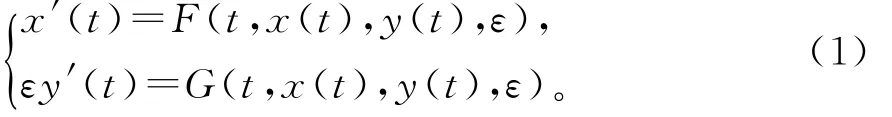
其中F和G关于t,x,y是C1的,而且满足F(t,0,0,0)≡G(t,0,0,0)≡0,则系统(1)对应退化系统

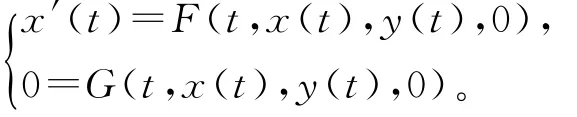
在ε＝0时有平凡解(x,y)＝(0,0)。将系统(1)在该平凡解处展开得到拟线性系统

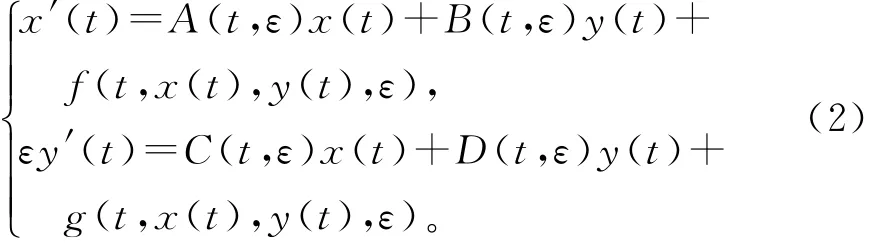
其中

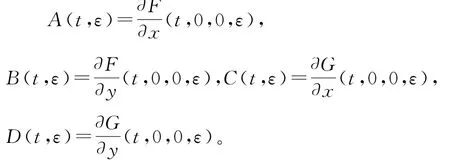
关于t是拟周期的而且关于t是一致连续的。假设当|x|,|y|很小时,非线性项f,g有关于t一致的小的Lipschitz常数,且当ε→0＋时,f(t,0,0,ε),g(t,0,0,ε)关于t一致趋于0。

首先,将给出一些引理,它们对证明主要结果很重要。

定义1[9]假设ω1,ω2,…,ωd是有理无关的,如果存在一个周期函数U＝U(θ1,θ2,…,θd),它关于θ1,θ2,…,θd是2π周期的,使得u(t)＝U(ω1t,ω2t,…,ωdt),∀t∈R,则连续函数u(t)是频率为ω1,ω2,…,ωd的拟周期函数。

注1 拟周期函数定义在很多文献中都有,例如文献[10]。显然这个定义等价于文献[7]的定义。

定义2[7]称函数H:R→R在实数集ω1,ω2,…,ωd有上具有B-性质,如果

i)H在R上是连续的,

ii)对于每个ε＞0,有δ＝δ(ε)＞0,使得若一个实数τ满足Diophantine不等式

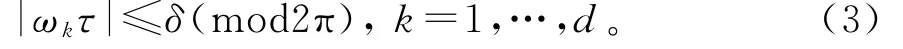
则τ是H的ε转移数,即

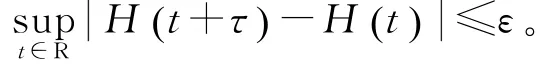
引理1[7]假设H(t)是周期为{2π/ω1,…,2π/ωd}的拟周期函数,则H(t)在{ω1,ω2,…,ωd}上有B-性质。反之,如果H(t)在集{ω1,ω2,…,ωd}的有限有理无关集上有B-性质,则H(t)是周期为{2π/ω1,…,2π/ωd}的拟周期函数。

用QPω表示R上频率为ω＝(ω1,ω2,…,ωd)的连续拟周期函数的线性空间。

定理1(QPω,‖·‖)在范数‖f‖＝下是一个Banach空间。

证明假设f n(t)∈QPω,(n＝1,2,…)是柯西序列,QPω是R上范数为的Banach空间C B(R)的子空间,且存在函数f0(t)∈C B(R),使得‖f n－f0‖→0,n→∞。因此对任意ε＞0,t∈R,存在K∈N,满足

由于f n(t)∈QPω,由引理1可知,f K(t)在(ω1,ω2,…,ωd)上具有B-性质。故对于ε,存在δ＞0,如果数τ满足不等式…,d),则对所有t∈R成立。此外

因此f0(t)在{ω1,ω2,…,ωd}上具有B-性质。因此f0(t)是拟周期函数,即f0(t)∈QPω。

推论1是范数‖(f,g)‖＝‖f‖＋‖g‖意义下的Banach空间。

引理2存在,使得对任意h(t)∈QPω,方程

有唯一解z(h,ε)(t)∈QPω,其中0＜ε≤ε0,D0＞0是个常数。更进一步,算子在QPω上是线性的,而且满足,映射在0＜ε≤ε0上是连续的。

证明容易验证函数

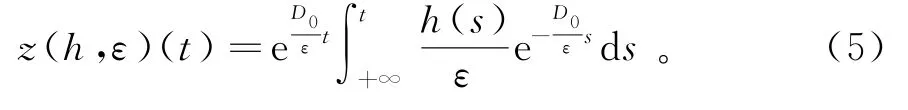
是(4)的解。因为h(t)∈QPω,由引理1得h(t)在上具有B-性质。假设实数τ满足式(3),是函数h(t)的任意ε平移数,有

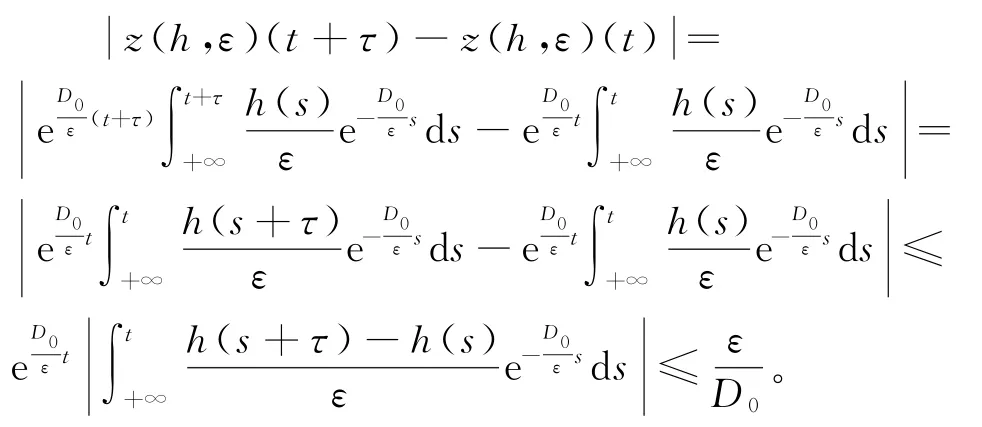
因此z(h,ε)(t)在{ω1,ω2,…,ωd}上具有B-性质,z(h,ε)(t)∈QPω。

以下来证唯一性,若方程(4)有另一个有界解,用z1(h,ε)(t)表示,则函数v(t)＝z(h,ε)(t)－z1(h,ε)(t)满足齐次方程εz′＝D0z,故有v(t)＝,其中c为常数。这就意味着如果c≠0,v(t)是无界的。这与z(h,ε)(t)和z1(h,ε)(t)的有界性矛盾。换句话说,z(h,ε)(t)∈QPω是式(4)的唯一解。

在QPω定义算子有以下形式

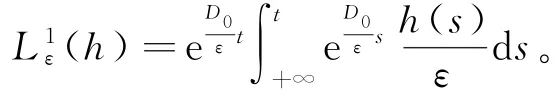
容易看出是线性有界的,即存在＞0使得关于ε一致成立。

以下证明引理2的最后一个结论,令u(t)＝z(h,ε)(t)－z(h,ε′)(t)满足

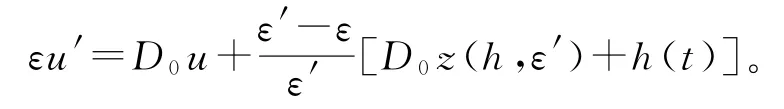
其中0＜ε,ε′＜ε0。由此可见

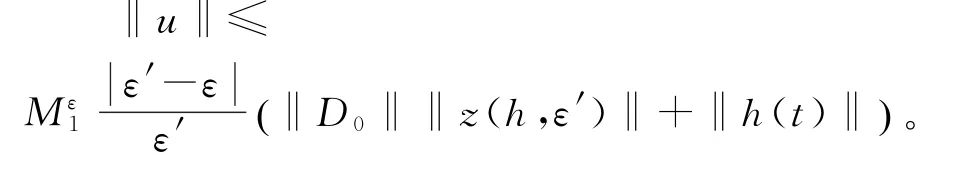
从而得到对0＜ε＜ε0,有映射是连续的。

与引理2的证明类似,得到以下引理。

引理3存在N＞0,对任意β(t)∈QPω,方程

有唯一解u(β)(t)∈QPω,其中A0＞0是个常数。更进一步,QPω中的算子∏:β→u(β)是线性的而且满足‖∏‖≤N。

2 主要结果

首先考虑非齐次方程

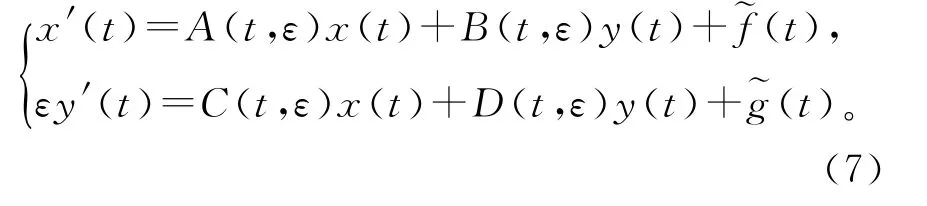
定理2假设

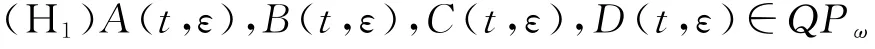
在(t,ε)∈R×[0,ε0]上有界且关于t一致连续。他们的界统一用来表示。

(H2)A(t,0)＝A0＞0,B(t,0)＝B0,C(t,0)＝C0＝0,D(t,0)＝D0＞0是常数。则存在满足0＜ε1＜ε0的ε1,使得任意满足0＜ε＜ε1的ε,系统(7)有唯一解

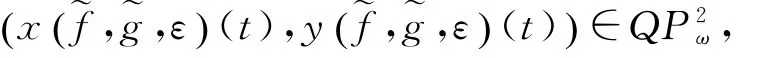
满足

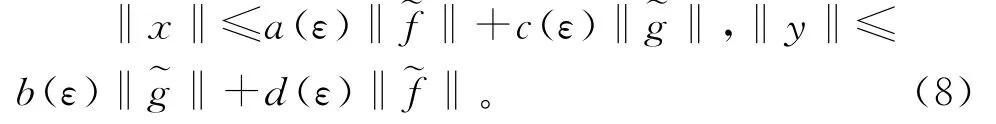
证明对于,考虑系统

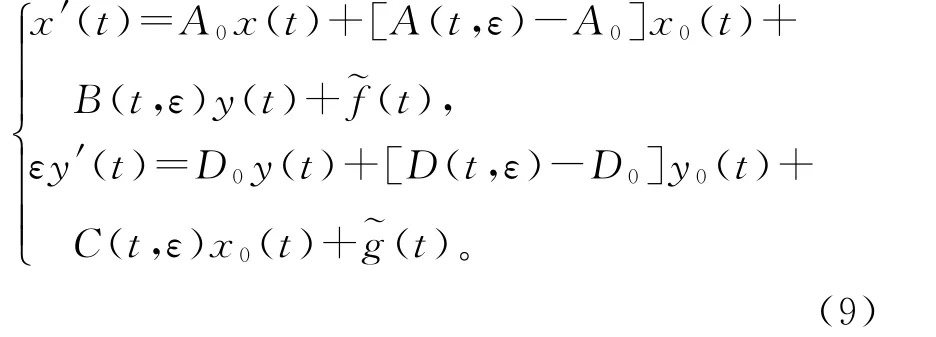
由引理2得系统(9)的第二个方程有唯一解y∈QPω。然后把y带入第一个方程中,由引理3,得到唯一解x∈QPω。故定义映射,即如果ε足够小,映射是压缩的。事实上,对任意,如果

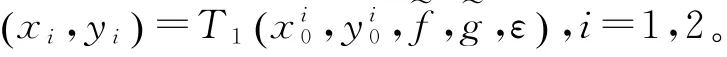
可以得到u＝x1－x2,v＝y1－y2满足

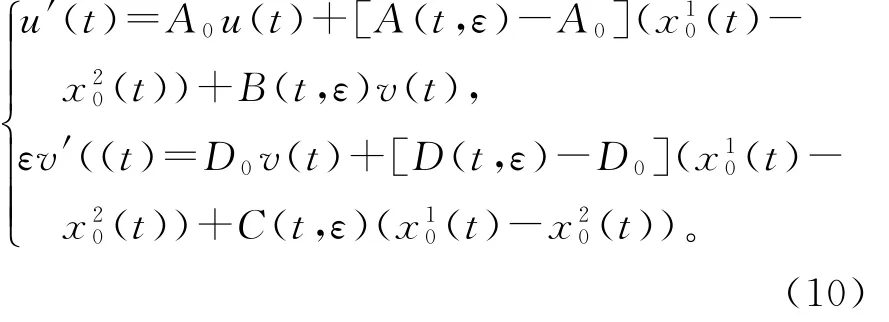
由引理2和引理3,得到

从而得出估计

因 为A t(,ε),B t(,ε),C t(,ε),D t(,ε)关 于t一致连续,对于任意ε∈(0 ,ε0),存在ε1≤ε0,使

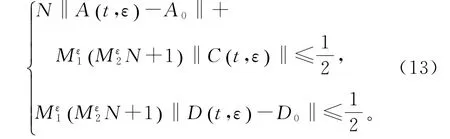
结合式(12)和(13),得出结论

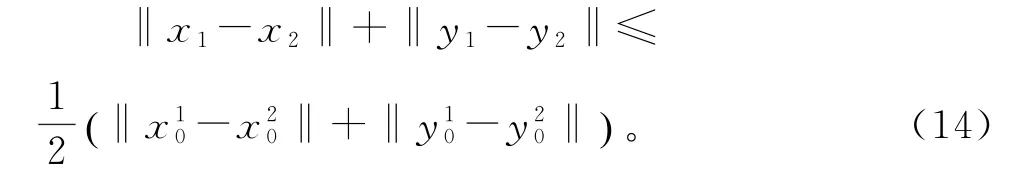
根据压缩映射原理,T1有唯一的不动点,且有

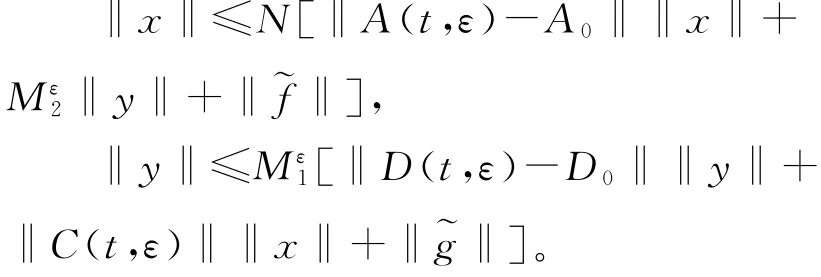
这意味着

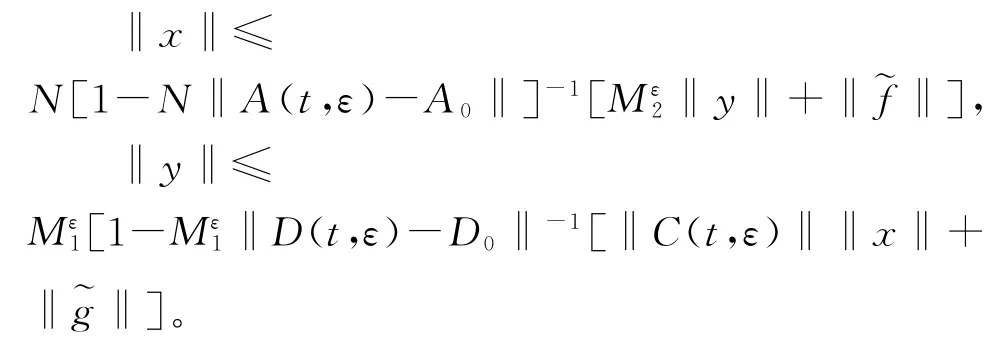
令

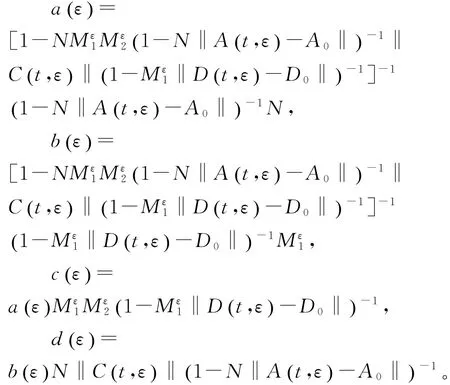
因 为A t(,ε),B t(,ε),C t(,ε),D t(,ε)关 于t一致连续,对于任意,存在足够小的ε1≤ε0,使得

则有如下估计

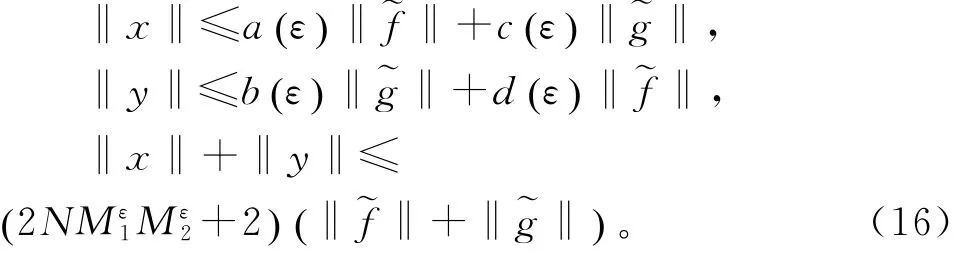
根据(14)和(16),只需证明定理的最后一个陈述。因为T1关于是线性无关的,则得到Kε()是上的线性算子。由(16)得到不等式如果对0＜ε＜ε1,

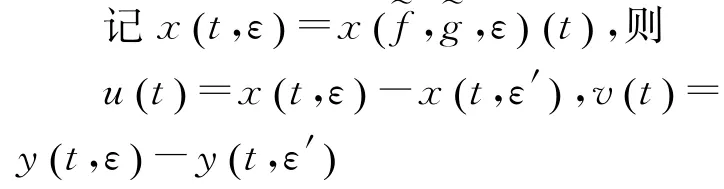
满足

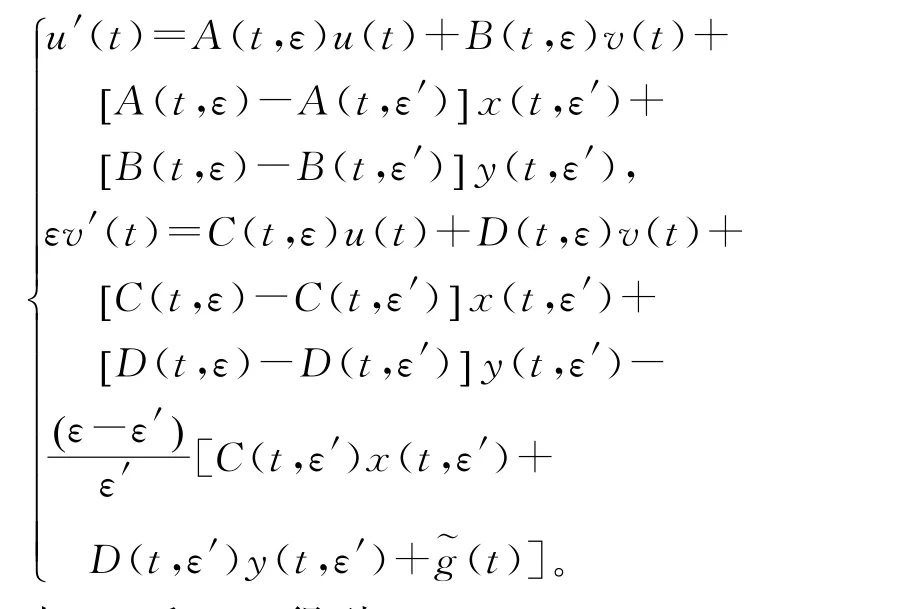
由(15)和(16)得到

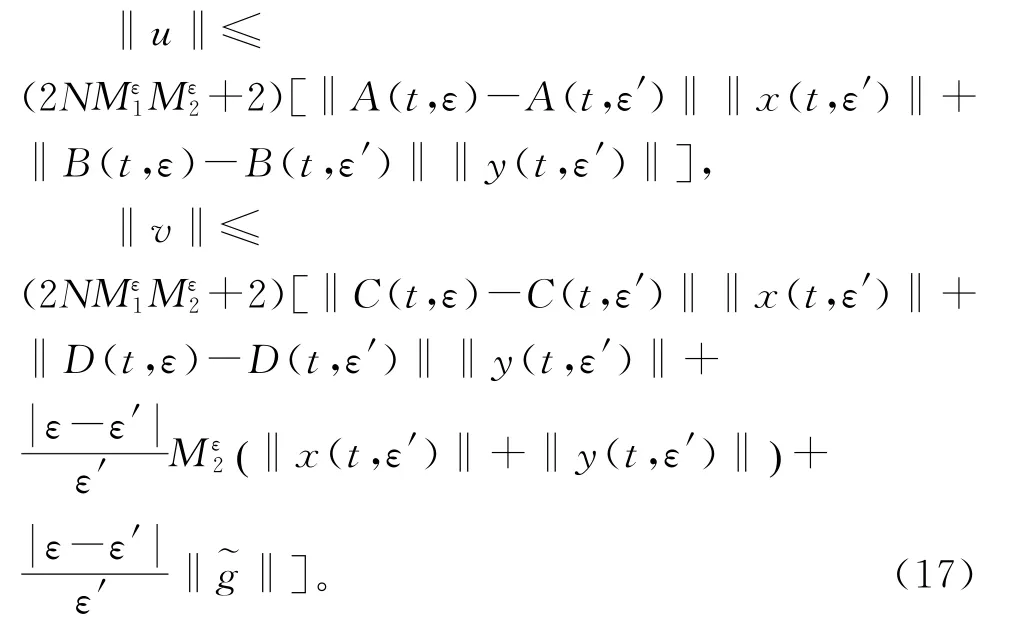
根据条件(H1)得到对0＜ε＜ε1,映射ε→Kε()是连续的。

现在考虑非线性系统(2),即

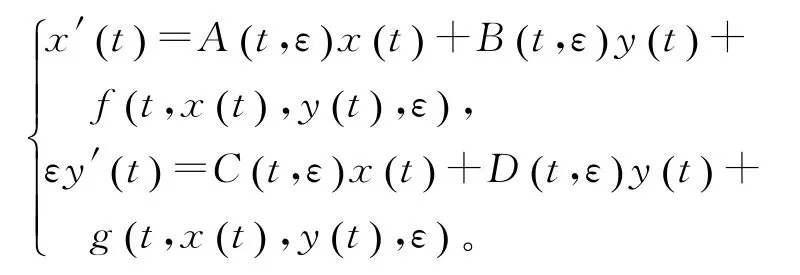
其中f(t,x(t),y(t),ε),g(t,x(t),y(t),ε)∈QPω。

根据SMIT H[5]的证明思路,证明如下定理。

定理3假设(H1)、(H2)和(H3)成立

(H3)函数f,g关于t( ,x,y,ε)是连续的,其中,是正常数,且对任意的t关于(x,y,ε)是一致连续。而且存在两个非递减函数Φε(),Ψε(,σ),满 足

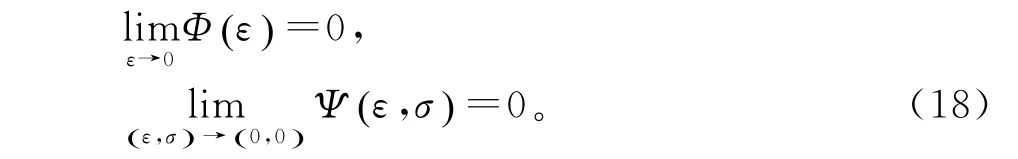
其中0≤ε≤ε0,0≤σ≤σ0,使得对

对所有t成立,则存在0≤ε2≤ε1,0≤σ1≤σ0,对任意满足0≤ε≤ε2的ε,系统(2)有唯一解满足

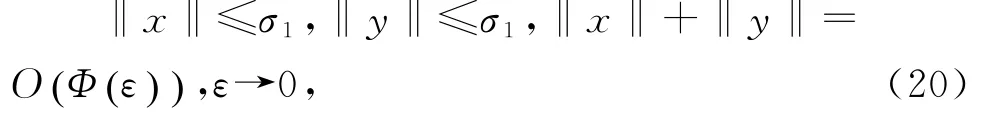
且对t∈R关于ε一致连续。

证明因为Φ,Ψ满足(18),故可选择0＜σ1＜σ0,0＜ε2＜ε1使得

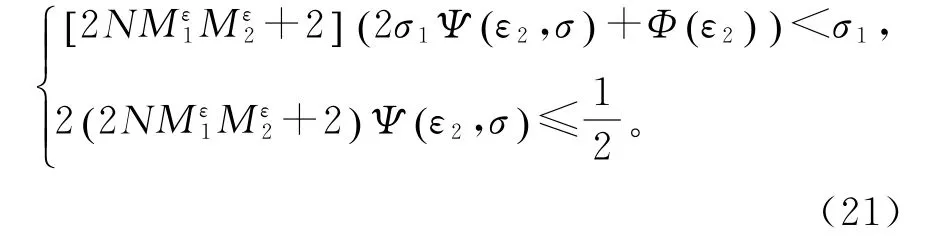
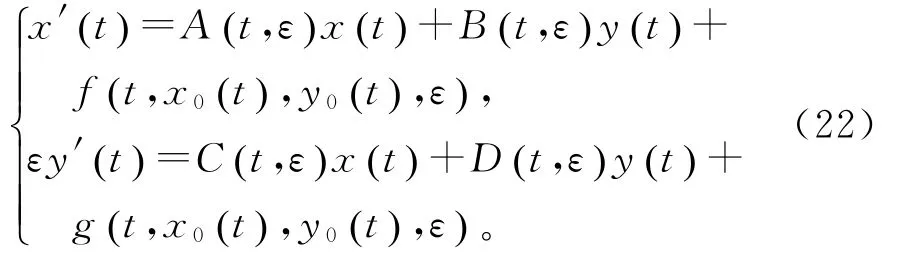
根据引理2和定理2,系统(22)有唯一解(x,y)∈QP2ω。根据条件(19)和Φε(),Ψε()的单调性,得估计

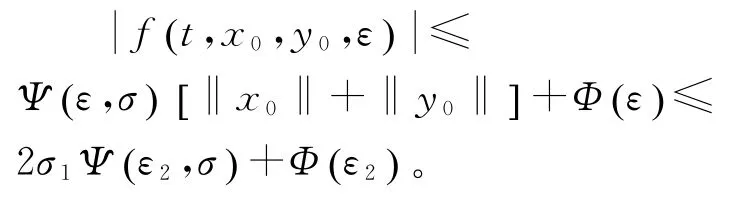
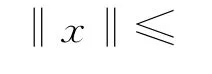
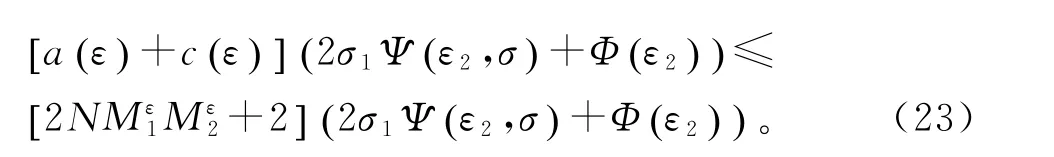
‖y‖的估计类似。如果,发现

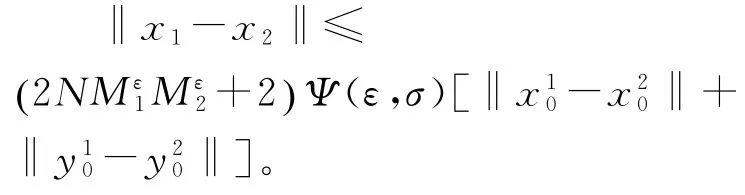
‖y‖的估计类似。故得如下结论

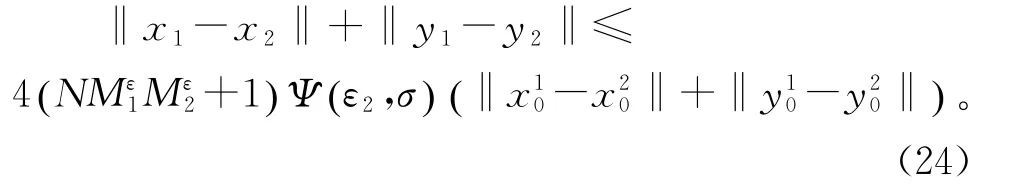
最后从定义系统中得到(x,y)的估计

故

3 结 语

考虑了一类非自治奇异摄动系统响应解的存在性问题。首先利用关键引理1证明了拟周期连续函数在上确界范数下形成一个巴拿赫空间;然后证明了线性方程解的存在唯一性;最后将系统非齐次系统(1)在它的平凡解处展成拟线性系统(2),并利用不动点定理和拟周期函数的B-性质,证明非自治的奇异摄动微分方程响应解的存在性和唯一性。拟周期函数的B-性质是研究拟周期奇异摄动系统解的适定性的有利工具。