汽车与护栏碰撞立柱绊阻机理及防止措施*

赵坤民，崔娜杰，赵德望，任大鑫，沈羡玉

（1.大连理工大学，大连 116024；2.合众新能源汽车有限公司，桐乡 314500；3.北汽股份有限公司，北京 101300）

前言

公路护栏在被汽车撞击后能够将碰撞车辆引导回正常路线，防止车辆越出路外或进入对向车道，同时可以吸收部分碰撞能量以降低对车内乘员的伤害，因此提高护栏的防撞安全性能具有重要意义。

根据护栏的刚度和变形进行分类，一般可分为刚性、柔性和半刚性3类护栏［1-3］。其中，半刚性波形梁护栏具有诸多优势：碰撞后波纹的延展可以吸收较多能量，有较好的视线诱导性，外形也较为美观，且零部件较易更换。因此，在我国使用最为广泛［4］。

波形梁护栏由两波型或三波型护栏板、护栏立柱和缓冲块组成，具备一定刚性和柔性。在汽车与护栏碰撞过程中，护栏变形吸收碰撞能量，同时引导车辆的行驶方向，最大程度降低对车内乘员的伤害。

国内外众多学者和机构自20世纪80年代开展了车辆与护栏碰撞特性的研究，对护栏的设计提供了大量的借鉴和经验。美国国家交通研究所对护栏的形式选择和结构设计做了深入研究，出台了评估高速公路上护栏性能的标准［5］。Alluri等［6］分析研究了G4型波形梁护栏和缆索护栏的防撞性能，基于不同车型和不同碰撞工况对两者进行了对比，结果显示G4型波形梁护栏性能优于缆索护栏。Lee等［7］提出了三维土柱模型，考虑车辆在撞击过程中与土壤的相互作用，探究了圆形、方形和C型3种立柱的性能，结果表明圆形立柱的护栏系统变形量最小。Yang等［8］利用ADAMS软件研究了客车与半刚性护栏的碰撞性能，结果表明当速度小于80 km∕h时，该护栏在变形量和导向性方面都有较好的效果。雷正保等［9-10］利用拓扑优化方法开发了以塑代钢PVC护栏和倒U形梁板，结果表明这两种类型的护栏均有较好效果且能满足法规指标要求。孙胜江等［11］提出了一种玄武岩纤维复合材料梁柱式护栏，结果表明该种护栏具有良好的导向性能。金思宇等［12］将护栏材料由金属钢板替换为玻纤增强聚丙烯热塑性复合材料，优化了护栏的上下沿高度。

国内外大多数学者对护栏的研究局限于特定路段的护栏防撞性能研究或探究新型材料，虽然可以达到一定效果，但是结构复杂，成本较高，推广范围受限，对于车轮绊阻成因及护栏整体优化研究较少，因此设计新型的经济适用护栏结构很有必要。

实车足尺碰撞试验是迄今为止对护栏的研究方法中最准确的，但是做一次试验就要耗费一辆汽车，且为采集数据要加装很多传感器和摄像机等昂贵设备，此外还要准备足够大的试验场地和足够多的工作人员；缩尺模型试验是将实车足尺碰撞的整个模型按照一定比例缩小，成本相对较低，可以方便更换参数，针对某一部分进行多组试验，但建立模型较困难，步骤也较繁琐，此方法应用并不广泛；计算机仿真在解决路侧安全问题中起到重要作用，LS⁃DYNA、MADYMO、PAM⁃CRASH、PC-CRASH、ADAMS等软件已经广泛用于汽车碰撞分析。

本文中运用有限元仿真技术，建立汽车与护栏碰撞的仿真模型，研究我国当前应用最广泛的波形梁护栏存在的缺点，探索立柱绊阻的形成机理和预防措施，并通过对立柱的改进和对主要部件的优化来提高汽车与护栏的碰撞安全性。

1 汽车-护栏碰撞仿真模型

首先使用HyperMesh软件建立有限元模型，然后使用LS⁃DYNA软件进行仿真计算，最后在HyperView和Hyper Graph2D软件中做数据处理和结果分析。

1.1 汽车有限元模型

我国汽车类型很多，电动化和轻量化是发展趋势，小型车深受欢迎。在高速公路上质量越小的汽车与护栏发生碰撞时越易发生下钻的危险姿态。基于这些考虑，选择1 300 kg左右的A0级汽车作为研究对象。图1示出某车型的有限元模型，整体尺寸 为4356 mm×1678 mm×1370 mm，整 体质 量 为1333 kg，共有339个部件，270 768个单元，283 859个节点。

图1 某车型的有限元模型和碰撞试验

首先需要验证有限元模型的正确性。由于C⁃NCAP碰撞试验较成熟，有许多试验和仿真结果可以参考，因此本文通过正碰仿真分析与试验结果对比来验证模型的正确性。根据我国正面碰撞法规的要求，设置车辆以50 km∕h的速度与正前方20 mm处的刚性墙进行0.15 s的碰撞［13-14］。碰撞过程中左侧B柱上方加速度随时间的变化曲线如图2所示，仿真结果基本符合真实情况，从而验证了有限元模型的正确性。

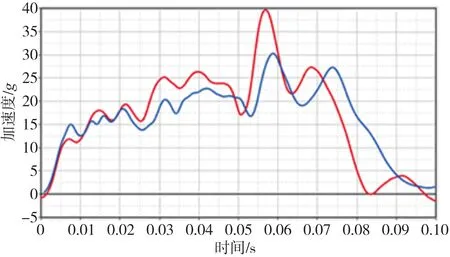
图2 车辆正碰过程中B柱上方加速度随时间的变化曲线（红色：仿真结果；蓝色：试验结果）

1.2 汽车-护栏碰撞有限元模型

护栏系统如图3所示，包括波形梁板、六角形防阻块、圆柱形立柱和地基等部分。立柱间距4 000 mm，埋入混凝土中，埋入深度不小于400 mm。梁板截面为W型，宽度310 mm，高度85 mm，厚度4 mm，与防阻块接触面宽度14 mm。防阻块截面为六边形，单边长约125 mm，纵向高度200 mm，厚度4.5 mm。圆柱形立柱，总长2 150 mm，直径140 mm，厚度4.5 mm，埋深1 400 mm，剩余750 mm在地面以上，防阻块安装孔位置距离地面600 mm。

图3 波形护栏及其模型

首先利用三维制图软件CATIA进行建模，并保存为IGS格式，在有限元软件HyperMesh中完成网格划分、材料选择和属性定义。

护栏各部件均为Q235碳素结构钢，材料模型选用分段弹塑性材料，即LS-DYNA软件中的24号材料，单元类型采用Belytschko-Tsay壳单元，平面内单点积分，厚度方向采用2~5个积分点。Q235钢的密度为7 860 kg∕m3，弹性模量为210 GPa，泊松比为0.3，材料的真应力应变曲线输入到HyperMesh中。

在汽车碰撞护栏过程中，梁板最先与汽车接触，随后通过其波形的展开吸收碰撞能量。根据大量的交通事故和实车足尺碰撞试验数据，可以发现轿车撞击波形梁板不会导致梁板的拼接螺栓失效［15］，因此在仿真分析中，可以将波形梁板设为无限长，不考虑梁板之间的拼接。连接护栏各部件的螺栓可能发生断裂失效，需要采用会失效的节点约束［16］，即在相连接的部件对应的节点约束自由度，焊点则用带失效条件的无质量梁单元来模拟，耦合6个自由度。

模拟立柱与地基相互作用的方法有3种［17-18］，其中直接约束立柱最大弯矩位置的方法具有计算效率高和结果可靠的优点，在实际工程应用中被广泛使用。经调研发现，立柱在地基下400 mm处产生最大弯矩，在搭建有限元模型时全约束所有立柱在此处的节点。

对于同一护栏型式，不同碰撞条件会影响护栏12跨以上的长度。小型轿车在碰撞护栏过程中，主要是与汽车接触的部分发生变形，其它部分变形很小，为降低跨数对计算的影响，本文中选11跨进行建模，护栏总长44 000 mm。

汽车与护栏碰撞的初始条件包括碰撞速度、碰撞角度和碰撞点。当发生碰撞事故时，驾驶员一般来不及采取制动措施，失控车辆会以一定速度和角度与护栏发生碰撞。统计数据显示大多情况下碰撞角度小于20°。至于碰撞点的选择，研究发现跨中并不是最合理的碰撞点［19］。根据我国最新颁布的实车碰撞试验标准，初始碰撞速度设为100 km∕h，碰撞角度为20°，碰撞点为两立柱间距的1∕3处。图4示出施加初始碰撞条件的轿车-护栏碰撞系统的有限元模型。

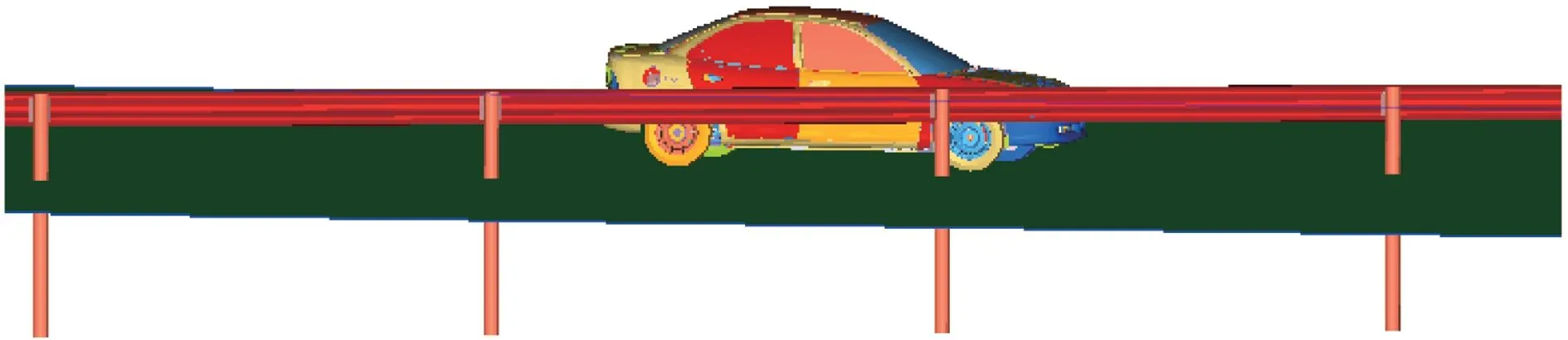
图4 轿车与护栏碰撞的有限元仿真模型

2 仿真结果分析

2.1 能量分析

在汽车与护栏碰撞过程中，护栏整体的速度较小，可以不分析护栏的动能，而只考虑汽车的动能。仿真结果显示，整个系统的内能增加了1.21×108J，护栏的内能增加了8.88×107J。由此可知，汽车变形吸收了总能量的23.3%，护栏变形吸收了其余的76.7%，其中梁板吸能35.0%，立柱吸能30.1%（碰撞点附近两立柱吸能27.8%，防阻块吸能11.6%）。

2.2 护栏变形分析

护栏整体变形情况如图5所示。梁板、防阻块和立柱均发生了较大变形，部件的连接在碰撞区发生了失效，防阻块脱离护栏板。碰撞发生后215 ms时，护栏横向变形达到最大值732.5 mm，之后由于回弹而有小部分回落。

图5 护栏整体变形情况

2.3 汽车行驶轨迹

图6 示出在碰撞过程中0、100、200、300、400和500 ms时刻汽车与护栏的状态。在碰撞初期，汽车右侧的翼子板和保险杠最先与护栏接触，在0-300 ms期间护栏变形逐渐增大，由于汽车所受到的横向作用力和纵向作用力的大小和方向不断改变，其行驶轨迹逐渐被修正。在300 ms时车身与护栏近似平行，护栏的导向功能基本完成。在接下来的时间内，汽车在惯性矩的作用下继续转向，在400 ms时车头离开护栏，500 ms时汽车整体已基本脱离护栏，碰撞过程结束。从图中可以看出，护栏对于汽车导向的全过程发挥了较好的修正作用。

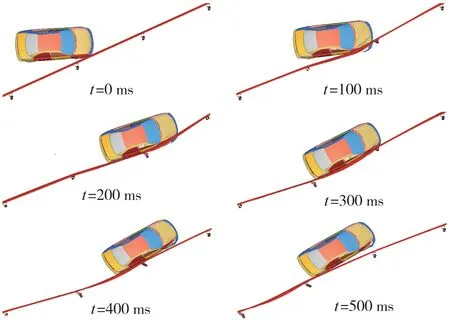
图6 汽车与护栏碰撞过程的行驶轨迹

2.4 立柱绊阻形成机理

在汽车与护栏碰撞过程中，立柱会发生横向位移与纵向弯曲，在某些情况下会绊阻车轮［20］。其形成机理如下：在碰撞初期，汽车最先接触梁板，梁板开始逐渐变形，随着碰撞的持续深入，梁板将碰撞力传递给立柱和防阻块，防阻块开始发生塑性变形，立柱在地面以下400 mm处形成塑性铰，此时立柱也开始发生塑性变形，当车轮行驶到立柱处，由于碰撞角度和摩擦等因素使立柱置于车轮的内侧，随后车轮外偏逐渐增加，形成了立柱对车轮的绊阻。立柱绊阻会扰乱汽车的运动轨迹，造成瞬间减速度过大，严重危害乘员安全，甚至会造成交通阻塞以及连环车祸。

图7 示出立柱对车轮绊阻的形成过程。汽车右前翼子板与护栏相接触，随着碰撞力的增大，汽车与护栏均开始变形且逐渐增大，碰撞点不断向立柱靠近。在125 ms时刻，防阻块被压扁后，与之最近的立柱的下端开始变形，整个立柱向下倒伏，在135 ms时刻，立柱对车轮形成第一次绊阻，且在165 ms时刻第一根立柱连接螺栓失效，接着在305 ms时刻，另一根立柱对车轮形成第二次绊阻（图中没有展示）。

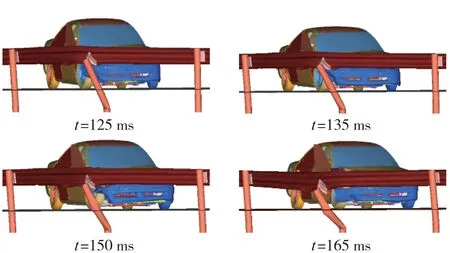
图7 立柱对车轮绊阻的形成过程

3 防绊阻立柱设计

为防止绊阻现象的发生，本文中提出了两种立柱改进方案。第一种为填充型立柱，即在空心圆筒立柱中填充泡沫材料，既能使立柱提高吸能性，又能对车辆起缓冲作用。第二种为N型弯曲立柱，即通过改变立柱的结构，增大立柱与梁板的横向距离，从而降低车辆与立柱接触的可能性，避免立柱对车轮形成绊阻。

3.1 填充型立柱

选用3种泡沫材料，即聚氨酯泡沫、聚亚安酯泡沫和聚丙烯泡沫，作为立柱填充物进行碰撞仿真分析，评价填充型立柱能否降低车辆的质心加速度。为简化计算，将整车简化为一个长方体质量块直接撞击立柱。

前文分析了护栏各部件的吸能比例，结果显示碰撞点附近的两个立柱共吸收总能量的27.8%，由于动能与质量成正比，可选整车质量1 300 kg的27.8%作为简化模型中质量块的质量，体积也按整车体积的27.8%计算，该质量块的质量为180 kg，体积为200 mm×200 mm×600 mm，以100 km∕h的速度撞击立柱。质量块采用实体单元划分，单元边长为10 mm，材料与立柱相同，均为Q235钢。立柱填充物也采用实体单元划分，由于立柱与填充物之间的摩擦所起的作用很小，为简化模型将立柱与填充物做共节点设置，不考虑二者之间的相互作用。立柱总高度为2 150 mm，碰撞中心的高度设置为1 950 mm，即护栏的螺栓连接位置。

质量块分别撞击填充了聚氨酯泡沫、聚亚安酯泡沫和聚丙烯泡沫的3个立柱，其质心最大加速度分别为34.2g、32.2g和33.3g，而质量块撞击原始立柱得到的质心最大加速度是35.3g，由此可知聚亚安酯泡沫填充立柱的安全性能高于原始立柱约9%。

图8 示出原始立柱和泡沫填充立柱在碰撞过程中的变形。由图可见，当质量块撞击立柱时，立柱会给质量块一个向上的作用力，使质量块不断上升，而在相同时间内填充立柱变化的倾角较小，从其根部的塑性变形情况来看，还有一定的变形空间，说明还可以承受更大的冲击。

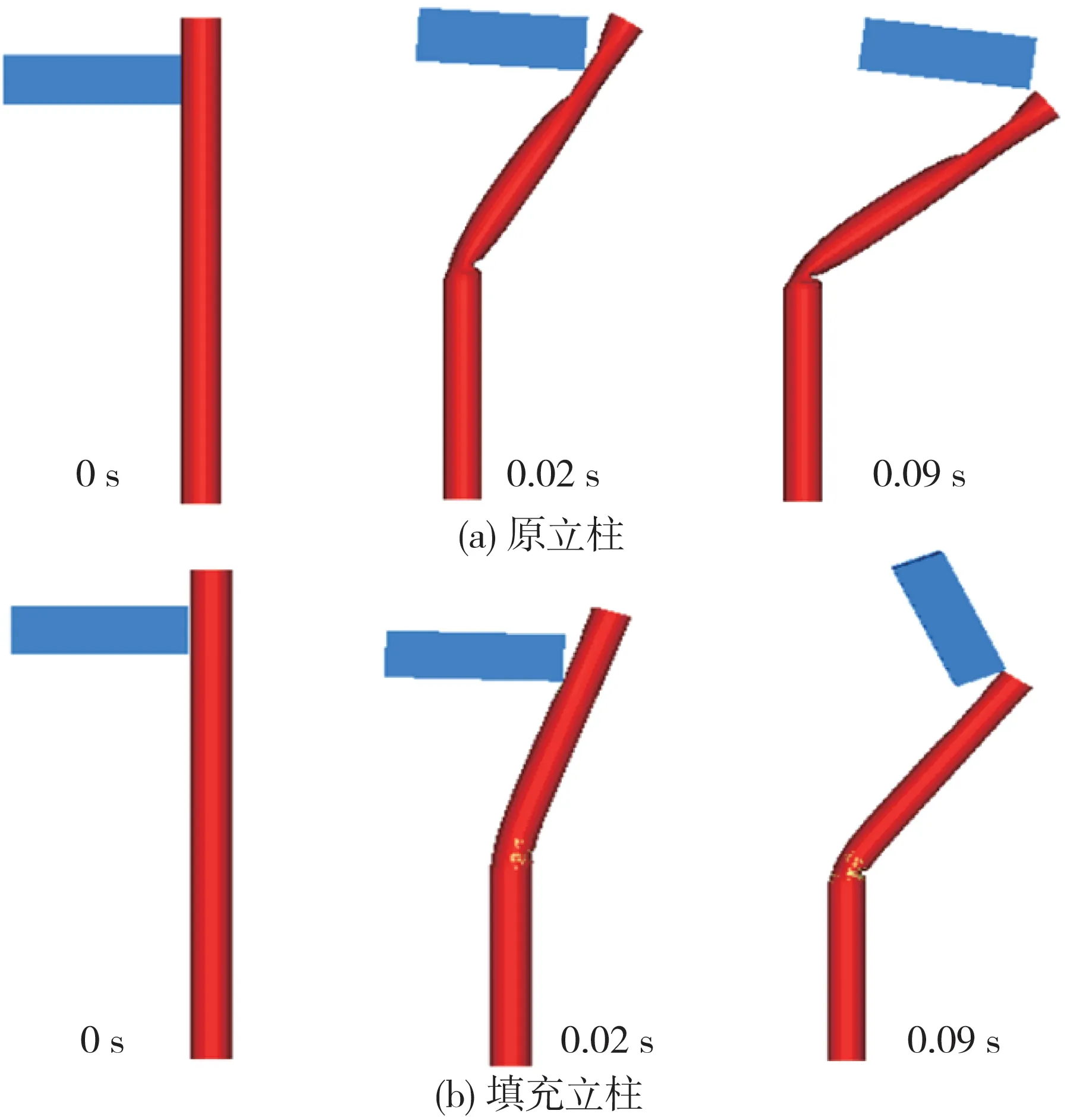
图8 原立柱和填充立柱碰撞变形

由于质量块变形很小，撞击动能的减少主要通过立柱的变形消耗。对比结果发现，原立柱和填充立柱分别吸收了1.34×107和1.56×107J的能量，说明填充立柱的吸能性更好，更有利于保护车辆。

3.2 N型弯曲立柱

如图9所示，N型弯曲立柱具有良好的抗弯性，被汽车撞击时不易产生扭转，同时给车轮提供一定避让空间，有助于避免绊阻发生。

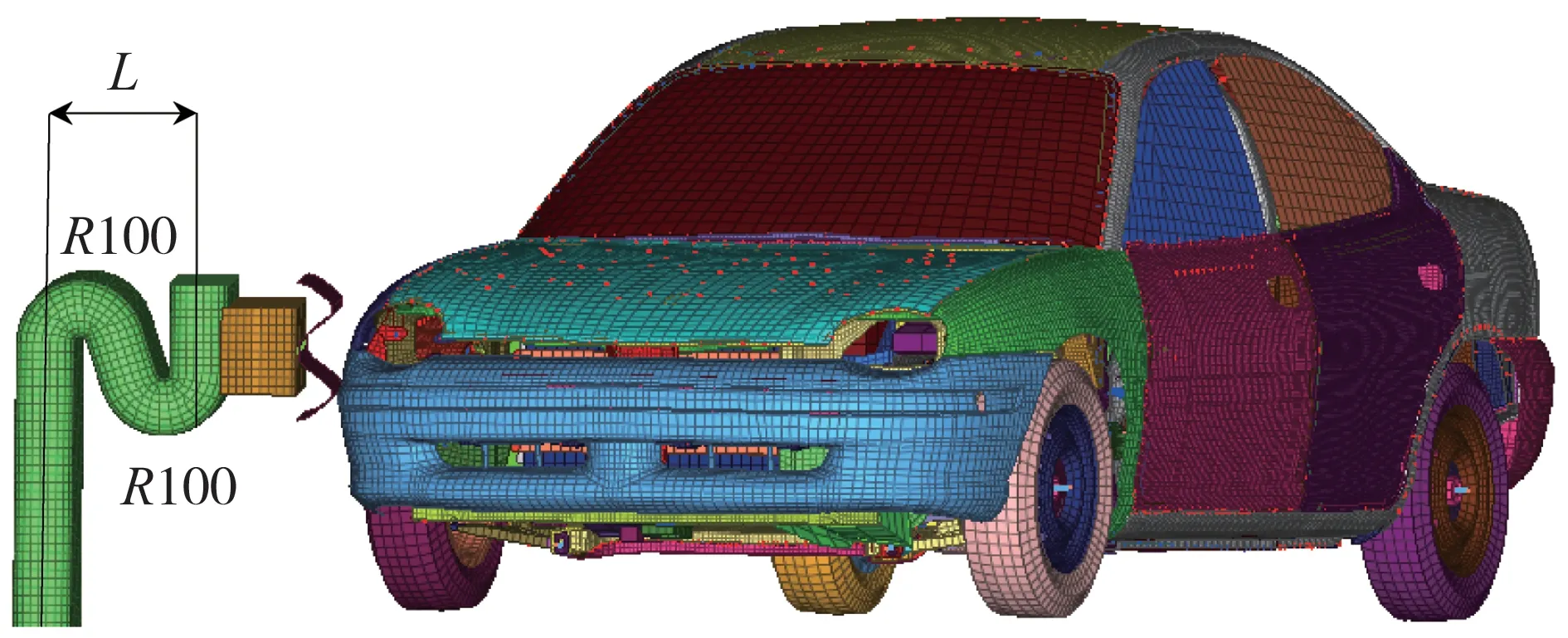
图9 N型弯曲立柱护栏与汽车碰撞仿真模型

N型立柱中心线间距的大小（图9中L）对仿真结果影响较大，通过仿真发现350 mm的间距已能避免绊阻，为确定最佳间距值，又仿真了450和550 mm两个间距，并对3个间距的仿真结果进行比较。结果显示：随着间距的增大，车辆质心处最大加速度由大变小又变大，间距350、450和550 mm对应的车辆质心最大加速度分别为19.3g、15.2g和21.1g，可见间距450 mm最有利于乘员安全。

N型立柱在碰撞过程中的变形情况如图10所示。可以看出，由于立柱与护栏板的横向距离加大，给车轮提供了更大避让空间，使碰撞的激烈程度降低，从而降低了对乘员的伤害。

图10 N型立柱与车辆碰撞变形情况

4 护栏系统优化

全面的护栏系统优化要考虑多种车辆在多种情况下与护栏发生碰撞，但是由于立柱绊阻通常发生于小型车辆撞击护栏，本文基于轿车-护栏碰撞的仿真模型，利用正交试验找出最优参数组合，以提高护栏的防绊阻性能，为护栏的设计提供参考。

4.1 正交试验方案

影响护栏防撞性的因素包括波形梁板、立柱和防阻块。本文主要研究护栏的立柱，而立柱的间距、厚度、直径、埋入混凝土的深度、结构型式等均对汽车-护栏碰撞系统造成影响。立柱的间距对于整个系统的影响非常大，减小立柱的间距可以增强护栏的整体强度；立柱的结构形式，例如填充型和弯曲型的立柱，都有助于提高碰撞安全性；增加护栏各部件的厚度可以提高护栏的强度。本文选取与立柱相关的参数，即立柱的间距、厚度和结构型式，以及梁板的厚度作为影响因素来寻找最优组合。所选影响因素及其取值如表1所示，影响因素均为三水平，为减少试验次数，选择L9（34）正交表，共做9组仿真，以车辆的质心最大加速度和护栏的最大横向变形量作为指标。

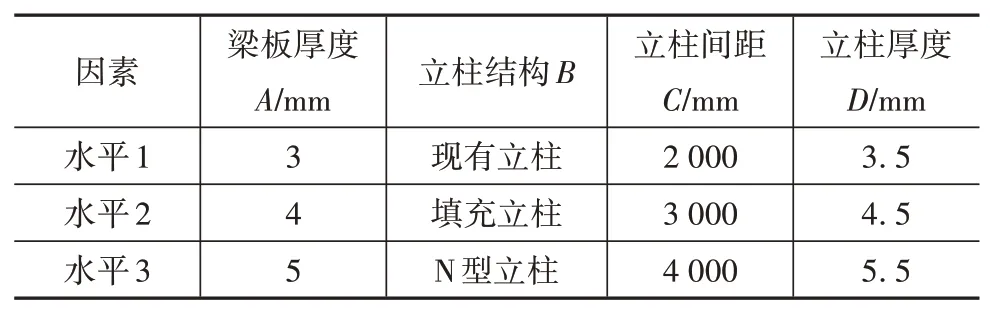
表1 正交试验因素水平表

4.2 参数优化组合

表2 示出两个指标在各项仿真中的数值，其中M1、M2、M3分别为因素所在列对应数字1、2、3的指标值的总和，用来衡量各因素对于指标的影响程度。每个因素的极差R为该因素的M1、M2、M3中的最大值与最小值的差，极差大的因素为主要因素，受水平的影响大。T表示同一因素的M1、M2、M3之和，用来检查M1、M2、M3的计算是否正确。

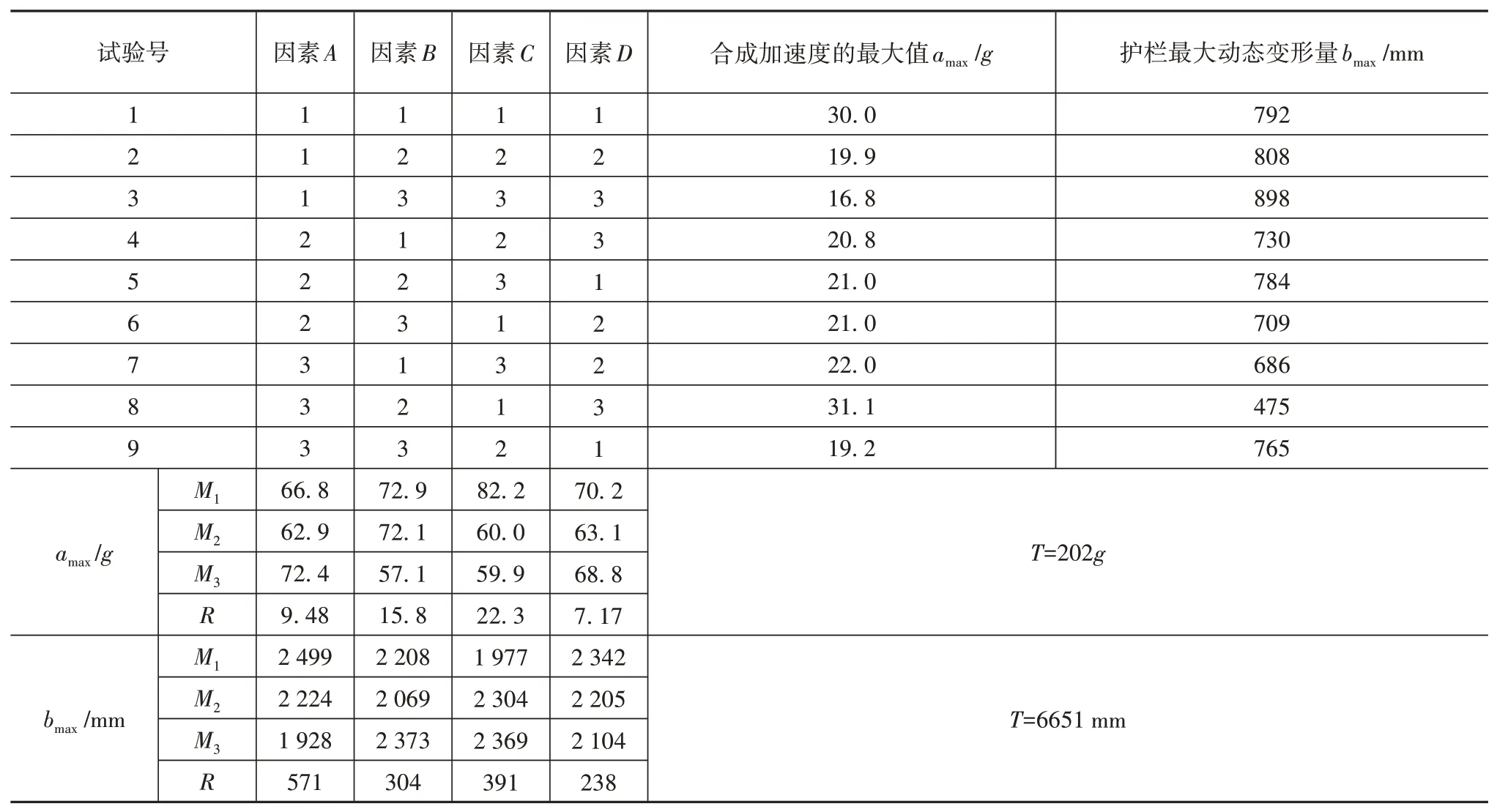
表2 正交试验因素水平组合及计算结果

对比表2的极差R值可以看出，4个因素对车辆质心最大加速度的影响程度为C（立柱间距）＞B（立柱结构）＞A（梁板厚度）＞D（立柱厚度），对护栏最大动态变形量的影响程度为A（梁板厚度）＞C（立柱间距）＞B（立柱结构）＞D（立柱厚度）。

图11 是以各因素的水平数为横坐标、相应的M1、M2、M3为纵坐标绘制的车辆质心最大加速度及护栏最大横向变形量受各因素影响的趋势图。从图中可以看出，这两个指标随因素水平的变化趋势。

这9组仿真的护栏最大横向变形均在标准规定的1 000 mm以内，所以最优组合主要考虑碰撞过程中对于乘员的伤害，即车辆质心最大加速度，按照M33＜M32＜M31可以确定立柱间距的最佳水平为4 000 mm，采用类似的方法可以确定立柱结构的最佳水平为N型弯曲立柱，梁板厚度的最佳水平为4 mm，立柱厚度的最佳水平为4.5 mm。对于护栏最大横向变形，影响最大的因素是梁板厚度，当梁板厚度为5 mm时护栏变形量最小，但是加速度会增高很多，折衷方案选择梁板厚度为4 mm。综合考虑车辆质心最大加速度和护栏横向变形的影响因素，可以确定最优组合为A2B3C3D2，即梁板厚度4 mm，N型弯曲立柱，立柱间距4 000 mm，立柱厚度4.5 mm。

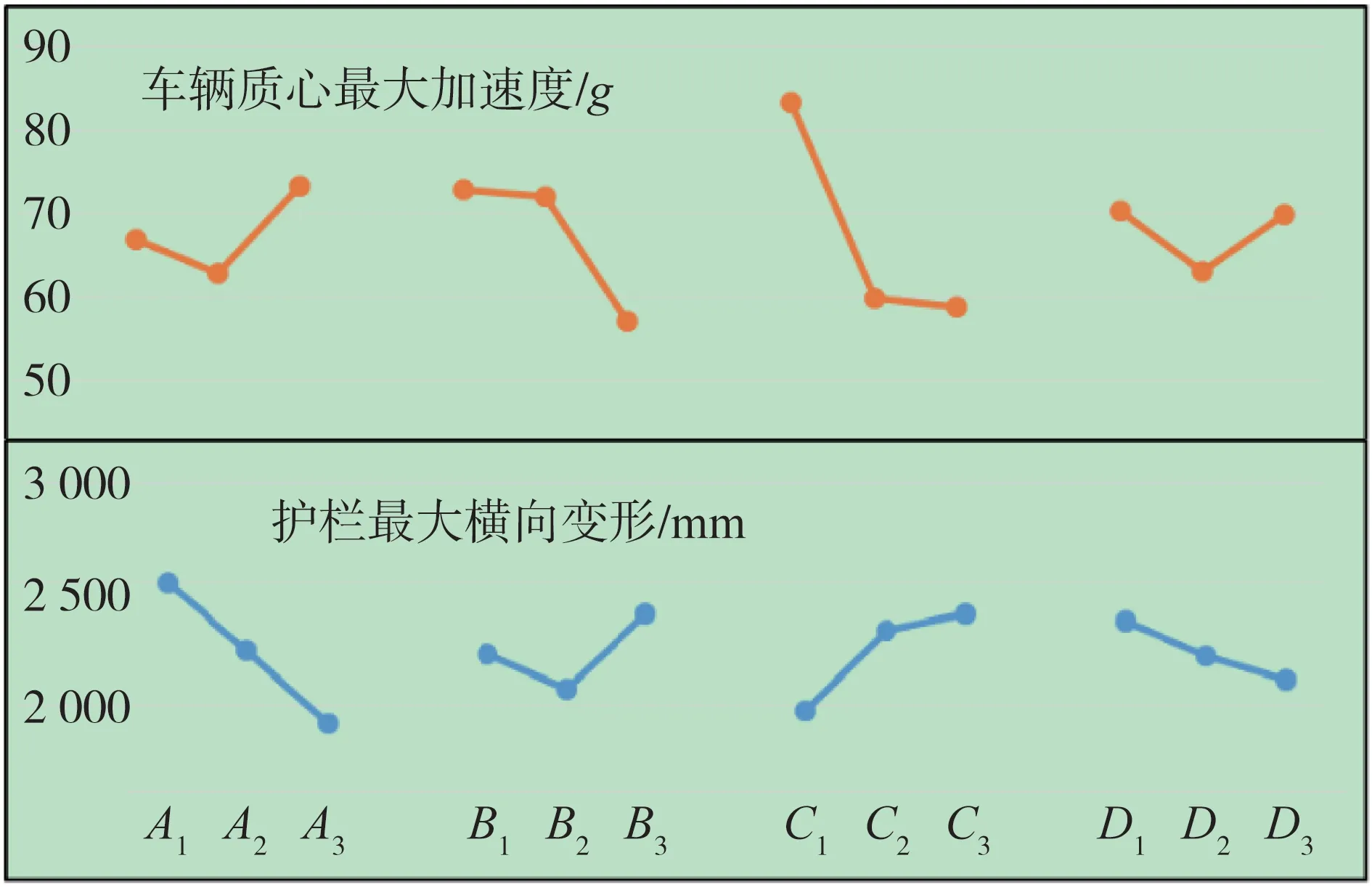
图11 车辆质心最大加速度和护栏最大横向变形量受各因素影响趋势图

4.3 最优组合的验证

通过正交试验推断的最优参数组合A2B3C3D2在正交试验中并没有被安排，需要根据这一组参数建立有限元模型并做仿真分析。仿真结果显示：车辆质心最大加速度为15.2g，比原护栏减小7.9g；吸收78.8%的总体内能，比原护栏提高了2.1百分点；最大横向变形857 mm，比原护栏略高，但未超过规定限值。

为衡量护栏引导车辆的能力，通过增大碰撞角度，加大立柱绊阻的几率，对原护栏和优化护栏进行仿真分析。图12为汽车碰撞原护栏和优化护栏的运动轨迹。由图可以看出，原护栏在碰撞初期能够对车辆进行导向，慢慢修正车辆的运动方向，在100 ms时刻车辆与第1根立柱直接碰撞，立柱与防阻块之间的连接失效，立柱向下倒伏，由于车辆的初始动量较大，顺利通过了第1根立柱，但是在300 ms时刻与第2根立柱发生了严重绊阻，在惯性力作用下绕立柱产生猛烈旋转，右前轮外偏，车辆尾部远离护栏，车体与护栏之间构成较大夹角，并于450 ms时刻仿真终止，车辆未能导出。而优化的护栏能够修正车辆的运动轨迹，将车辆顺利导出，车辆碰撞两根立柱均未发生绊阻。

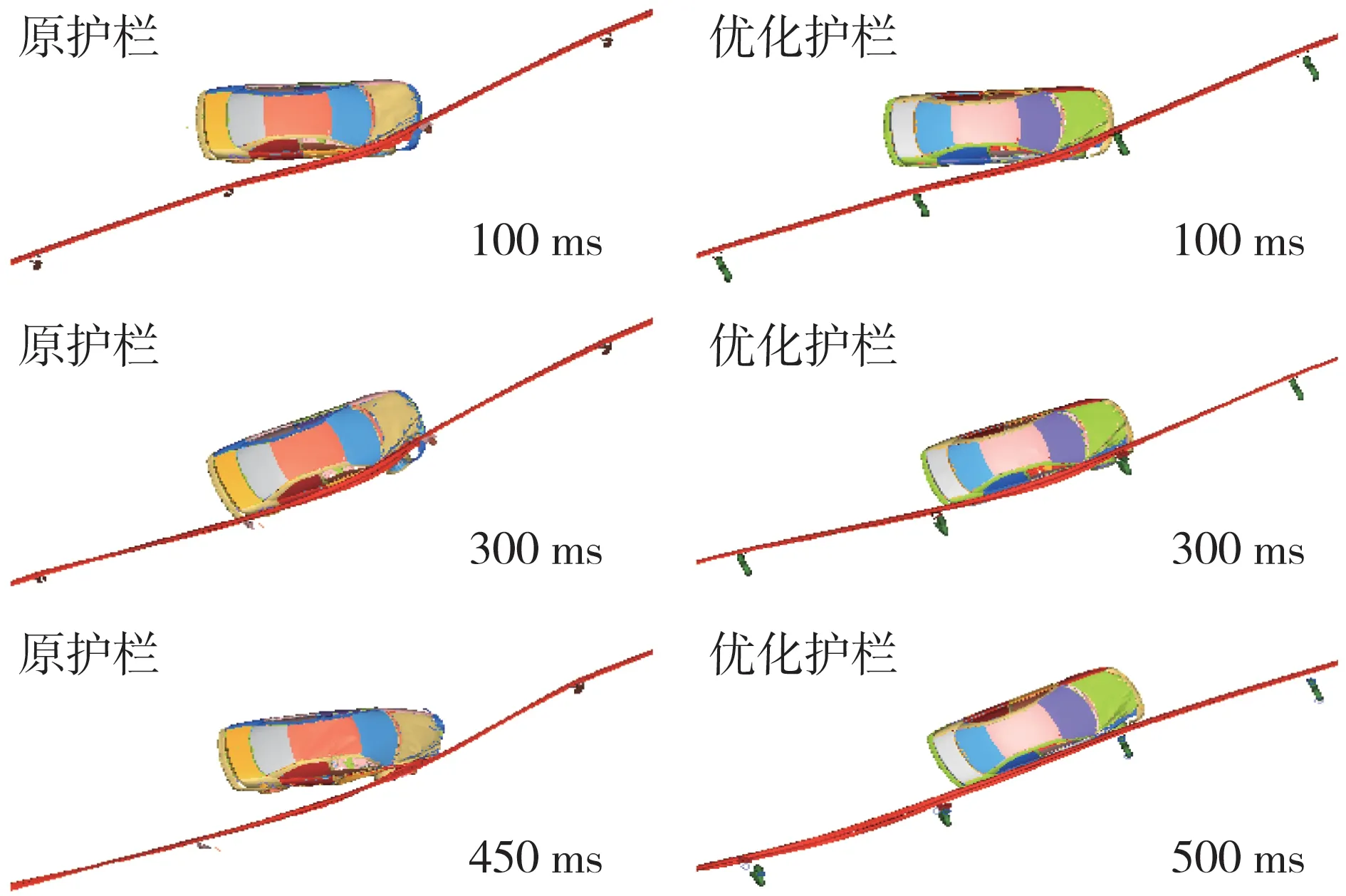
图12 汽车碰撞原护栏和优化护栏的运动轨迹

5 结论

以某轿车与双波型护栏为研究对象，利用HyperWorks和LS-DYNA软件仿真整个碰撞过程。通过分析汽车质心处的合加速度、汽车的运行轨迹以及护栏的最大变形量发现现有护栏的不足，并对立柱进行改进，最后通过正交试验优化了护栏，主要结论如下。

（1）碰撞过程中立柱与车轮会发生绊阻，导致汽车质心处最大加速度值超过国家规定限值，对车辆乘员危害性较大。绊阻与立柱变形关系密切，随着碰撞的持续深入，立柱在地面以下400 mm处形成塑性铰，开始发生塑性变形。当车轮行驶到立柱处，由于碰撞角度及摩擦等因素使立柱置于车轮的内侧，随后车轮逐渐外偏，形成了立柱对车轮的绊阻。

（2）提出了两种防止绊阻的立柱改进方案。第一种是填充型立柱，在空心圆筒立柱中填充聚亚安酯泡沫材料，既能增强立柱提高吸能性，又能对车辆起缓冲作用。第二种是中心线距离为450 mm的N型弯曲立柱，通过改变立柱的结构，增大立柱与梁板的横向距离，从而降低车辆与立柱接触的可能，避免立柱对车轮形成绊阻。

（3）通过正交试验能够发现护栏主要部件参数对车辆质心最大加速度和护栏最大动态变形量的影响规律，从而获得最优参数组合，以有效防止立柱绊阻，顺利将车辆导出。