汽车后副车架轻量化概念设计方法研究*

2021-06-09马芳武王卓君梁鸿宇武振江蒲永锋

汽车工程 2021年5期

马芳武，王卓君，杨猛，梁鸿宇，武振江，蒲永锋

（1.吉林大学，汽车仿真与控制国家重点实验室，长春 130022；2.中汽研（天津）汽车工程研究院有限公司第三开发本部，天津 300300）

前言

在汽车产品概念设计阶段，仅通过少量的设计参数建立结构的CAD模型，结构优化分析时再反复修改CAD模型进行相应的CAE分析，不仅耗费大量时间，而且无法充分利用概念设计阶段较大的设计空间［1］。因此，在概念设计阶段引入结构性能分析，能够缩短开发时间，提高拓扑优化与形状优化的可能性［2］。

在概念设计阶段，根据拓扑优化结果及造型、截面等数据建立参数化模型，并在设计初期进行多学科优化，可以更有针对性地进行汽车产品开发［3］。参数化建模包括显式参数化建模和隐式参数化建模，由于显式参数化建模难以解决零部件的大变形问题以及装配关系的更新，目前学者广泛采用隐式参数化建模技术实现“分析驱动设计”［4-5］。基于隐式参数化模型的优化设计主要针对已有的结构进行改型，均实现了良好的轻量化效果［6-8］。Wang等［9］基于隐式参数化建模对白车身进行轻量化设计，在保证静动态性能的前提下质量减轻了7.63%。Duan等［10］将隐式参数化模型与全局灵敏度分析方法结合对白车身进行轻量化设计，有效地降低了设计复杂度。

虽然隐式参数化建模与多目标优化方法结合已有较好的研究基础，但针对模型中梁截面形状优化的研究较少，且多是对模型中的单个梁进行截面优化设计。桂春阳和左文杰等［11-12］针对梁的冲压工艺约束对截面控制点进行了数学定量描述。梁伟强［13］则采用截面形状控制方法对梁截面进行优化，为结构概念设计提供参考。基于此，本文中提出在概念设计阶段结合隐式参数化建模与截面形状控制方法对后副车架整体进行轻量化优化设计。

本文中首先对后副车架设计空间进行综合目标拓扑优化，得到了结构的传力路径。采用SFE⁃Concept软件，综合考虑零部件的位置、结构、形状进行隐式参数化建模。在满足后副车架目标性能的条件下，结合截面形状控制方法以零件位置、形状、尺寸、材料等为设计变量，对建立的隐式参数化模型进行结构-材料-性能一体化优化设计，从而减轻结构质量。

1 后副车架综合目标拓扑优化

在汽车零部件的概念设计阶段，拓扑优化使工程师不再局限于传统的结构形式，为产品的更新与开发提供了新的设计思路，从而有效地提高了结构的轻量化潜力。

1.1 拓扑优化模型的建立

拓扑优化设计结果在一定程度上会受到模型的影响，因此在建立设计空间时需遵循一定的设计规范，在最大化设计空间的同时避免与相邻零部件发生运动干涉。建立的后副车架拓扑优化模型如图1所示。综合考虑计算效率及结果精度，本文中采用平均尺寸为5 mm的六面体单元对后副车架初始模型进行网格划分。后副车架材料参数如表1所示。

为使拓扑优化结果更具指导意义，对设计区域进行分组，便于后期对零件材料进行参数化。根据制造工艺条件设置不同方向的拔模约束，并施加最大、最小成员尺寸约束保证结构的均匀性和可加工性。

图1 后副车架拓扑优化模型

表1 后副车架材料属性

1.2 基于折衷规划法的多目标优化模型

本文中对后副车架进行6种典型工况的研究，每个不同的载荷工况必将得到不同的拓扑优化结果，因此其本质上属于多目标优化问题［14-15］。本文中采用折衷规划法将多目标优化转换为单目标优化问题。

为获得具有良好性能的副车架结构，以结构刚度最大化为目标，在实际研究中将其转化为柔度最小问题，即结构单元总应变能最小。结合折衷规划法可得多工况拓扑优化目标函数为

式中：ρ为材料密度；m为载荷工况总数，本文中m=6；w k为第k个工况的权重系数；q为惩罚因子且q≥2，本文中取q=2；C k(ρ)为第k个载荷工况的单元总应变能函数为第k个载荷工况结构的总应变能函数的最大值为第k个载荷工况结构的总应变能函数的最小值；V(ρ)为优化后结构的有效体积；V0为结构的原始体积；f为体积约束的百分比，本文中取f=0.2；σk为第k个载荷工况的最大应力值；[σ]为材料的许用应力。

在结构的多工况优化设计过程中，各工况权重值的选择一直是研究的热点问题［16］。然而，现阶段对汽车典型极限工况的使用频率并没有针对性研究，且不同类型的汽车设计要求差异，因此每种工况的设计权重也不同。根据文献和设计经验综合考虑各工况权重值设定［17］，如表2所示。

表2 后副车架典型极限工况的权重设置

1.3 拓扑优化结果与分析

经过155次迭代，得到最终拓扑优化结果，如图2所示。采用折衷规划法进行的多工况拓扑优化使结构材料分布特征明显，因此该结果可为后续几何模型转化提供参考。为在概念设计阶段提高产品设计效率.增加结构的优化设计空间，合理的建模方法及参数化优化方法也尤为重要。

图2 后副车架拓扑优化结果

2 后副车架隐式参数化建模

隐式参数化建模采用数学描述对结构模型进行建立和修改，通过基本参数化元素即基点、基线和基本截面生成高级参数化元素即梁结构、连接接头、自由曲面等，零部件间的连接关系通过数学映射的方法建立，因此通过改变基本参数化元素就可以满足结构形状变化的要求。隐式参数化建模映射连接关系稳定、能够自动划分有限元网格，便于进行封闭式集成优化。当结构复杂，零部件较多时，控制零件形状的局部截面随之增多，因此在进行隐式参数化建模的过程中需要避免设计变量之间的耦合现象。

2.1 后副车架隐式参数化模型的建立

分析图2所示拓扑优化结果可知，后副车架前后横梁及侧梁位置均为空心结构，因此选择板壳冲压式结构为骨架。在进行整体结构划分时需综合考虑拓扑优化结果、参考车型后副车架结构和制造装配要求。为便于后续设计变量的选取，在零件形状发生变化的位置、零件间连接位置等处分别插入局部截面；同一零件上相邻局部截面的控制点位置避免发生较大变化；基点、基线的位置尽量在该零件设计空间的边界处。综上所述，建立的后副车架隐式参数化模型如图3所示。

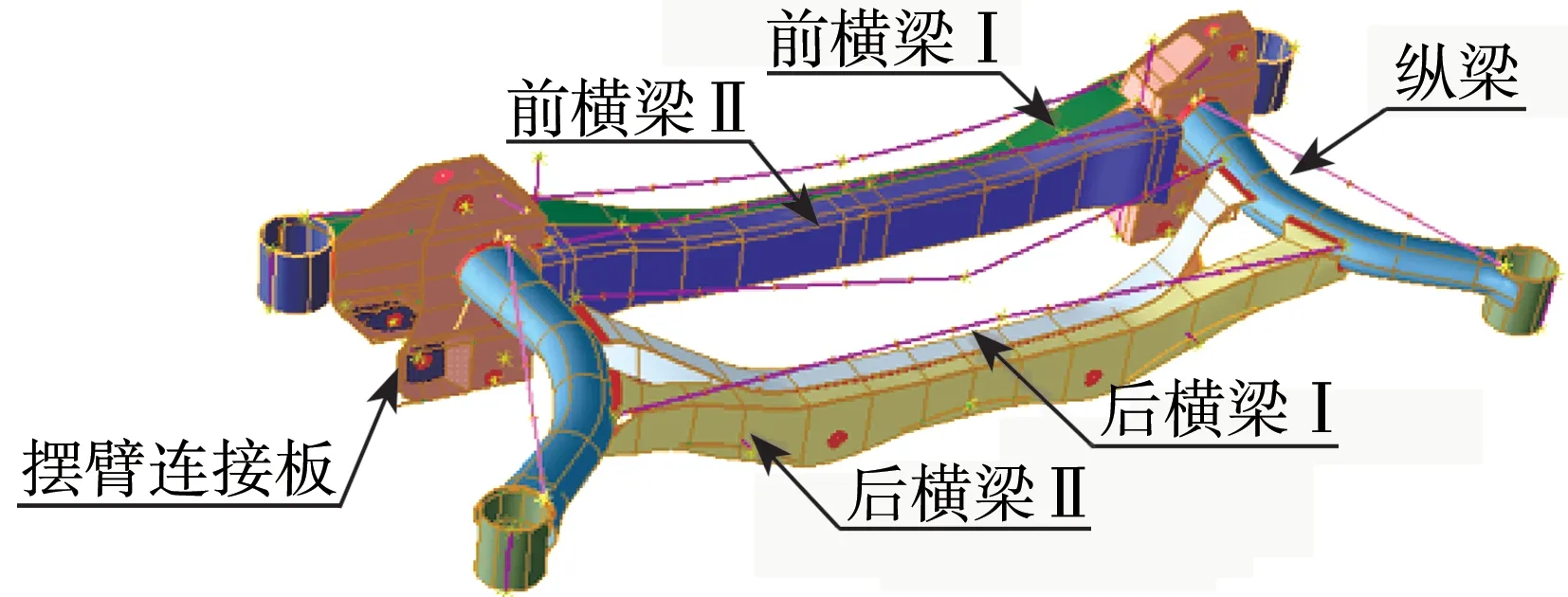
图3 后副车架隐式参数化模型

2.2 后副车架隐式参数化模型的性能分析

为保证后续用于优化设计的模型具有可靠性，需对2.1节中建立的隐式参数化模型进行性能分析，下面将从强度、刚度和自由模态3方面进行仿真分析。

2.2.1 强度分析

根据该汽车后副车架的实际受力状况，分析在上述6种典型极限工况下结构的最大应力，分别为504、150、385、216、274和493 MPa，低于材料的屈服强度550 MPa。

2.2.2 硬点静态刚度分析

后副车架与车身连接位置处进行全自由度约束，分别对各硬点进行X、Y、Z方向1 000 N的加载，各硬点刚度值如表3所示。

根据仿真结果可知，各硬点刚度值均满足使用要求，该结构仍具有优化设计空间。

表3 后副车架参数化模型的各硬点刚度值

2.2.3 自由模态分析

自由模态是在不考虑约束条件时的副车架固有振动特性［18］，仿真提取前3阶非刚体自由模态，如表4所示。各阶自由模态频率均满足结构设计目标值。

根据上述分析可知，建立的隐式参数化模型性能均满足目标值，该结构仍具有优化设计空间，将利用此模型进行后续的结构优化设计。

表4 后副车架参数化模型的固有频率

3 后副车架结构优化设计

在对参数化后副车架进行结构优化设计时，首先对模型进行设计变量的选取，结合试验设计方法生成设计矩阵，循环执行求解器进行分析计算。为提高优化设计效率，采用数学模型构造性能响应与设计变量之间的关系，结合优化算法对后副车架进行结构优化设计并进行性能仿真验证。

3.1 确定结构设计变量

3.1.1 零件形状设计变量

常用的截面形状控制方法有偏置法、矩形模拟法、扁宽截面法、极坐标法和比例向量法［19］。相对于其他方法，比例向量法控制变量少，能够在已有的截面形状基础上生成新的截面形状，不受初始形状的约束。比例向量法通过引入一个固定的角度值θ和一个变化的度量值SV实现截面形状的连续变化，在复杂情况下也可将角度值作为设计变量。比例向量法截面形状控制示意图如图4所示，其中点12'、13'、14'为节点12、13、14经比例向量法坐标变换后的位置。

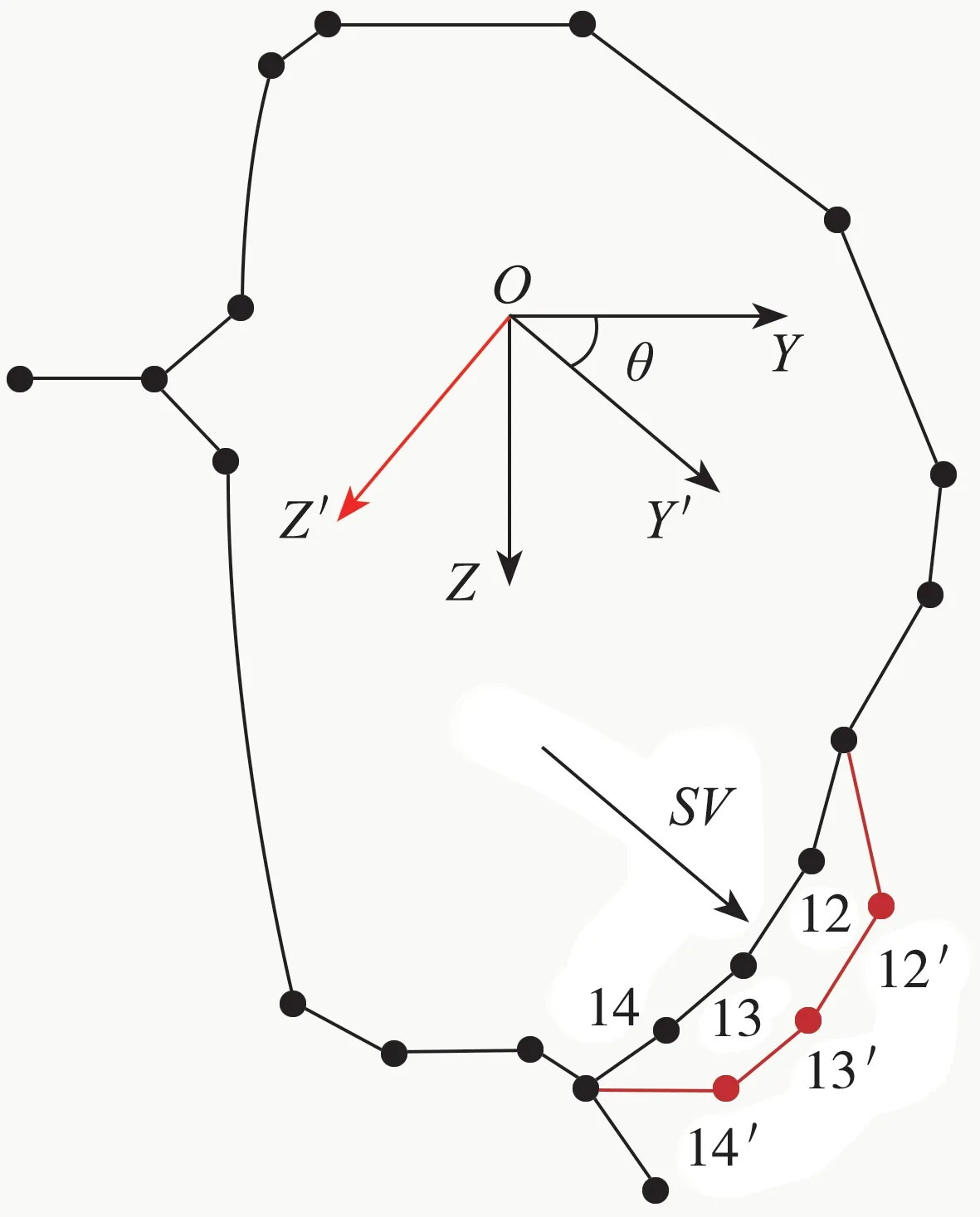
图4 比例向量法截面形状控制示意图

初始坐标系YOZ经某一固定角度旋转后得新坐标系Y'O Z'，再对其中节点坐标进行以度量值为SV的缩放，某个初始点坐标为P(y，z)，变换为R(y'，z')，坐标变换公式为

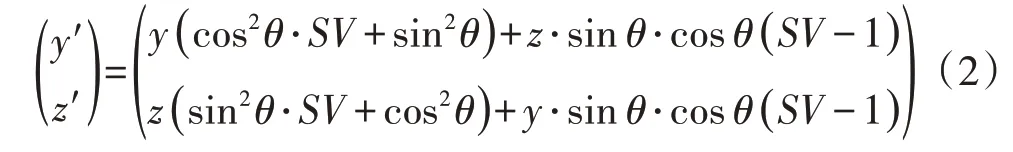
当角度值θ=0°时，控制点坐标沿Y轴以度量值S V进行缩放；当角度值θ=90°时，控制点坐标沿Z轴以度量值SV进行缩放。

后副车架纵梁结构的比例缩放如图5所示。其中，将度量值进行参数化。考虑到零件间连接位置的稳定性以及形状的一致性，对纵梁中间的4个局部截面分别进行沿Y轴、Z轴的缩放控制。

图5 角度值θ=0°，度量值SV=1.2，沿坐标系Y轴缩放梁模型示意图

对后副车架的横梁结构进行形状变化控制点的选取，如图6所示。

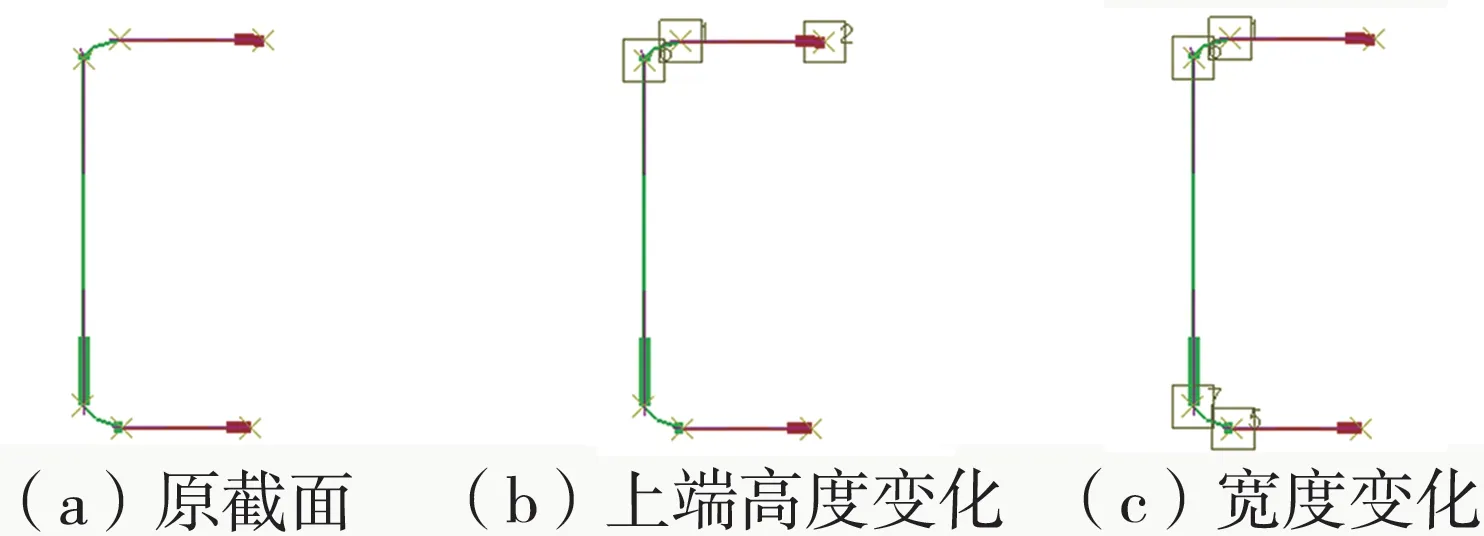
图6 横梁形状控制点选取

选取零件的局部截面形状变量18个，以及前、后横梁及纵梁的曲率变量3个，该变量采用移动梁结构单个基点位置的方法进行实现。

3.1.2 零件位置设计变量

对零件位置进行参数化时，选择梁结构的基点进行整体移动，当零件位置变化时连接关系将自动得到调整，无须重新建立。本文中对后横梁及结构加强板的4个位置变量进行了参数化。

3.1.3 零件尺寸及材料设计变量

对零件的厚度尺寸进行参数化，共计10个设计变量。由于纵梁在极限工况下受力较小，将该部分用牌号为6061的铝合金代替后的拓扑优化结果形式与钢材类似，因此将其材料进行参数化为1个设计变量。

综上所述，共计36个设计变量，如表5~表8所示。设计变量零件位置如图7~图10所示。

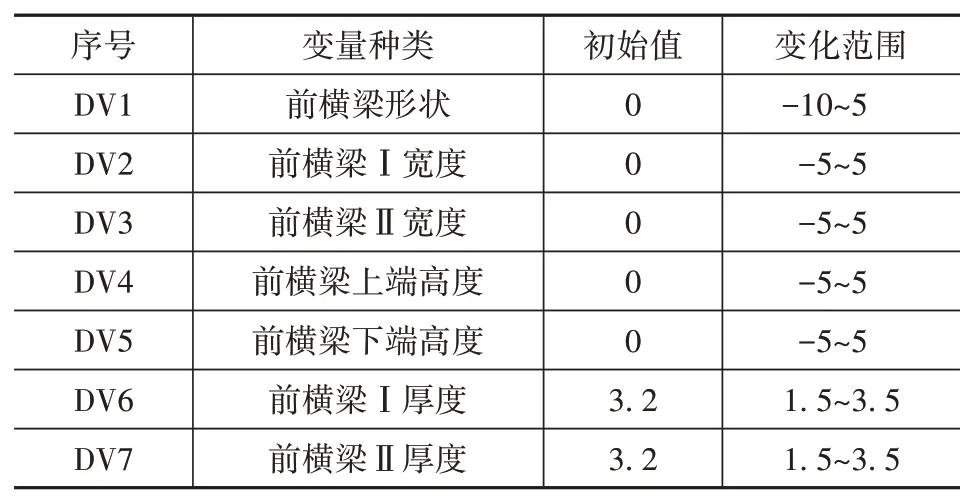
表5 前横梁设计变量表 mm

表6 摆臂连接板设计变量表 mm

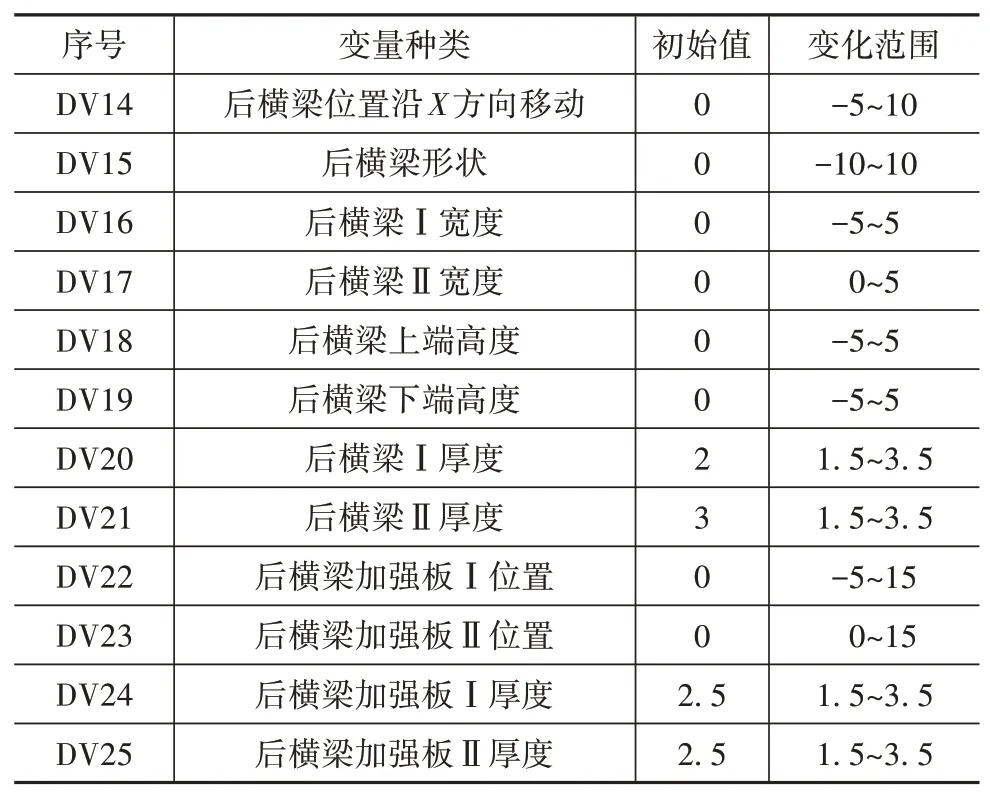
表7 后横梁设计变量表 mm

表8 纵梁设计变量表

图7 前横梁设计变量示意图

图8 摆臂连接板设计变量示意图

图9 后横梁设计变量示意图

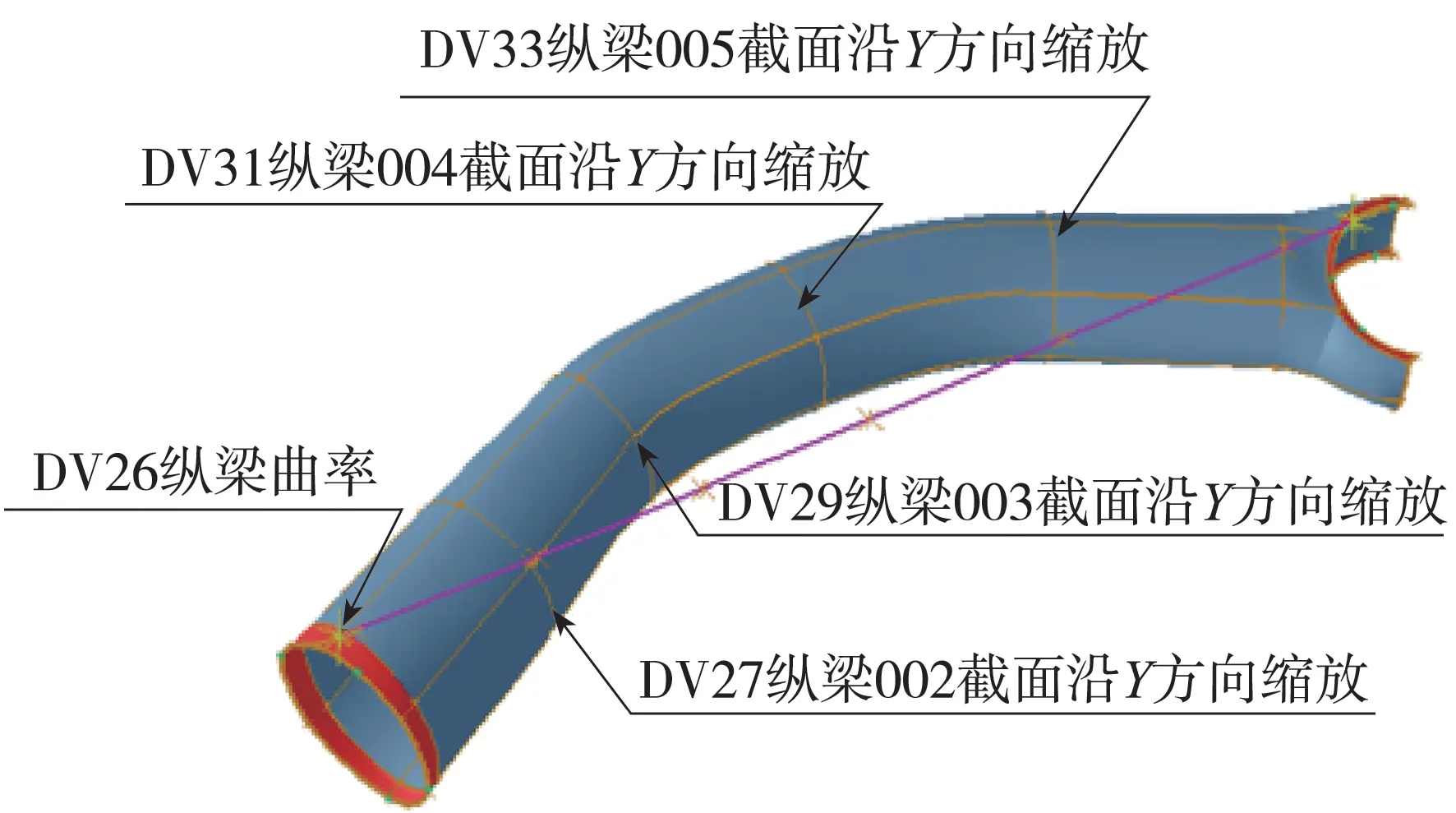
图10 纵梁设计变量示意图

3.2 结构优化设计

针对后副车架的形状、位置和材料的性能响应具有较强的非线性，因此选择最优拉丁超立方设计，该方法能均匀填充设计空间［20］，在拟合非线性响应方面具有优势。椭圆基（EBF）神经网络模型具有较强的拟合复杂非线性函数的能力。选择在多目标优化中具有较好收敛能力的第二代遗传算法［21］结合椭圆基神经网络模型进行优化设计。

对后副车架进行概念设计阶段的结构优化设计时，需考虑结构的强度、硬点刚度及模态频率，以结构质量最小、第1阶模态频率最大为目标，约束结构的硬点刚度和第2、3阶模态频率，优化设计的数学模型如下。

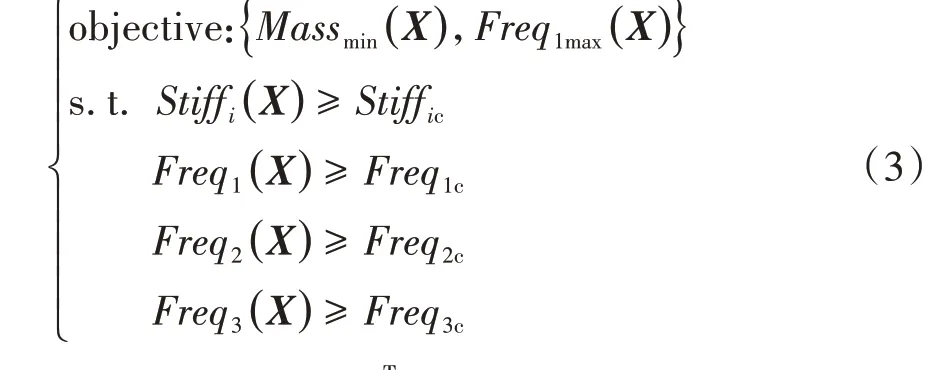
式中：X={x1，x2，…x n}T为n个设计变量，Mas smin(X)为后副车架最小质量；Fr e q1max(X)为后副车架第1阶固有频率最大值；S tiff i(X)为副车架第i个硬点刚度；Stiff ic为副车架第i个硬点刚度的设计指标；Fr eq1(X)、Fre q2(X)、Freq3(X)分别为后副车架的第1阶、第2阶、第3阶固有频率；Freq1c、Freq2c、Freq3c为后副车架第1阶、第2阶、第3阶固有频率设计指标。

后副车架结构优化设计的流程如图11所示。图中，“SFE⁃Concept”为模型参数化模块，“PROP”为尺寸和材料参数化模块，“MASS”为质量计算模块，“MODE”为模态提取模块，“STIFFNESS Calculator”为硬点刚度分析模块，“rename”模块用于对结果分析文件重命名。对试验结果进行拟合后需对代理模型精度进行检验，满足条件后进行多目标优化设计，如图12所示。

图11 后副车架结构优化流程

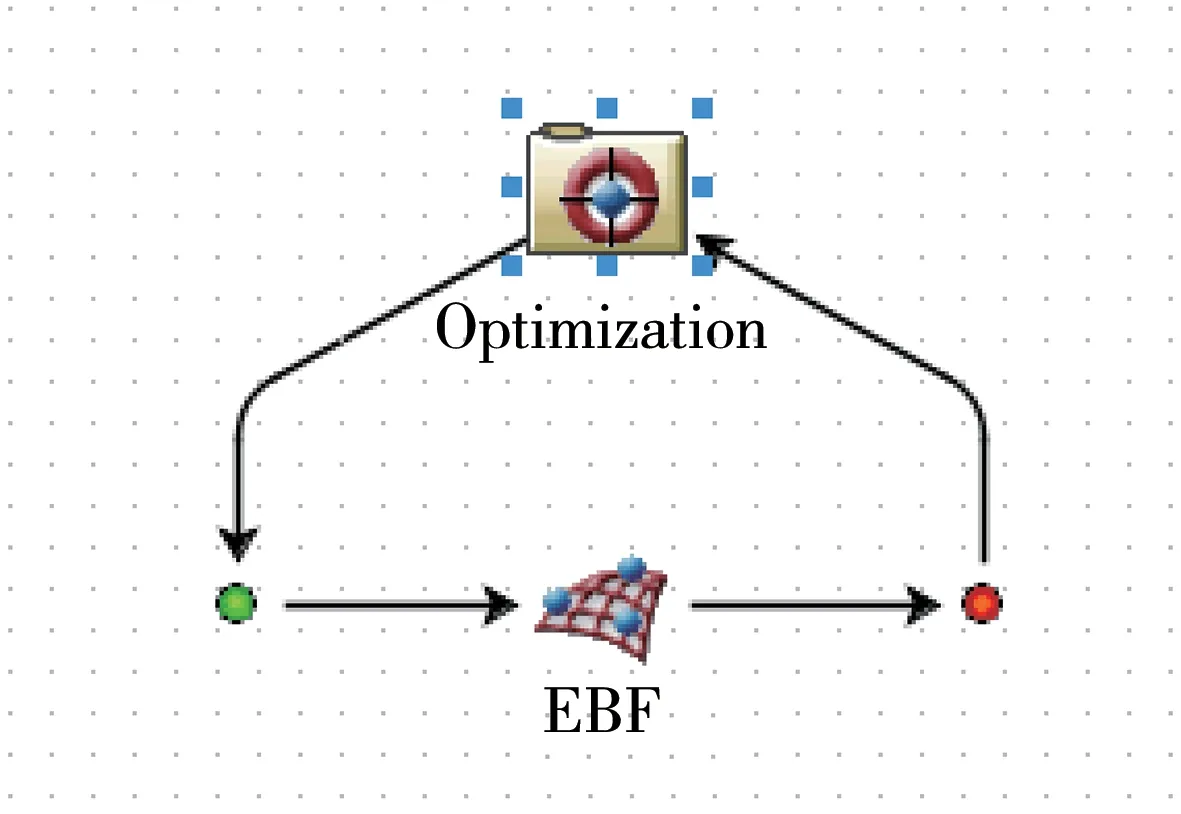
图12 多目标优化设计流程

3.3 后副车架结构优化性能对比

采用交叉验证的方式检验代理模型的精确度，决定系数R2均大于0.9，可以使用代理模型的方法进行优化设计，设置种群数目为200，迭代数目为300进行多目标优化设计，选取后副车架质量最低的妥协解作为优化解。初始模型质量为16.6 kg，优化后模型质量为14.19 kg，减轻14.5%。进一步分析检验优化结果的强度性能，并对硬点刚度与模态进行验证。

3.3.1 强度分析

验证在上述6种典型极限工况下结构的最大应力，边界条件同2.2.1节，各工况下结构最大应力分别为528、225、405、302、331和536 MPa，低于材料的屈服强度550 MPa。

3.3.2 硬点静态刚度分析

对结构优化后的后副车架进行硬点静态刚度分析，载荷边界条件同2.2.2节，经仿真分析结果如表9所示。

结构优化后的后副车架各硬点刚度均满足设计指标。

3.3.3 自由模态分析

对结构优化后的后副车架进行自由模态分析，固有频率如表10所示。

结构优化后的前3阶固有频率均满足设计指标。