基于电池寿命预测控制的履带车辆能量管理*

韩立金，刘 辉，刘 聪，刘宝帅，张 聪

（1.北京理工大学机械与车辆学院，北京 100081；2.北京理工大学前沿技术研究院，济南 250307）

前言

目前，新能源车辆主要有纯电动车辆（electric vehicle，EV），混合动力车辆（hybrid electric vehicle，HEV）和燃料电池车辆（fuel cell vehicle）3种［1］。但由于现阶段电池的比能量相对较小，而车载空间有限，使得纯电动车辆拥有续驶里程不足等问题［2］。尤其对履带车辆而言，车质量较大且行驶工况复杂，所需的电功率很大，当前还不能实现完全由电池驱动。此外，燃料电池车辆燃料不宜存储，因此借助混合动力系统提高整车经济性和续驶里程是一种较好的选择。

能量管理策略主要依据拥有较多设计经验的工程师驾驶员的驾驶习惯、试验数据、车辆参数和性能要求等进行设计［3］。Biasini等以中型混合动力货车为研究对象，提取出一种近似最优的基于规则的能量管理策略用以分配需求功率，以达到降低油耗和维持电池SOC稳定的目的［4］；Hemi等建立了整车的模糊规则控制器以对发动机和电池的目标功率进行分配，提高了控制策略的适用范围［5］；基于规则的能量管理策略一方面设计难度加大，另一方面其控制效果也不能得到保证。为进一步提高控制器的控制效果并解决在一定的约束条件下的多目标优化问题，很多研究机构在基于优化能量管理策略上进行了探索［6-7］。Zhang等提出了一种基于动态规划的最优能量管理策略，并考虑到电池的健康状态以及SOC的影响［8］；Van等给出了一种针对标量状态约束最优控制问题的数值求解方法，在混合动力车辆系统中可用于预定义功率和车速的轨迹［9］。Zheng等针对燃料电池混合动力车辆，采用极小值原理离线优化了车速的分布，并使得燃油消耗率最小［10］。Wang等针对串联式混合动力履带式推土机提出了一种基于MPC的能量管理策略，并借助履带式推土机的典型工况进行MPC策略的开发［11］。近年来，随着智能控制算法的进一步发展和完善，很多学者期望通过智能控制算法来寻求最优控制问题的解，从而设计混合动力能量管理策略［12-13］。Wu等提出了一种基于学习矢量量化算法的驾驶循环识别方法，利用粒子群算法优化不同驾驶循环下隶属度函数和规则，从而提高并联混合动力汽车的燃油经济性［14］。Deng等提出一种新型的混沌遗传算法，优化了模糊能量管理策略中的隶属度函数与模糊规则［15］。

以上方法都能表现出较好的燃油经济性，然而大多数研究方法仅适用于单一理想工况下，并且针对极限行驶工况中电池保护的效果欠佳。此外，智能算法求解过程较复杂，很难满足系统的实时性要求。面对以上问题，本文中针对战场中串联式混合动力履带车辆，设计了一种基于非线性模型预测控制的能量管理策略。建立了基于电池寿命的非线性预测控制模型，在每一采样时刻对预测时域内的需求功率进行分配。同时，提出了从减少优化变量和缩小搜索域两个方面提高求解速度，最后通过仿真及硬件在环实验验证了所提出策略的有效性和实时性。

1 串联式混合动力履带车辆关键系统建模

1.1 动力系统整体结构布局

本文的研究对象为带耦合机构的串联式混合动力履带车辆，其传动系统主要由发动机发电机组、电池、电机和机械传动组成，传动系统方案如图1所示。考虑到本文的主要研究目的、模型的精度及其运算速度，发动机及电机的模型采用基于数据的建模方法，电池模型采用基于机理的热电耦合模型进行建立，以得到较为准确的电功率响应特性，并考虑温度对电池寿命、内阻和电压等参数的影响。

图1 串联式混合动力车辆传动系统

1.2 电池热电耦合模型

1.2.1 电池2阶RC模型

目前，常见的等效电路模型包括Rint模型、1阶RC模型、2阶RC模型和PNGV模型4种。其中，2阶RC模型具有更高的电压辨识精度，且模型较为简单，因此本文选择2阶RC模型作为串联式混合动力履带车辆的电池模型，如图2所示。

图2 2阶RC模型

电池单体开路电压的取值由SOC和电池温度拟合得到，这里参考了文献［16］中的数据及拟合方法，对于单体电池而言，开路电压值E与SOC的关系式可表述为

式中b3、b2、b1、b0与电池温度相关。

电池两端电压U为

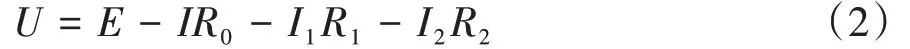
式中：R0为电池内阻；R1、R2分别为电池模型中两个RC网络的电阻值；I1、I2分别为流经电阻R1与R2处电流。

1.2.2 电池热模型

假设电池产生的热量在电池组内均匀分布，Fathabadi等［17］通过研究得出了单位体积电池产热量的计算公式，即

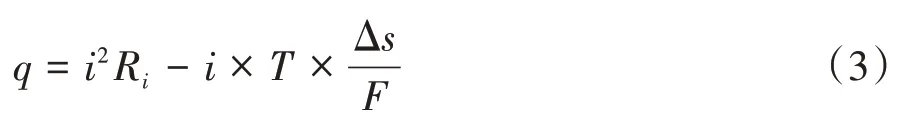
式中：q为单位体积电池组内部产生的热量；R1为电池系统的等效电阻；i为单位体积的放电电流；Δs为电池组的熵变。本文中主要考虑电池温度对电池电阻、寿命等参数的影响，则电池温度为

式中：Tb为电池温度；Te为环境温度，即初始时刻电池的温度值；Q0为初始时刻到当前时刻电池所产生的总热量；Q0为初始时刻到当前时刻电池所放出的总热量；c为电池组的比热容；mbatt为电池组的总质量。

1.2.3 电池寿命模型

一般使用SOH（sate of health）来表示电池的健康状态，它是指电池在一定放电倍率下能够放出的最大电量与电池的额定容量之间的百分比，可由下式表示：

式中：Cres为电池当前状态下充满电时的容量；Ce为电池的额定容量。

由实验数据通过曲线拟合得到不同放电倍率下电池寿命与循环次数的函数关系，拟合函数取二次函数：

式中P1、P2、P3与放电倍率有关。

Arrhenius方程可以表示温度应力对加速产品失效的影响系数，常用于电池的寿命模型中。依据Arrhenius方程式可知，温度对电池寿命产生的加速系数为

式中：Tacc为温度对电池寿命衰减的加速影响因子；Ea为电池的活化能，对于性质相同的电池，活化能Ea可看作常数处理；R为摩尔气体常数；T为电池温度；Tref为参考温度值。

电池SOH的损失计算公式为

式中：f（i，SO H）为考虑电池充放电倍率和当前SOH的影响时，每循环次数下电池寿命的损失值；n为以当前电流i进行充放电一段时间时所对应的电池等效循环次数。

1.3 耦合机构模型

本文中传动系统的耦合机构是由两个行星排互相连接得到的，行星排中齿圈、行星架和太阳轮之间的转速满足以下关系：

式中：ws、wr、wc分别为太阳轮、齿圈和行星架的角速度；k为行星排的固有参数。

对于带耦合机构的传动系统而言，其输入的参数为电机A、B的转速和转矩，输出参数为左右两侧主动轮的转速和转矩值，由耦合机构的具体结构，通过理论计算可得：

式中：Tl、Tr、TA、TB、wl、wr、wA、wB分别为左右两侧主动轮和电机A、B的输出转矩与转速；k为耦合机构所用行星排的参数；kc为侧传动比；i为变速器传动比；JA、JB分别为传动系统等效到电机输出轴处的转动惯量。

2 基于非线性模型预测控制的能量管理策略

非线性模型预测控制是一种基于非线性模型的闭环优化控制策略，是一种在线滚动的优化算法。本文中针对履带车辆行驶环境的特点，以非线性模型预测控制理论为基础，提出了一种适用于串联式混合动力履带车辆的能量管理策略，其整体架构如图3所示。

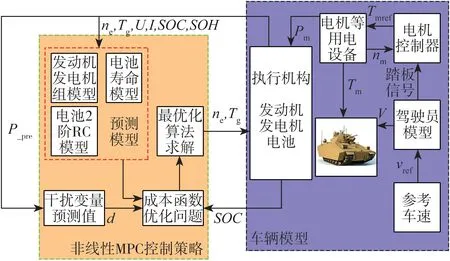
图3 整车能量管理策略框图

2.1 预测模型的建立

考虑电池内阻引起的较快的动态特性，得到系统的电池模型如下：

式中：U0为当前采样时刻的母线电压；I0为电池当前的充放电电流；r为电池的内阻值，不包含两个RC网络的阻值；Pb为电池的充放电功率；C为电池的额定容量。由系统先后功率链功率平衡得：

式中：Pneed为车辆后功率链的需求功率；Tgen为发电机的输入转矩；we为发动机的转速；ηgen为发电机的效率；kgen与发电机的状态有关，发电状态下，其取值为1，电动状态下时，取为-1。

系统的预测模型为

其中：

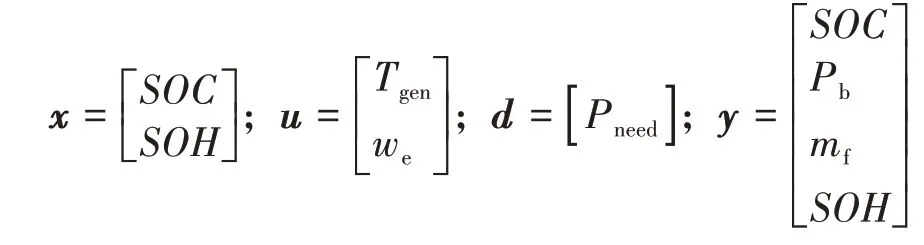
约束条件：

式中：x为系统的状态变量；ΔTgen为发电机的输入转矩的变化量；mf为发动机的燃油消耗；u为系统的控制量；d为系统的干扰变量；y为系统的输出变量。

2.2 不同工况下的成本函数的构建

在串联式混合动力履带车辆复杂行驶环境中，针对不同的行驶工况需求，成本函数的设计需要能够反映出所需优化的目标。因此，本文针对高速良好路面工况，越野行驶工况和电磁炮使用工况设计了一种多层成本函数。

2.2.1 良好高速路面工况下的成本函数

对于良好路面循环工况，目标函数需要平衡燃油经济性与电池寿命之间的矛盾，同时还要兼顾母线电压的稳定性问题，其成本函数可表示为

式中：λsoh、λn、λt、λp分别为权重系数；ṁf_total(t)为总燃油消耗率；dSOH为电池SOH的变化量；Δwe（t）为发动机目标转速的变化量；ΔTgen（t）为发电机目标转矩的变化量；Pb为电池充放电功率；Pb_ref为电池的目标充放电功率。

2.2.2 越野工况下的成本函数

对于越野工况而言，履带车辆的需求功率经常会发生突变，此时后功率链的突然变化的功率需求则完全由电池承担。为减少电池大功率放电的次数，避免导致母线电压低于临界值，还需要考虑电池的储备功率，储备功率的大小由输出功率与电池的最大放电功率之差计算得到，其成本函数可表示为

式中：λd为电池储备功率对应的权重系数；Pbmax为期望的电池最大输出功率，本文中取为200 kW。

2.2.3 电磁炮使用工况下的成本函数

在电磁炮使用工况下，由于电磁炮需求功率大且是突变的形式，因此需要在使用电磁炮前对电池充电，以提高发动机发电机组的输出功率，降低电磁炮使用时对电池放电功率的需求，使母线电压维持在一定范围内。在预测时域内，越野工况下的性能成本函数如下：

式中：Pbn为电池组的期望输出功率；λn为相对应的权重系数。

2.3 障碍函数内点法求解

为便于分析，可将以上建立的非线性优化问题改写为一般形式。此外，通过引入松弛变量l、u使得原问题变为以下优化问题：式中：μ为扰动因子，且满足μ＞0；r为原问题中不等式约束的个数。

经过上述变换得到新的优化问题，其拉格朗日函数如下：

式中：y=［y1，…，y m］，z=［z1，…，z r］，w=［w1，…，w r］为等式约束系数，即拉格朗日乘子，m为原优化问题中等式约束的个数。

当目标函数存在极小值时，拉格朗日函数对所有变量及乘子的偏导数均为0，同时进行线性化处理，得到的矩阵方程为

通过计算上述方程，可以求得下一次迭代的修正量，由此可求出未来时刻的新变量：

2.4 优化问题求解算法的改进

基于内点法的基本原理，为提高优化算法的求解速度，本文可通过减少优化变量和缩小变量的搜索范围两种办法实现。发动机最优转速仅在功率为某些值时变化较快，在其他部分维持不变或缓慢增加，因此仅需对变化较快的部分进行优化即可，优化目的是寻找最优的直线取代转速突变点附近的最优经济曲线，优化变量为直线的斜率及位置，优化的目标函数如下：式中；k为直线的斜率；ξn为斜率相对于油耗的权重系数；ne（x）为不同过渡直线下功率为x时刻发动机的转速，与优化变量有关；P0为转速突变前一点的功率值；n为正整数。n满足：

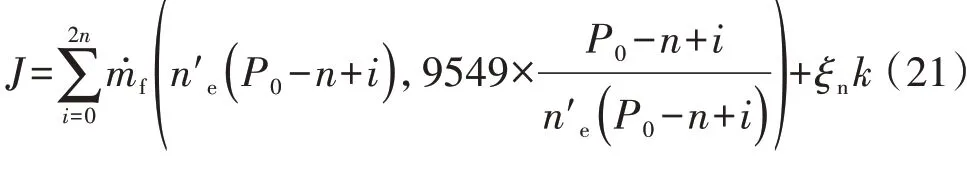
式中：Δne为最优经济曲线上转速突变点处发动机转速的变化量；kmin为要优化的最小斜率值。

当发动机的工作点保持在一条经济曲线上时，发动机的目标转速便与需求功率一一对应起来了，此时的优化变量为发动机的输出功率。当输出功率变化过快时，发动机发电机组也无法实现跟随，同时还可能造成发动机熄火或系统的不稳定，发动机此时的工作点可以被称为不合理工作点，因此本文可通过剔除不合理工作点缩小优化变量的搜索域，以减少计算量。

3 能量管理策略仿真分析与硬件在环试验

3.1 整车能量管理策略仿真试验

3.1.1 良好路面高速工况

从图4和图5可以看出，实际车速能够很好地跟踪目标车速，且电池SOC维持在0.4~0.8的目标范围内，说明电池参与了需求功率的分配，证明本文提出的策略有效。由图6可知，相比基于规则控制，本文所提出的策略能保证发动机的输出功率在大部分时间内都较为平稳，仅在功率较低时变化较快。

图4 良好路面高速工况车速跟随的仿真结果

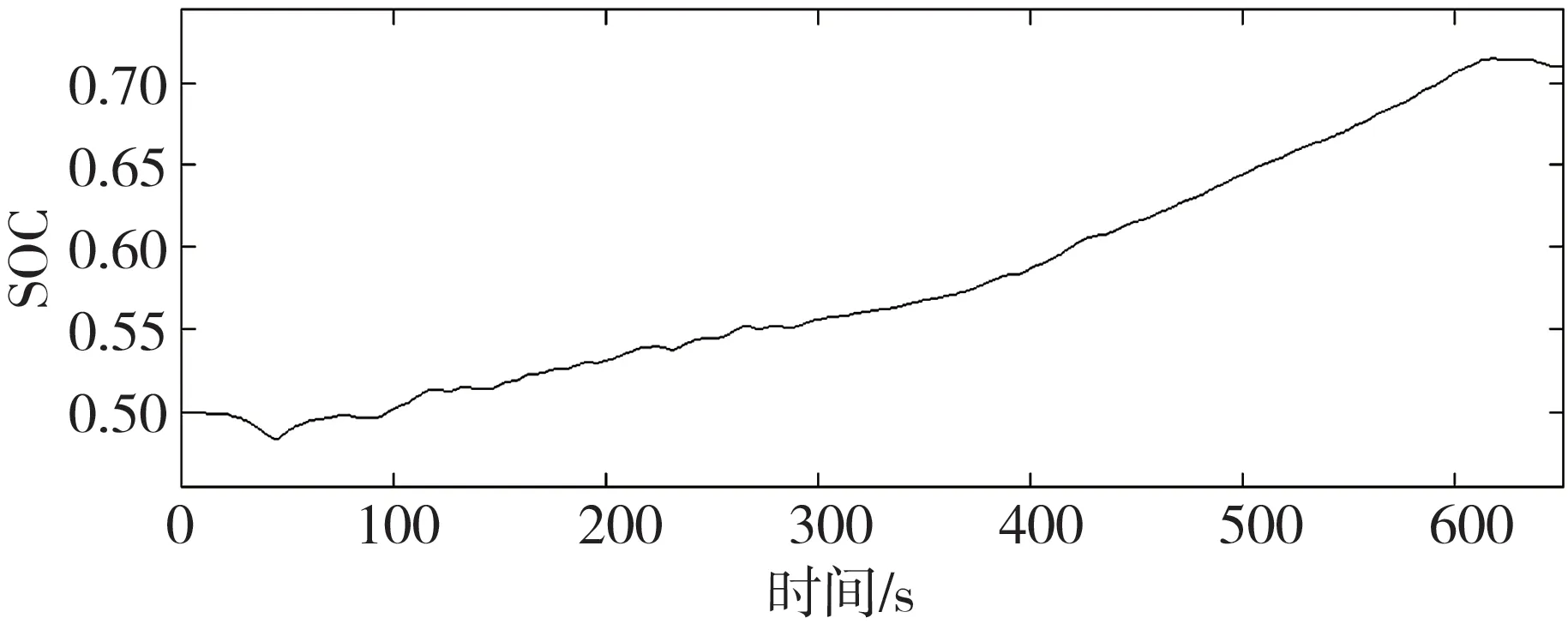
图5 良好路面高速工况电池SOC的仿真结果

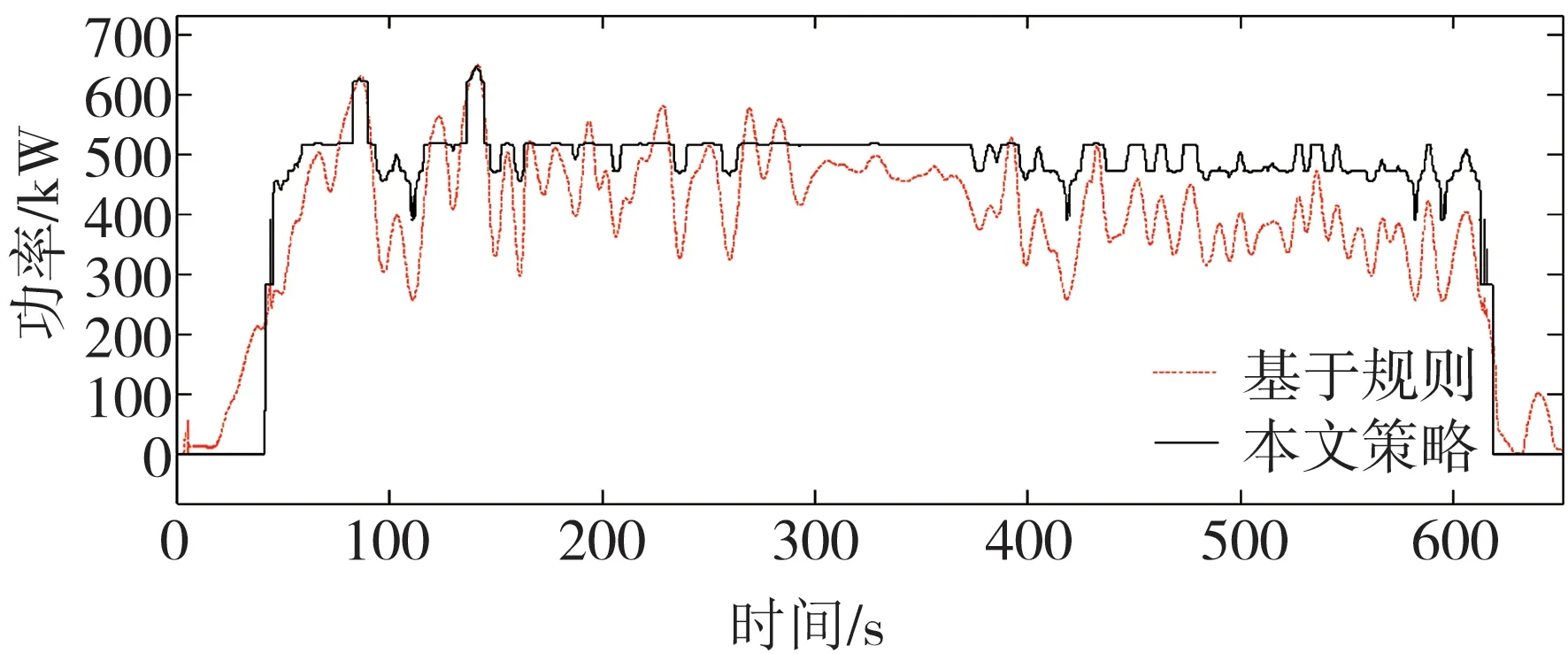
图6 优化前后发动机的需求功率

从图7中可以看出，基于本文所提出的能量管理控制策略，发动机的实际输出功率较为平稳，且发动机发电机组的转速大部分时间内保持不变。此外，母线电压值最低为824 V，相较于额定电压900 V低约76 V，小于规定的最大偏差值150 V，因此满足车辆的行驶要求。此外，发动机主要工作在转速为3 900 r∕min处的高效区，说明本文策略能提高发动机的燃油消耗率，从而降低整车的油耗。

表1 为环境温度为50℃时不同权重系数λSOH所对应的电池寿命的单位里程损失，当电池寿命要求确定之后，可确定电池寿命的权重系数。

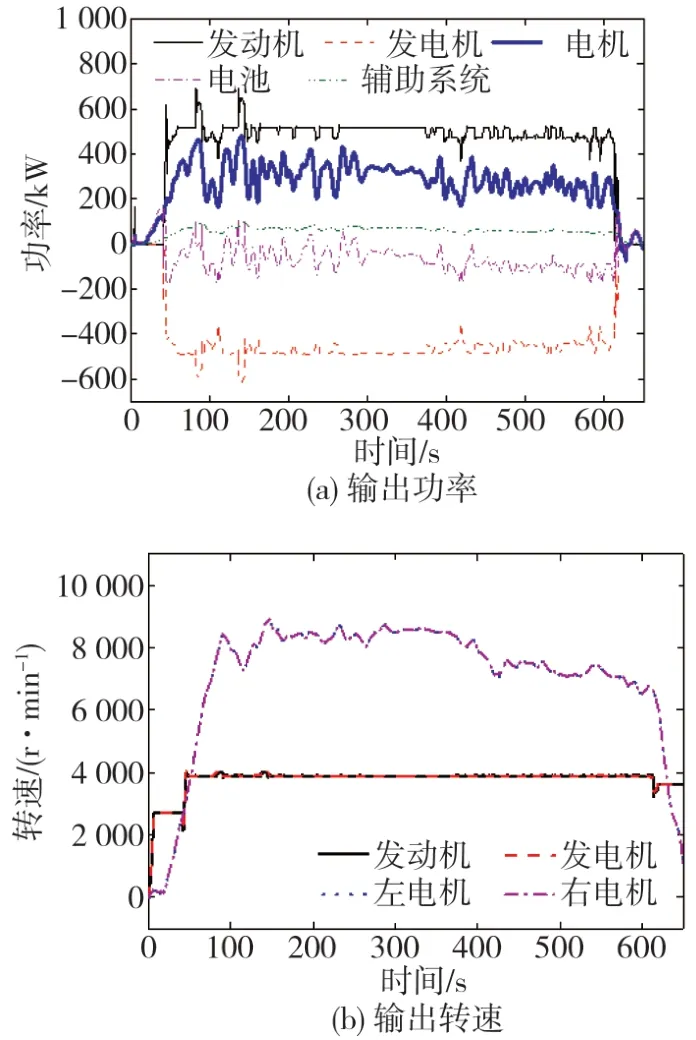
图7 良好路面高速工况仿真结果

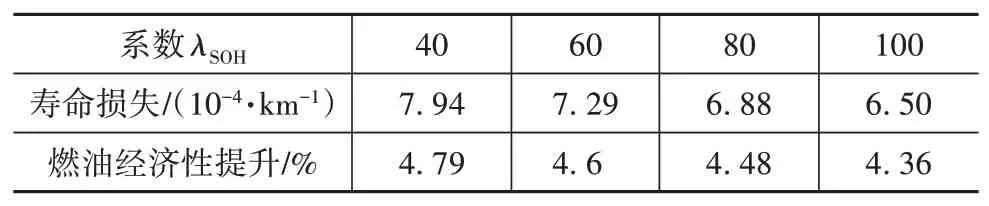
表1 电池寿命损失与燃油经济性仿真结果

3.1.2 越野工况

图8 为越野环境下联式混合动力履带车辆基于规则控制策略和基于本文策略的各部件功率对比结果。针对整体变化趋势而言，基于本文策略的各部件功率变化较为平缓。在t=507 s时，基于规则控制策略的发动机输出功率为283 kW，电池处于放电状态，由于电池被动响应的特性，发动机动态调节过程中目标功率与实际功率的差值均由电池进行补偿，使得电池功率也会发生较大的变化，电池的输出功率高达500 kW，这不仅会影响锂电池的寿命值，同时由于电池与母线直接相连，中间没有DC∕DC稳压装置，电池的大功率放电可能会使得电池输出电压明显下降，超过母线电压的允许工作范围。

而基于本文策略的发动机输出功率为505 kW，电池处于充电状态，因此当需求功率在下一时刻突然增加时，电池的最大放电功率大大降低，进而使得母线电压维持在规定范围内。母线电压的仿真对比结果如图9所示。

3.1.3 电磁炮使用工况

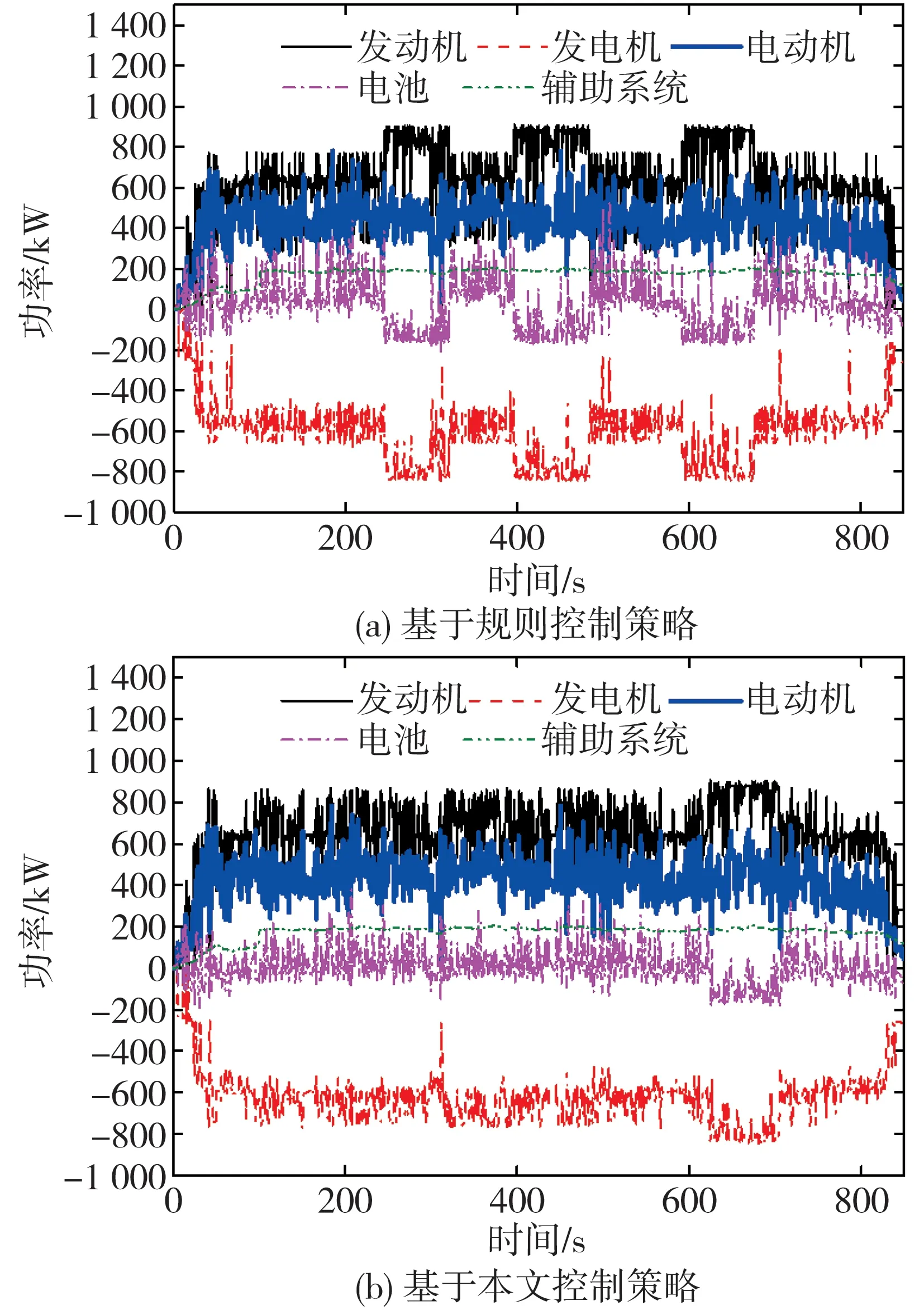
图8 越野工况各部件功率仿真结果

图9 越野工况母线电压的变化

履带车辆处于战时工况时，发射电磁炮一般需要较高的功率需求。电磁炮的需求功率一般可以峰值功率为200 kW的阶跃信号进行模拟，仿真结果如图10所示。由图10可以看出，在t=40 s时，车辆进入电磁炮使用模式，此时所涉及的能量管理策略使得发动机发电机组的输出功率提高，为电池充电，母线电压开始上升；在t=50 s时电磁炮开始发射，用电设备需求功率增加200 kW，而发动机发电机组输出功率维持不变，电池由充电状态改为放电，母线电压下降。在整个过程中，电池的最大输出功率为110 kW，发动机输出功率较为平稳，母线电压始终保持在820 V以上，保证了整车动力性和用电设备的正常使用。

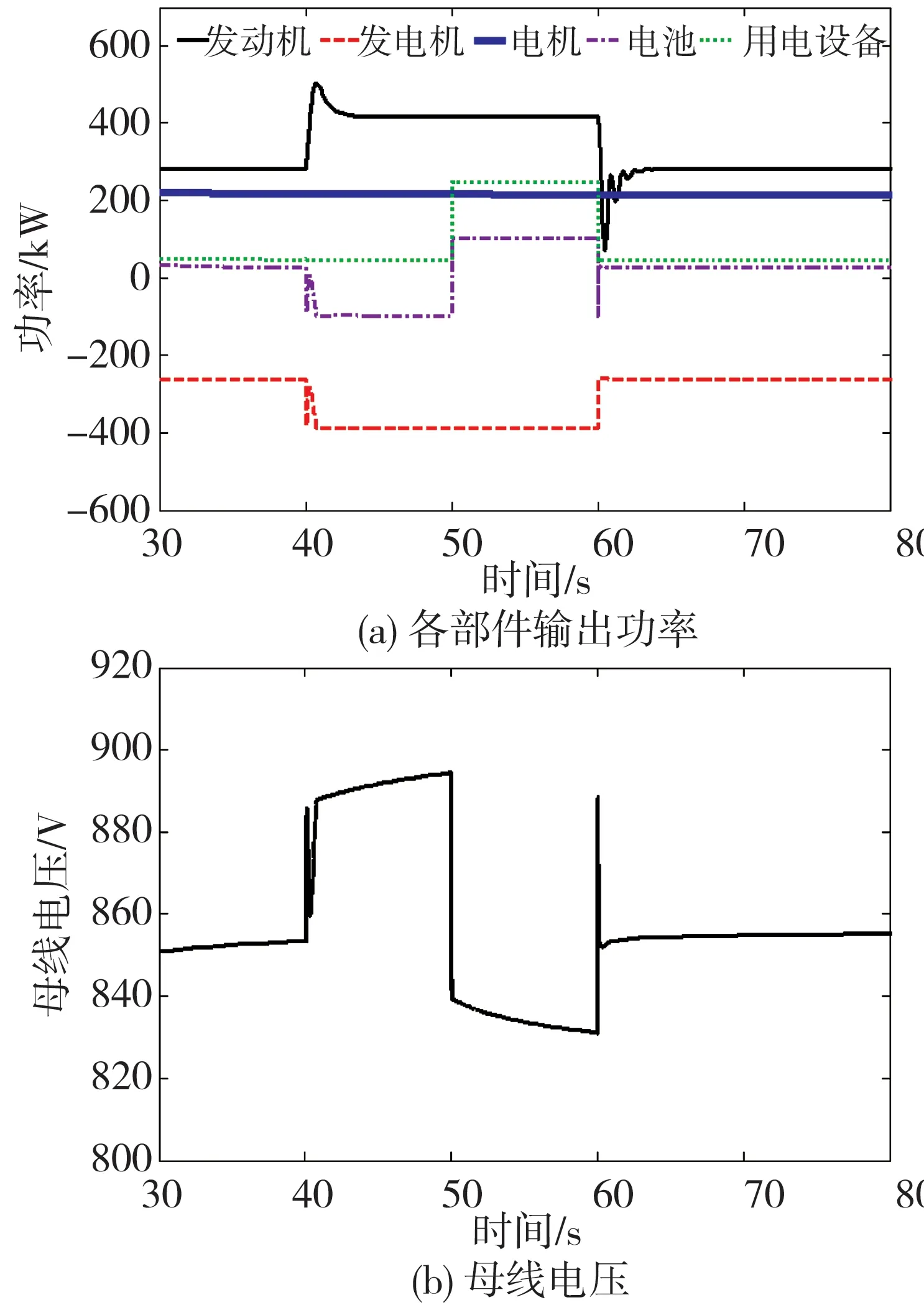
图10 电磁炮使用工况仿真结果

3.2 整车能量管理策略硬件在环测试

所搭建的硬件在环实验实物平台如图11所示，主要包括整车控制器模型、实时仿真平台和上位机3个部分，车辆控制器模型通过Simulink自动生成代码并加载到OpenECU M670之中，整车模型则通过Simulink加载到OpenECU M220之中。硬件在环测试平台搭建完成并对Pisnoop进行设置后，即可在3种典型的循环工况下对整车控制策略进行测试以验证其有效性和实时性。

图11 硬件在环实验实物平台

3.2.1 良好路面高速工况

由图12可知，在良好路面下行驶时，硬件在环测试得到的车速及电机转速结果与仿真结果基本一致，发动机输出功率间的差异在10 kW以内，发动机转速差异在10 r∕min之内，说明该能量管理策略具 有一定的实时性，且能够保证车辆的动力性。

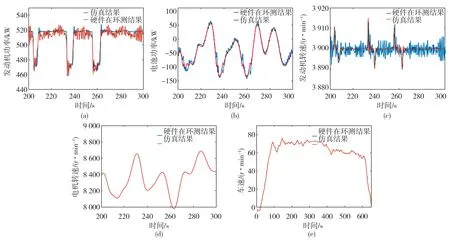
图12 良好路面高速行驶时仿真与硬件在环测试结果对比

3.2.2 越野工况

由图13可知，发动机的转速差异一般在30 r∕min内，功率误差一般在30 kW内，较良好路面的差异大，这是由于越野工况下，整车功率需求变化较快，使得发动机的目标输出功率及目标转速也随之发生较快的变化，由模型精度所带来的差异在一定程度上被放大。

图13 越野工况下硬件在环测试与仿真结果对比

3.2.3 电磁炮使用工况

由图14可以看出，在电磁炮使用工况下，硬件在环与仿真结果趋势相同，但发动机功率在40~60 s内有约7 kW左右的差异，这是由于仿真过程中计算机的求解速度更快，因此采用了更高的求解精度所引起的。

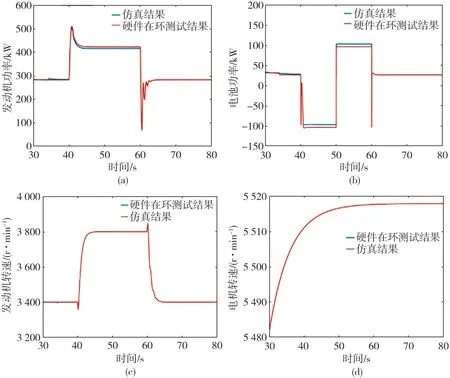
图14 电磁炮工况下硬件在环测试与仿真结果对比

综上所述，本文提出的能量管理策略能够保证履带车辆的动力性能，同时具有较好的实时性，可进一步进行实车验证。

4 结论

本文中以带耦合机构的串联式混合动力履带车辆为研究对象，主要研究了考虑电池寿命时整车能量管理策略的设计。首先，重点细化了电池的模型，考虑温度的影响，建立了电池的2阶RC模型、热模型及其寿命模型。然后，为了更加有效地提高履带车辆的作战半径，提出了一种基于非线性模型预测控制理论的能量管理策略。基于电池的2阶RC模型，建立了用以描述车辆前功率链的未来动态的预测模型，提出了一种计算电池电能等效燃油消耗转化因子的计算方式，并将预测时域内的电能消耗转化为油耗。对于履带车辆不同的行驶工况设计不同的成本函数，运用障碍函数内点法对所提出的非线性优化问题进行求解，并从减少优化变量和缩小变量搜索范围两个方面降低优化问题的计算量。最后，通过仿真及硬件在环测试，在不同工况下对能量管理策略进行验证。仿真结果表明，在良好路面下高速行驶时，相较于基于规则的能量管理策略，本文所提出的能量管理策略在减小系统振荡的同时，燃油经济性明显提高。在越野环境下该策略能够有效降低母线电压的波动，保证了各部件功率的平缓变化。此外，硬件在环测试结果证明了该策略具有良好的实时性，可进一步进行实车测试。