三维边值问题有限差分离散系统预处理的病因抑制策略

张衡，倪振松，郑汉垣

（1.福建技术师范学院a.大数据与人工智能学院；b.无损检测技术福建省高等学校重点实验室，福建福清 350300；2.龙岩学院传播与设计学院，福建龙岩 364012）

偏微分方程的离散系统往往是如下的大型稀疏病态（高条件数）线性方程组[1-2]

其病态问题是制约求解效率和精度的瓶颈[3]，因此，求解之前，需要使用预条件技术[4]139-151来减少系统的病态.

预条件技术[4]139-151的关键是构造适当的预条件子[4]93-98，理想的结果是构造出通用的、最优预条件子[5].

目前，病态问题的解决仍然处在治标不治本的状态.一是缺少对病因的研究，难以针对病因提出科学的预处理方法，不能从根本上消除病态[6-8]；二是预条件子的设计缺乏科学依据，多用实验的方法探索和验证；三是对预处理子的功能多用实验结果说明，难以进行科学的定量分析[9-15].目前关于针对病因的预处理方法鲜见有成果发表.

文献[16][17]针对基于非均匀网格有限差分方法形成的二维泊松方程边值问题离散系统，研究病态原理和预处理方法.针对该方程研究病态结构、病态因子、去病因子；利用病态因子估计方程的条件数，利用去病因子消除病态因子的作用，论证了去病因子是最优预条件子[5].

本文针对病因，提出病因抑制策略，来解决三维泊松方程边值问题差分方法大规模求解中的病态问题.针对不同精度差分格式形成的三种离散系统，基于结构分析的策略[17-20]，确定病因.根据病态结构和病态因子的条件数评估方程的原发病态和继发病态；使用去病因子抑制或者消除病态因子的致病作用，消除原发病态.最后的结论说明，不同的离散系统有类似的病态结构、相同病态因子和去病因子，去病因子依然有最优、通用的特性，预处理的过程几乎不增加求解的成本.

1 病态方程的病因抑制方法

利用文献[16][17]提出病态因子、去病因子、病态结构、病态主体等概念，提出如下关于离散系统病态问题预处理的病因抑制策略如下：

1）分析矩阵A的结构，分离出病态因子Z[16-17]，确定矩阵的病态结构[16-17]如下；

其中Z是α×β病态因子[16-17]，A,Q∈Rα×α,P∈Rβ×β，ZPZTT可逆，Cond(P)关于A的阶数一致有界，Cond(ZPZT)是A的阶数α的增函数，

3）确定去病因子H[16-17]，即设计简单的可逆矩阵H.满足ZZTT=HHTT；

4）使用去病因子H作为预条件子，将方程(1)化成

因为Cond(P)关于A的阶数一致有界，这说明HHTT是最优预条件子[5].

上述病因抑制策略是基于病态结构、针对病因的，病态因子就是病因的表达，去病因子的作用是消除或者抑制病因的发作.因此，预处理的关键是确定病态因子和去病因子，本文将针对三维泊松方程边值问题不同精度三种有限差分格式的离散系统，研究病态因子和去病因子，并讨论去病因子的通用性.

2 三维泊松方程边值问题非均匀网格的有限差分方程

2.1 基于非均匀网格的有限差分离散格式

考虑如下三维泊松方程求解问题[4]

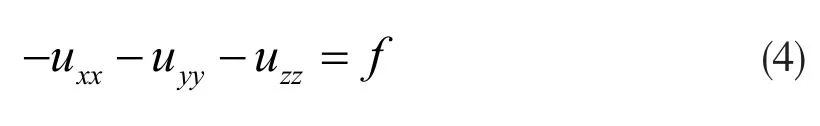
其中u=u(x,y,z) ,f=f(x,y,z) ,(x,y,z)∈∈D= [a1,b1]× [a2,b2]× [a3,b3]⊂R3

根据有限差分方法[5]，对D做非均匀网格剖分[5]：a=x0＜x1＜…＜xn+1=b，

2.1.1 非均匀网格7点差分格式

2.1.2 非均匀网格19点差分格式

则根据4阶精度的泰勒展开式，有

2.1.3 均匀网格27点差分格式

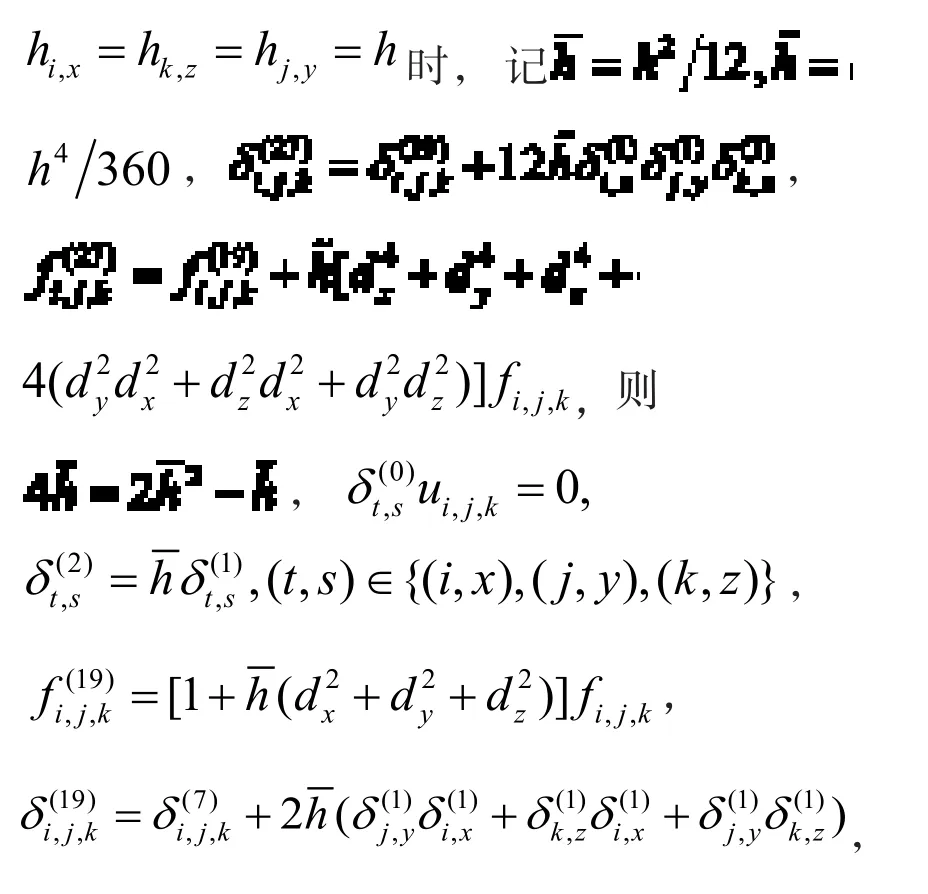
根据6阶精度的泰勒展开式，有

2.2 三维泊松方程边值问题非均匀网格的有限差分方程

记On为n维零向量，In为n阶单位矩阵，

2.2.1 非均匀网格7点差分格式的有限差分方程

向量是已知的，由边界上的网格点以及边界条件确定；因此格式(5)的矩阵形式如下

所以，由格式(5)确定的离散系统为

2.2.2 非均匀网格19点差分格式的有限差分方程

向量是已知的，由边界上的网格点及边界条件确定；格式(6)的矩阵形式如下

因此，由格式(6)确定的离散系统为

2.2.3 均匀网格27点差分格式的有限差分方程

则向量是已知的，由边界上的网格点以及边界条件确定，所以格式(7)的矩阵形式如下

因此，由格式(7)确定的离散系统为

3 有限差分方程的病态因子和去病因子

对于问题(4)的上述三种有限差分方程，通过结构分析，确定它们的病态结构、病态因子以及去病因子.

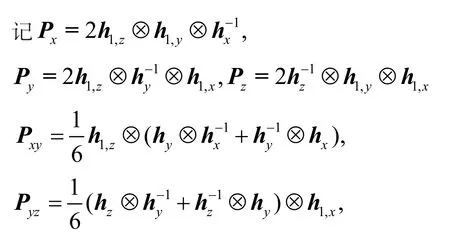
证明：直接验证.证毕.

命题3.

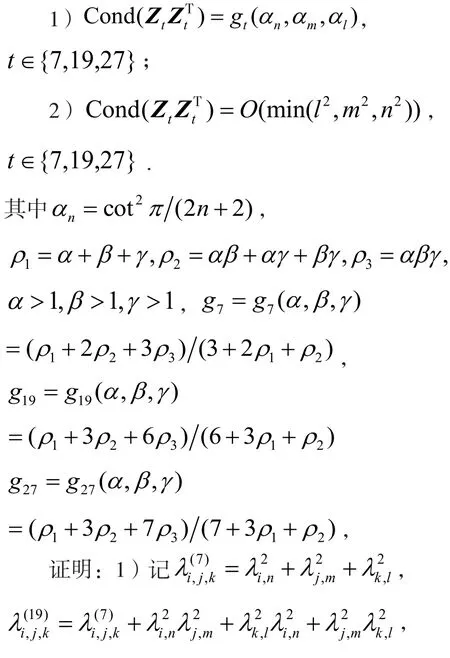
2） 易验证α=O(n2)，记

从而结论成立.证毕

根据命题3结论2），Zt是病态因子[16-17]；根据命题2，矩阵Ht是属于Zt的去病因子[16-17].

命题4.

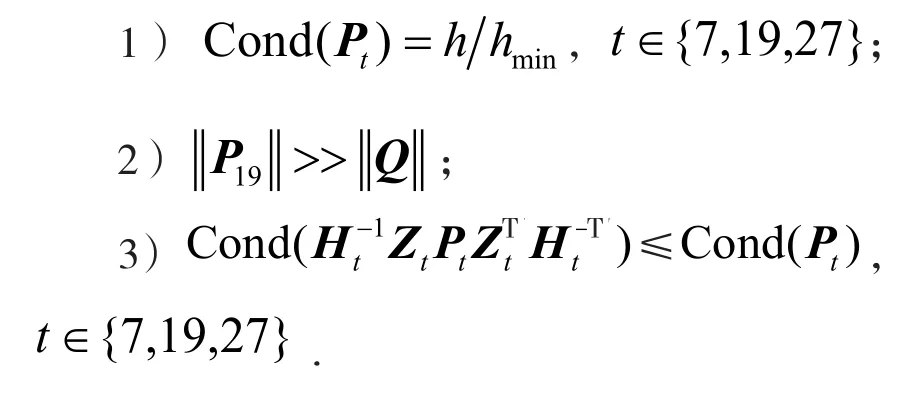
证明：1）可直接验证.

2）根据P19,Q的定义，容易验证因此结论成立.

3）由文献[17]命题1的结论2）可说明结论成立.证毕

根据命题4的结论1），2），式(14)、(15)、(16)表达了At的病态结构[16-17]，Zt是At的病态因子[16-17]；根据命题4的结论3）：Ht是At的最优预条件子[5].

式(14)、(15)、(16)说明差分离散系统 (9)、(11)、(13) 的病态结构都如(2)式，其中At的主要、本质的病态是由病态因子Zt表达的原发病态，来自微分算子，随着离散精度提高，At的规模增加；At的其他病态是由Pt表达的继发病态，受网格大小影响，可以随着应用问题的不同而不同，几乎不受At的规模影响，是非本质的，在应用中可以调整；Q对的At病态影响很小.

4 有限差分方程去病因子的通用性

命题5：

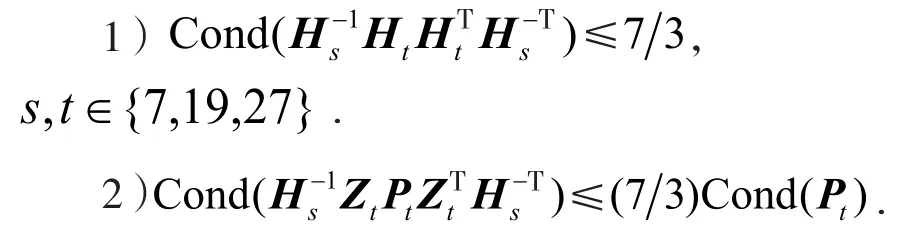
证明：

根据命题5结论2），Hs是的最优预条件子.这说明：基于不同精度、不同步长差分格式的离散系统虽然不相同，仍然有通用的最优预条件子.

使用病因抑制方法对差分方程(9)、(11)、(13)进行预处理，是使用它们的去病因子Hs作为预条件子，将方程(9)、(11)、(13)化为方程(3)的形式，Hs的结构都是确定、简单的，都是由离散正弦变换矩阵的直积Ω与对角矩阵构成预处理中的主要计算是Hs与向量的乘积，每次需要的计算操作数都是有限次离散快速正弦变换的计算量O(mnmnll o g2(nml))，因此预条件子的构造和预处理计算都是低成本的.

预处理后，系统(9)、(11)、(13)的系数矩阵仍然都以正定对称矩阵为主体，所以适合与任何求解方法相结合，完成求解.

5 结论

1）三维泊松方程边值问题的有限差分离散系统中，病态因子表达的原发性病态是微分算子造成，是主要的、本质的，抑制了病态因子的作用，就消除了原发性病态.

2）对于同一个微分算子，使用相同的网格，不同精度差分格式产生的有限差分方程组虽然不同，但是它们有类似的病态因子，对应的去病因子也类似，因此它们消除原发性病态的预处理方法与成本一致，基本不受差分格式的精度影响.

3）继发性病态由P7,P19,P27表达，它们的条件数由网格比的大小和边值条件决定，几乎不受方程阶数的影响，当使用一致网格时，都是常数，Q=0，因此，可以通过调整网格的大小比减少或者消除继发性病态.

4）从病态因子和去病因子的构成可以看出，病态因子和去病因子都是相对独立的，它的元素与边值条件、网格大小都没有关系，不同的差分方程，可以有类似的病态因子，因此去病因子可以通用.