基于MATLAB的离散系统分析

李亚文

（商洛学院 物理与电子信息工程系，陕西商洛 726000）

MATLAB的离散系统的数学理论很早已经形成，直到20世纪90年代计算机应用和发展，才使得其得到了广泛的应用[1]。离散系统的研究存在众多科学领域，比如：信号处理与通讯、图像处理、信号检测、地质勘探、道路检测等[2-3]，前期通过对离散信号特性、离散系统的特性进行数学演算分析，可以判断系统是否是物理可实现的系统，并能进一步优化系统特性[4]。本文摒弃了常规使用数学数值计算或者罗斯准则求解零极点，进而分析系统特性；利用时域分析和频域分析法研究离散系统响应，借助MATLAB软件通过分析系统函数特征,间接研究离散系统的因果稳定性幅频特性和相频特性，为研究离散系统中的数字信号传输和离散信号检测提供前提基础。

1 离散系统

系统分为连续系统和离散系统，信号在系统中传输主要研究的物理量是：激励、系统传输特性和系统响应。其中，当系统各个物理量随时间变化的规律不能用连续函数描述时，而只在离散的瞬间给出数值，这种系统称为离散系统。

如图1为信号通过系统传输、处理的框图。f(·)是系统的输入（激励），y(·)是系统的输出（响应），h(·)是系统特性的一种描述。“·”是信号的自变量，可以是连续变量t，也可以是离散变量n。

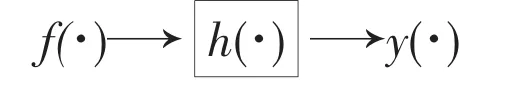
图1 系统分析框图

由于离散系统精度高、自适应性灵活、抗干扰能力强、可靠性好、集成化程度高且成本低[2]，因此其在通信、交通、航天航空、生物医学、遥感等领域得到了广泛的应用。

1.1 LTI离散系统时域响应分析

LTI的离散系统满足可分解、线性以及非时变特性。线性时不变连续系统是由常系数微分方程描述的，而线性时不变离散系统是由常系数差分方程描述的。在差分方程中构成方程的各项包含有未知离散变量的 y(n)，以及 y(n+1)，y(n+2)，…，y(n-1)，y(n-2)，…。

图2 离散系统响应框图

N阶LTI离散系统的数学模型是常系数N阶线性差分方程一般形式[1]

a0y(n)+a1y(n-1)+…+aNy(n-N)=b0x(n)+b1x(n-1)+…+bmx(n-M)或者表示为

分析N阶LTI离散系统时域响应就是求解N阶线性差分方程的过程。时域分析法是将离散系统的响应划分为零输入响应和零状态响应[3]，即y(k)=yzi(k)+yzs(k)，其中零输入响应是齐次差分方程的解，零状态响应可由卷积积分的方法求解,

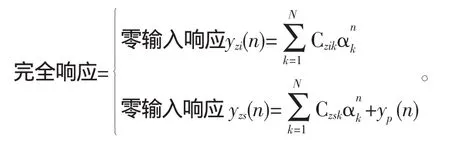
1.2 LTI离散系统频域分析

直接求解离散时间信号通过系统的响应较为复杂，因此，引入频域分析去求解离散系统的时域响应，也称为Z域响应。Z变换的定义[4]可由抽样信号的拉氏变换引出，表示为

在Z域中分析N阶离散系统的时域响应，步骤如下：

2）对N阶的离散差分方程两边同时取Z变换：

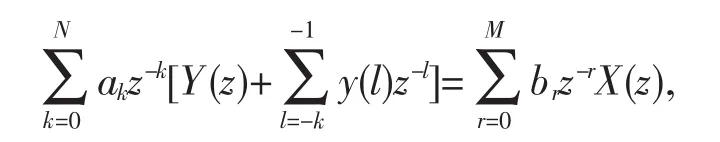
其中y(l)是初始条件。

3）代入系统的初始条件y(l)，进而可得系统响应 Y(z)。

4）对系统响应Y(z)进行逆Z变换，最终可得离散系统的时域响应y(n)。

2 离散系统特性分析

2.1 系统函数

当外加的激励信号x(n)是因果序列时，并且系统初始条件为零（y(l)=0,-N≤l≤-1），因此，系统的响应就是零状态响应，即：Y(z)=Yzs(z)。

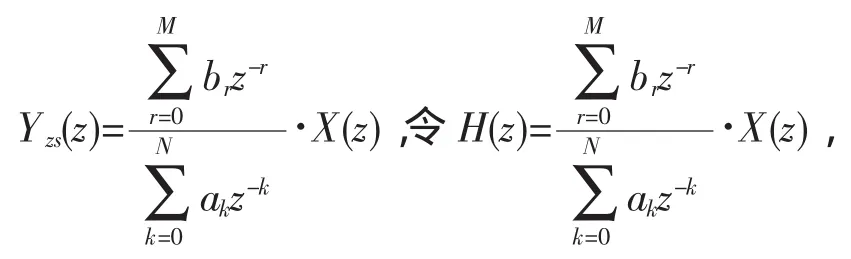
称H(z)为系统（传输）函数，定义LTI离散系统输出Z变换与输入Z变换之比为系统函数[5]

根据系统函数对应的单位冲击响应，将离散系统划分为：有限脉冲响应FIR（finite impulse response）和无线脉冲响应IIR[6-7]（infinite impulse response）。

2.2 离散系统特性

H(z)与h(n)是一对Z变换对，所以只要知道H(z)在z平面上的零、极点分布情况,从而得到系统的脉冲响应h(n)的变化规律。系统函数不但能反应系统的内部结构，并且能较好的反应系统的因果稳定性[7]。

1）因果性

由因果系统的时域条件n＜0，h(n)=0及H(z)的定义，可知因果系统的H(z)只有z的负幂项，其收敛区为RH-＜|z|≤∞。因此收敛区包含无穷时，必为因果系统。

2）稳定性

3 离散系统分析

由系统的电路模型，根据电路关系中电流KCL和电压KVL关系得到输入外加激励和系统响应的数学关系，进而求解系统响应；引入频域分析，研究离散系统的系统传输函数分析零极点分布进而分析离散系统因果稳定性，系统响应的幅频特性和相频特性[8-9]。举例分析一个离散系统。

某离散系统的数学模型

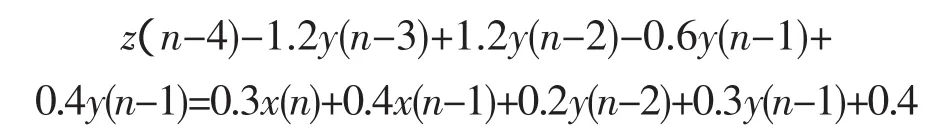
通过分析系统函数，则可研究离散系统特性，由离散系统的数学模型，对差分方程两边同时取Z变换，得到系统传输函数

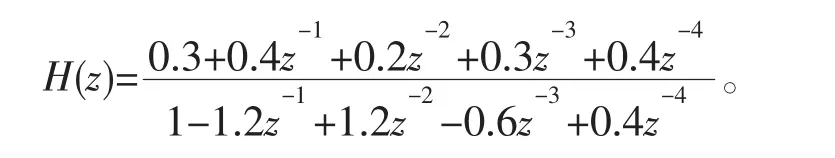
绘制零极点图，matlab部分关键语句

B=[0.30.40.20.30.4];

A=[1-1.21.2-0.60.4];

[r,p,k]=residue(B,A)

zplane(B,A)

p1=abs(p)

a1=angle(p/pi)

零极点图分布如图3所示。

图3 零极点图分布

分析零极点图图3发现，极点都位于单位圆内，因此该离散系统是个因果稳定的系统[10]。

可以看出，通过判断系统极点是否位于单位圆内来判断系统的稳定性，对于一个复杂的系统来说，求极点并不容易，以往总是使用罗斯（Routh）准则[4]判断连续系统的稳定性，利用劳斯（Jury）准则[4]判断离散系统的稳定性。利用matlab软件分析系统稳定性，只需在零极点图上观察即可，判断极点是否位于s的右半平面，或是否有极点在Z平面的单位圆外。

为了分析系统时域响应，因此研究系统的幅频特性和相频特性，如图4所示。

绘制幅频相频特性，matlab关键语句

B=[0.30.40.20.30.4];

A=[1-1.21.2-0.60.4];

[H,w]=freqz(b,a,1000,’whole’);

Subplot(2,1,1); plot(w/pi,abs(H));

Ylabel(‘|H|’);title(‘幅频特性’)

Subplot(2,1,2); plot(w/pi,angle(H));

Ylabel(‘ang|H|’);title(‘相频特性’)

Xlabel（‘omega/pi’）;

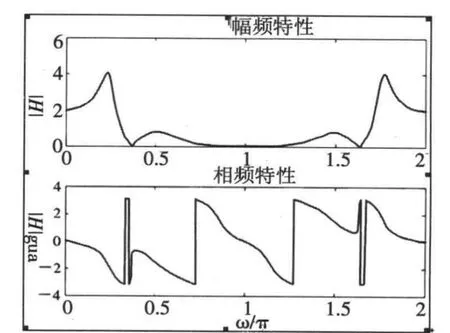
图4 幅频特性和相频特性

通过这个离散系统例子可以看出，借助matlab分析离散系统响应和系统特性比较方便，而且以图形形式显示，较为直观,比传统的数值计算分析系统特性更为精确。

4 结语

离散系统研究成为通信系统和信号处理方面研究的核心内容，既使是连续系统也是将其以适当的步长进行时间离散后，在计算机存储精度下的离散系统，因此实际的通信和信号处理都是离散信号和离散系统的研究。本文主要分析了求解离散系统时域响应的两种方法，即时域分析法和频域分析法，通过分析离散系统系统的特性。借助matlab分析离散系统使过程变得简便，并且图形展示直观形象，这种方法准确率高，简单易于实现，可操作性强，为研究数字通信系统的研究和离散信号分析提供前提条件。

[1]张德丰.matlab在数字信号处理中的应用[M].北京:清华大学出版社,2010:13-15.

[2]郑君里,应启珩,杨为理.信号与系统[M].北京:高等教育出版社,2000:35-46.

[3]陈怀琛.MATLAB及其在理工课程中的应用指南[M].西安:西安电子科技大学出版社,2000:9-22.

[4]AV奥本海姆,AS威斯基.信号与系统[M].刘树棠,译.西安:西安交通大学出版社,1998:75-84.

[5]师五喜,霍 伟,吴宏鑫.一类未知非线性离散系统的直接自适应模糊预测控制[J].自动化学报,2004,30(5):664-670.

[6]于 驰,王宏伟,宫明龙.多输入多输出离散系统的输出反馈滑模控制[J].东北大学学报:自然科学版,2012,33(2):89-97.

[7]WANG Y Z,ZHANG H G,YANG J.Robust adaptive control for interval time-delay systems[J].Journal of Control Theroy and Application,2006,4:367-371.

[8]肖卫初,陈伟宏.MATLAB在IIR滤波器设计与仿真中的应用[J].湖南工程学院学报:自然科学版,2005,15(1):64-71.

[9]李吉祥,武俊峰,樊丽颖.离散系统降阶控制器的设计[J].电机与控制学报,2011,15(6):78-83.

[10]党宏社.信号系统实验[M].MATLAB版.西安:西安电子科技大学出版社,2007:98-115.