低温贮箱用环形金属隔膜翻转过程数值模拟及特性研究
2021-06-07赵继鹏马天驹王颢琨
徐 涛,赵继鹏,马天驹,王颢琨
(兰州空间技术物理研究所,兰州 730000)
0 引言
低温推进剂具有高比冲、高推进效率的特点,在长距离、大推力的应用环境中具有明显的优势。而低温推进系统必不可少的关键部件——贮箱也成为目前研究的热点。由于低温推进剂内部存在复杂的流-固、气-液两相瞬态传热传质现象,表面张力贮箱很难适应这种低温介质复杂相变的情况,严重时会造成管理装置的功能失效。另外,由于低温推进剂多为液氢和液氧,而表面张力贮箱多为钛合金材料,钛合金在液氧中会发生氧化,使其强度下降,而在液氢中又会发生氢脆,造成应力腐蚀,使贮箱的强度大幅降低。因此国内外均不采用表面张力贮箱进行低温推进剂的存贮和管理[1-3]。
金属膜贮箱是一种适用于空间工作的推进剂存贮和管理装置,其膜片与贮箱壳体密封连接,工作中必须保证膜片轴对称变形,刚性膜片可消除推进剂的晃动。工作时增压气体挤压膜片,将推进剂挤入输送管路,实现推进剂的供应。由于金属膜贮箱密封性好、寿命长、质心稳定,根据工作介质对金属隔膜材料进行适当选择可以达到与低温推进剂长期相容的目的,大幅增加了其适应性,被广泛应用在低温推进系统中[4-5]。目前应用于工程中的金属隔膜贮箱多为球形或者球锥形结构,贮箱内部的金属膜片多为球锥形隔膜[6-8],此结构对于安装空间无特殊要求的航天器一般应用较多,而对于空间较为紧张,且需要有导线或者电缆从贮箱内部穿过的结构不能满足需求。环形金属隔膜贮箱作为一种可满足此类特殊需求的金属隔膜贮箱,能够充分利用外围空间,提升航天器的空间利用率。
环形金属隔膜贮箱内部的环形金属隔膜作为贮箱的关键部件,其结构形式直接影响着贮箱的性能。以往学者均对常规的球形金属隔膜进行了研究,对环形金属隔膜特别是其翻转性能的研究还未见报道。环形金属隔膜的翻转特性由其启翻压力、启翻位置及翻转过程中的偏心来表征,这些因素直接受隔膜结构尺寸的影响,尤其受厚度影响较大。实际使用过程中,由于安装空间的限制,隔膜构型一旦确定就不会改变,而多是通过改变隔膜的厚度分布来实现对隔膜翻转性能的调整。本文将建立不同厚度环形金属隔膜的非线性有限元模型,期望通过对隔膜翻转过程的模拟仿真,得出厚度参数对翻转特性的影响,并通过实验进行验证。
1 膜片结构
环形金属隔膜由圆环段、内翻边、内锥段、外翻边和外锥段组成,图1是环形金属隔膜的结构示意图。内翻边和外翻边为圆弧状,内翻边和外翻边的位置决定隔膜的启翻位置,其半径和厚度决定隔膜的翻转压力Δp。Δp[9]可用式(1)表示:
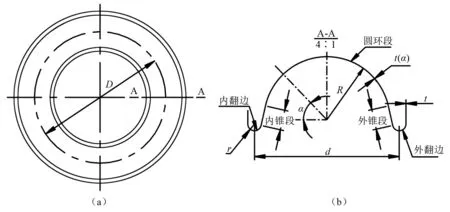
图1 环形金属隔膜结构示意图Fig.1 Schematic diagram of annular metal diaphragm
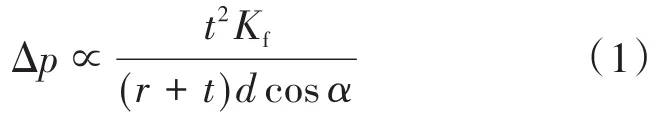
式中:Δp为翻转压差,MPa;t为翻边位置厚度,mm;r为翻边位置半径,mm;Kf为变形强度,MPa;d为翻边初始直径,mm;α为翻边位置与水平方向夹角,°。
从式(1)可以看出,当金属隔膜的几何结构确定后,隔膜的翻转压差随翻转过程中翻边的位置不同而不断变化。当α达到90°时,翻转压差为无穷大,但实际翻转过程中,翻转压差总是有限的。随着隔膜翻转过程的进行,隔膜翻边位置的厚度及半径均会发生变化。随着隔膜翻转材料被拉伸,隔膜厚度会变小,翻边位置的半径会变大,最终使得金属隔膜的翻转压差在有限的范围内变化。
在实际金属隔膜设计过程中,最重要的是保证金属隔膜翻转过程的稳定进行,即翻转过程中金属隔膜只发生翻转而不发生屈曲,始终满足Δp<p屈(p屈为一阶屈曲极限),否则,金属隔膜就会失效。由于空间限制,翻边初始直径一旦确定一般不会再改变,因此在金属隔膜的设计过程中多通过改变隔膜厚度来达到上述目的。但是金属隔膜的翻转过程是非线性动态过程,以上设计要求均无法通过解析法实现,只能采用有限元法完成。
2 Riks法简介
几何非线性静态问题有时涉及到屈曲或倒塌性能,即荷载-位移响应出现负刚度(下降段)且结构必须释放应变能来维持平衡[10]。Riks法可在响应的不稳定阶段获得静态平衡解,该方法可用于荷载幅值由单个标量参数控制的情况,在预制初始缺陷类问题方面,可以获得准确的解。Riks法的本质是在求解平衡方程式(2)的同时,满足增量位移的球面约束方程式(3)。
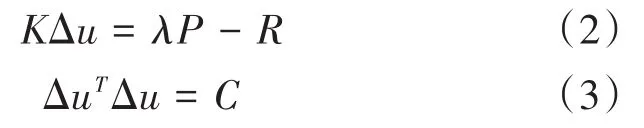
式中:K为当前增量步的刚度矩阵;Δu为当前载荷产生的位移,mm;λ为载荷方法系数;P为当前载荷,Pa;R为上一增量步产生的残差;C为弧长的平方,mm2。
从以上方程可知,当前增量步载荷的大小必须在一个以增量步开始时刻的位移为向量的中心,弧长为球面的空间中产生一个位移增量。通过在每个增量步求解式(2)和式(3),即可得到不同载荷下模型的失稳形态。Riks方法采用将荷载幅值作为附加的未知数,同时求解荷载和位移。Riks方法特别适用于求解预制初始缺陷类问题,如极限荷载问题或大多数不稳定问题。
3 有限元模型的建立
采用四边形壳体单元(S4R)建立环形金属隔膜的有限元模型。由于纯铝在常温和低温情况下力学性能变化不大,实际应用时均选用纯铝作为金属隔膜材料,纯铝材料机械性能如表1[11-13]所列。

表1 纯铝的机械性能Tab.1 Mechanical properties of pure aluminum
将环形金属隔膜内环直边和外环直边固定,对隔膜外表面施加翻转压差Δp,计算过程中采用Riks法进行求解。为验证隔膜厚度对隔膜翻转特性的影响,首先建立等厚度金属隔膜的有限元模型,考察不同厚度及翻边半径对金属隔膜启翻压力、翻转压差及质心偏移的影响。之后,对金属隔膜的厚度进行优化,建立变厚度金属隔膜的有限元模型,并与等厚度金属隔膜的翻转进行比较。
4 计算结果与分析
4.1 等厚度金属隔膜结果分析
对所建立的0.6 mm厚的金属隔膜的有限元模型,用ABAQUS大型非线性结构分析软件进行计算和分析,共运算了421个增量步。图2是不同增量步时等厚度金属隔膜的翻转过程应力云图,可以看出,隔膜在翻转过程中,翻边位置均发生了塑性变形,最大应力达到了75 MPa。整个过程中,翻边位置的应力一直处于较大的状态,但隔膜均能够顺利翻转,证明等厚度的隔膜也能够实现翻转。
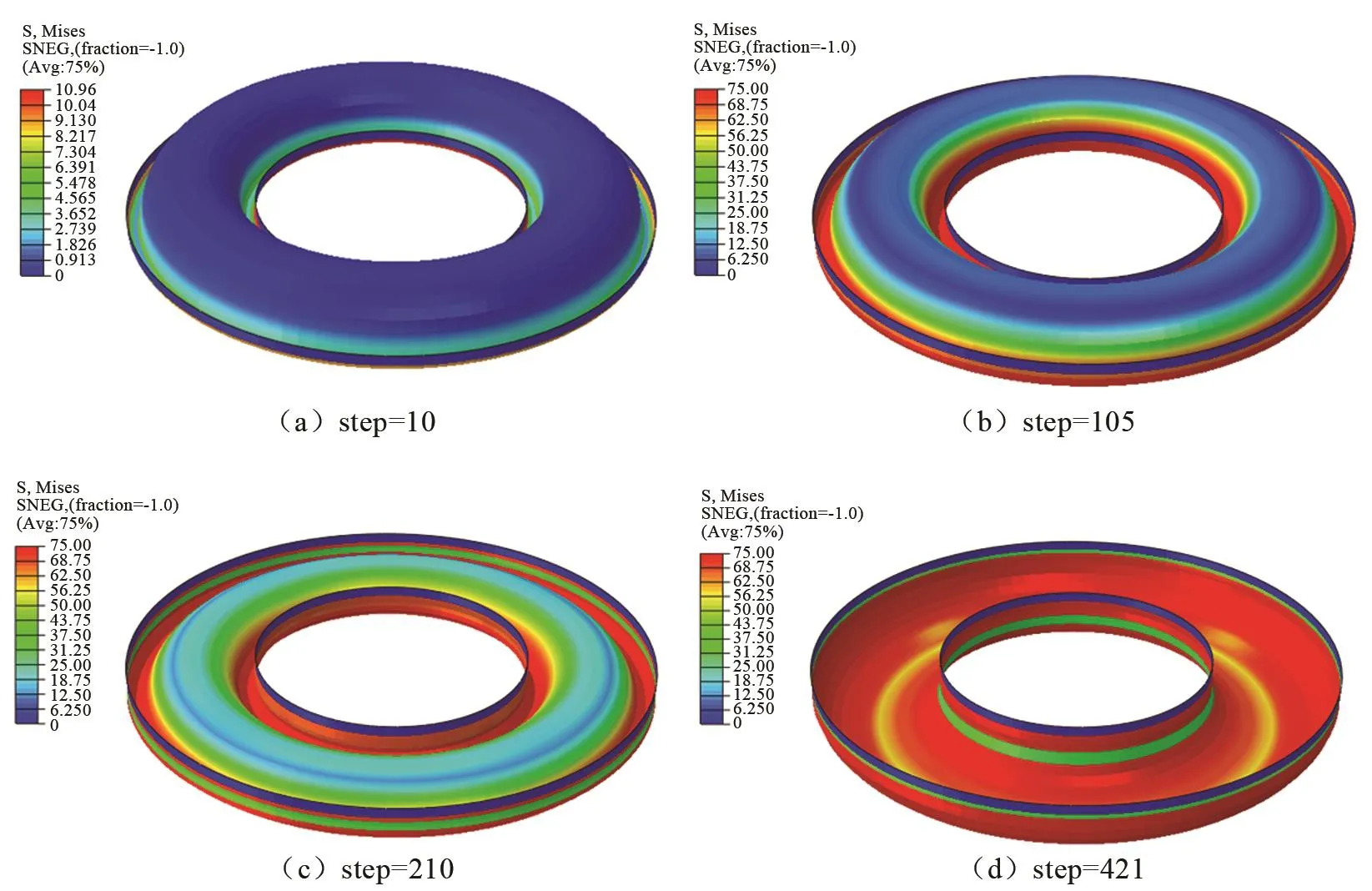
图2 不同的增量步时等厚度金属隔膜翻转应力云图Fig.2 The colored stress patterns of unique thickness annular metal diaphragm in flipping
图3是隔膜翻转到不同位置时其最大塑性应变随隔膜顶点位移变化的曲线。可以看出,隔膜在翻转过程中均发生了塑性变形,最大塑性应变达到0.18,但此塑性应变小于材料的最大塑性应变0.3,材料在翻转过程中不会被破坏。
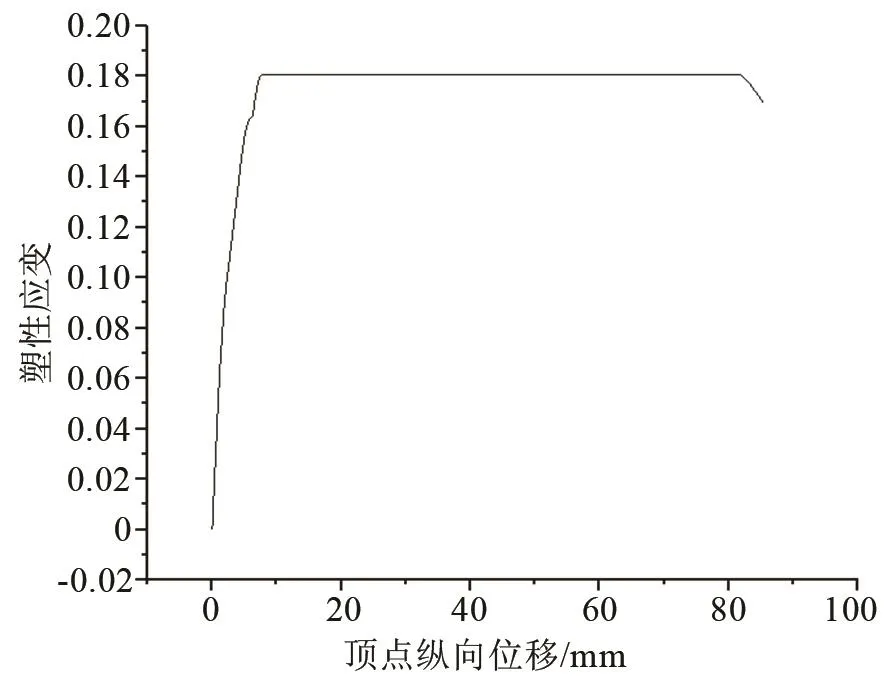
图3 隔膜翻转到不同位置时最大塑性应变随隔膜顶点纵向位移变化曲线Fig.3 The maximum plastic strain changes with the displacement of the diaphragm top when the diaphragm is turned to different positions
由于无法直接通过有限元分析计算获得质心位移随翻转进行的变化情况,在实际设计过程中只能通过考察隔膜翻转到不同位置时其顶点的侧向位移来表征翻转过程中隔膜质心的变化情况。图4(a)是不同厚度的等厚度隔膜翻转过程中顶点侧向位移与顶点纵向位移的关系图。从图中可以看出三种厚度金属隔膜侧向位移的趋势均相同,金属隔膜在翻转初期会发生微小的位移。这主要是由于金属隔膜开始启翻时,其翻转部位为圆锥面形成的锥段位置,此部位刚度较弱,翻转过程中存在一定的不稳定性。隔膜翻转快结束时,隔膜中心位置位移最大。另外还发现,随着金属隔膜厚度的增加,其后期侧向位移增大。图4(b)是不同厚度的等厚度隔膜翻转压差与顶点纵向位移的关系图。从图中可以看出,随着隔膜厚度的增加,其翻转压差也会随之增加。隔膜厚度越小,相应的翻转压差越小,这有利于降低整个系统的压力。因此在实际的设计过程中,力求将隔膜的翻转压差降到最小,以减小系统的压力,减小系统质量。为此,在后续设计过程中,采用0.4 mm等厚度金属隔膜进行了有限元分析,得到的应力云图如图5所示。
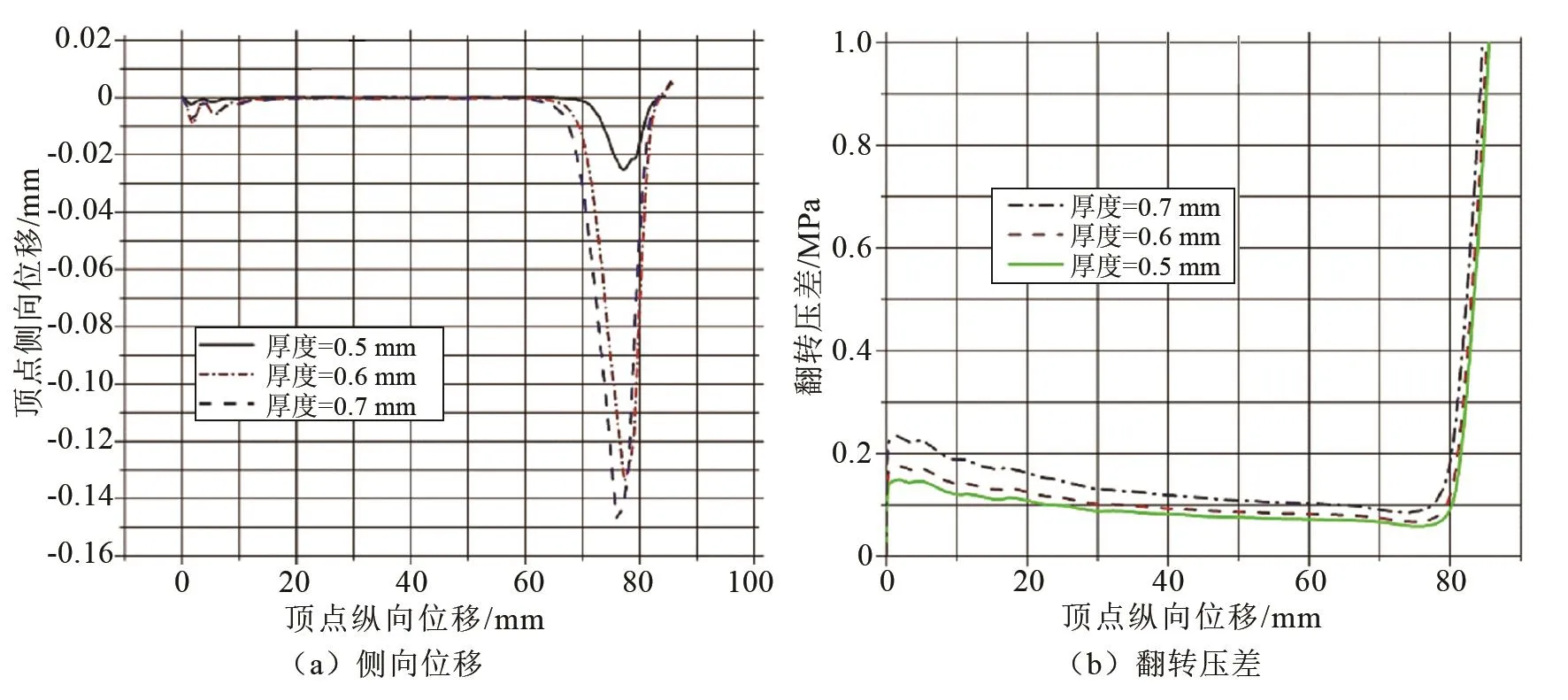
图4 侧向位移及翻转压差与顶点纵向位移关系图(等厚度)Fig.4The curve of maximum plastic strain with the displacement of the diaphragm top point(unique thickness)
图5中金属隔膜在前期依旧可以顺利翻转,随着翻转的进行,翻边位置越来越接近圆环截面中间位置。此时,截面中间位置趋近于平面结构,其刚度明显下降,而隔膜的翻转压差却继续增加,使此形态下的隔膜翻转压力超过了其屈曲强度,造成隔膜失效。为了解决翻转后期的金属隔膜失效的问题,考虑采用变厚度的结构进行金属隔膜的设计,以此降低金属隔膜的翻转刚度,保证在翻转过程中,金属隔膜的翻转压差始终小于其一阶屈曲极限强度。

图5 0.4 mm等厚度金属隔膜翻转变形应力云图Fig.5 The colored stress patterns of unique thickness annular metal diaphragm in flipping(thickness=0.4 mm)
4.2 变厚度金属隔膜结果分析
图6是变厚度隔膜的翻转变形云图,图7是变厚度隔膜的厚度分布云图。从变形云图中可以看出,变厚度隔膜不会再发生等厚度隔膜翻转后期的屈曲失稳,可以顺利翻转。图8是变厚度隔膜翻转压差曲线,从图中可以看出,经过优化后的变厚度隔膜翻转压差较等厚度隔膜均有所减小。采用变厚度隔膜能够解决壁厚较薄的隔膜翻转过程中屈曲失稳的问题,并且其翻转过程中的翻转压差较等厚度隔膜低。对隔膜的厚度进行优化,能够得到翻转性能更加优异的结构形式。

图6 变厚度金属隔膜翻转变形云图Fig.6 Overturning deformation nephogram of membrane with variable thickness

图7 变厚度隔膜的厚度分布云图Fig.7 Thickness distribution of variable thickness diaphragm
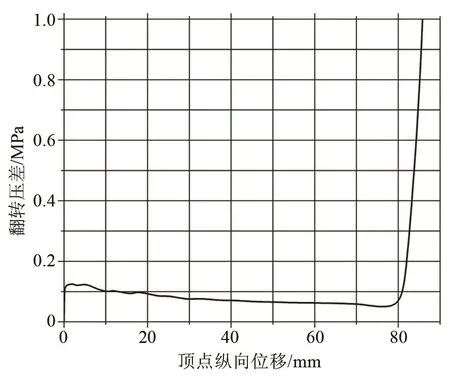
图8 变厚度隔膜翻转压差随纵向位移的变化曲线Fig.8 Turnover pressure difference of variable thickness diaphragm
5 试验验证
为验证所设计的金属隔膜能否正常翻转,采用纯铝加工了如图7所示的金属隔膜,并搭建了试验系统进行翻转试验,试验系统如图9所示,试验结果如表2所列。贮箱采用落压排放的方式进行试验,贮箱内部隔膜顶部粘贴高精度位移传感器用于测量隔膜顶部的侧向位移。压差由连接在贮箱气液口之间的高精度压差计测得。试验前,对系统进行了检漏,以保证系统漏率满足要求;之后,将贮箱液腔充满液体,关闭所有阀门;打开气源,气体通过减压阀减压至0.2 MPa后,打开贮箱液口,进行排放试验。
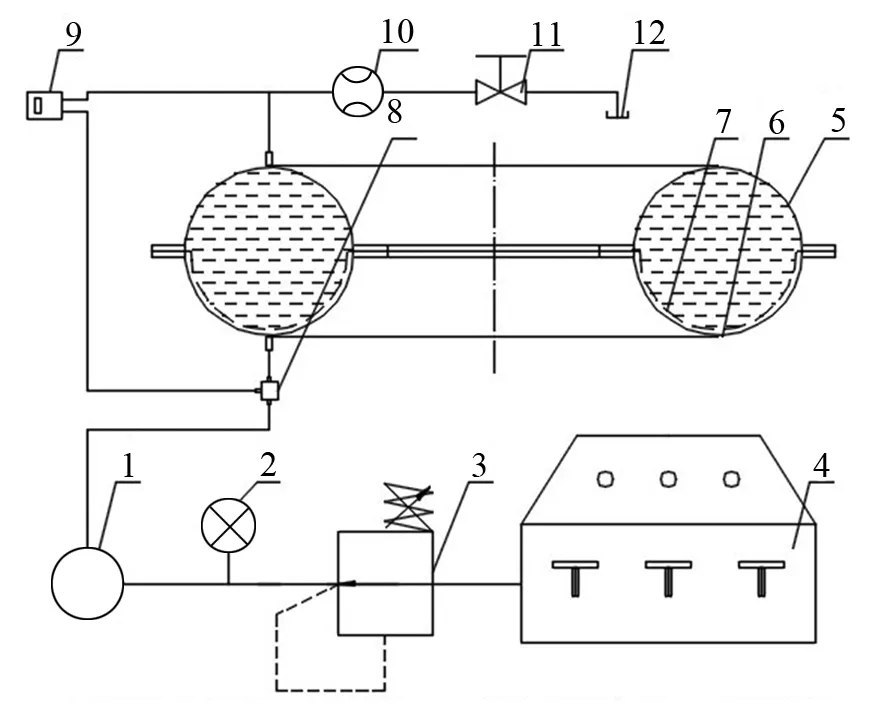
图9 翻转试验系统示意图Fig.9 Flip test system
从试验数据可以看出,压差的测量结果与有限元分析结果趋势一致,但实测结果与设计结果存在一定的偏差。这主要是由于实际加工的隔膜的构型及厚度尺寸与设计结果均存在误差,导致隔膜实物翻转过程与理论设计的翻转过程存在一定的差别。另外,从表2中可以看出隔膜纵向位移在0~40 mm之间时,理论计算值与实测值偏差在10%以内。随着翻转的进行,纵向位移在40~80 mm之间时,偏差较大。翻转前期,隔膜与液腔壳体贴合面积较小,隔膜处于理想的翻转状态,随着隔膜与液腔贴合面积的增加,液腔壳体对隔膜翻转的影响突显,而在设计过程中并未考虑此因素对隔膜翻转特性的影响,加上实际加工的隔膜与理论设计的差异,最终使实测结果与有限元计算结果产生偏差。
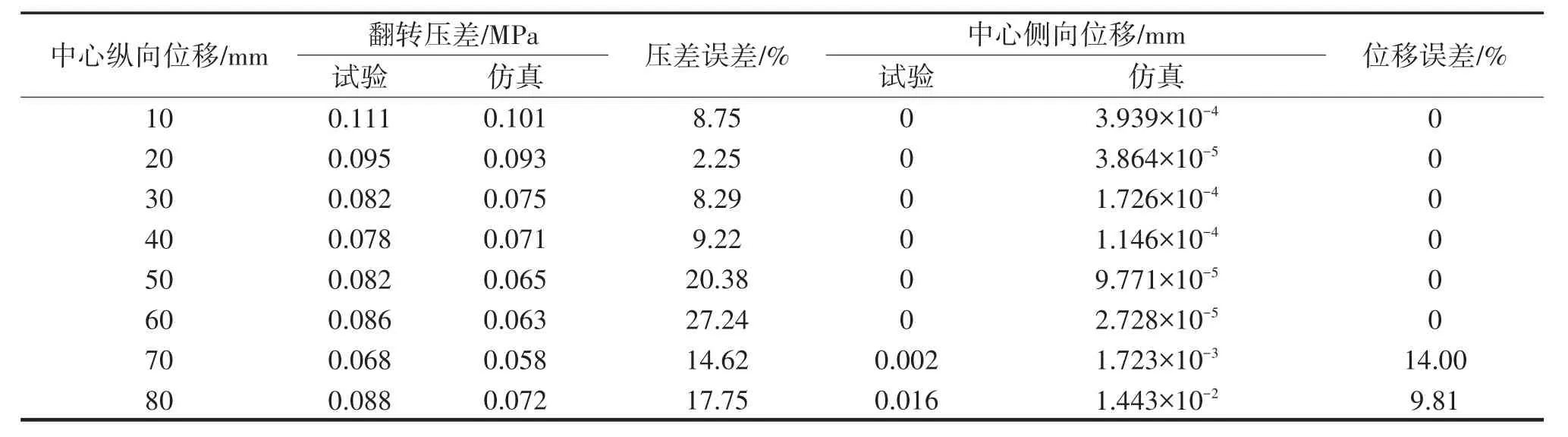
表2 金属隔膜试验结果Tab.2 Diaphragm test results
由于环形金属隔膜刚性较好,纵向位移在0~70 mm之间时,顶点的侧向位移非常小,采用高精度位移传感器无法测得。快完成翻转时(纵向位移在70~80 mm之间),由于隔膜翻转变形的积累及壳体对隔膜的作用,隔膜侧向位移增大。
6 结论
(1)研究发现,变厚度环形金属隔膜是一种理想的隔膜形式。
(2)等厚度的铝合金环形金属隔膜可以顺利实现翻转。隔膜在翻转过程中,翻边位置的最大应力达到了75 MPa,隔膜翻边位置均发生了塑性变形。整个翻转过程中,翻边位置应力一直处于较大的状态,但塑性应变小于材料的最大塑性应变,材料在翻转过程中不会被破坏。
(3)变厚度隔膜能够解决壁厚较薄的隔膜翻转过程中屈曲失稳的问题,并且其翻转过程中的翻转压差较等厚度低。对隔膜的厚度分布进行优化,能够得到翻转性能更加优异的隔膜结构。
(4)变厚度金属隔膜的翻转试验结果表明设计,结果和测量结果趋势一致,但存在一定的误差,该误差是由加工误差引起的。贮箱液腔限位对隔膜翻转过程的影响也会使隔膜的实测结果与设计结果产生一定的误差。
