Ce3Th合金高压相变的第一性原理研究*

2021-06-07陈南迪曾召益胡翠娥

功能材料 2021年5期

陈南迪，王艳，曾召益，胡翠娥

(重庆师范大学物理与电子工程学院, 重庆 401331)

0 引言

金属铈(Z=58)和钍(Z=90)分别位于镧系和锕系过渡金属系列的起始位置，外层电子分别为4f和5f。铈是地壳中丰度最高的稀土元素，因其不具有放射性和毒性，多年来，一直是许多研究者的研究对象。铈是一种典型的窄带金属，由于f电子对压力和温度等外部影响的敏感性，可能具有多相图[1-4]。金属Ce的结构相变，是在室温下从低密度fcc相塌缩到密度更大的等结构α相，该相变发生在0.8 GPa的压力下，并伴随着17%的体积塌缩.异常体积塌缩通常是由Mott跃迁模型或Kondo体积塌缩(KVC)模型中单个4f电子的不稳定性来解释[5-6]。在我们以前的工作中，预测了纯Ce在压力下的相变路径。从α-Ce(fcc)到α-Ce(单斜晶系)，再到bct-Ce的转变分别发生在5.36 GPa和14.37 GPa[4]。然而，Th的相图比Ce简单得多，它没有中间相，且相变压稳定低于从fcc到bct的相变压。

稀土元素 Ce有着特殊的电子层结构，其4f电子层未填满，且第五层电子壳层很好的屏蔽了第四层电子，4f电子层几乎不受其他邻近离子的势场影响，这使得Ce具有独特的电磁特性，Ce基金属间化合物也因此得到了广泛的研究，目前已经被应用于航天，军事和医疗等方面[7-9]。铈是众多稀土元素中综合性能较高的合金元素，压力和温度对Ce基合金和化合物的结构也有着很大的影响[10-15]。Harris等[16]的实验结果表明富Ce合金中Ce的有效原子直径随温度的变化而不断变化。在室温下，合金处于中间状态，其中有效原子直径和相应的有效价值似乎取决于应变能的结果效应和温度因素。在相干电位近似的框架下，Landa等[17]计算了Ce43Th57无序合金为1Mbar。在Ce-Th体系中，从fcc结构到bct结构的相变压力随Th含量的增加而增加。Söderlind和Eriksson[18]对Ce-Th3、CeTh合金和CeTh3化合物在高压低温下的相图进行了较好的研究。当压力超过200 GPa时，CexTh1-x合金显示了一个统一的图像，它们的晶格常数趋于稳定，c/a轴向比接近于1.65。Evans等[12]报道了富Ce的Ce-Th合金在压力下发生体积塌缩。Lawrence等[19]通过对密度和电阻率的测量，研究了以4f电子离域和伴随的体积变化为特征的Ce1-xThx体系的同构相变。到目前为止，对Ce3Th合金的结构相变、弹性性质和热力学性质的系统性理论研究还很缺乏，这是本文研究的主要目的。

1 计算方法

采用基于密度泛函理论的虚晶近似(VCA)在高压下对Ce 4f15s25p65d16s2和Th 6s26p66d27s2进行计算模拟。VCA是通过将元素的赝势进行混合来产生一种新的势函数。我们前期也采用这种方法成功预测了Ce-Th合金随组分变化的相图[20]。在计算中，由于Ce存在f电子，因此需要谨慎处理。我们前期采用密度泛函理论(DFT)+U的方法对纯Ce做了较为深入的探讨[21]。发现f电子在较低的压强区间，对Ce的同构相变起决定性的作用。但是在较高压强区间(同构相变之后)，对fcc-bct的相变影响并不明显，因此，本文采用DFT直接计算较高压强下的fcc和 bct结构的物理性质。在电子结构计算时，使用了CASTEP程序包的平面波赝势方法,交换关联相互函数采用的是广义梯度近似(GGA)框架下的Perdew-Burke-Ernzerhof (PBE)形式[22]，为获得准确的计算结果，我们将Ce3Th合金的电子波函数在截断能为550 eV的平面波基中展开。fcc结构和bct结构的布里渊区分别采用11×11×11 和 11×11×13 Monkhorst pack网格，为保证计算的精度，使总能的收敛精度达到10-6eV/atom。

2 结果和讨论

2.1 结构相变

对Ce3Th合金的fcc-bct相变进行了计算和分析，将得到的fcc相和bct相的体积-压强变化规律与Ce0.76Th0.24[11]和纯Ce[23],纯Th[24]的实验结果进行比较，如图1。我们的结果与已有的Ce基合金和纯Ce、纯Th的体积-压强的变化规律相吻合。在温度300 K时，我们计算了Ce3Th合金fcc相和bct相的能量-体积关系，得到了其各自的状态方程(EOS)，此时0 GPa下的平衡体积V0=0.028 nm3和体积模量B0=50.29 GPa，如表1所示。同时，我们也在表中给出了已有的纯Ce和纯Th的计算值以及实验值进行对照。加入Th后，体积模量和平衡体积分别比纯Ce的实验结果增加43.7%和 0.7% 。

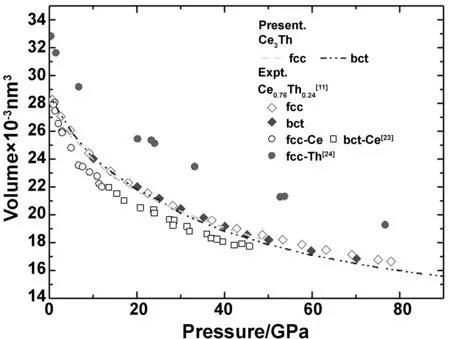
图1 Ce3Th(fcc相和bct相)体积随压强变化的规律，并与已有的纯Ce[23],纯Th[24]的实验结果进行比较Fig 1 Rule of volume change of Ce3Th(fcc phase and bct phase) with pressure, and comparison with existing experimental results of pure Ce[23], pure Th[24]

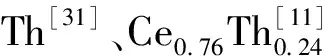
图2 (a)晶格常数a和c随压力变化的规律；(b) 计算得到的bct结构的轴向比(c/a)随压力变化的规律Fig 2 Lattice constants a and c of Ce3Th as functions of pressure and the calculated axial ratio (c/a) of bct phase as functions of pressure

表1 温度为300 K时，0压下Ce3Th合金的平衡体积V0 和体积模量B0

2.2 弹性性质

为了研究立方Ce3Th弹性性质，本文采用了Hooke定律[32]。图3展示了我们所得到的fcc结构的Ce3Th的弹性常数(C11，C44，C12)。在平衡体积下，弹性常数C11、C44和C12分别为60、56.3 和21.7 GPa。满足以下平衡条件，立方晶体在低压下具有力学稳定性[33]：

图3 fcc结构下弹性常数随压力变化的规律Fig 3 Elastic constants as functions of pressure for fcc structure

(1)

对于Ce3Th的fcc相而言,一开始随着压强的增加,所有的弹性常数都呈线性增加。在相变压25 GPa附近，弹性常数C11,C12开始呈现非线性的变化。通过弹性常数Cij，我们还可以计算出体积弹性模量B，剪切模量G。Cij和B，G之间的关系如下[34-36]：

B=(C11+2C12)/3

(2)

G=(GV+GR)/2

(3)

其中，GV=(C11-C12+3C44)/5为voigt剪切模量，GR=[5(C11-C12)]/[4C44+3(C11-C12)]为Reuss剪切模量。

随着压力的增大，C11、C12和弹性模量B呈线性增大趋势明显，而C44随压力的变化程度相对较小。对立方晶体来说，弹性常数C11表示长度弹性，为压缩模量或拉伸模量。C11受纵向应力的影响，使材料晶胞的晶格常数也发生改变，晶胞压缩或膨胀，体积随之发生变化。C12和C44表示形状弹性，为两个剪切或扭转强度模量，其受横向应力的影响，引起材料晶胞剪切或扭转变形，晶胞形状随之发生形变，但不会改变晶胞体积。C11随压力变化程度明显，说明在纵向应力的影响下Ce3Th晶胞压缩或拉伸的程度较大，体积压缩或膨胀较快。C12和C44受横向应力影响，C11变化较明显，而C44变化程度较小，说明引起Ce3Th晶胞扭曲形变的主要剪切模量为C12，而C44对压力不敏感。

图和压力的比值

(4)

图5 bct结构下弹性常数随压力变化的规律Fig 5 Elastic constants as functions of pressure for bct structure

根据Voiget-Reuss-Hill近似，可以通过弹性常数确定理论多晶弹性模量。图6中给出了多晶的平均各向同性体积模量B、剪切模量G和弹性模量E作为压力的函数。随着压力的增加，体积模量B几乎单调增加，剪切模量G和弹性模量E在过渡压力附近发生了明显的“软化”。在图7中可以看到fcc相和bct相的弹性德拜温度都随压力的增加而增加，其中bct相的弹性德拜温度增加的程度最为明显，表明bct结构的Ce3Th在压力下，晶体内部原子振动较为剧烈，相对fcc结构不稳定。且我们能明显地看到在过渡压力附近，线性关系开始“软化”，也进一步说明了相变的发生。此外，我们还研究了晶体内部的弹性声速，数据可通过以下公式获得[37-38]：

图6 体积模量B、剪切模量G和弹性模量E随压力变化的规律Fig 6 Bulk modulus B, shear modulus G and elastic modulus E as functions of pressure

图7 弹性德拜温度随压力变化的规律Fig 7 The elastic Debye temperature as a function of pressure

(5)

如图8所示，其中VP、Vb和VS分别是压缩声速、体积声速和剪切声速。除了声速随压力的增加外，过渡压力周围也有很大的“软化”。该图还给出了Ce的弹性声速(Manganin)和声速(光学方法)。计算结果与Ce在压力35 GPa以下的Vb的实验数据一致。

图8 Ce3Th中声速与压力的关系，以及Ce的声速(光学法)和弹性声速的实验数据[39]Fig 8 Sound velocities in Ce3Th versus pressure together with the experimental data in Cerium[39]

2.3 热学性质

本文利用基于准谐德拜模型的Gibbs程序[40]研究了Ce3Th的热力学性质。通过相应的热力学表达式，就能对材料晶胞的热力学性质进行讨论。如图9，我们在0～1 200 K的温度范围和0～90 GPa的压力范围内研究了Ce3Th的热力学性质。图9(a)显示了不同温度下V/V0随压力变化的规律，图9(b)显示了不同压力下V/V0随温度变化的规律。当V/V0>1，表明原始晶胞扩张，<1表示原始晶胞被压缩，其中V0为零温零压时的Ce3Th晶胞体积。从图9(a)可以看出V/V0随压力的增大而减小，1 200 K时减小的速度最快，表明Ce3Th的晶胞结构随着温度的升高更容易扩展。如图9(a)，300 K时，压强从0 GPa升至30 GPa，fcc相体积减少约29%。压强超过30 GPa后，bct相稳定存在，压强从30 GPa升至90 GPa，体积减少约15%。图9(b)所示，V/V0随温度的升高而减小，高压时减小的速率较为明显，也就是说Ce3Th的晶胞结构在高温高压下容易被压缩，且温度越高，压缩的程度越大。

图9 (a)不同温度下，V/V0随压强变化的规律；(b)不同压强下，V/V0随温度变化的关系。其中V0为零温零压时的体积Fig 9 Value of V/V0 versus pressure P at different temperature and versus temperature T at different pressures, where V0 is the cell volume at P=0 and T=0

在高温下，热容CV趋于Dulong-Petit极限；当温度足够低时，CV与T3成正比[41]。然而，温度CV的变化取决于原子的振动情况，长期以来只能通过实验来确定。图10(a)展示了Ce3Th的fcc相和bct相分别在0、10、20、30 GPa和20、40、60、90 GPa下的CV。随着温度的升高，热容增加，但增加的速度逐渐减慢。由于Debye模型的非谐近似，当T<300 K时，CV随温度升高而急剧增加，当温度升高到400 K时，CV的非谐效应得到抑制，CV逐渐趋于Dulong-Petit极限(CV=49.67 J / (mol·K))，这也是固体在高温下普遍存在的现象。

图10(b)描述了不同压力下Ce3Th热膨胀系数α随温度变化的曲线。显然，在低温下α急剧上升，随着温度升高上升趋势变弱。在一定的温度下，压力越大，fcc相和bct相的热膨胀系数也越大。当P=900 GPa，T>200 K时，α几乎没有变化，说明高压有效抑制了热膨胀。在一定温度下，随着压强P的增大，热膨胀系数α减小。最后，我们预测在0 GPa，300 K的时候，fcc相Ce3Th的热膨胀系数α约为4.27×10-5K-1；在90 GPa，300 K时，bct相Ce3Th的热膨胀系数α约为0.9×10-5K-1。