基于网络流方法的集成电路布线设计
2021-06-07杨尚霖谢龙韬
杨尚霖,谢龙韬
(石河子大学 机械电气工程学院,新疆 石河子832000)
集成电路是利用半导体技术把电子元件集成在一起的具有特定功能的电路,在生活中的多个方面得到广泛运用。集成电路内的电子元件随着技术的高速发展,其内的电子元件数目已高达十亿级别,因此在制作集成电路时需要依靠专业的计算机软件,该类软件统称为电子设计自动化(EDA)工具。制作分为多步骤完成,制作过程中的一大难点是“布线”问题,即在矩形网格中将器件摆放合适之后,利用金属线将其相互连接,但引线之间不能相互交叉避免造成短路。本问题主要研究“布线”中的特例“通道布线”,它是指在一个横向的布线区域,需要连接的方格分布在区域顶部和底部,再利用金属线将其引脚连接起来。
集成电路的通道设计一直是个NP完全问题,由于它的算法时间复杂度高,过去学者对其求解进行过许多研究。20世纪80年代以来,Nobuo Funabiki等[1]人提出了一种并行算法来解决二层通道布线的设计问题;Jens Lienig等[2]人在此基础上,采用遗传近似算法对通道布线问题进行了求解,降低了寻找可行解的时间;随着集成电路的发展,Chen Y K等[3]对二层通道布线方法进行改进,提出了适用于三层通道设计的布线方法;褚静[4】、周晓娜[5]研究了图论在通道布线中的运用;K.Madhavi等[6]、黄训诚[7]、徐宁[8]研究了现代智能算法在通道布线求解问题中的运用。学者们对集成电路通道布线设计求解算法进行了充分的探讨,而对于通道布线问题的数学机理模型的讨论较少。在上述研究的基础上,本文结合网络流理论构建了用于解决集成电路通道布线问题的单目标优化混合整数线性规划模型。运用LINGO求解器对于最为常见的二层通道布线设计问题进行求解。最后结合实例说明了模型的可行性,如图1所示。
1 问题分析
通道布线设计是将对应的引脚用导线相连,在布线的途中不出现串线问题的同时,使布置的导线总电阻值最小为目的的优化问题。对于不同规模的网格,其拓扑结构、引脚位置对求解结果有着十分关键的影响。本节针对网格的结构和连线约束两个方面进行阐述。
1.1 网格结构
(1)网格规模大小直接限制了导线走线,连线不能超出网格。
(2)相邻网格和网格之间才能用导线连接。
1.2 连线约束
(1)对应各个引脚必须用导线连接。
(2)一层通道内,每个网格只能有一条导线经过,否则存在串线问题。
(3)导线在穿过两层通道之间时,需在中间安置通孔,通孔对电路电阻有影响。
2 数学模型建立
2.1 符号含义说明
集成电路通道布线设计是将对应的引脚通过矩形网格用导线相连,寻找连线总电阻值最小的优化问题。为了解决此问题,首先需对一些符号进行定义说明,见表1所示。

表1



2.2 目标函数与约束条件

上述模型中,目标函数式表示的是布线总路径电阻值最小;约束条件反应的是:(2)式要求每条导线的连接是连续的;(3)式表示的是每条线只能经过一个网格一次;(4)(5)式表示的是第1、2层的每个网格最多只能由一条导线经过;(6)式表示通孔的存在条件;(7)式表示每条线的对应引脚起点和终点必须相连;(8)(9)式表示只能用导线连接相邻的网格;(10)(11)式表示决策变量均为0-1变量。
3 结果分析
通过将不同规模大小、不同引脚个数的集成电路代入模型进行布线设计,通过LINGO求解,分析模型结果的可行性,见表2、图2所示。
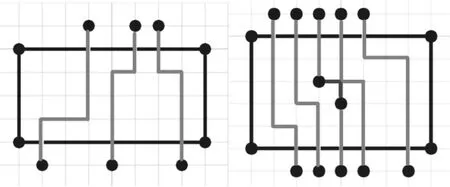
图2 通过LINGO求解得到的布线效果图
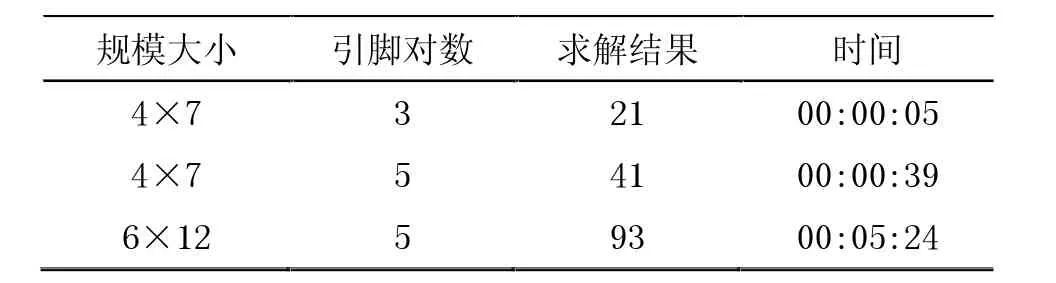
表2 算例求解结果
4 结论
本文针对集成电路通道布线问题进行研究,以布线电阻值为布线主要因素,考虑到布线长度以及通孔个数对于线路电阻值的影响,建立设计了一个以线路电阻值最小为优化目标的数学模型,通过将模型代入LINGO求解得到的结果,可以大大降低布线电阻值,提高了布线电路的性能和可靠性。
本文未考虑线路弯曲对于线路电阻值的影响,线路电阻会由于线路的弯曲而变化,它对电路性能有着很大影响。
