一道全国联赛福建赛区预赛题的探究

福建省莆田第五中学 (351100) 黄洪飞

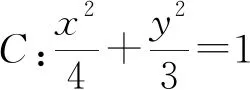
图1

1．探究一般性结论

上述结论揭示了特殊的椭圆C的右焦点和右准线的一个关联性质，那么，对于一般的椭圆，是否具有这一性质？经探究，可得：

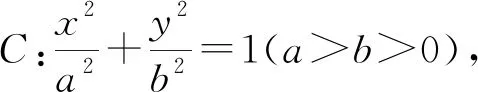
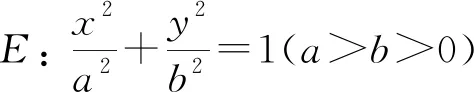
图2

类似地，容易得到双曲线、抛物线的相应结论.

结论3 已知抛物线C：y2=2px(p>0),过准线上一点P作抛物线C的切线PA,PB,A,B为切点，F为焦点，则A,F,B三点共线，且PF⊥AB.

2.探究结论的逆命题

上述结论揭示了圆锥曲线的准线与相应焦点的一个关联性质，那么，其逆命题成立吗？即若点P在准线上，A,B在曲线C上，若A,F,B三点共线且PF⊥AB，那么直线PA,PB是否是曲线C的切线？经探究，有如下结果：

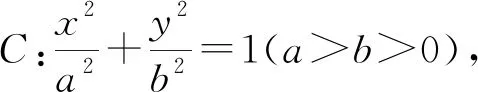
类似地，可得双曲线、抛物线的相应结论：

结论6 已知抛物线C：y2=2px(p>0),点P在准线上，A,B在抛物线C上，F为焦点，若A,F,B三点共线且PF⊥AB，则直线PA,PB是抛物线C的切线.

下面只证明结论6，结论5可仿照结论4的证明证之.

3.探究结论的拓展

由结论1、2、3的条件，是否还可以得出其他结论？经探究，可得：

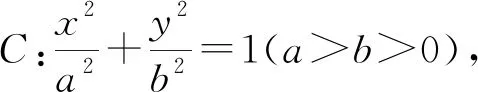
综上，有OP平分线段AB.

由结论1及7可得：

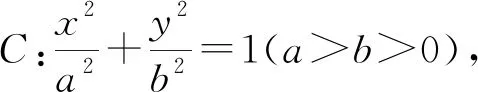
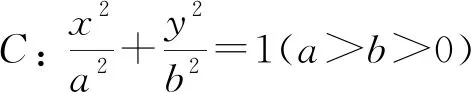
类似地，可得双曲线,抛物线的相应结论：

结论9 已知抛物线C：y2=2px(p>0),过准线上一点P作抛物线C的切线PA,PB,A,B为切点，则过点P且平行于x轴(或在x轴上)的直线平分线段AB.

推论3 已知抛物线C：y2=2px(p>0),点P在准线上，A,B在抛物线C上，F为焦点，若A,F,B三点共线且PF⊥AB，则 过点P且平行于x轴(或在x轴上)的直线平分线段AB.

下面只证明结论9，结论8可仿照结论7的证明证之.

综上，结论9得证.

以上对一道预赛试题的探究，得到了关于椭圆、双曲线和抛物线的一系列结论.对于一些典型的试题，我们不仅要研究试题的解法，还要引导学生探究试题理论背景，发掘试题的内涵，发现新的规律和结论.这样，才能领会到试题的深刻背景，才能引领学生跳出题海，做到触类旁通、举一反三，从而培育和提升学生的数学学科核心素养.