2021年八省模考数学解几压轴题的解法探究

广东省中山市濠头中学 (528437) 张 宇

1.试题呈现

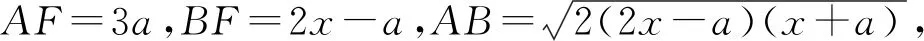
2.解法探究

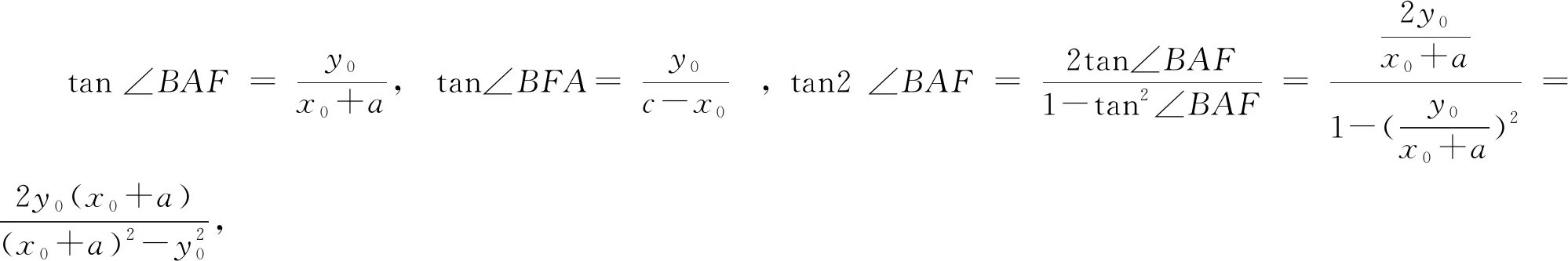
评注：此证明用正切函数折定义，然后由正切函数的二倍角公式，思路清晰，是绝大多数学生所采用的方法.

(1)当BF⊥AF时，结论显然成立.

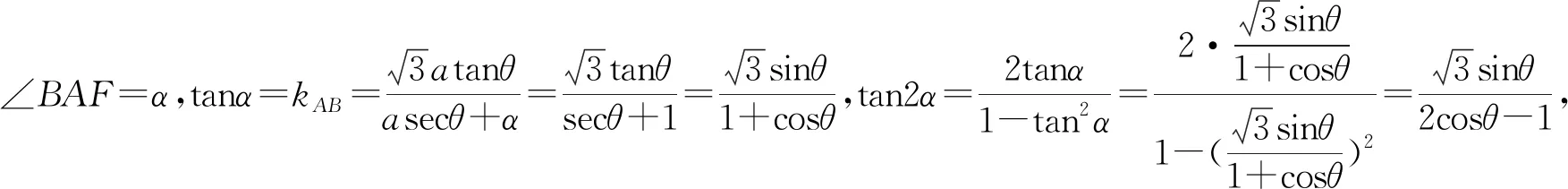
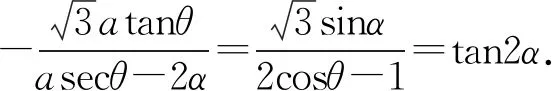
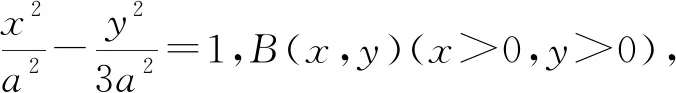
评注：这里从斜率入手进行证明，本质上和证法1没有太大的差别，思路比较清晰，很多学生采用了这种证明方法.

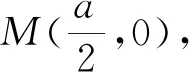
评注：运用角平分线上的点到两边的距离相等进行证明，还用到了垂直平分线的知识.这种证明初中学生都能理解.同时用到了点到直线的距离公式，是一种不错的证明方法.

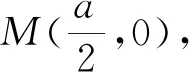
评注：运用余弦定理验证cos∠BAM=cos∠BMN，对学生的运算能力要求较高，不过和以前的解析几何压轴题的运算量相比，这个就显得特别简单了.

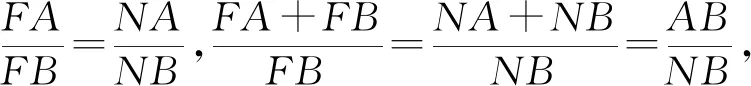
评注：用初中的角平分线性质定理进行证明，初中学生都可以理解，作为高考模拟题中的压轴题，有点名不符实，现在初中对平面几何要求较低，这是一件比较遗憾的事.对培养学生的逻辑思维能力造成一些不利影响.

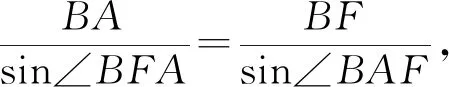
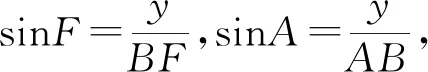
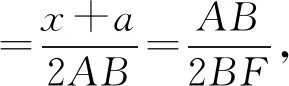
评注：回归到本质的定义中去，用正弦的二倍角公式，也是容易想到的方法，作为有现成结论的问题.教师在教学中加强对学生进行发散思维的训练，进行一题多解是不错的选择.

3.试题探源

此题的原形在以前的竞赛及自主招生试题中多次出现.试题原形在2010年福建高中数学预赛试题和2014年甘肃高中数学竞赛预赛试题中两次出现.另一原形题在2011年华约自主招生试题的第13题出现.

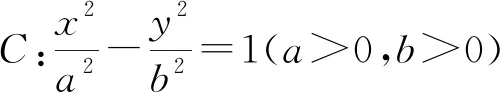
(1)求双曲线的方程；

(2)设Q为双曲线C右支上动点，F为双曲线右焦点，在x轴负半轴上是否存在定点M,使得∠QFM=2∠QMF？若存在，求出点M的坐标；若不存在，请说明理由.

2014年甘肃高中数学竞赛预赛的第13题采用了此题，在文字上没作任何变动.江苏省著名特级教师蔡玉书老师在《解析几何竞赛读本》第二章(中国科技大学出版社出版)中选用了此题作为例题.

(1)求C的离心率；

(2)设A为C的左顶点，Q为第一象限内C上的任意一点，问是否存在常数λ(λ>0)，使得∠QF2A=λ∠QAF2恒成立.若存在，求出λ的值；若不存在，请说明理由.

此问题还可进行如下变式：

4.结语

解析几何大题一直以来以压轴题的形式出现在高考试题或模拟试题中，但这次的解析几何试题的难度并不大.更大程度上这是一道解三角形的问题，知道三角形的三条边，求三角形的两个角.并且这次模拟题的计算量较小.

作为解析几何压轴题，在以前的高考试题中，绝大多数时为椭圆，然后是抛物线，双曲线相对考得较少.传统圆锥曲线压轴题的解法主要采用到直线与圆锥曲线的交点及通过解方程组，然后由韦达定理等.

双曲线在新课标中属于了解范围，一般不出大题，这次虽在第21题出了双曲线大题，但设问方式比较常规，重点还是考查学生数学运算等核心素养，以及转化化归等数学思想.教师在以后的教学及复习中力求做到以下几点：

(1)构建牢固的知识网络：高考复习中，一定要加强基础知识、基本技能和基本数学思想方法.抓住各部分知识之间的联系和综合，形成知识之间的纵横联系的网络，达到“牵一发而动全身”的境界.

(2)提高解题的各种能力：在教学中选出最优秀的试题，最具典型性和最有价值的试题，讲题时渗透数学基本思想，让学生理解数学知识的本质，形成对知识的悟性，提高他们的数学思维品质及分析问题与解决问题的能力.

(3)转变教学观念：重视数学思想方法的渗透和运用，要始终坚持指导学生自己进行数学思想和方法的提炼，让学生从思想上去揭示问题的本质.在解题后进行反思和提炼是成功的经验.发挥学生的主观能动性和教师的主导地位.