借助外接圆模型解决一类解三角形的最值问题

山东省滨州市邹平县黄山中学 (256200) 韩景岗

广东省佛山市顺德区容山中学 (528303) 潘敬贞

广东省汕头市澄海华侨中学 (515800) 张应楷

在解三角形问题中，经常会遇到一类定长对定角的三角形(或是四边形)求其边长或面积的最大值问题.解决此类问题的一般方法主要是综合运用正弦定理与余弦定理实现边角互化，结合三角形内角和定理，利用三角函数的单调性求最值.这样做，过程往往比较复杂冗长，如能用好给定三角形的外接圆并结合其几何性质来处理，问题解决往往事半功倍，既能有效减少运算量，也能够将抽象的问题直观化，复杂的问题简单化.文章结合具体实例谈外接圆在解三角形最值问题中的实际运用，形成一类解三角形最值问题的模式化解题方法.

一、三角形周长的最值问题

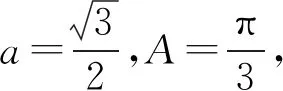
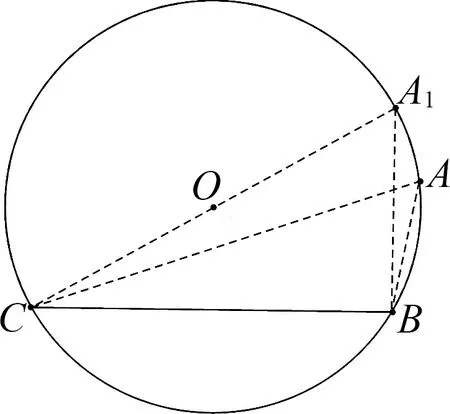
图1

评注：本题如果采用常规的代数运算，需要利用正弦定理进行边化角，然后进行三角恒等变换，最后通过确定角的范围利用三角函数的单调性求出其范围；但是过程较复杂，并且对运算能力要求较高；也可以利用余弦定理与基本不等式得到一个最值，但是另一个临界值比较难得到.如果能根据已知条件确定三角形的外接圆，便可通过直观观察外接圆上动点A的变化规律找到临界位置，从而得出结果.

图2

评注：借助外接圆突出几何直观，可以有效避免复杂的代数运算与逻辑推理过程，既体现了数形结合的思想，又能在问题解决的过程中发展学生的数学建模与直观想象核心素养.

二、三角形面积的最值问题

例2 (2014课标Ⅰ卷理16)已知a,b,c分别为△ABC三个内角A，B，C的对边，a=2，且(2+b)(sinA-sinB)=(c-b)sinC，则△ABC面积的最大值为．

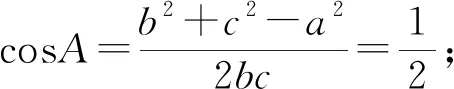
图3

评注：本题如果用常规解法，需要利用正弦定理或是余弦定理，过程会显得冗长，但采用三角形外接圆求解时，会瞬间得到答案，省去了太多的时间，达到了省时省力的效果，也体现了小题小做的特点.

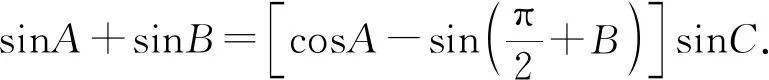
解析：(1)由已知得sinA+sinB=(cosA-cosB)·sinC，分别利用正弦定理与余弦定理实现角化边得a+b=

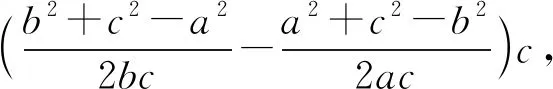
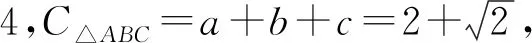
评注：若本题能够基于问题(1)的结论作出三角形的外接圆如图4所示，结合直角三角形的性质可知当且仅当三角形为等腰直角三角形时面积最大，从而快速得出答案，足以见出外接圆在解决三角形面积最值问题中具有重要的应用价值.

图4

三、四边形中边长的最值问题

例3 (2015新课标Ⅰ卷理16)在平面四边形ABCD中，∠A=∠B=∠C=75°，BC=2，则AB的取值范围是.

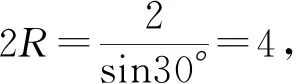
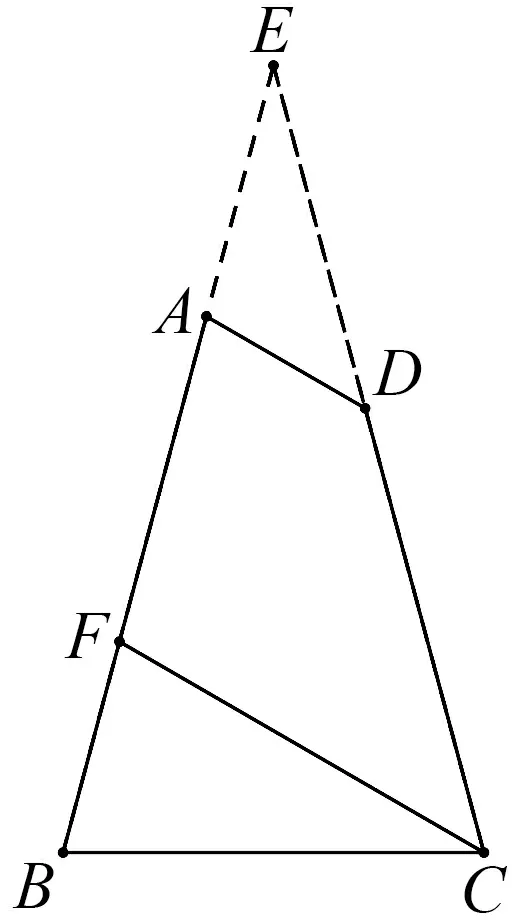
图5

评注：这是一道难度不小的高考压轴小题，如果利用常规的正余弦定理求解，过程繁琐且不宜操作，但是利用三角形的外接圆模型，可以快速找到问题的突破口，充分展现了极限思想，突出数形结合.

图6

评注：解答该题的关键点是根据对角互补从而联想到四边形的外接圆，通过点的位置移动直观观察CD的取值范围，直观明了.

四、四边形中面积最值问题

图7

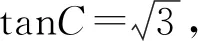
评注：该题是一道比较常规的采用二元变量转换为一元变量的题目，解题过程比较复杂，且对于一些基础相对薄弱的学生很难完成对该题的正确解答；但是如果借助三角形的外接圆模型来处理，问题就会变得很简单，通过观察点的变化特点可以直接找出边的取值范围.

变式已知在△ABC中，BC=2，以AC为边做一个等边三角形，点C、D在AB的同侧，则△ABD面积的最大值为.

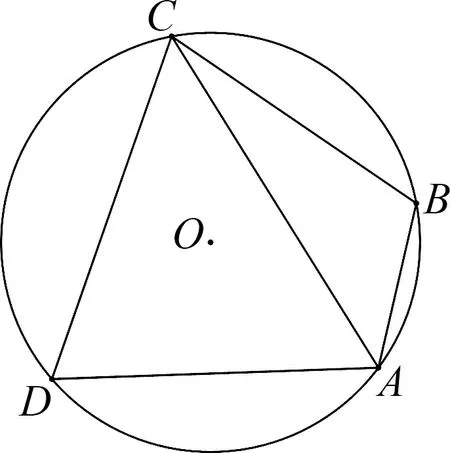
图8

评注：该题是一道典型的动态问题，如果用常规的解析法来处理难度很大，由于该题又是一道填空题，所以可以借助外接圆直观找到取最值的情况，这充分体现了外接圆模型在解决三角形与四边形问题中的重要意义.

数缺形时少直观，形缺数时难入微，这是数形结合思想的重要意义.数学的学习过程关键在于悟，要学会感悟知识的发生与发展过程，体会知识间的逻辑联系，构建数学知识体系，最终达到能综合运用所学知识高效解决实际问题的目的.这也正是新课标中要学会用数学的眼光观察世界，用数学的思维思考世界的具体要求.以形助数，以数辅形是数学知识的本质属性，学会挖掘变化的问题背后所隐藏的不变的数学本质是数学学习的重要任务.这不仅可以提高解题效率，更重要的是能够更好的发展数学核心素养，优化数学思维，形成适应社会发展所必需的的关键能力和必备品格.