例谈求解向量数量积问题的四种策略

江苏省苏州工业园区教师发展中心 (215021) 杨原明

向量数量积的运算是向量问题中的一个重要内容，经常与平面向量的模与夹角等知识交汇，表现出的题型也多种多样，如求值、求最值、求参数范围等．但有些学生由于各类题型缺乏科学的训练和系统地整理，遇到此类问题还是显得束手无策，本文介绍常用的四种方法，旨在帮助归纳整理，仅供参考．

1.提取合并：就是在给出的向量数量积条件式中，反用向量相乘的分配律，通过先部分提取向量，然后构造出新的向量数量积的形式达到转化问题、解决问题的目的．

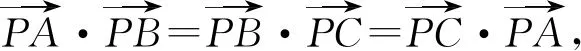
A．外心 B．内心 C．重心 D．垂心

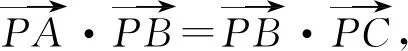
评注：由于向量运算满足乘法的交换率，故在处理数量积问题时，经常使用提取的手段转化问题，本题中通过对所给等式中采取移项、提取相同的向量，展示出了向量间的几何特征，为后面的判断提供了强力的支持．

评注：由于题目中的条件单一，怎样用好这个条件是解题关键，而向量的数量积关系向三角形边之间关系转化就是如何得到向量平方之间的关系，其中的提取法是一个重要解题方法．

2.分解变形：在解决向量求积问题时，利用向量的加、减法法则对所给向量式进行拆分、分解、重组等转化，使之变形到能够利用已知条件解题为目的．

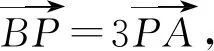
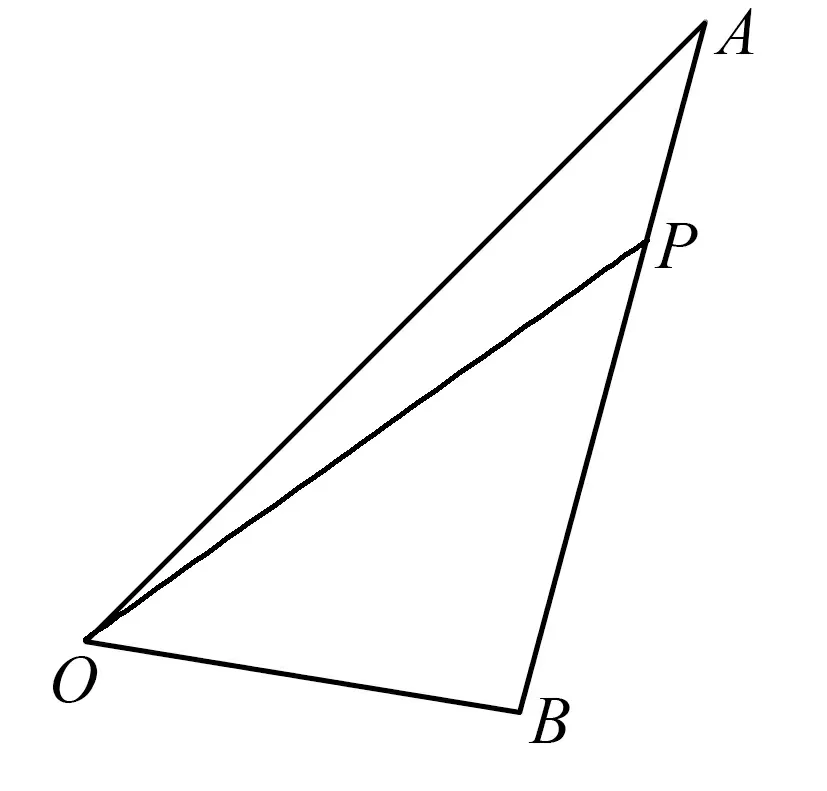
图1

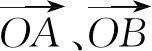
评注：在分解向量时要有目标意识，其目的是有利于运用已知的向量模和夹角等条件来解题，本题中正确的使用题设向量表示所求结论中的向量是解题关键．

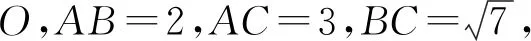
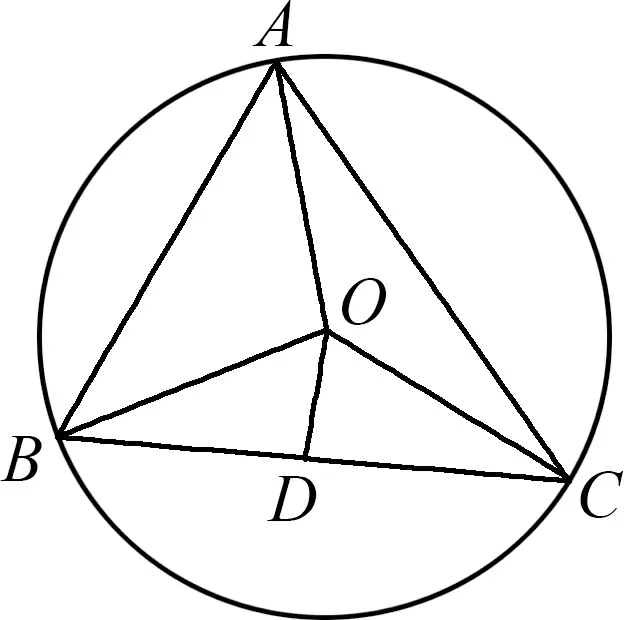
图2

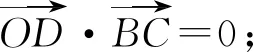
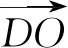
3.引参转化：在求与向量数量积的最值问题时，可以通过引入参数，将一些变化中的向量表示出来，再用代数中求最值的方法解决问题．

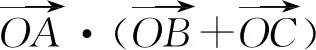
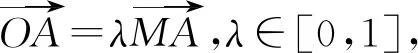
评注：如果一个动向量是在已知的向量上移动，可灵活运用共线向量的定理，引入参数，将动向量用已知向量表示出来，将动向量问题通过已知向量替换转化，就容易达到解题目的了．

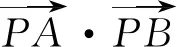
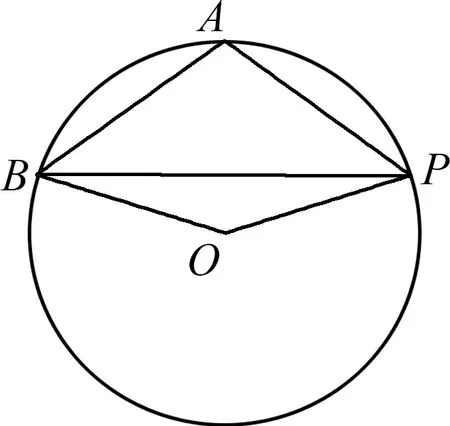
图3

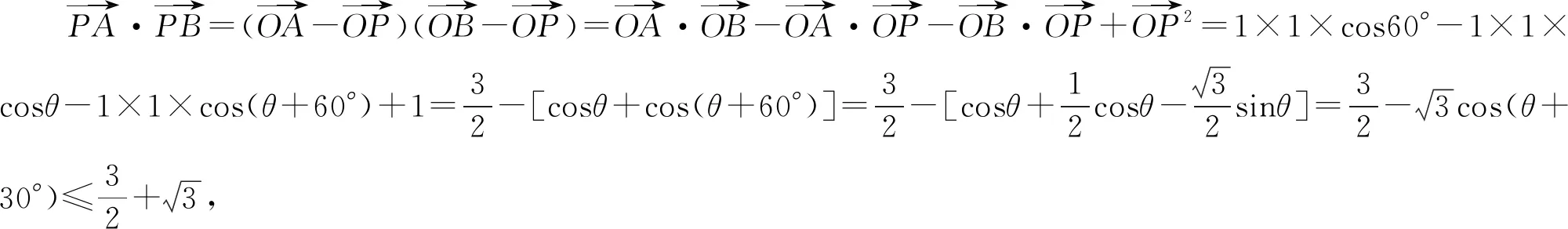
评注：对于圆(或弧)上的动向量问题，通过设角为参数，就可以将动向量与已知的向量建立联系，然后再抓住圆心及圆的相关性质转化待求的向量数量积，最后利用三角函数的性质解决最值问题．

4.两边平方：解决向量模的问题的一个重要方法就是平方运算，同样在一些向量数量积问题中，通过对相关向量式进行两边平方也可以得到向量的数量积关系式，这样就为成功解题创造了条件．

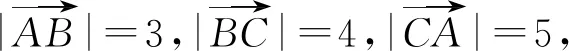
评注：本题通过认真研究题目所给的条件和待求的结论，发现了结论式其实可以由一个三项式的平方得到，这就是审题的效果．高瞻远瞩，把握问题的实质，然后用整体平方求解，圆满高效的完成答题任务．此题还可以挖掘出△ABC是直角三角形，再利用其特点来解题．

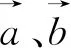
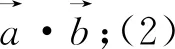
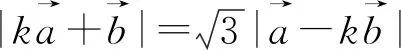
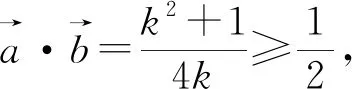
评注：由于给出的条件是向量模的等式，且要求的向量数量积是包含在模的等式中，故而求解此题的最好方法就是两边平方．而后面的抓住k>0，运用基本不等式求最值就是一些水到渠成、垂手可得的操作了．

以上展示了解决向量数量积问题的四种常用方法和运用技巧，但平时解题中还应该需要运用到其它方法帮助解题，并且注重精做精练，不断总结归纳，增加知识储备，只有这样，我们的解题能力、思维品质才会有较大的提升．