例谈判别式法求最值问题的类型与技巧

浙江省东阳中学 (322100) 史静晓

在一些已知等式求某个代数式的最值的问题中，如果通过变形能够得到关于某个实变量的二次方程或二次不等式时，此时运用判别式法求最值也是一个比较好选择，下面举例分析几个常见题型，旨在探索解题方法与技巧，供读者朋友参考．

一、模型化归

通过代数变形，将函数式转化为一个含参数的二次方程，可抓住方程有解的条件即根的判别式大于或等于零建立不等式，求出此函数最大值和最小值．

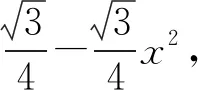
评注：通过对所得函数模型的分析思考，成功的将目标函数式转化为一个一元二次方程，再由判别式得到一个关于参数t的不等式，求出t范围，从而面积S的最小值．

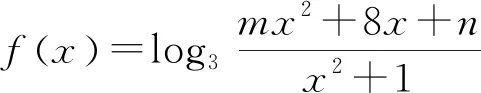
评注：将二次分式函数转化为一元二次方程后，为应用判别式法求出函数的最大值和最小值创造了条件，这是解题关键，此法也是求二次分式函数值域的重要方法．

二、消元转化

在含有多个变元的等式中，通过等式的转化消去一些变元，然后再利用转化后的一元二次方程的根的判别式解决求最值问题．

例3 已知实数x，y，z满足x+y+z=0，x2+y2+z2=1，则z的最大值是．

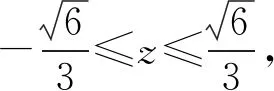
评注：本题中有两个已知等式，三个实变量，消元是首要任务，这样也就顺利转化为二次方程有实数解的问题了．

例4 设x，y，z都是实数且满足条件x+y+z=0和xyz=2，求|x|+|y|+|z|的最小值．

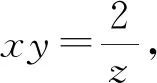
评注：在利用判别式法求最大值或最小值时，要注意等号条件的分析，一般都是判别式等于零时取得，必须清楚这一点．

三、换元变形

如果题目中含有二次等式条件的，这是运用判别式法求解的一个典型信号，而换元处理是变隐为显的有效措施．

例5 设x,y为实数，若4x2+y2+xy=1，则2x+y的最大值为．

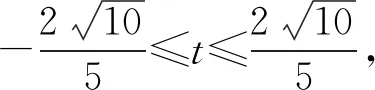
评注：通过将欲求的表达式换元后代入已给等式，得到了一个关于x的一元二次方程，再由判别式列出不等式使问题得到圆满的解决．

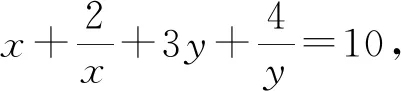
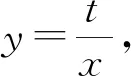
评注：由于题设所给等式的结构比较复杂，最后得到的不等式也有些麻烦，但是只要方法正确，方向明确，处理得当，就能顺利完成解题目标．

四、灵活构造

若条件比较隐晦，比较难发现破题的方法，则可以通过构造创造出一元二次方程，达到了运用判别式解题的前提条件．

例7 已知a,b∈R，a2+ab+b2=3，设a2-ab+b2的最小值和最大值分别是N、M，则M+N=．

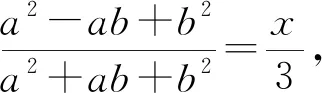
注评：本题换元起不到减元化简的效果，因此不能直接代入，通过重新构造并再一次换元，终于得到了所需的一元二次方程，为后面运用判别式解题创造了必须的条件．

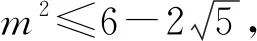
评注：本题是隐含的二次不等式恒成立问题，根据二次不等式的特点，通过不断构造出判别式来帮助解题，虽然过程复杂繁琐，只要有目标、有信心就能使问题获得解决．