考虑不同管片拼装方式的超大直径盾构隧道衬砌受力变形分析

范一鸣，李博，刘波

（1.亳州职业技术学院，亳州 236800；2.亳州市重点工程建设管理局，亳州 237800；3.东南大学 土木工程学院，南京 210098)

近年来，盾构法在我国隧道工程建设中发挥了重要作用。盾构法隧道由多块管片经螺栓拼装组合而成，以抵御周围水土压力和其他荷载。盾构隧道的受力变形受到拼装方式、地层条件等诸多因素的影响。

目前，对盾构隧道衬砌的研究方法主要有数值模拟、现场和室内试验以及理论分析。例如，郭瑞等采用非线性有限元方法分析了地层抗力系数、地层侧压力系数、管片接头抗弯刚度以及管片拼装方式对隧道稳定性的影响，并与失稳破坏相似模型试验结果进行了比较。陈俊生采用三维有限元法建立了一个具有9 环管片的盾构隧道数值模型，通过施加与施工阶段相应的注浆压力、千斤顶顶力以及盾尾刷挤压作用，分析了施工阶段管片的变形特点及应力分布；封坤等采用自行开发的“多功能盾构隧道结构体试验系统”，以南京长江隧道工程为依托研究了通缝和错缝两种拼装方式下管片的不同破坏特征。王士民对以深港狮子洋隧道为原型，采用模型试验的方法对极端荷载条件下水下盾构隧道衬砌结构破坏过程进行了探讨。杨雨冰等采用基于断裂力学的有限元法，从单块管片、2 块管片（含接头）、整环衬砌结构3 个层次探讨了盾构隧道管片的破坏机制，指出管片接头的模拟是准确预测整环衬砌结构极限承载力和变形性能的关键。杨林德等和刘四进等分别研究了水下盾构隧道管片混凝土中氯离子的运移规律，揭示了裂缝深度与钢筋锈蚀时间的关系。黄宏伟等、叶飞等通过模型实验法分别研究了通缝和错缝拼装方式下盾构隧道的横向和纵向刚度有效率。上述研究对科学认识盾构隧道性能演化、优化衬砌结构设计发挥了积极作用。然而，目前关于超大直径盾构隧道的研究，尤其是管片结构在复杂荷载环境下受力变形的研究仍相当有限，且一些研究中对于管片接头的处理方式仍存在较大争议。

本文在前人的基础上，以扬州瘦西湖超大直径盾构隧道为背景，采用有限元法建立能够考虑衬砌块与块、环与环、衬砌与周围土体相互作用的有限元计算模型，采用荷载结构法计算了错缝和通缝两种拼装方式下隧道衬砌内力和变形，分析了不同拼装方式的影响，以期研究结果能为超大直径盾构隧道衬砌优化设计提供参考。

1 工程概况

1.1 工程简介

扬州瘦西湖隧道位于国家5A 级风景名胜区-瘦西湖风景区内，呈东西走向，隧道主要由东、西明挖段和中间盾构段组成。其中盾构段是我国当前直径最大的单管双层盾构隧道，也是国内第一座穿越国家5A 级旅游景区的水下隧道。隧道为双向4车道，上下双层布置，上层隧道通行由东向西车辆，下层隧道通行由西向东车辆，如图1 所示。

图1 扬州瘦西湖隧道单管双层结构示意图

1.2 工程地质与水位地质条件

根据现场和室内土工试验，勘探深度范围内的土体从上向下依次为：①杂填土，厚约0.5～4.4 m；②-1 粉土，厚约1.2～2.2 m；②-2 粉砂，厚约1.85～6.8 m；③-1 粘土，厚约42.1～48 m；下伏基岩为全风化～强风化泥质粉砂岩，全风化厚约1～9.9 m，强风化厚约1～4.6 m，土层物理力学参数指标见表1。盾构隧道主要位于粘土层中，隧道拱顶距地表最大埋深约24 m，如图2 所示。

场地地下水主要为第四系松散岩类孔隙潜水，主要分布于①填土、②-1 粉土、②-2 粉砂层中，潜水位平均埋深-3.5 m。

表1 土体主要物理力学参数

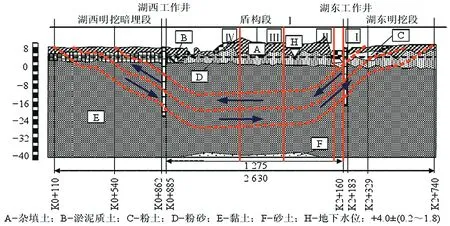
图2 隧道纵断面示意图[12-13]

1.3 隧道管片设计参数

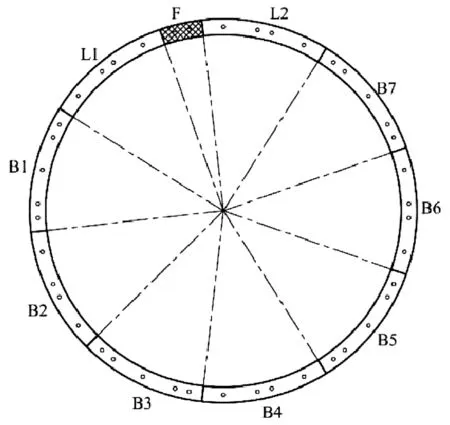
图3 瘦西湖隧道管片拼装示意图

本隧道外径14.5 m，内径13.3 m，管片厚度0.6 m，幅宽2.0 m，每一环由封顶块（F）、邻接块（L1）、邻接块（L2）以及标准块（B1～B7）共十块组成。管片材料采用C60 混凝土，抗渗等级P12，钢筋采用HPB300 和HRB400 级钢。封顶块圆心角为12°51′25.7″，邻接块与标准块圆心角相等，均为38°34′17.14″，管片结构如图3 所示。

2 数值模拟研究

2.1 模拟方案

盾构法隧道衬砌是由若干管片通过环向螺栓和纵向螺栓组合拼装而成，管片的拼装方式有错缝和通缝两种。相邻两环间纵缝相互错开的情况称之为错缝拼装，如图4（a）所示；所有衬砌环的纵缝呈一条直线没有角度错动的情况称之为通缝拼装，如图4（b）所示。不同管片拼装方式下隧道受力变形将有所不同。

为了分析管片拼装方式对瘦西湖隧道这种超大断面隧道结构受力变形性能的影响，本文拟对错缝和通缝拼装两种方式下的隧道结构进行建模研究。错缝拼装由于纵缝不在一条直线上，因此环与环之间相当于存在一定的旋转角度。以图3所示的状态为初始位置，扬州瘦西湖隧道分别顺时针旋转25°42′51.4″、102°51′25.7″、180°、257°8′34.3″、334°17′8.6″，每六环形成一个循环单元，直至拼装完整个隧道。通缝拼装由于纵缝在一条线上，环与环之间不需要旋转角度，以图3 所示的状态为初始位置，始终沿同一角度拼装，直至拼装完整个隧道。

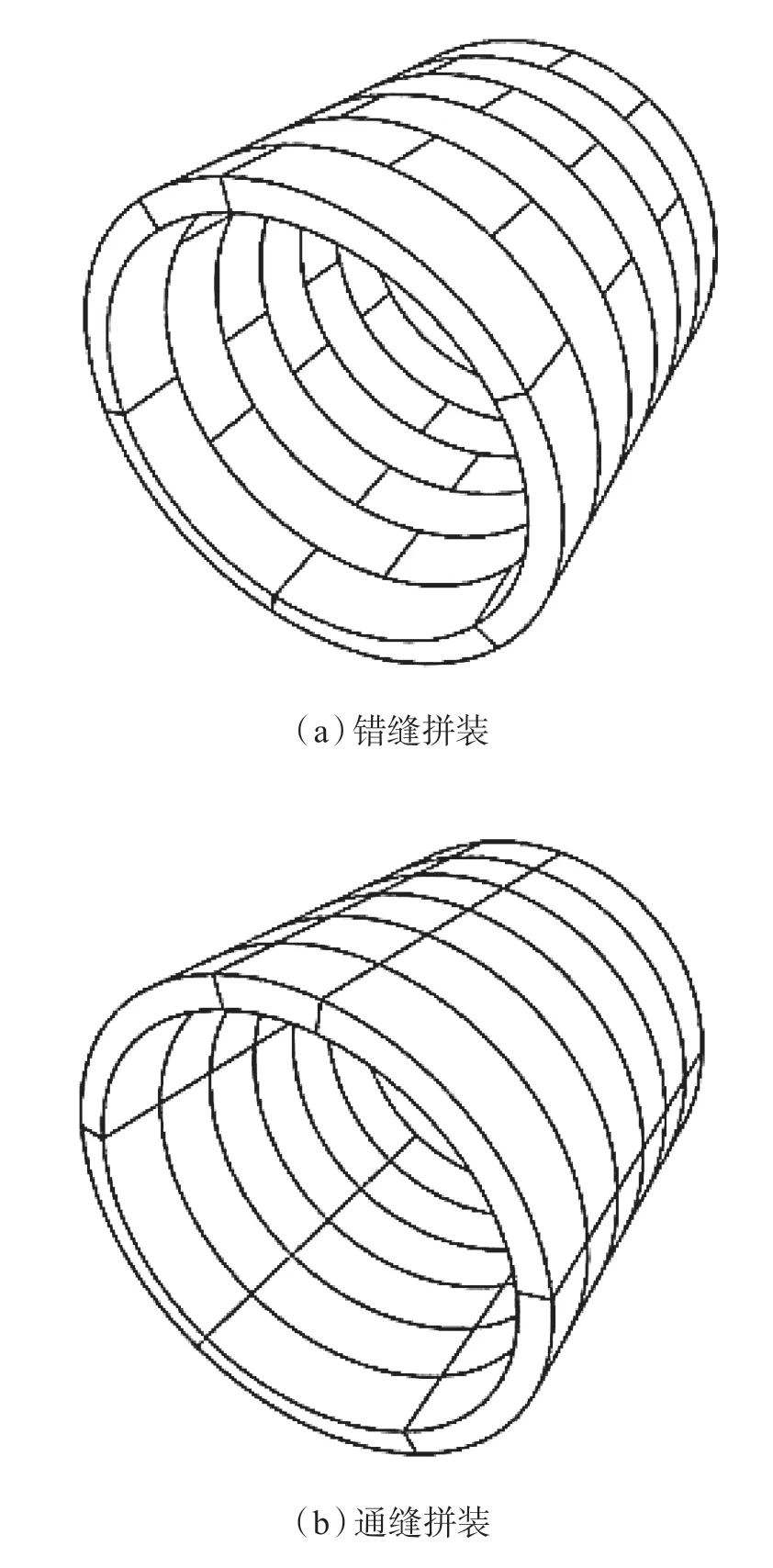
图4 盾构隧道管片拼装方式示意图

2.2 隧道计算模型

根据管片接头处理方法的不同，隧道的计算模型主要有均质圆环模型（惯用法）、等效刚度圆环模型（修正惯用法）、自由铰圆环模型、弹性铰圆环模型。弹性铰圆环模型也可称为“梁-弹簧模型”，即将管片结构视为梁，将管片之间的接头视为变形连续的弹簧，通过梁和弹簧这两个力学元件模拟管片和接头的力学特性。本文将管片作为计算上较为简单的直梁单元考虑；采用旋转弹簧来模拟管片块与块之间螺栓的实际效应；采用剪切弹簧来模拟管片环与环之间螺栓的实际效应；同时将地层与管片之间的相互作用用仅受压地弹簧来模拟，如图5 所示。

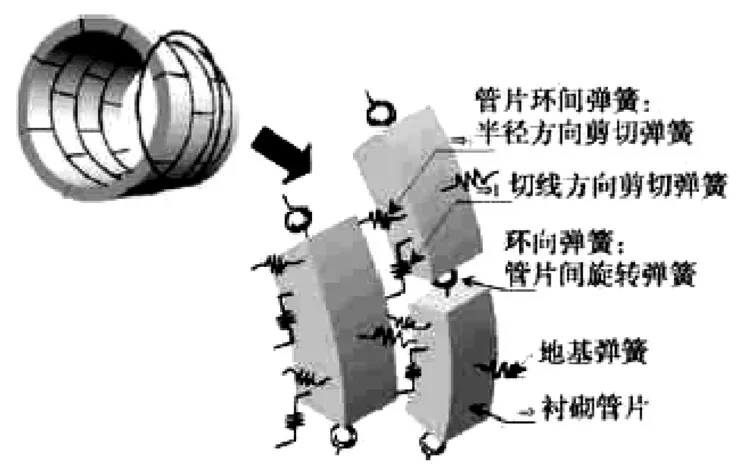
图5 梁-弹簧模型原理示意图[18]

2.3 模型建立

本文采用荷载结构法对隧道结构进行线性静力分析。错缝拼装方式下，采用梁单元模拟隧道管片，管片与管片之间存在一定缝隙，采用弹簧模拟管片块与块之间、环与环之间以及管片与地层之间的接触关系，建立好的盾构隧道计算模型如图6（a）所示。通缝拼装方式下所采用的模拟单元与错缝方式下的一致，结构计算模型分别如图6（b）所示。

错缝拼装时，把图3 所示位置的衬砌环称为环1，把初始环顺时针旋转334°17′8.6″后的管片称为环6。模型约束环1 和环6 的Y 方向位移。错缝拼装和通缝拼装方式的地基弹簧长度均取1 m，弹簧末端约束X、Y、Z 三个方向位移。

2.4 模拟参数

管片材料采用线弹性本构模型，单位重度γ=26 kN/m，弹性模量E=3.6×10MPa，泊松比ν=0.2。结构模型中要特别说明的是弹簧模量的考虑方法。管片接头弹簧的刚度特性，其基本参数见表2。

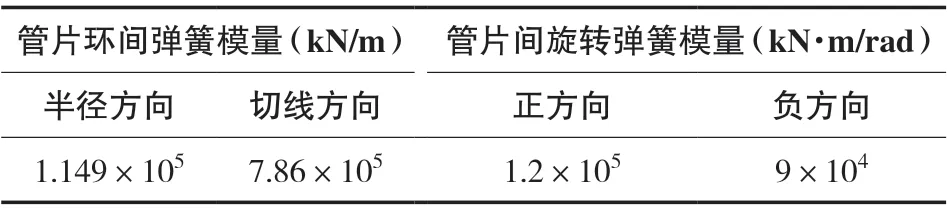
表2 管片接头弹簧基本参数

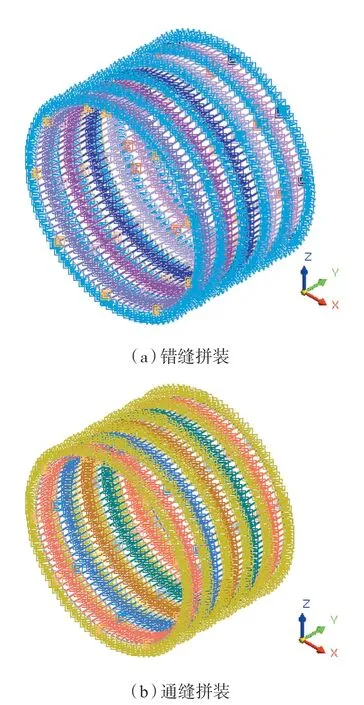
图6 不同管片拼装方式盾构隧道计算模型

荷载结构法中，一般将作用于衬砌上的荷载按表3 进行分类，主要包括主荷载、次荷载以及特殊荷载。本文仅考虑主荷载对衬砌结构的影响，如图7 所示，土压力通过竖直和水平两个方向施加在衬砌上，水压力垂直施加在衬砌表面。荷载计算时采用水土分算。

图7 隧道衬砌受力示意图

表3 盾构隧道设计荷载分类[19-20]

结合图8 所示的隧道埋深示意图，管片所受各荷载分别计算如下：

由于隧道埋深小于2 倍等效荷载高度，属浅埋隧道，因此隧道拱顶竖向土压力未采用松动土压力而采用全覆土压力计算：

隧道拱顶水平土压力：

隧道拱底水平土压力：

隧道拱顶水压力：

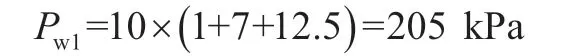
隧道拱底水压力：

拱底自重反力主要由下半环承受，自重反力：

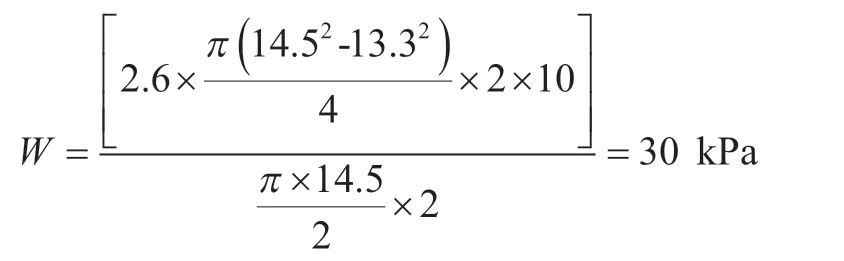
隧道地基抗力：

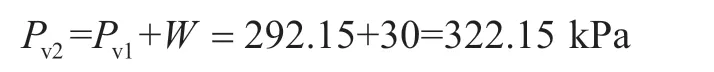
图8 隧道埋深示意图

3 模拟结果分析

3.1 位移分析

位移输出结果的方向以图6 中所示的整体坐标系为准。图9 为错缝和通缝拼装方式下隧道衬砌X 方向水平位移云图。可见，通缝拼装方式下衬砌水平位移延隧道轴向的分布比错缝拼装方式下的更加均匀。错缝拼装方式下，衬砌向隧道内部最大水平位移14.83 mm，位于环5 上。通缝拼装方式下，衬砌向隧道内部最大水平位移16.51 mm，位于环1 上。错缝拼装方式下X 方向最大水平位移比通缝拼装方式下减少约11.5%。

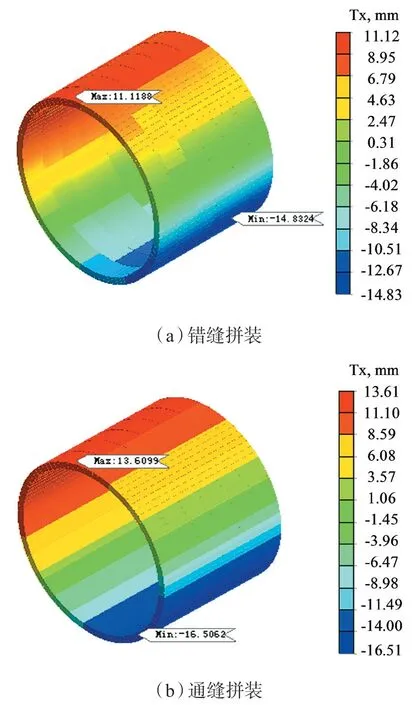
图9 不同管片拼装方式衬砌水平位移云图

图10 为错缝和通缝拼装方式下隧道衬砌Z 方向竖直位移云图。同样可见，通缝拼装方式下衬砌竖向位移延隧道轴向的分布比错缝拼装方式下的更加均匀。错缝拼装方式下，衬砌向下最大沉降23.83 mm，位于环3 上。通缝拼装方式下，衬砌向下最大沉降30.43 mm，位于环1 上。错缝拼装方式下Z 方向最大竖向位移减少约27.7%。

图10 不同管片拼装方式衬砌竖直位移云图

图11 为错缝和通缝拼装方式下隧道衬砌的角变形云图。可见，错缝拼装方式下，随着管环的旋转，角变形分布延轴向出现差异，每一衬砌环的最大角变形位置均不同，衬砌最大角变形2.42×10rad，出现在环5 上。通缝拼装方式下，衬砌角变形延轴向的分布比较均匀，最大角变形3.06×10rad，出现在环1 上。错缝拼装方式下最大角变形较通缝拼装减小约26.4%。

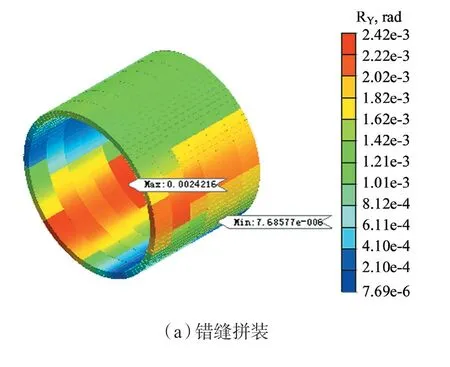
图11 不同管片拼装方式衬砌角变形云图

3.2 应力分析

有限元计算程序中1D 单元的应力输出结果的方向以单元坐标系为准，因此在建模时对单元的方向进行了统一，如图12 所示，图中红色箭头代表X 方向（环向），绿色箭头代表Y 方向（纵向），蓝色箭头代表Z 方向（径向）。

图12 1D 单元坐标系统

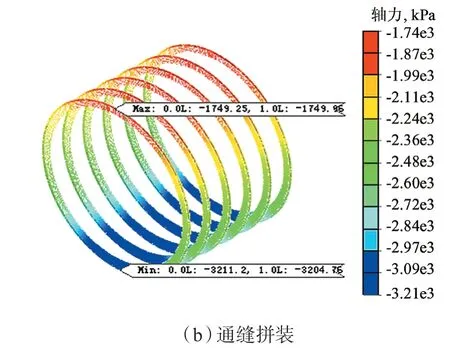
图13 不同管片拼装方式衬砌轴力图

图13 为通缝和错缝拼装方式下隧道衬砌轴力图。图中轴力以受拉为正，受压为负。可见，荷载作用下衬砌呈受压状态。错缝拼装时，随着衬砌环的旋转，每环的最大轴向应力位置也随之发生变化，衬砌最大轴向压应力为3.84×10kPa，位于环2 上。通缝拼装时，每一衬砌环的轴力分布基本一致，荷载作用下最大轴向应力为3.21×10kPa，位于环1 上。错缝拼装方式下的衬砌最大轴应力比通缝拼装方式下的大约19.6%。

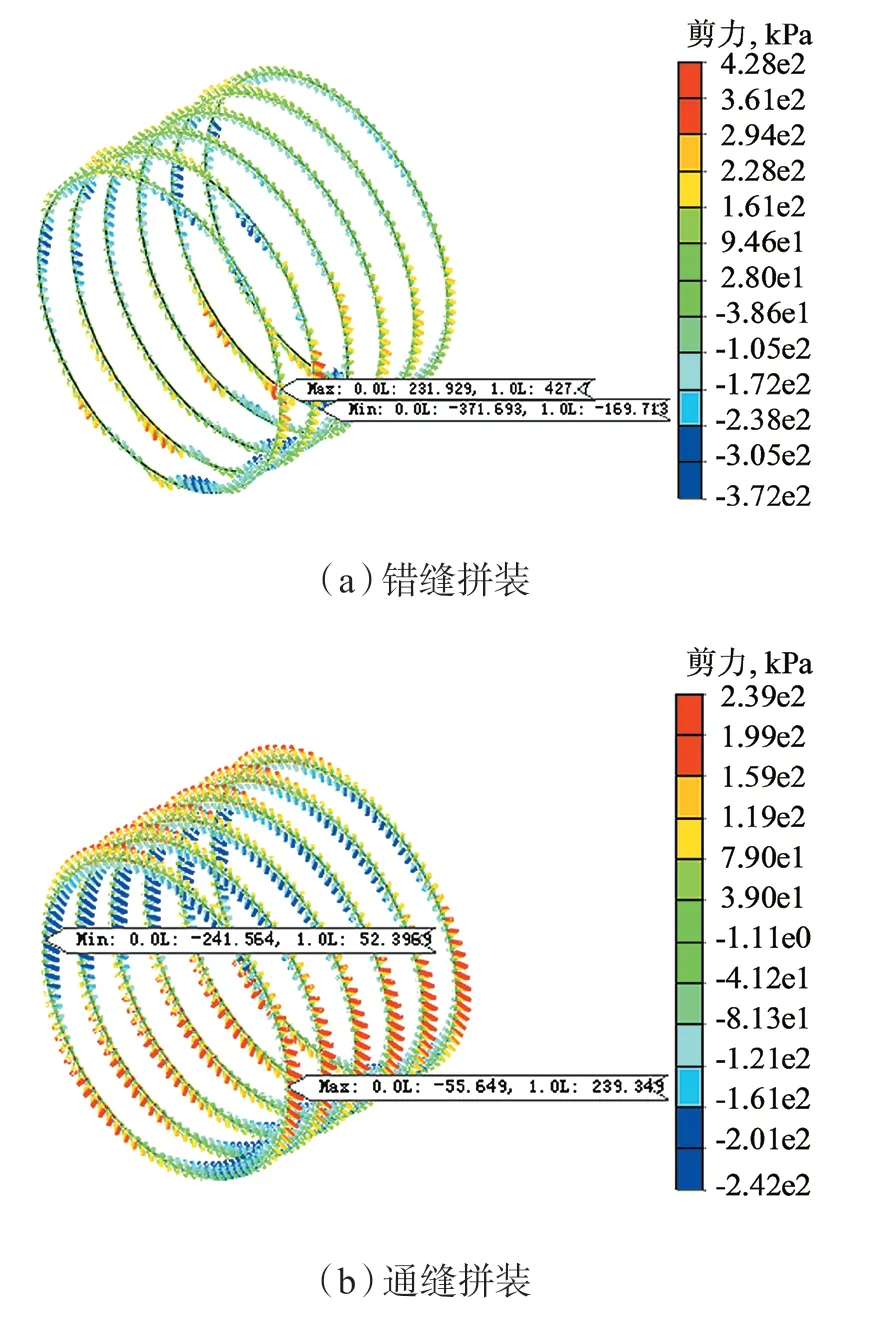
图14 不同管片拼装方式衬砌径向剪力图

图14 分别为错缝和通缝拼装方式下隧道衬砌剪力图。可见，错缝拼装时，随着衬砌环的旋转，每一衬砌环的剪应力分布均有所差异，最大剪应力为3.72×10kPa，发生在环5 上。通缝拼装时，每一衬砌环的剪应力分布基本一致，最大剪应力为2.42×10kPa，发生在环1 上。错缝拼装方式下的衬砌最大剪应力比通缝拼装方式下的大约54.0%。从数值上讲，错缝拼装和通风拼装条件下的剪应力均未超出衬砌材料的极限抗剪强度，不会对衬砌造成破坏。

3.3 弯矩分析

图15 为错缝和通缝拼装方式下隧道衬砌弯矩图。与前述一致，错缝拼装时，每一衬砌环的弯矩分布随着衬砌环的旋转发生变化，最大弯矩为5.34×10kN·m，发生在环5 上。通缝拼装时，每一衬砌环的弯矩分布基本一致，最大弯矩均位于隧道底部，最大弯矩值为2.26×10kN·m，发生在环1 上。错缝拼装方式下的衬砌最大弯矩约为通缝拼装方式下的2.36 倍。

图15 不同管片拼装方式衬砌弯矩图

4 结论与建议

本文以扬州瘦西湖盾构隧道为工程背景，建立隧道梁-弹簧计算模型，采用荷载结构法，分别对错缝和通缝两种拼装方式下隧道衬砌受力、变形特性进行了分析，得到如下结论：

（1）在相同地层、相同荷载条件下，错缝拼装与通缝拼装管片结构中的受拉、受压区域分布基本一致，但错缝拼装方式下衬砌位移、内力受衬砌环旋转角度影响，在隧道轴向上的分布没有通缝拼装下的均匀。

（2）错缝拼装较通缝拼装能减少隧道水平位移、竖向位移和角变形。就所研究的扬州瘦西湖隧道而言，在上述三方面，错缝拼装可较通缝拼装分别减少11.5%、27.7%和26.4%。

（3）错缝拼装方式下，管片轴力、剪力及弯矩最大值均大于通缝拼装方式下的相应值。就所研究的扬州瘦西湖隧道而言，在上述三方面，错缝拼装可较通缝拼装分别增大约19.6%、54.0%和2.36倍。

（4）错缝和通缝拼装相比，错缝拼装的管片更好地表现出了刚性衬砌的特点，变形小受力大；通缝拼装的管片更好地表现出了柔性衬砌的特点，变形大受力小。错缝拼装在变形、防水性能上优于通缝拼装，通缝拼装在受力、经济性能上优于错缝拼装。考虑到瘦西湖隧道工程投入大、境内水量丰富且对变形控制要求高，因此建议采用错缝拼装方式进行隧道施工。