钢框架在高温（火灾）下塑性力学特征分析

2021-06-07姜云鹏吴明涵孙强

安徽建筑大学学报 2021年1期

姜云鹏，吴明涵，孙强

（安徽建筑大学土木工程学院，安徽合肥 230601）

随着经济快速发展，在现代建筑新形势下，钢结构成为一种被广泛使用在高层和工业建筑中的建筑结构类型。钢结构除具有材质较均匀、塑性好、承载能力强、施工可靠性高等优势，钢材还是一种不易燃烧的材质，有较高的导热系数。在高温火灾条件下，钢结构自身会膨胀加快结构软化，钢材易由温度过高导致屈服强度降低而发生变形。同时钢框架节点处存在温差，导致不均匀受力，最终发生整体破坏。现阶段对房屋进行建筑设计时，往往忽视了结构的抗火能力，然而高层建筑火灾事件频发，使得钢结构建筑的抗火问题越来越引起重视。

目前，国内外对于钢框架在高温条件下的力学性能研究取得了一系列成果。强旭红等在不同火灾情况下对高强钢S460 进行材性试验，并与现有对国产钢Q460 和欧标钢S460 的研究成果进行比较，提出高强钢S460 在高温下的力学性能退化拟合公式。李国强等通过对高温下钢柱的极限承载力进行计算，并与有限元进行比较，分析出残余应力大小对和分布模式对极限承载力影响较小。夏月、余红霞等对约束是否影响火灾下刚节点强度展开深入研究。Dwaikat 教授研究得出在某一截面存在的温度梯度会导致截面内力发生变化的结论。蒋首超、李国强提出钢框架在局部高温下的温度内力简化计算的方法。虽然对于钢结构抗火方面的探究已有较大的进展，但是关于结构进入塑性阶段的研究较少。基于此，通过计算钢框架构件在高温下的温度弯矩和温度内力并结合力学知识，分析得出钢框架塑性铰出铰顺序，对两层两跨平面局部受火钢框架进行数值模拟分析并验证正确性，给平面钢框架结构建筑进行抗火设计提供一定的参考。

1 理论计算

1.1 基本假定

本文在对钢框架高温下进行塑性分析时，基于以下几个基本假定：

（1）变形均为小变形，对截面尺寸影响较小；

（2）所有载荷是线性递增的；

（3）荷载施加阶段，惯性力对结构的影响可忽略不计；

（4）塑性铰只发生在受力截面，对截面周围塑性区不产生影响；

（5）钢框架构件度有一定的刚性，达塑性极限状态时能够保持稳定。

1.2 工况实例

工况：两层两跨平面钢框架结构，柱间距6 m，层高4 m。柱端受水平集中P=10 kN，跨中受竖向集中力F=30 kN，两层两跨内部受火，梁、柱受火条件相同。梁、柱截面尺寸分别为M350×175×7×11和HM200×200×8×12（单位：mm），钢材选用Q235 钢材，梁为工字钢梁。受力简图如图1所示。

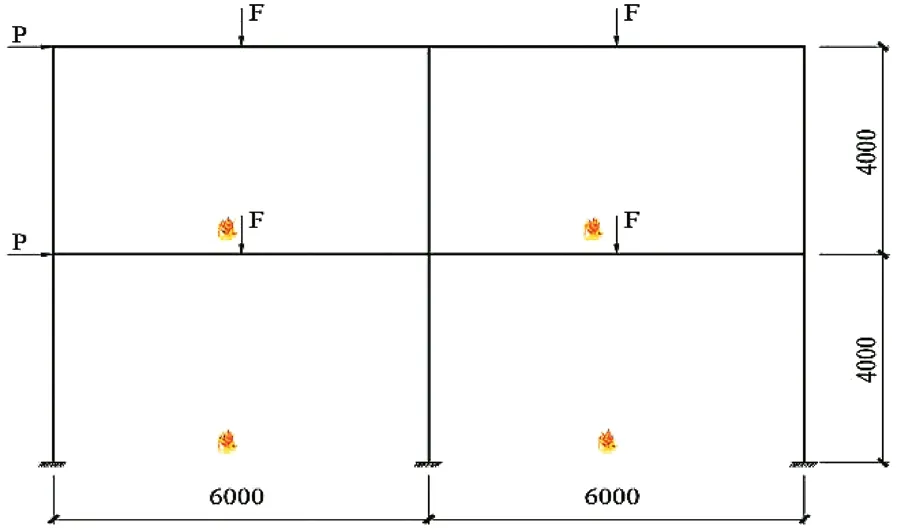
图1 钢框架受力简图

1.3 理论分析

引入高温下钢构件轴向温度内力N

高温下钢构件温度弯矩M（M）:

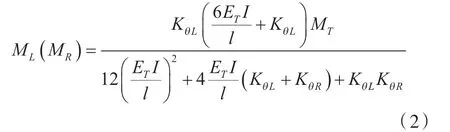
杆件转角θ：

式中:KT、K—柱轴向约束刚度；

K—约束转动刚度；

A—杆件截面面积；

l—计算长度；

T—杆件温度

T、T—杆件两侧温度；

θ—杆件转角；

E—温度（T+T）/2 时弹性模量；

α—材料热膨胀系数；

在梁柱初始温度T=20℃情况下，通过结构计算软件SPA2000 得到该工况在常温下的弯矩图，如图2 所示。

假定受火梁上下翼缘温度分别为300℃与400℃，梁温度分布不均匀。受火柱温度为200℃，柱温度分布均匀。为了方便计算，将钢框架结构内其他约束杆件近似看作施加在杆端的弹性约束。

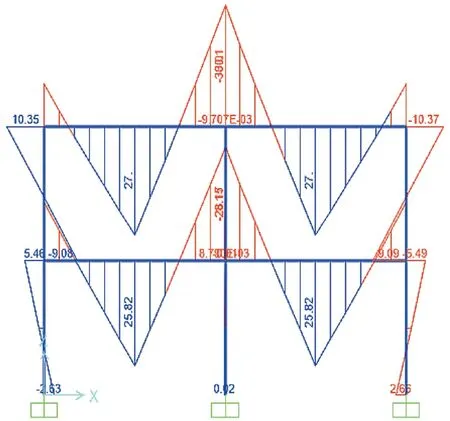
图2 工况在常温下的弯矩图

根据《局部火灾下钢框架温度内力的实用计算方法》中计算公式可算出K、K，代入（1）、（2）、（3）式可以计算出构件温度内力、温度弯矩，结果如表1 所示。

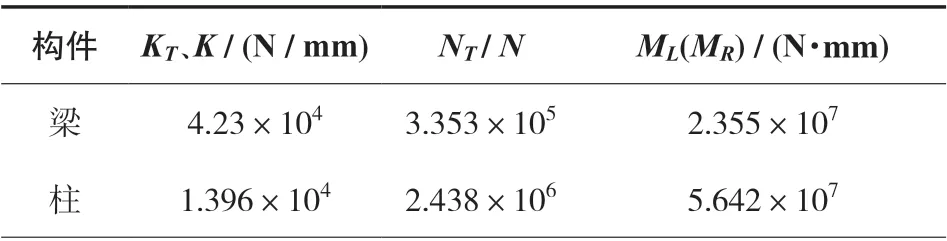
表1 构件温度内力和温度弯矩表

将表1 中求出的受火梁的温度内力和温度弯矩当做外荷载加到常温模型结点上，计算整个钢框架的内力变化情况。通过结构计算软件SPA2000得到该工况在高温下的弯矩图，如图3 所示：

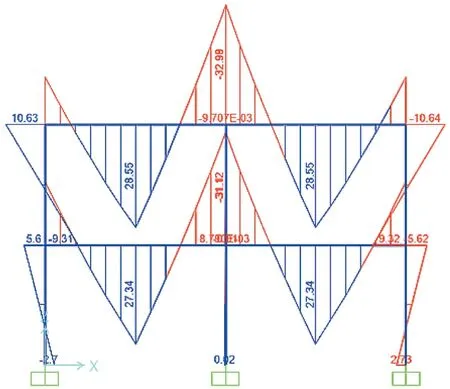
图3 工况在高温下弯矩图

从力学角度判断塑性铰出铰顺序：结合假定（4）、图4 可知，对构件施加外力，当截面弯矩达塑性极限弯矩M时，开始出现塑性铰，使截面发生转动，并传递小于等于M的弯矩。而在卸载后，截面能够传递反向弯矩，直到反向弯矩同样达塑性极限弯矩M，截面发生转动。对比图2、图3 可知：施加温度荷载后，构件弯矩逐渐增大。梁柱节点的弯矩最先达塑性极限弯矩，随后超过节点的极限弯矩，出现塑性铰。而后梁跨中节点和框架柱脚依次出铰。

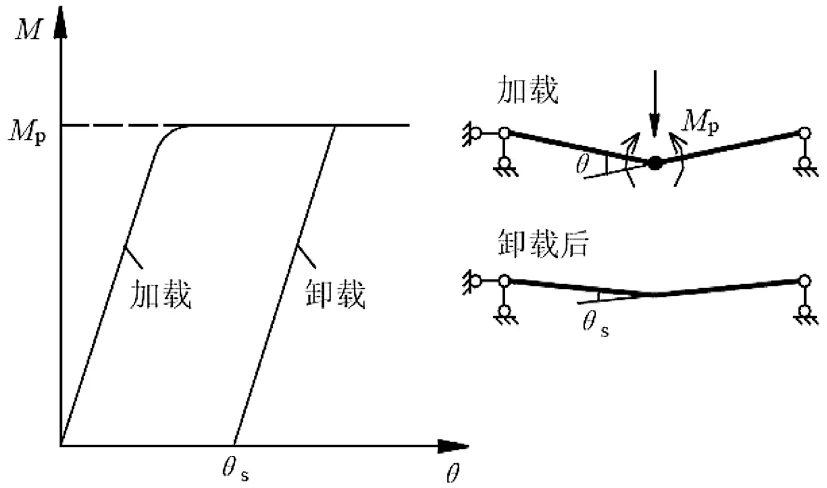
图4 塑性铰性质

2 数值分析

2.1 有限元模型的建立

本节利用ANSYS 数值模拟软件对工况进行模拟实验，模型尺寸同工况尺寸，模型建立如图5 所示。固定所有节点Z 方向位移（UZ），温度荷载以热传导形式在钢框架结构内传递，选用标准升温曲线ISO834 模拟结构环境温度与时间的关系。先采用SOLID70 八节点六面体单元进行温度场分析，再采用SOLID185 实体结构单元进行非线性有限元结构分析。将温度场受力与外荷载叠加求解。通过得到的节点应力大小和塑性应变发展顺序间接判断出塑性铰的出铰顺序。最终计算到1660 s（1660 s 是结构热力耦合作用破坏时刻）。在钢框架上选取关键点划分，关键点划分如图6 所示。

图5 有限元模型建立

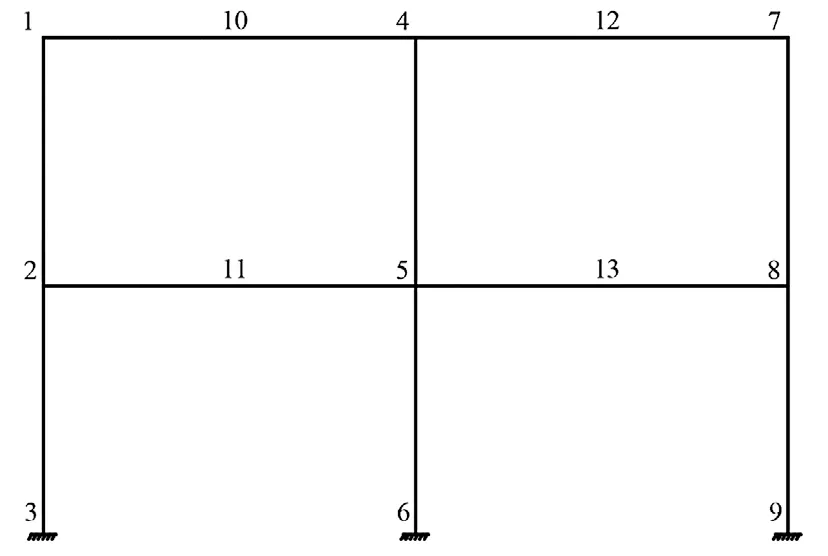
图6 两层一跨钢框架关键点划分示意图

2.2 热力耦合分析

对两层两跨钢框架进行热力耦合分析，将平面钢框架的应力分布情况以等效应力来探究。得出钢框架各关键点处应力平均值随时间变化情况，如表2 所示。

由表2 可知：升温初期，20～200 s 之间，关键点1、2 处应力的增幅最大，应力最大处在梁柱节点。这是由于温度不断升高，梁柱节点最大应力范围扩大，出现应力集中现象。200～400 s 之间，各关键点应力随温度升高不断增大，关键点1、2 处应力最大，最大应力位置由梁柱节点转向梁跨中，在高温条件下受力较大的区域更容易失去原有承载能力。由于钢梁逐渐失效，应力最大位置转向柱脚。400-1660 s 之间，随着温度不断升高，钢材的强度及钢框架节点的应力逐渐降低，整个钢框架的屈服应力逐渐减小。为方便分析，选取四个关键点并拟合应力随时间变化的曲线图，如图7 所示。

图7 节点应力随时间变化曲线

由图7 可知：选取的四个关键点的应力变化趋势大致相同。这是因为随着温度升高，节点应力不断增大。200℃后钢材自身应力和屈服强度均有所降低。当温度升高至某个温度时，该节点应力曲线同屈服强度下降曲线相交，说明该位置出现塑性铰。根据普通结构钢的高温屈服强度降低系数，得到钢材弹性阶段屈服强度随温度变化情况，作关键点4、5、6、11 各点应力与屈服强度的对比图，如图8 所示。框架受火梁、柱翼缘温度随时间变化曲线如图9 所示。结合图8、图9 可知：关键点4、5、11、6 处的应力曲线依次同屈服强度曲线相交，出铰时间依次为186 s、192 s、196 s、210 s。

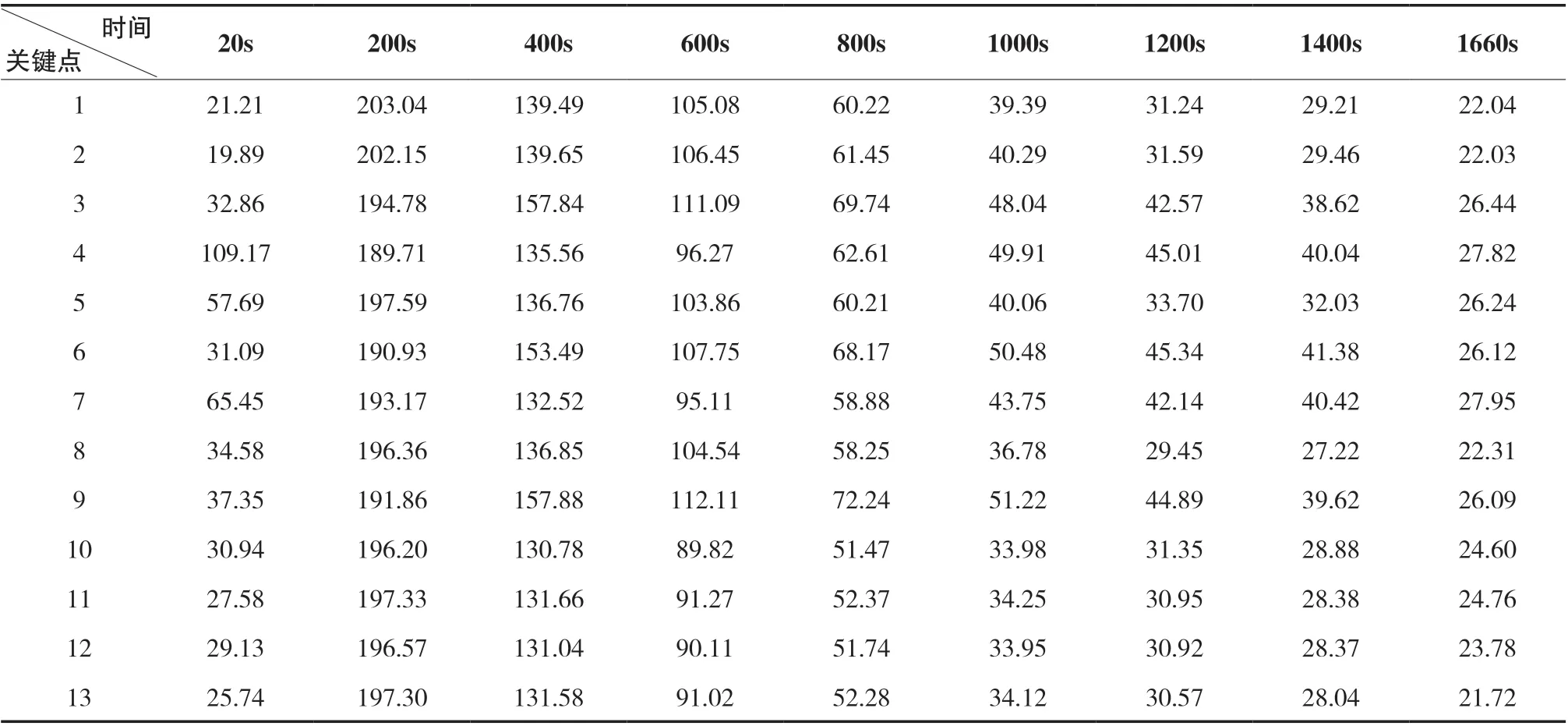
表2 钢框架各关键点处应力随时间变化表单位：MPa

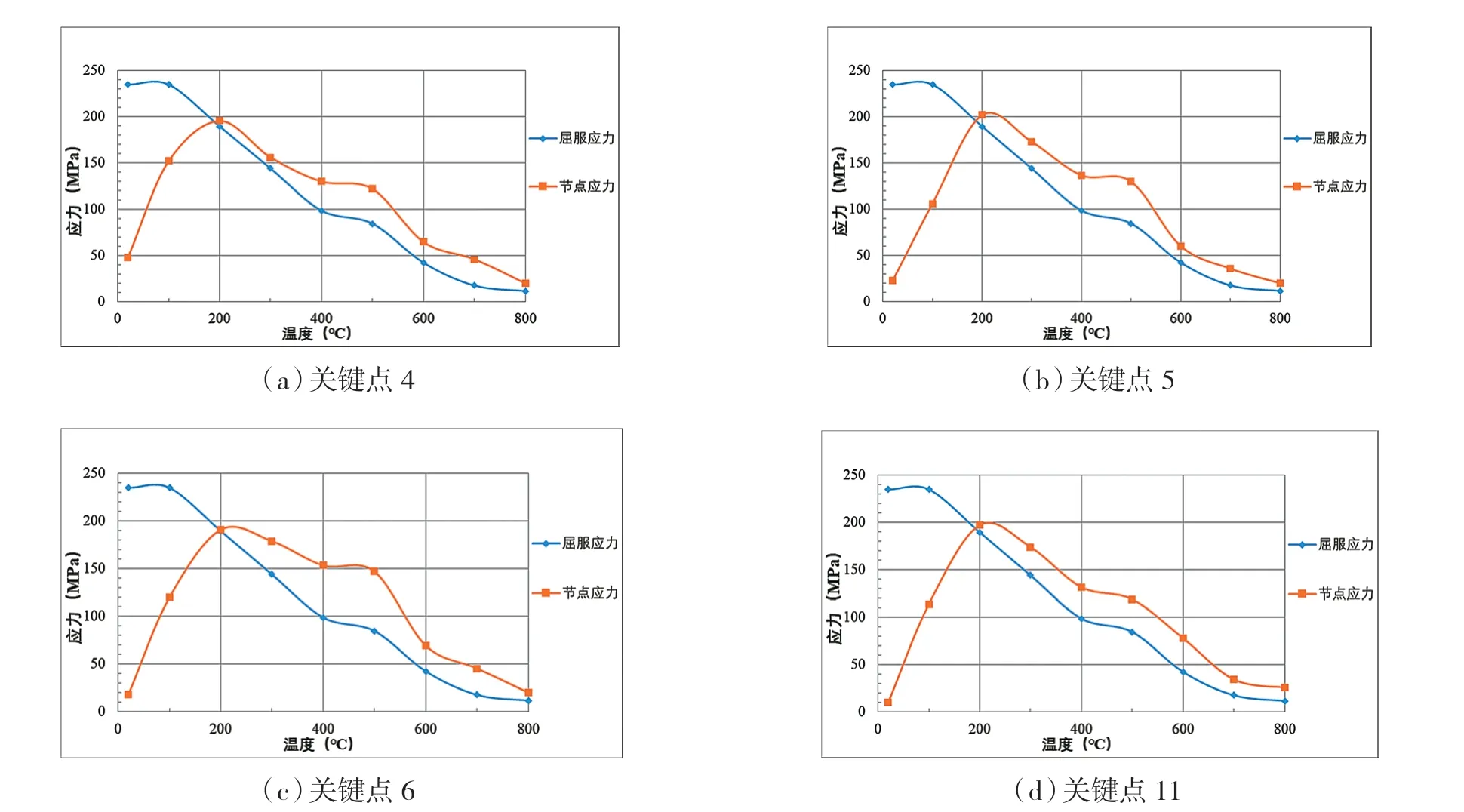
图8 关键点应力、屈服应力随温度变化曲线图

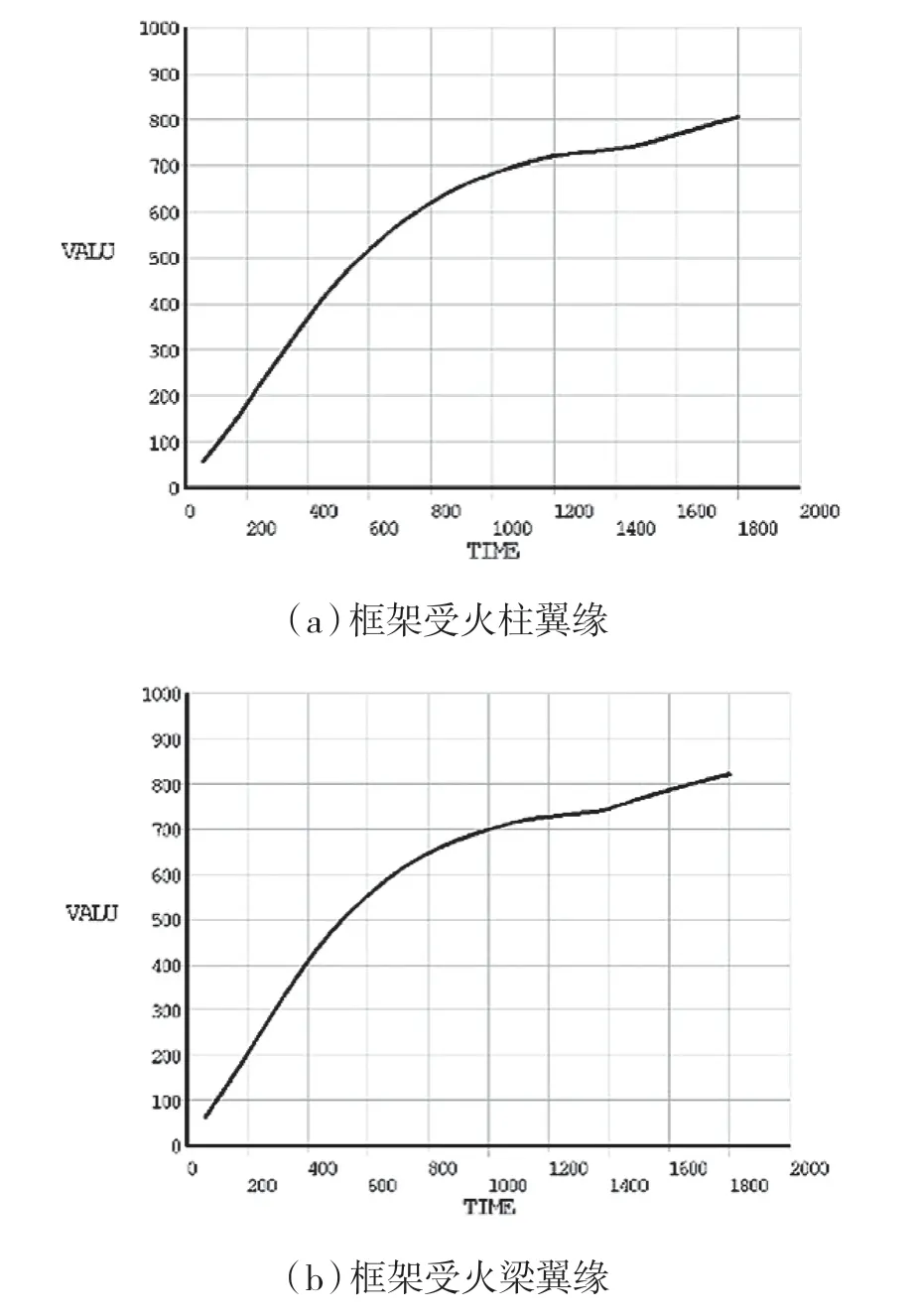
图9 受火梁、柱翼缘温度随时间变化曲线

由图10 可知：塑性应变最大处位置在中柱顶端。由于梁柱节点处和柱脚位置弯矩均较大，梁柱节点和柱脚位置的塑性应变随着温度升高而增大，梁柱连接处大面积进入塑性，而受火柱塑性应变相对较小，梁柱节点先于柱进入塑性阶段。随后在梁失效过程中，梁跨中位置塑性应变较大，出现塑性铰。随着温度继续升高，柱刚度逐渐降低，柱脚位置塑性铰形成。结合应力判断方法和塑性应变数据得出塑性铰出铰顺序依次为：受火梁柱节点先出铰，再到梁跨中位置，最后到柱脚位置。