实践探索，行而得知

程健

摘要：实践探索是数学课堂教学中常用的一种学习方式。 以五年级下册"解决问题的策略一一转化” 一课为例展开研究，发现实践探索对于数学思维的发展、数学思想的培养、数学方法的形成和数学知识的生成都有着重要的促进作用。

关键词：实践探索;数学思想;转化策略

陶行知先生曾说过：“行是知之始，认识来源于实 践，实践是认识的基础。”“实践探索”是近年来广受 师生喜爱的一种学习方式，这种方式融学生的观察、操 作、思考于一体，是一种具身的认知活动。孩子们通过 动手、动脑、动口等多方位的实践活动，参与数学知识 的探索过程，充分体验和感悟数学知识的形成，在此过 程中反复经历多次提出问题、解决问题的过程，对知识 的形成有了更全面的掌握。下面，笔者就执教的五年级 下册"解决问题的策略一转化” 一课，谈谈“实践探 索”在教学中的实施与感受。

一、实践探索促进数学思维的发展

匈牙利数学家波利亚说："数学既是一门系统性的 演绎科学，也是一种实验性的归纳科学。”毋庸置疑， 实践探索能让学生在做中学、学中思，“学思创共生”。 但是，实践探索不同于数学操作，数学操作是学生动手 能力的体现。在实际教学中，许多老师把实践探索和数 学操作混为一谈，将两者等同起来，学生在实践探索中 往往沦落为一个"操作工人”，只停留在动手操作中， 而失去了对问题的思考。实践探索不仅仅体现为学生的 动手能力，更为重要的是學生思维能力的体现，所以实践探索可以说是一种"具身认知”。

案例1：教学例1，突出转化优势。

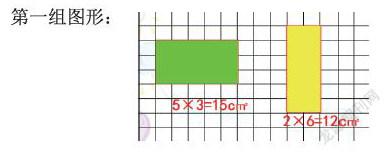
（1）比较两个图形的面积。（长方形）

第一组图形：

说说你是怎么比的？计算长方形的面积。

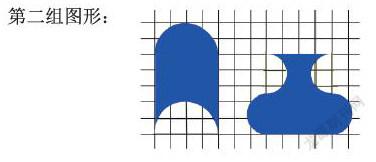
第二组图形：

师：你能通过直接计算比较出这两个图形的面积大 小吗？为什么？（图形不规则了）猜猜哪个面积大？

师：你们有没有好的办法来比较这两个图形的面积 大小呢？小组合作探究。

（2） 合作探究。要求：小组合作探究，每组拿出下 发的小组合作单及两个纸片模型，通过想一想、画一画、 剪_剪、拼一拼等方法比较两个图形的大小。学生动手， 教师巡视指导。

小组交流：说说你们组是怎么比较的。

预设：剪拼，学生演示剪拼的过程。

（3） 课件演示割补的过程，教师边演示边讲解。讲 解中突出平移和旋转。（板书：平移、旋转）

师：转化成长方形就能比较出面积大小了。仔细观 察一下，在转化过程中，两个图形的什么变了，什么没 变？（板书：形状变了，面积不变）

师：这就是转化方法中的一种常用方法一等积变 形。（板书：等积变形）

学生通过小组合作实践探究来比较两个不规则图形 的面积，通过动手剪一剪、拼一拼等实践活动，亲身经 历了问题的探究过程，明白可以运用平移、旋转等方法 实现转化。转化的策略在学生的直观操作中得到充分体 现，加深了学生对转化策略的体验。在这个实践探索活动中，学生不仅有了动手操作的亲身体验，同时伴随着 动手操作，学生的思维经历了从“如何求不规则图形面积“ 到"如何转化成规则图形"，再到"转化前后两个图形 面积怎样”等一系列发展过程，这才有了对转化策略的 深刻理解，也突出了实践探索对数学知识感性认识的重 要作用。

二、实践探索促进数学思想的培养

《义务教育数学课程标准》在"实施建议”中指出： 数学思想蕴含在数学知识形成、发展和应用的过程中， 是数学知识和方法在更高层次上的抽象与概括。在课堂 教学中，教师在传授数学知识的同时，更要渗透正确的 数学思想，培养学生解决生活实际问题的能力，让他们 以不变应万变，受益终身。王永春老师指出：“每一个 新知识都是在已有知识的基础上发展的，要善于运用类 比推理和比较差异的思想方法进行新旧知识的转化，达到 触类旁通、方法迁移的目的。"因此，“转化”就成了 一种重要的数学思想。

案例1：通过小组合作实践探究，探索比较两个不规则 图形的面积，学生每组拿出下发的小组合作单及两个纸 片模型，通过想一想、画一画、剪一剪、拼一拼等方法 比较两个图形的大小。各组学生都能想到把不规则图形 转化成规则图形，但是，如何转化是一个开放性过程， 尤其是第二个图形。在交流时，笔者发现学生用了不同 的转化方法。

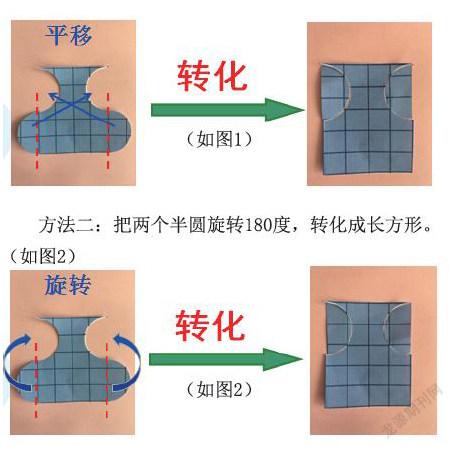
方法一：把两个半圆分别通过两次平移的方法，转 化成长方形。（如图1）

方法二：把两个半圆旋转180度，转化成长方形。（如图2）

方法三：把图形沿中间对称轴剪开，一半翻转后拼 成长方形。（如图3）

在合作实践探究过程中，学生发挥各自的想法，釆 用多种方法将不规则图形转化成了长方形。这样不仅让 学生学会了用不同的方法来实现转化，更帮助学生建立 和培养了 “转化”的数学思想。在这一系列的动手实践 活动中，学生充分感受知识实践性的生成过程，由知识 催生方法，再由方法上升为思想，培养学生的转化思想， 并能在解决实际问题中灵活运用。

三、实践探索促进数学方法的形成

案例2：回顾、反思、小结。

师：刚才，我们通过平移和旋转的方法把这两个复 杂的图形转化成简单的长方形，方便了我们比较。（板 书：复杂一简单）下面让我们来看看另外几个图形的面 积问题。（用分数表示各图中的涂色部分）

师：我们再来看几个图形的面积问题。请你说说你 是怎么想的？最后的图形如果摆正了，边长是多少？

师小结：上面这些不规则图形，我们同样可以通过平 移、旋转等方法把它们转化成怎样的图形？规则图形。 其实，就是把较复杂的问题转化成了较简单的问题。（板 书：不规则一规则）

学生通过实践探索，亲身经历了通过平移、旋转将 不规则图形转化为规则图形的过程，在充分思考图形转 化策略的同时，也对图形面积的转化方法有了一定的积 累，平移、旋转成了他们完成转化的有效方法。形成了 特定的方法后，在接下来用分数表示涂色部分的面积的练 习中，学生有了明确的方法，知道运用转化的策略解决 问题。对于最后一题，学生能发散出多种平移和旋转的 方藻实现面积转化，但是最后发现，无论哪一种撫， 其实都实现了把不规则转化成规则图形，使问题简单化 To由此，学生经历了从数学思想到数学方法、再由数 学方法回归到数学思想的解决过程。

案例3：图形周长。

师：图形的面积问题可以通过平移、旋转来转化，那 图形调整的周长问题可以转化吗？要求这个图形的周长， 它是一个什么样的图形？你能指出它的周长吗？周长好 求吗？

师：你有什么办法来求它的周长呢？

课件演示学生的想法：可以把竖直的线段怎么平移？ 横的线段呢？

师：在这个转化过程中，你又有什么变与不变的发 现呢？（板书：形状变了，周长不变）我们也给这个转 化起一个名字，叫“等长变形”。

师：周长计算中的转化（练习十六1）。

（1） 格子图中这个图形的周长，你会求吗？请你在 练习纸上画一画，并算出周长。

（2） 交流：说说你是怎么想的？（投影、课件演示） 延续着图形的面积问题，图形周长问题的研究同样

从学生的实践探索着手。在明确图形周长的概念后，学 生有了对图形周长的思考：“怎样使这些线段围成规则图 形呢？ ”在问题的驱动下，学生产生了方法的迁移，他 们能想到通过平移线段的方法来转化成规则图形的周长。 在学生亲身经历了这样的实践探索后，再让他们来看练 习十六的问题，学生更是明白了周长转化的正确方法， 能用语言将方法精准归纳为“竖直线段左右平移，横线 段上下平移”。当然，方法是为转化策略服务的，但对 具体方法的掌握也是运用转化策略解决问题能力的培养 和提高途径。

因此，在教学时，教师在教会学生各种方法的同时， 更要帮助他们跳出这些具体方法，树立转化的数学思想， 通过数学思想让他们的思维更宽广。

四、实践探索促进数学知识的生成

数学知识的学习是学生从具体逐步走向抽象的认知 发展过程，尤其是到了高年级，学生学习数学要釆用操 作、想象与推理相结合的方式来促进知识的生成。

案例4：回顾转化实例，感受转化的价值。

谈话：同学们，其实"转化”的策略并不神秘，我 们曾经在不知不觉中用到了许多。比如，在平行四边形 面积公式的推导中，我们把平行四边形转化成长方形。 再如，计算除数是小数的除法时，我们利用商不变规律 转化成除数是整数的除法。那么，在图形和计算领域， 你还能想到哪些用到了转化策略的内容呢？

（1） 小组回顾：小组合作进行整理，并寫在小组表 格里。教师引导学生先回顾图形领域中运用的转化策略， 再回顾计算及数与代数领域运用的转化策略。

（2） 学生小组交流后汇报，结合课件演示。

图形面积：平行四边形、三角形、梯形、圆形的面 积推导。

周长、内角和：化曲为直求树叶周长，把三角形三 个角转化成平角求内角和

计算：小数乘法转化为整数乘法、分数比较大小转 化成小数、简便计算。

（3） 小结：回顾和整理了这么多关于运用转化策略 的例子，你有没有发现这些运用转化策略解决问题的过 程有什么共同点？

在经历了图形面积转化和图形周长转化后，学生对 图形转化有了一定的理解，并逐步自主建立了转化的概 念：转化就是把复杂转化为简单，把不规则转化为规则。 接着，教师介绍平行四边形面积推导和除数是小数的除 法两个例子，使学生产生推理思想，形成对转化的进一 步理解，即转化就是由一种形态转化到另一种形态，充分 完善了转化策略的内涵。然后，学生根据这一发现来归 纳用转化策略解决过的数学问题，形成一种知识的归纳。 这样从具体图形问题抽象出数学策略，再由数学策略又 回归到具体学过的数学知识，充分体现了数学知识的生 成过程，也体现了学习数学的价值意义。

实践探索对于学生的思维发展，数学思想、方法的 形成，以及数学知识的生成，都有着十分重要的意义。 所以，在课堂教学中，教师要正确引导学生主动参与实 践探索，初步学会先思考后操作、边操作边思考的探索 方法，鼓励他们与别人分享和交流实践探索的过程和成 果，不断积累操作经验，提高在实践探索中学习数学的 能力。

参考文献：

[1]郑俊选.小学数学教学改革实践与研究W].北京： 人民教育出版社，2003.

（责任编辑：吴延甲）