机载俯仰多通道气象雷达地杂波抑制新算法*

（南京航空航天大学雷达成像与微波光子技术教育部重点实验室 南京 211106）

1 引言

机载气象雷达通过发射和接收电磁波探测航线或目标区域的气象情况，从而预警飞行员规避恶劣的气象状况（雷暴雨，湍流等），极大的保证了航路的安全。由于气象目标的性质和区域体分布的特点［1］，实际处理中主要通过估计气象回波的统计特性区分气象目标的类别和强度。当机载气象雷达处于下视状态时，回波中存在大量的地面散射回波（地杂波），干扰甚至淹没气象回波，导致高强度气象“虚警”概率提升，而抑制地杂波可能造成的气象目标能量损失又会导致气象目标误检，影响飞行员的判断。因此如何在抑制地杂波的同时，尽可能地保留气象信息，是气象雷达信号处理里面的一个关键问题。

气象雷达通常安装于飞机前端，天线前视扫描的工作方式以及载机的运动使得回波的多普勒谱展宽，从而造成杂波与气象频谱重叠等问题［2］，使得常规的频域滤波方法效果不理想。而在快时间域分离地杂波的方法，比如波束多扫描法［3］，基于地形数据库的地杂波抑制法［4］，其主要使用雷达在不同下俯角时得到的数据，计算分离处于不同距离门的气象和地，当气象和地处于等距离环上时，抑制效果不理想。但此时气象和地相对于雷达的下俯角不同，可以通过俯仰排列的天线阵列进行地杂波抑制［6］。文献［7］提出了一种基于空域滤波（相控阵）的气象雷达地杂波抑制方法，采用鲁棒的自适应零点波束形成算法抑制地基气象雷达回波中的地杂波，并通过实测数据验证了使用空域滤波方法进行地杂波抑制的可行性。

在上述空域滤波思想的基础上，根据机载雷达的数据接收空间几何关系，以及气象目标空间体分布的特点，本文采用垂直（俯仰维）排列的天线阵进行自适应波束形成，并提出了一种基于协方差矩阵重构的鲁棒波束形成算法进行地杂波抑制。通过仿真实验和仿真数据处理，证明了该方法收敛速度快，所需样本数少，并能够有效提高算法对协方差矩阵失配的鲁邦性，能够在保留气象信息的同时，抑制地杂波。

本文结构安排如下：首先建立了机载俯仰多通道接收系统气象雷达的回波信号模型；在此基础上，提出了基于协方差矩阵重构（CMR）的鲁棒波束形成算法；最后通过仿真实验和仿真数据处理，证明了算法的有效性。

2 机载俯仰多通道雷达回波信号模型

当雷达以一定的下俯角发射和接收脉冲时，回波在同一距离门上会同时存在气象回波和地杂波，如图1所示。由于地面散射点后向散射功率极强，在快时间域上，地杂波会淹没气象回波，使得通过时域进行杂波抑制的方法效果很不理想，无法保证抑制地杂波的同时保持气象回波不失真。

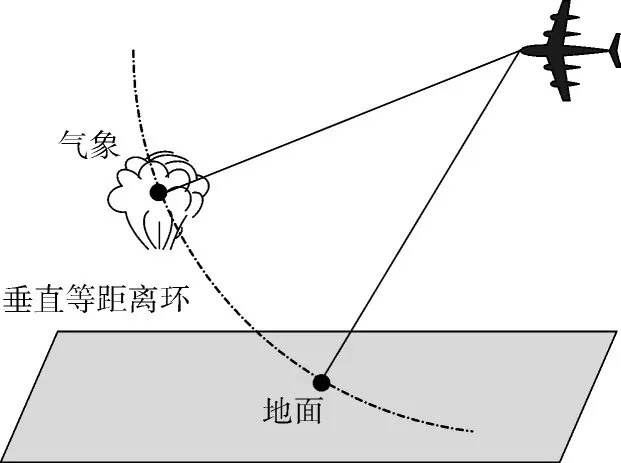
图1 气象雷达空间几何关系

从图1中可以看出，在俯仰维上，气象目标和地杂波与雷达之间的夹角存在较大差异，因此可以根据该空域信息，分离气象回波和地杂波，从而达到抑制地杂波的目的。我们可以采用垂直排列的阵列雷达（俯仰维相控阵雷达），通过空域自适应处理的方法，在保留气象信息的同时，抑制回波信号中的地杂波。

本文研究的地杂波仅考虑地面的回波，而气象目标为体目标，可将波束范围内的气象目标近似离散化为m个气象散射点，其接收数据示意图如图2所示，由于高度不同，在俯仰维上，气象目标和地杂波与雷达之间的夹角存在差异，因此可以根据该空域信息，分离气象回波和地杂波，从而达到抑制地杂波的目的。我们可以采用垂直排列的阵列雷达（俯仰维相控阵雷达），通过空域自适应处理的方法，在保留气象信息的同时，抑制回波信号中的地杂波。

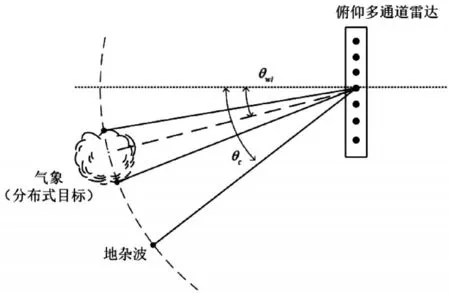
图2 多通道雷达接收数据示意图

不妨设相控阵天线为均匀线阵（ULA），其工作方式为一发多收模式，雷达波长为λ，通道数为N，阵元间隔为d。为防止空域混叠，阵列满足半波长间隔条件，即d=λ/2。在回波数据录取中，某一距离环内同时存在地杂波和气象目标散射点，俯仰角分别为θc和θwi，其中θwi指第i个气象目标散射点对应的下俯角（i≤m），上标T表示转置运算。雷达发射线性调频信号，接收回波并进行脉冲压缩后，该距离门接收信号的空域快拍（N×1维列向量）可表示为

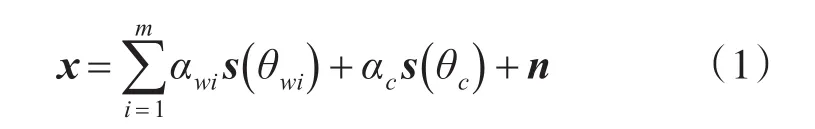
其中，n表示快拍中的接收机白噪声分量，与其他分量相互独立，αwi、αc分别表示第i个气象目标离散点回波和地杂波的复幅度，分别为第i个气象目标离散点回波和地杂波的理论空域导引矢量，可分别表示为

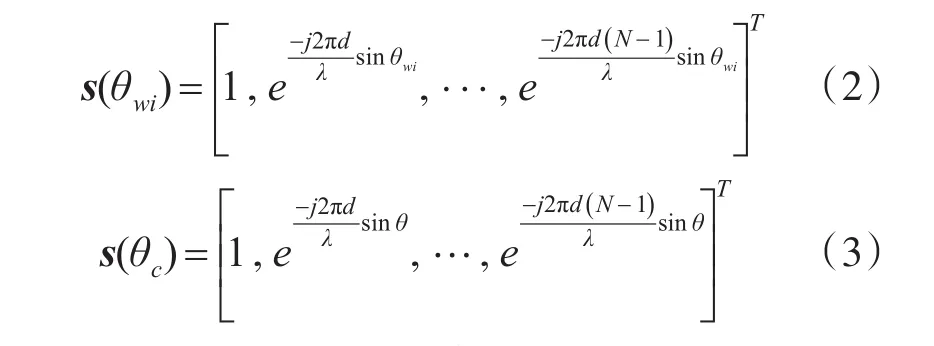
一般而言，可假设接收信号中的地杂波和气象分量统计独立并且期望为零，则接收信号x对应的协方差矩阵可表示为

其中，上标H表示共轭转置运算，E{}·为求数学期望运算，Rs和Rc+n分别表示期望信号的协方差矩阵和杂波与噪声的协方差矩阵。

假设阵列处理的权矢量为N×1维列向量w，，则输出信号可以表示为

俯仰维相控阵雷达的自适应信号处理流程可以由图3来表示。对每个通道进行自适应加权后，其输出功率可以表示为

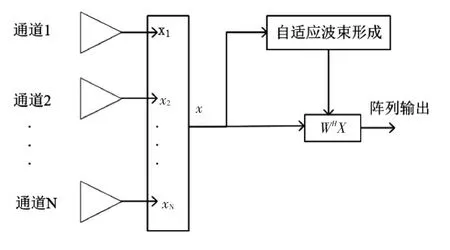
图3 信号处理流程

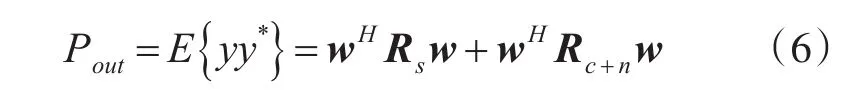
可以列出阵列输出信杂噪比如式（7）所示：

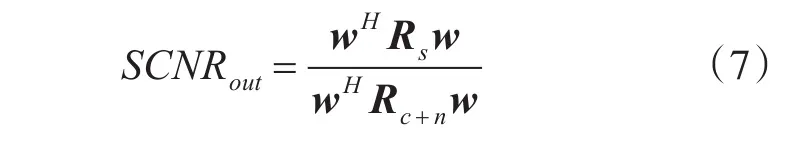
在高斯杂波及噪声的背景下，最优的阵列信号处理准则，即为最大化输出信杂噪比准则（MSCNR），能够在确定虚警率下最大化检测概率。传统的自适应波束形成算法如最小均方无畸变准则（MVDR）等，其假定目标来向角唯一，设为θ'。此时期望信号的输出功率可以表示为

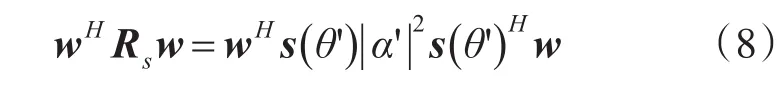
其中s(θ')是期望信号的空域导引矢量，α'是期望信号回波的复幅度。为了保证期望信号不失真 ，设θ'方 向 的 自 适 应 天 线 增 益 为 1，即。此时MSCNR可以表示为

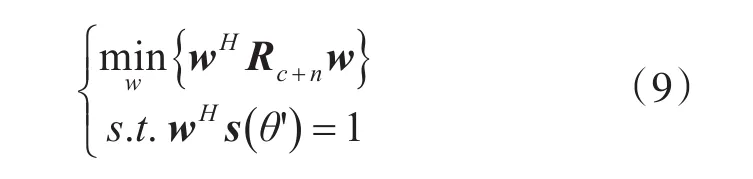
根据拉格朗日乘子法，可以解得，在期望信号来向角唯一时，最优权矢量为

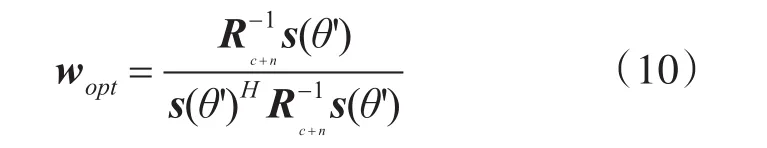
3 基于协方差矩阵重构的鲁棒波束形成算法

气象雷达探测的目标主要是群聚性弥散目标，在空间上呈无序性体分布［1］。从数学上表示，期望信号的协方差矩阵Rs的秩大于1，也就是说其期望信号来向角个数大于1个，无法用单个期望信号来向角约束计算最优权矢量。

为了提高气象信号的检测概率，需要尽可能的减少杂波和噪声功率，即最大化阵列输出信杂噪比；为了保证阵列输出的期望信号不失真，需设立约束使输出的期望信号功率等于常数，即wHRsw=t，由式（7）可知，权矢量的倍乘并不会改变输出信杂噪比的大小，因此不妨设t=1。综合上述条件，此时MSCNR可以表示为

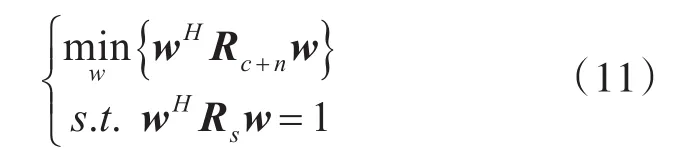
根据拉格朗日乘子法，设代价函数为

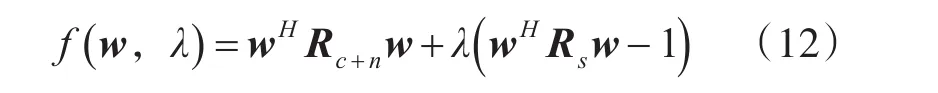
其中λ为拉格朗日乘子，将代价函数对加权向量求导等于零可以得到

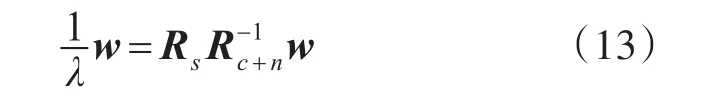
可以得出当λ最小时，阵列输出的信杂噪比最小。由式（14）可以推出，MSCNR准则下分布式目标的最优权矢量即为矩阵的最大特征值对应的特征向量，公式表示为

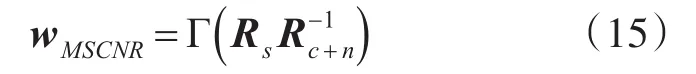
其中函数Γ（X）表示矩阵X最大特征值对应的特征向量。

在气象回波处理中，设雷达波束中心在俯仰向角度为ξ，为了减少气象信号的功率损失，不妨设ξ角度对应的自适应天线增益为1，即wHs()ξ=1，在该约束条件下可以得到最优权矢量为

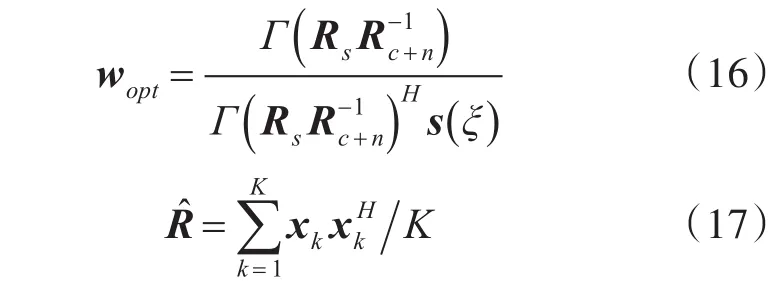
由式（14）可知，Rc+n可以用R等效替代。在实际处理中一般用样本协方差矩阵来估计R［8］，如式（17）所示，其中，K为信号样本数，Rs一般直接用理论期望信号协方差矩阵来替代，样本矩阵求逆（SMI）算法［9］。但无论是理论期望信号协方差矩阵或是样本估计的信号协方差矩阵都与真实的协方差矩阵之间存在一定的差距，即协方差矩阵失配问题。而SMI算法对该问题具有弱鲁棒性［11］，并且SMI算法的收敛速度低，难以满足实际处理的需求。

为了提高算法对协方差矩阵失配的鲁棒性，并提高算法的收敛速度，本文基于协方差矩阵重构（CMR）的MSCNR方法［12］，重构信号协方差矩阵以及杂波和噪声协方差矩阵，从而进行鲁棒波束形成。其重构方法可以表示为

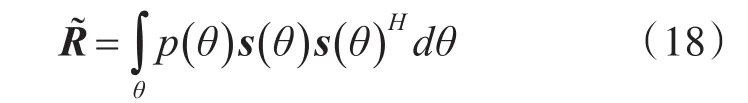
其中s(θ)为对应θ角的空域导引矢量，p(θ)为回波的空域功率谱密度，通过回波MVDR谱估计得到，即

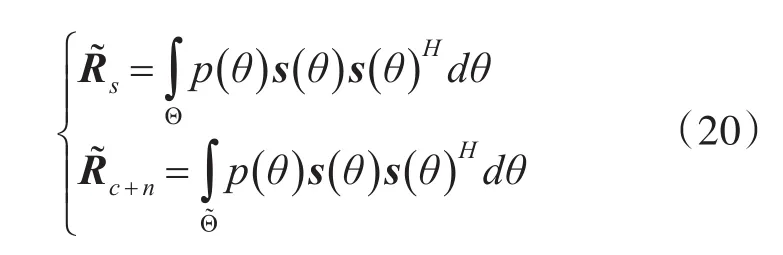
代入式（16）可以得到基于协方差矩阵重构的分布式气象目标波束形成最优权矢量：

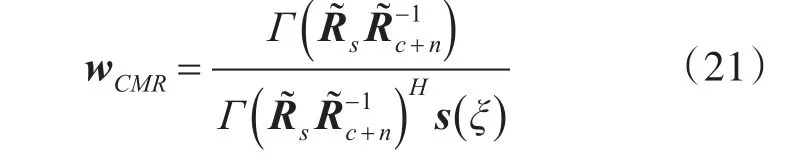
4 仿真实验结果与分析

假设接收阵列为均匀线阵（ULA），其实验参数设置如表1所示，计算本文提出的CMR算法的收敛速度，其对比算法是SMI，对角加载的样本矩阵求逆法（LSMI）以及最坏情况下最优算法（WPO），结果如图4所示。其中LSMI中的加载因子为噪声功率5dB，做30次Monte Carlo试验，做平均后得到收敛速度曲线如图4所示。可以明显看出基于CMR算法的收敛速度远大于SMI和LSMI以及最坏情况下最优算法，并且在小样本下，CMR算法能够实现较小的信杂噪比损耗，能很好地满足实际处理时的需求。

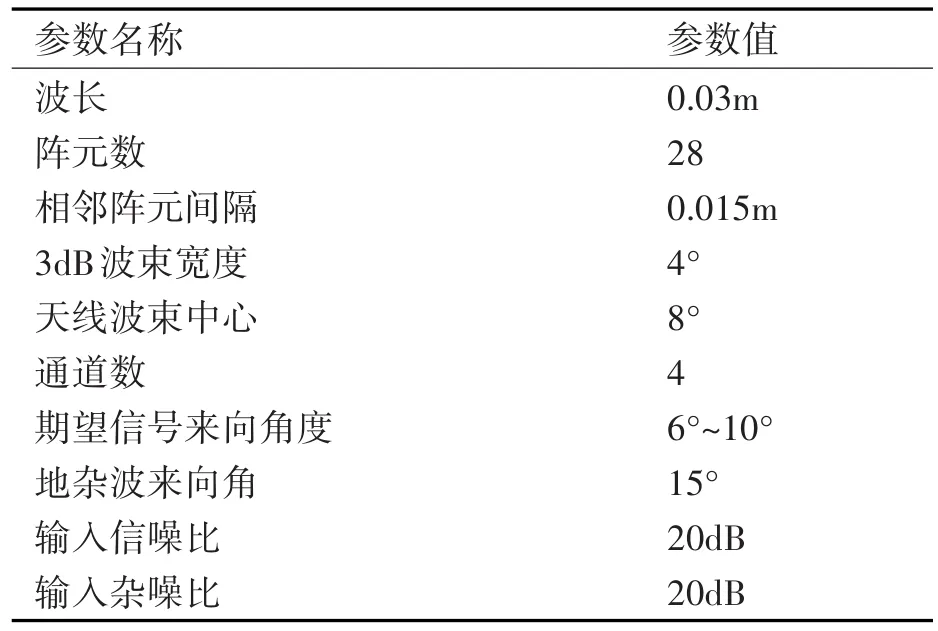
表1 CMR算法性能验证实验参数列表

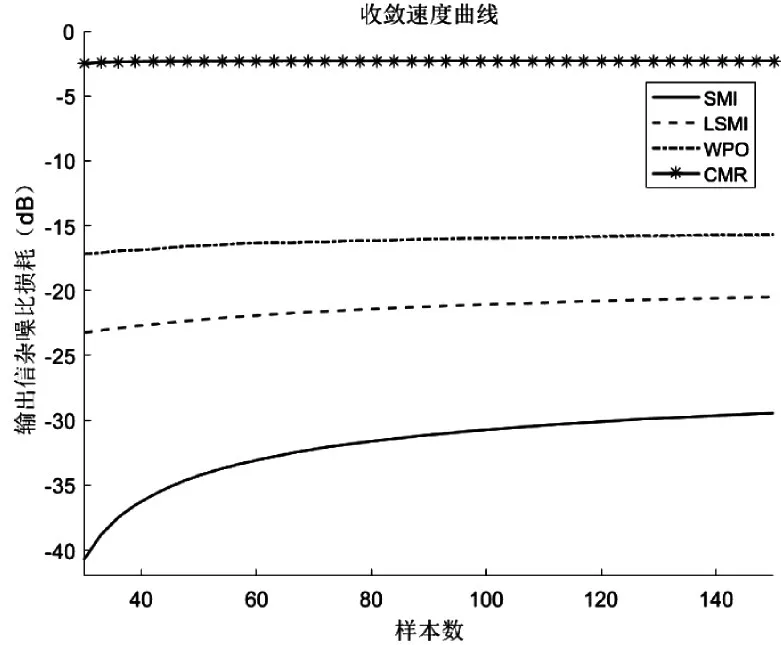
图4 收敛速度曲线

为了进一步证明本文提出的算法在分布式期望信号条件下的算法性能，本文重点采用自适应方向图（AP）和信杂噪比改善因子（SCNR-IF）对算法的性能进行分析，其中改善因子定义为输出端（自适应处理后）SCNR与输入端（自适应处理前）SCNR的比值。

其余实验条件不变，计算CMR算法得到的AP如图5所示，自适应天线方向图在杂波所在位置形成了较深的凹口，证明了其具备对杂波的抑制能力。此外，AP在目标所在位置形成了主波束，从而保证了气象目标能够无失真地通过波束形成器。

图5 自适应天线方向图

其余条件不变，计算CMR算法杂波入射角度在（-10°，90°）范围内的SCNR-IF如图 6所示，可以看出除气象目标所在方向（主瓣内）外，该算法均能够获得较高的SCNR改善，证明了算法具备较好的杂波抑制性能；同时在气象目标所在方向内，其曲线凹口平缓，能够减少主瓣内分布式期望信号的损失。

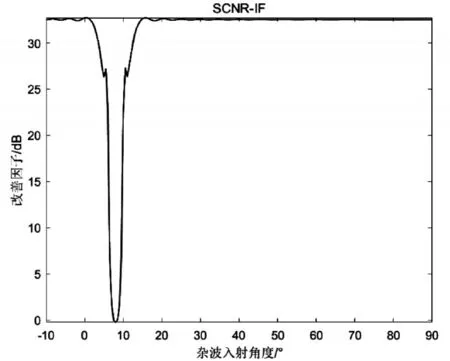
图6 改善因子

为了进一步验证本文提出方法的有效性，进行俯仰四通道气象仿真回波数据处理。其仿真条件设置如表2所示，雷达系统采取一发多收体制，在考虑地球曲率条件下，产生一组回波，并经过脉压后，气象目标回波数据如图7所示，含有气象、地杂波和噪声的数据如图8所示，其中红色矩形的位置处的气象回波被处于等距离环上的地杂波所淹没。对图8对应数据采用CMR算法进行杂波抑制处理，得到杂波抑制后的数据，如图9所示，其中样本协方差矩阵估计的样本点数为8个，两倍于通道数。

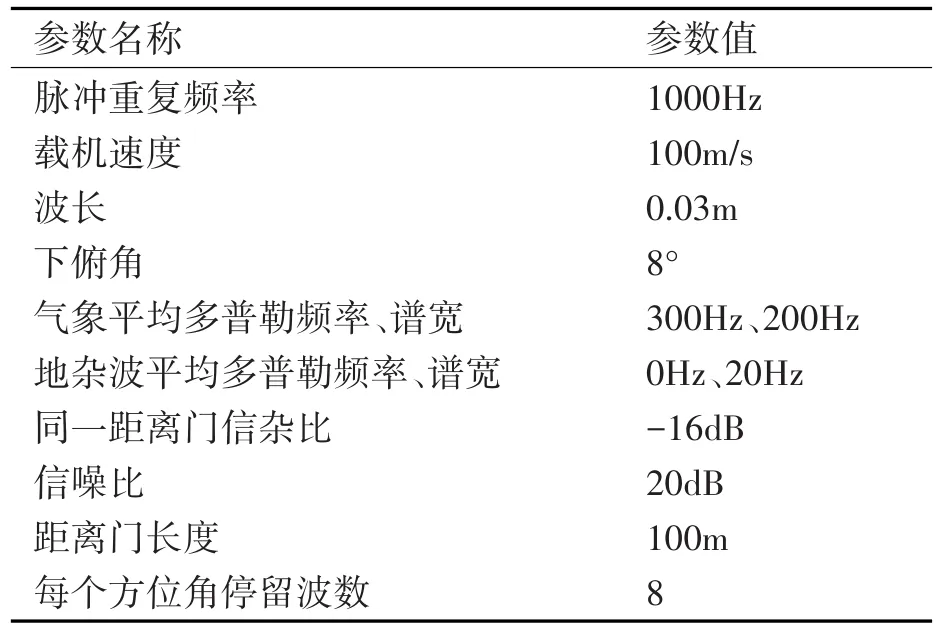
表2 机载四通道气象回波仿真参数列表

图7 气象目标回波信号

图8 仿真气象回波（含噪声与地杂波）

从图9中可以看出，杂波抑制后，气象回波等距离门上的地杂波以及噪声被基本抑制，可以直接从阵列输出中在快时间域（距离向）上提取出主瓣气象回波。而距雷达更远（近地）的地杂波因为在雷达主瓣内，无法使用波束形成算法进行抑制，残留在阵列输出的数据中。

图9 CMR算法杂波抑制输出结果

在图8中，选取第566，567，568距离门，-11.9°水平方位角位置的空域快拍信号，计算其MVDR谱，并用CMR算法计算自适应天线方向图，其结果如图10与图11所示。可以看出MVDR谱存在两个峰，一个峰位于主瓣内，是气象信号，因为气象是分布式目标，其MVDR谱较宽，对应角度的自适应天线增益趋于1，能够保留气象信号；另一个峰位于旁瓣内，是地杂波，对应角度自适应天线方向图存在深的凹口，能够抑制地杂波。

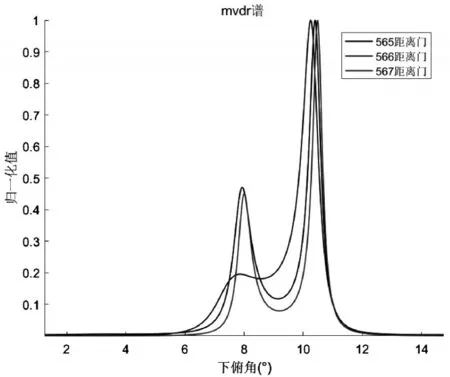
图10 MVDR谱

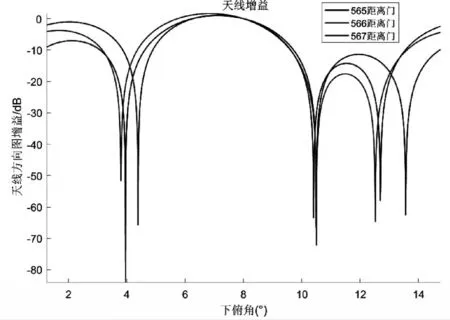
图11 自适应天线方向图

从回波强度上进行分析，取图8与图9对应数据距离门为［564，575］的区域（气象所在距离门），进行距离门平均后，画出其剖面图，如图12所示，从剖面图上可以看出，与气象处于同一距离门的地杂波得到基本抑制，气象回波得到保留，验证了CMR算法的有效性。

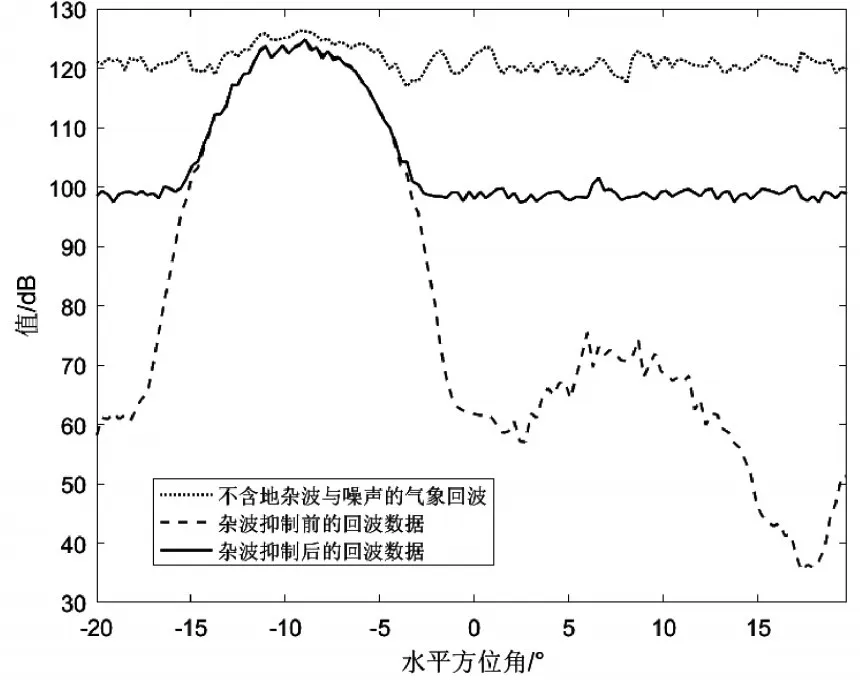
图12 564-575距离门平均后剖面图

从回波多普勒谱上进行分析，取图8，图9，图10对应数据第568距离门，水平扫描角度-11.9°的空域快拍信号进行频谱计算。进行多普勒补偿，抵消载机对地的速度影响后，得到多普勒频谱图，其结果如图13所示。从多普勒谱分析可以得出，回波中地杂波的成分（零频附近）被基本抑制，并且杂波抑制后的气象频谱主瓣损失小，形状与气象目标回波基本一致。

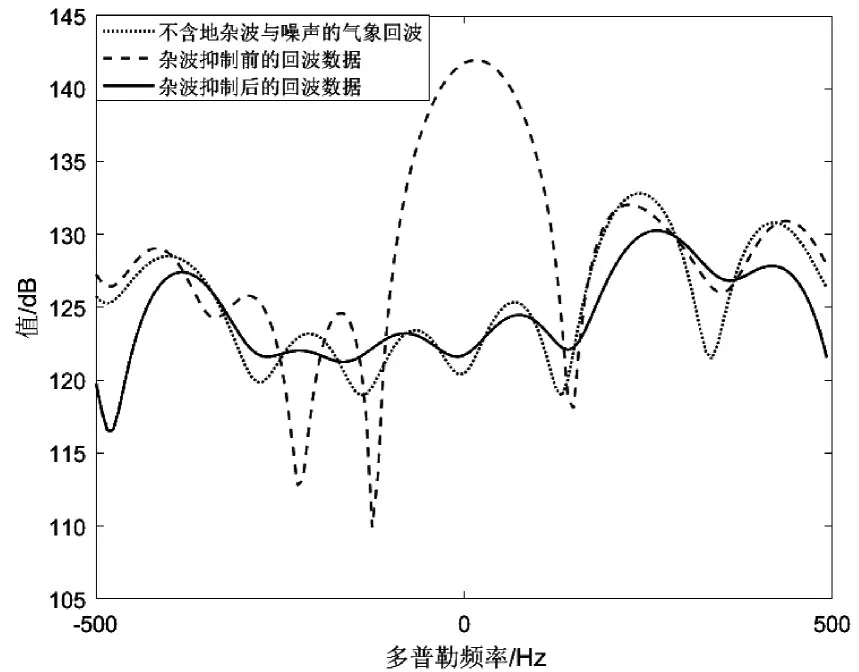
图13 多普勒频谱

通过仿真数据处理，证明了本文提出的基于协方差矩阵重构的鲁棒波束形成算法对协方差矩阵失配问题有较高的鲁棒性，可以有效保留机载气象雷达回波中的气象信息，并且抑制地杂波，证明了CMR算法对机载俯仰多通道气象雷达杂波抑制的有效性和可行性。

5 结语

机载气象雷达处于下视状态时，回波在同一距离门上会出现地杂波污染气象的情况。针对这个问题，本文首先证明了使用俯仰排列的均匀线阵（ULA）抑制地杂波的可行性，然后针对传统自适应波束形成算法收敛速度慢，对协方差矩阵失配弱鲁棒的问题，提出了基于协方差矩阵重构的MSCNR算法，通过计算信号的MVDR谱重构出目标协方差矩阵，最后计算得到加权矢量。通过仿真实验和仿真数据处理证明，该方法收敛速度快，计算所需样本数少，能够在保留气象信息的同时，有效抑制地杂波。