迁移 探究 思辨——《认识平行四边形》教学实践

文|戚洪祥

【教学内容】

苏教版四年级下册第88、89页。

【教学过程】

一、在旧知迁移中，理解平行四边形的概念

师：（PPT出示长方形）同学们，这是一个长方形，谁来说说你认识的长方形？

（学生说，教师板书：四个角、直角、相等、四条边、对边相等、对边平行）

师：（PPT出示另一个长方形）这个长方形有这些特征吗？生：有。

师：虽然大小不同，但只要是长方形都会有这些特征。

师：下面我用这两个长方形玩个小魔术。请大家看。（PPT出示下图）

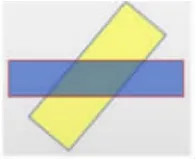
师：你看到了什么？请同学们拿出两种不同颜色的透明长方形薄片，像这样重叠。

（学生动手操作）

生：看到了一个四边形。

师：对于这个四边形，你能确定什么？（PPT凸显中间的四边形）

生：有四个角。

生：有四条边。

生：对边相等。

生：（质疑）不能确定“对边相等”，只能确定“对边平行”。

师：说说为什么？

生：因为原来的两个长方形对边是平行的，这里的对边是原来长方形对边的一部分，所以也应该是平行的。但“对边相等”此时是得不到的。

师：还有什么能确定的吗？通过观察，我们能发现这个图形有“四个角”“四条边”，这是每个四边形都有的特征。（板书：四边形）这位同学还发现了这个四边形的“对边平行”，我们把两组对边分别平行的四边形叫做平行四边形。（板书：平行）二年级时，我们已经初步认识了它，今天我们一起深入了解平行四边形。（板书课题）

【设计意图：学生在二年级时已经初步认识了平行四边形，对平行四边形已经有了直观的了解。通过复习长方形的特征，实现边、角探究图形特征的视角迁移。同时通过两个长方形的重叠引入新课，将长方形特征中的“对边平行”直接迁移至平行四边形，又直指定义中“对边平行”这一本质，实现数学语言的精准表达。】

二、在合作探究中，明晰平行四边形的特征

师：平行四边形还有什么特征呢？请大家拿出1号信封里的平行四边形，同桌两人一起来探究一下吧。（PPT出示探究要求）

探究要求：

1.想一想，平行四边形的边、角有什么特点？

2.做一做，选择合适的方法验证你的想法。

3.说一说，把你的结论和同桌分享。

（同桌合作学习，教师巡视并参与交流）

师：谁来汇报一下你们的发现？

生：我们通过测量发现了平行四边形的对边是相等的。这个平行四边形有两条边长10厘米，另外两条边都是6厘米。

师：还有没有研究对边长度的同学，你们的发现呢？

生：我们这个平行四边形的一组对边长12厘米，另一组对边长8厘米。

生：我们没有测量，而是把它对折后又对折了一下，这样也能看出相对的两条边是一样长的。

师：请同学们把目光聚集到这里，看这位同学的演示。

学生先上下对折，再左右对折。如下图所示）

师：好方法。除了对边相等，有没有其他发现？

生：我们发现了平行四边形的四个角中，有两个角是锐角，有两个角是钝角。

师：以你的平行四边形为例，指给同学们看一看。

（学生动手指并介绍，其余学生观察）

师：每个人手里的平行四边形是不是都有两个锐角和两个钝角？

生：是。

（教师修改板书“直角”为“两个锐角、两个钝角”）

师：还有其他发现吗？

生：我们发现这两个锐角和两个钝角是相对的，不在一起。

师：指给大家看一看。（学生指）他们发现两个锐角是相对的，两个钝角也是相对的，都不靠在一起。

生：我们用量角器量了平行四边形的四个角，发现两个锐角是相等的，两个钝角也相等。

师：大家动手量一量，看你们手里的平行四边形是不是这样的。

（学生动手测量，验证“对角相等”）

师：通过测量，我们发现了平行四边形“对角相等”。（修改板书“相等”为“对角相等”）

生：可以不用测量，我们是用研究三角形内角和的方法，把角撕下来比的。

师：比的结果怎样？

生：对角相等。

师：还有发现吗？

生：我们发现四个角中，锐角加钝角等于180°。

师：其余同学想一想，有没有办法验证他们的结论？选择一种方法验证一下。

（学生动手测量或撕角拼角验证，并汇报）

生：他们的结论是正确的。（板书：锐角+钝角=180°）

师：同学们，刚刚我们通过量一量、折一折、撕一撕、比一比、拼一拼的方法，发现了边、角的大小关系、位置关系，认识了平行四边形。

【设计意图：苏霍姆林斯基说过“儿童的智慧在他的手指尖上”，这句话道出了动手操作在学习中的作用。从“边”“角”两个维度探索平行四边形的特征，学生通过量长度、量角度、对折、撕角比角、撕角拼角等实践活动，发现了平行四边形边的长短关系、角的大小关系，还发现了“锐角和钝角的和为180°”这样的互补关系，超出了教师的课堂预设，这样精彩的动态生成源自于教师的放手、学生的实践。】

三、在直观想象中，把握平行四边形高的实质

师：咱们继续回到原来的两张长方形，如果这样不断地转动，可以得到许多个平行四边形。（PPT动画演示，并出示以下四幅图）

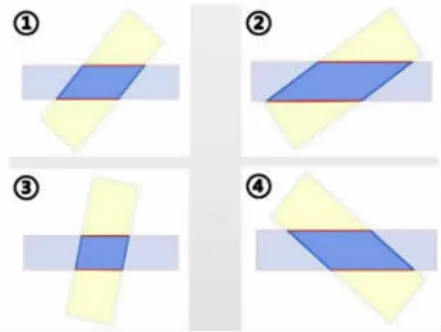
师：请同学们观察图中的四个平行四边形，想一想这四个图形之间有什么相同点和不同点呢？

师：老师给大家都准备了这四个平行四边形，请拿出2号信封，同桌一起研究，看看这四个平行四边形的相同点和不同点有哪些。

生：边不一样长。

生：角不一样大。

师：有什么相同点呢？

生：（动作演示）它们放到一起，上边与上边对齐，下边与下边对齐。

师：谁能听明白？能不能用数学语言把这句话重新表达一下？

生：就是上边到下边的距离是一样的。

师：请大家看着大屏幕上的四幅图，想一想，上边到下边的距离为什么会一样呢？

生：都等于那个不动的长方形的宽。

师：平行四边形对边的距离相等，都等于对应长方形的宽。（PPT动画演示，如下图）

师：除了上下对边的距离，换个角度，你还能看到什么？

生：斜着的两条边距离与旋转的长方形宽相等。

师：是的，这组对边的距离等于这个长方形的宽。（PPT动画演示）

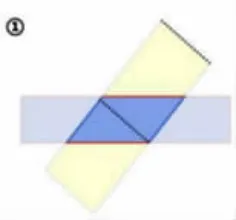
小结：从平行四边形一条边上的一点到它对边的垂直线段，是平行四边形的高，这条对边是平行四边形的底。（PPT动画出示）

师：请拿出刚刚的四个平行四边形，画出它的一条高，把它的底和高指给你的同桌看。

（学生动手画高并和同桌交流）

【设计意图：虽然有“三角形高”的认知基础，但图形的高因其“不可见”一直是教学的难点。为了突破这一难点，借助四个平行四边形的异同思辨，联系原来的两个长方形，从发现“平行线间的距离等于长方形的宽”这一结论切入，突破平行四边形高的教学难点。同时，依托长方形来学习平行四边形的高，为平行四边形的面积计算打下基础，做好铺垫。】

四、在深度思辨中，感受平行四边形的应用

师：老师这里有一个用四根小木条钉成的长方形，请仔细观察。（实物操作后，PPT出示下图）

师：你看到了什么？

生：我看到了长方形被拉成了平行四边形。

师：在拉的过程中，什么东西没变，什么东西变了？

生：平行四边形边的长度没有变，都与原来木条的长度相同。

生：这三个平行四边形的高在不断地变小。

师：是的，从左向右看三个图，高在不断变小。如果从右向左看呢？

生：高在不断地增加。

师：最多加到什么程度？

生：最多到长方形的宽。

师：刚才这些平行四边形都是由长方形木框推拉得到的。如果老师一开始就想用这四根木条钉成一个平行四边形，想象一下钉成的平行四边形是什么样子的？

（PPT出示一组平行四边形）

师：用四根木条拼成平行四边形，能拼出不同形状的平行四边形，这说明平行四边形具有易变形的特性。

师：平行四边形具有易变形的特性，使它在生活中有着广泛的应用。（PPT出示图片）校园伸缩门、伸缩楼梯中的平行四边形不断改变形状，自如地开与合、升与降，让我们的生活更加便捷。

【设计意图：苏教版教材在二年级时，已经预设了将长方形木框拉成平行四边形的学习活动，其形成的“拉得动”“不稳定”这些表象，并不是平行四边形易变形的数学本质。在推拉、观察之后，通过拼摆的方式，让学生准确感悟“平行四边形具有易变形特性”的数学道理。同时，将“易变形”这一数学属性与生活中的平行四边形进行联系，让学生感受到数学知识的应用价值。】