基于神经网络的航空发动机进口总压畸变重构研究

2021-06-02

燃气涡轮试验与研究 2021年1期

(中国飞行试验研究院，西安 710089)

1 引言

随着航空技术的不断发展，现代战斗机的飞行速度和机动性不断提高，航空发动机遭遇的进气总压畸变也更加严重[1-2]，传统采用预留足够稳定裕度的发动机稳定性设计方法所造成的发动机性能损失将变得不可接受。为解决发动机性能和稳定裕度的矛盾，畸变容限控制技术得到了发展和应用[3]。畸变容限控制技术将发动机进口畸变特征参数加入到发动机控制系统中，根据进气畸变水平动态调节发动机的稳定工作裕度，在畸变小时减小稳定裕度以提高发动机性能，在畸变较大时扩大稳定裕度以确保发动机稳定工作[4]。NASA 在1983 年至1987年和1993年至1998年分别开展了HIDEC(高度集成度数字电子控制)项目[5-6]和HISTEC(高稳定性发动机控制)项目[7-8]，目的就是演示验证发动机稳定性增强技术。

发动机畸变容限控制技术实现的一个重要基础，是在飞行中实时估算发动机进口总压畸变水平。在发动机稳定试验和试飞中，通常采用在发动机进口安装流场测量耙的直接测量方法获取进口流场数据[9-11]。但由于飞行中机体振动、过载大，测量耙长期装机使用一旦出现结构损坏将严重威胁飞机安全[12]，因此测量耙的流场测量方式并不适用于畸变容限控制技术。HIDEC项目基于飞行控制、大气数据等预测攻角、侧滑角的变化间接表征发动机进口流场畸变的变化[5-6]；HISTEC 项目则采用了基于有限测量的流场畸变估算方法，通过测量少量的内、外壁面动态静压解算发动机进口总压畸变指数[7-8]。HISTEC 项目研究结果表明，基于壁面静压数据的总压畸变重构方法较基于飞行参数的畸变预测方法准确性更高，且该方法仅与发动机进口流场分布有关，重构效果不受配装发动机的影响，所建立的分析模型通用性较强。法国航空航天实验室的Grenson等[13]基于S弯进气道非定常数值仿真流场结果，分别采用神经网络、线性随机估计和二阶随机估计方法，验证了基于壁面静压进行总压畸变流场和畸变指数重构的可行性。国内学者在畸变预测方面也有所研究[14-15]，但鲜有涉及畸变容限控制的畸变实时解算方面的工作。本文以某型飞机进/发试飞数据为基础，采用神经网络方法开展发动机进口总压流场和稳态周向畸变指数的重构研究，并对模型重构准确性和适用性进行分析，以期为国内航空发动机畸变容限控制技术的研发和应用提供参考。

2 建模数据样本

进气总压畸变重构研究以某型飞机进气道/发动机相容性试飞测量数据为基础，包括发动机进口截面稳态压力数据和关键飞行参数。试飞时进气道流场测量采用6耙/30测点的方案，包括30路稳态总压和6路壁面静压。发动机进口稳态压力测点分布如图1 所示，6 支测量耙等角度均布，耙上测点按照等环面原则分布(环面1～5 依次由内至外)；壁面静压测点与测量耙在同一截面等间隔分布。

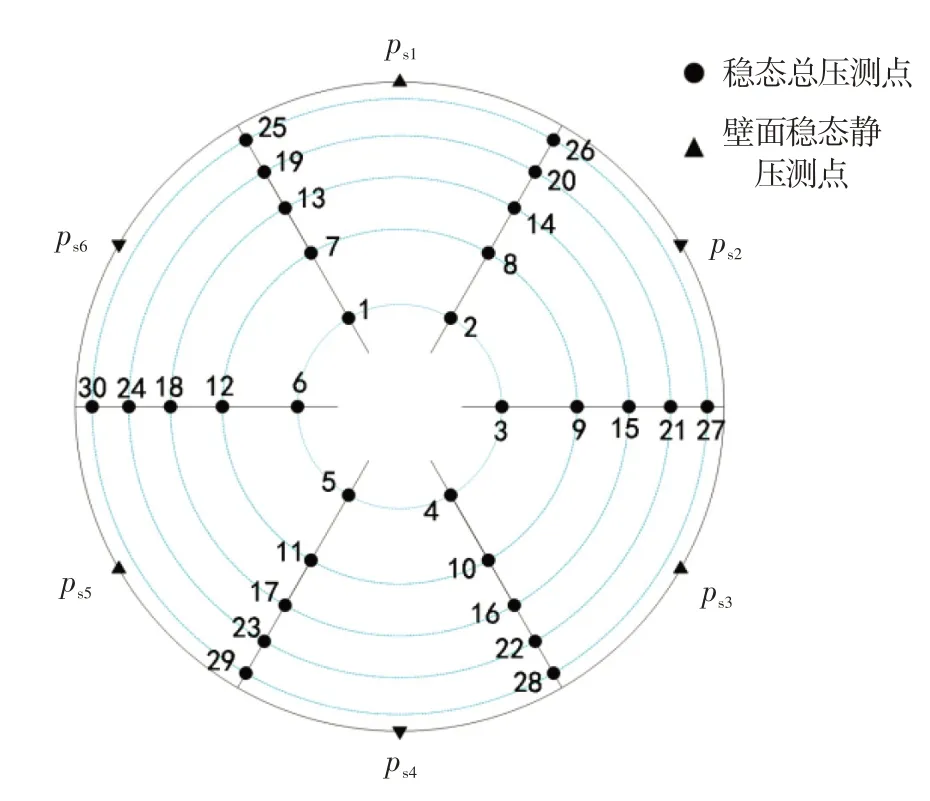
图1 发动机进口面稳态压力测点分布Fig.1 The steady pressure probes layout on the engine inlet face

试飞中稳态压力和飞行参数采样频率为16 Hz，单架次记录数据达到35 000至45 000行，为了在保留数据有效信息的同时降低数据规模和后续计算量，将试飞数据中相近的样本剔除。考虑到本文研究主要以壁面静压作为畸变重构的输入参数，故采用壁面静压作为筛选判断条件。数据分析发现，稳态飞行过程壁面静压波动幅值不大于0.3 kPa，故将0.3 kPa作为数据筛选时的判定标准：若任意一个壁面静压测点在不同时刻记录的数据之差绝对值大于0.3 kPa，则判定这两个样本为不同样本，均存储到筛选样本集中；反之，则认为是相同样本，仅存储最先遇到的样本。采用该方法对所有架次试飞数据进行筛选，总数据样本减少到了13 880 行，有效降低了样本规模。

3 畸变重构的神经网络方法

发动机进口流场畸变重构研究采用BP 神经网络方法，并利用型号试飞数据对神经网络模型进行训练，建立基于壁面静压或组合数据的发动机进口总压畸变重构模型。神经网络模型分别以30 个稳态总压测点数据和稳态周向畸变指数[1]为重构目标，采用不同的输入参数组合，建立了三种BP 神经网络模型，具体见表1。由于实际试飞测量中未测量发动机进口中心点的总压，为了分析中心点总压对畸变重构结果的影响，采用最内环6 个测点的总压平均值等效作为发动机进口中心点总压(以下简称中心点总压)。基于三种神经网络模型结构，分别建立总压流场分布重构神经网络模型和畸变指数重构神经网络模型。所有神经网络模型均采用3层神经网络结构，2 层隐含层神经元数均为30。神经网络训练时将13 880 组样本按比例随机分为三个样本集：70%的样本作为训练样本集，参与神经网络训练；15%的样本作为验证样本集，用于在训练过程中检查模型的泛化能力和判断是否出现过拟合；另外15%的样本作为最终的测试样本集，用于神经网络最终的泛化能力测试。后文中均是在测试样本集上对各神经网络模型进行对比。

表1 神经网络模型输入输出参数Table 1 The neural networks input and output parameters

4 神经网络模型重构结果分析

4.1 总压流场重构分析

图2给出了三种神经网络模型对各自测试样本集30 个总压测点数据的重构误差概率分布。可以看出，神经网络模型重构的总压测点误差呈正态分布，三种模型的重构误差在±正态分布范围内的分布概率分别是97.80%、99.47%和99.67%，模型2 和模型3 较模型1 具有更优重构精度。图3 为测试样本集上三种神经网络模型对30 个测点总压数据重构的均方误差(MSE)。图中，ave为30个测点总压数据重构均方误差的平均值，测点编号参见图1。可以看出，模型1除测点5外各测点重构的均方误差都小于0.9 kPa，平均值小于0.8 kPa；模型2和模型3各测点重构的均方误差均小于0.6 kPa，平均值小于0.5 kPa。在模型1输入参数基础上，模型2增加了中心点总压，使得模型对总压测点的重构准确性较模型1大幅提高；模型3输入参数继续加入攻角、侧滑角后，各测点总压重构均方误差进一步降低。

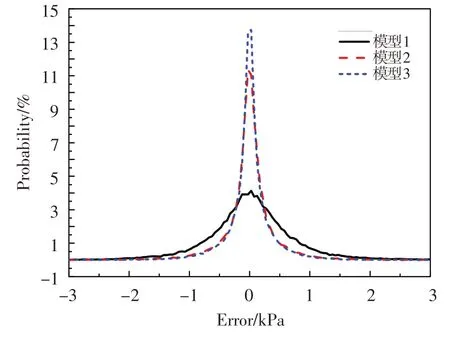
图2 神经网络模型总压重构误差概率分布Fig.2 The probability distribution of total pressure reconstruction error of the neural networks

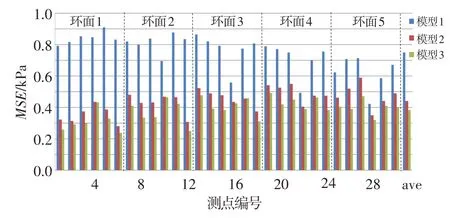
图3 神经网络30个总压测点重构的均方误差Fig.3 The mean square error of 30 reconstructed total pressure probes data of the neural networks

图4给出了三种模型所对应的测量耙各个测量环面(见图1)总压测点重构结果的均方误差平均值。与发动机5环面/30测点的总压空间分布相比，建模所采用的6路壁面静压均位于发动机进口外壁面，仅为周向的一维分布。对于模型1，环面均方误差由外(环面1)至内(环面5)逐渐增大，最外侧环面与壁面静压测点距离最近、相关性最强，重构准确性也最高；壁面静压对发动机进口中心区域流场的表征能力不足。模型2和模型3引入中心点总压后，不仅使得整个测量截面测点的重构均方误差大幅降低，而且还使得各个环面重构均方误差的差异减小。模型2和模型3环面重构均方误差平均值自内环向外环先增大后减小，最大出现在4环面，为中心点总压和外壁面静压综合影响的结果，仍符合环面总压重构准确性随着距离中心点或外壁面的距离的增加而降低。因此，内、外径两个维度的压力数据对于实现畸变流场分布的高精度重构必不可少。

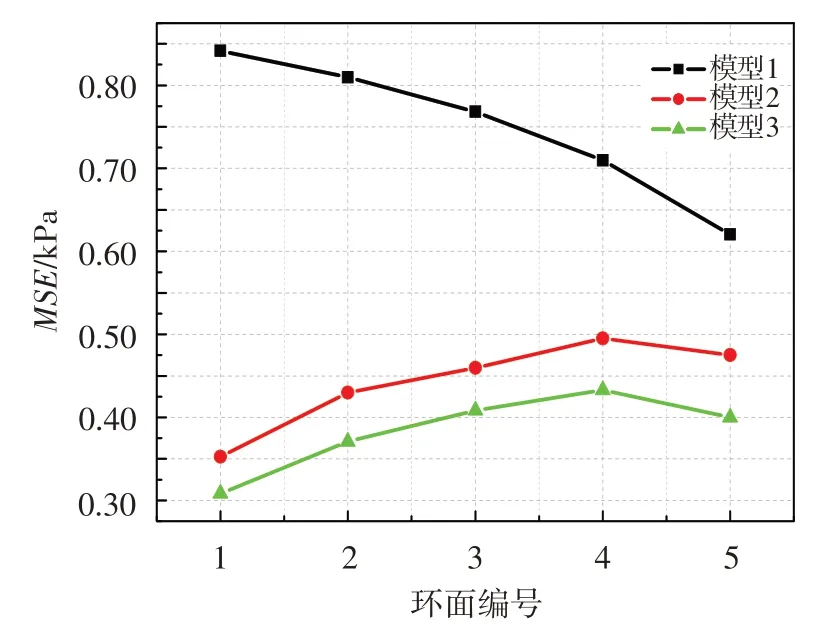
图4 测量耙各个环面总压重构的均方误差平均值Fig.4 The average mean square error of reconstructed total pressure of every ring on the rake

图5、图6分别给出了相同发动机工况下飞机平飞和攻角、侧滑角组合飞行状态，三种神经网络模型对发动机进口30 个测点总压数据重构结果的均方误差平均值和飞行参数的时间历程。可见，对于平飞状态，三种模型的均方误差平均值都较小，模型2和模型3 的重构准确性相当。对于攻角、侧滑角组合飞行状态，当出现较大的负侧滑角时，模型1和模型2 的总压数据重构均方误差平均值明显增大，而模型3 的重构均方误差平均值较小且基本维持稳定。模型1和模型2的重构结果对攻角的变化不敏感，当侧滑角较小时，攻角达到11.0°，其重构结果与模型3 的相当；但模型1 和模型2 对侧滑角较敏感，当侧滑角超过-7.5°时，其重构结果较模型3 的均方误差平均值快速增大。

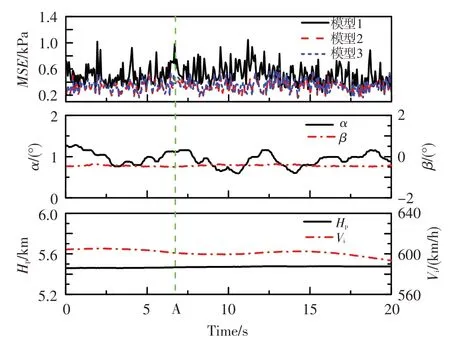
图5 飞机平飞状态神经网络模型的重构结果Fig.5 The reconstruction results of the neural networks in the level flight

图7、图8分别为图5中A时刻和图6中B时刻，根据原始测量数据和三种模型重构数据绘制的发动机进口总压流场分布云图。对于平飞状态，三种模型都可获得较为准确的流场分布，但模型1 重构结果的高压区压力相对偏低。对于攻角、侧滑角组合飞行状态，模型1和模型2的重构结果相似，低压区范围和形状都较原始图谱有较大差别，特别是未能重构出中心区域的低压区；而模型3重构结果的高、低压区范围和形状都与原始图谱吻合良好。综上，对于具有较大攻角和侧滑角的飞行状态，将攻角和侧滑角加入模型输入参数，可显著改善发动机进口流场畸变重构的准确性。

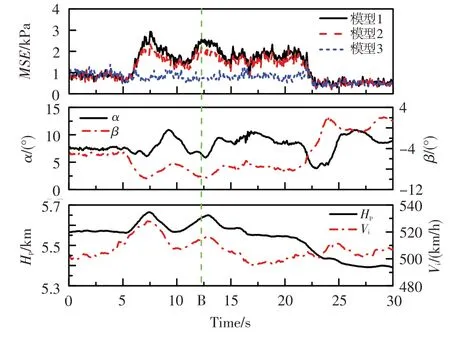
图6 攻角、侧滑角组合飞行状态神经网络模型的重构结果Fig.6 The reconstruction results of the neural networks in the maneuvering flight

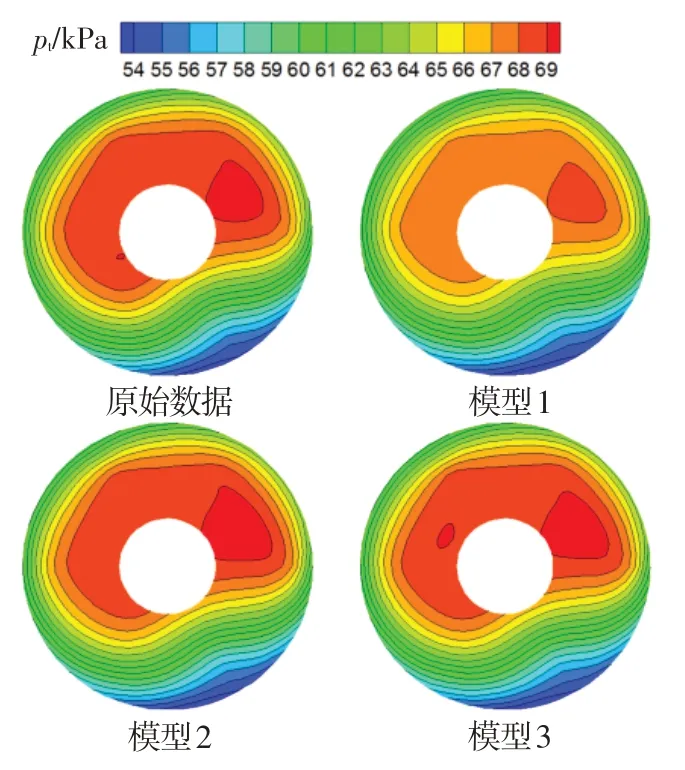
图7 平飞过程发动机进口流场重构结果云图Fig.7 The reconstructed engine inlet flow field in the level flight

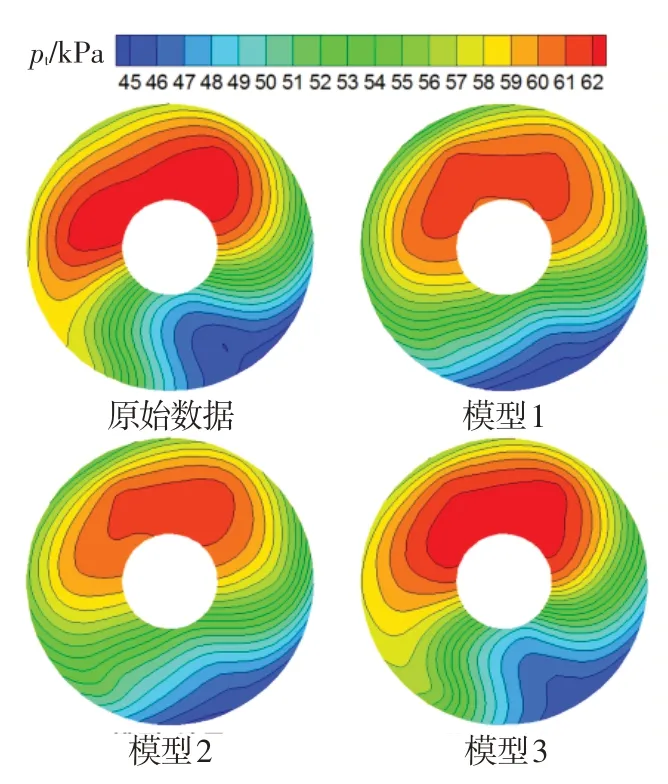
图8 攻角、侧滑角组合飞行过程发动机进口流场重构结果云图Fig.8 The reconstructed engine inlet flow field in the maneuvering flight

4.2 稳态周向畸变指数分析

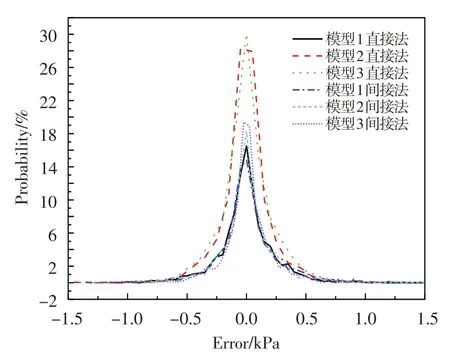
图9 直接法和间接法各模型稳态畸变指数重构结果误差概率分布Fig.9 The distortion index reconstructing error probability distribution of the indirect and direct methods

图10 直接法和间接法稳态畸变指数重构均方误差对比Fig.10 The distortion index reconstructing mean square error comparison of the indirect and direct methods

5 神经网络重构模型适用性分析

为分析训练获得的总压畸变重构神经网络模型的适用性，采用另一型飞机的进气道测量数据验证三种神经网络模型的总压流场分布和畸变指数重构效果。该型飞机与建模数据来源飞机具有相同的进气道结构和布局，但配装发动机不同；进气道流场测量采用了与图1相同的测点布置方案，总、静压测点相对位置也与建模数据来源飞机的相同。

5.1 总压分布重构模型适用性分析

图11为该试验机在11 km高度飞行过程中三种神经网络模型对发动机进口总压分布重构结果的对比，该飞行过程包括平飞、大攻角飞行和侧滑飞行，具有一定的代表性。图中，MSEav为同一时刻30 个测点总压数据重构均方误差的平均值，N1为发动机低压转子转速。可以看出，模型1 的重构均方误差较大且对发动机转速较敏感，当N1大于90%时MSEav达到10 kPa左右；模型3的总压数据重构结果最佳，30个测点的平均均方误差在2 kPa以内，但较图5和图6结果偏大。图12为对应图11中C时刻模型3重构的总压分布与原始数据总压分布的对比。C时刻飞机具有-8°的侧滑角，进气畸变较大。模型3很好地重构出了低压区位置，但低压区范围较原始图谱偏大。由此可得出，模型3 在总压流场分布重构方面对于具有相同进气道结构的飞机有一定的适用性，但与建模飞机发动机进口流场重构结果相比重构准确性偏差。

图11 三种模型总压流场重构结果对比Fig.11 The comparison of 3 neural networks in total pressure reconstructing results

图12 模型3重构图谱与原始数据图谱对比Fig.12 The comparison of the model 3 reconstructed pattern and original pattern

5.2 稳态畸变指数重构模型适用性分析

基于与图11相同的飞行过程数据，对三种神经网络模型采用直接法和间接法进行重构的适用性进行分析。重构均方误差变化如图13 所示，图中MSE1、MSE2、MSE3分别对应模型1、模型2 和模型3的重构均方误差。可以看出，三种模型中模型3的重构结果最好，但均方误差较大(最大达到4%左右)，与图9中建模飞机的测试样本集畸变指数重构结果相比误差较大。对于模型3，采用间接法的重构准确度略优于直接法。综上，对于重构，三种神经网络模型的直接法和间接法对于与建模飞机具有相同进气道结构的飞机的适用性不佳。