基于BP模型的粗粒亚硫酸盐渍土盐胀特性敏感因素研究

张莎莎，刘瑞瑞，王永威

(1. 长安大学 公路学院,陕西 西安 710064； 2. 中交第二航务工程局有限公司技术中心，湖北 武汉 430040)

0 引 言

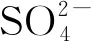
针对粗粒盐渍土盐胀特性的研究，徐学祖等[5]开展了单向冻结试验，揭示了土体盐胀是土体、水分、温度、盐分和荷载的综合作用结果。Wu等[6]研究了恒温下粗粒硫酸盐渍土的盐胀机理、发展过程。包卫星等[7]通过试验对公路工程中存在的粗粒盐渍土的相关盐含量进行了分析和验证。张莎莎等[8-9]按照盐胀五要素对粗粒亚硫酸盐渍土在路用填料方面的应用进行了研究。Zhang等[10-11]采用现场检测和室内试验相结合的方法对冻融及降水条件下粗粒盐渍土路基变形进行了研究。以上研究对于推动整个行业对粗粒盐渍土的认识起到了很大的贡献，也从多个角度实现了含盐量、含水率、初始压实度及上覆荷载对其基本规律的概述，但总体来讲，缺乏针对粗粒盐渍土路基在上述各因素交互作用下变形敏感参数的量化研究。

高江平等[12]在对盐渍土的研究中使用二次回归方程对盐渍土的含水率以及含盐量结合其初始干密度和上覆荷载进行分析，发现可以通过不同因素的调整对盐渍土的性能进行控制。顾强康等[13]以硫酸盐渍土机场地基为例，利用拟合方程进行计算，得到盐胀率与含盐量、压实度及荷载3个因素之间的具体联系。宋启卓等[14]利用人工神经网络推导出细粒硫酸盐渍土与含水率、氯化钠含量、硫酸钠含量、干容重和荷载具体量化关系，得到了相应的计算公式。Wu等[15-16]采用数值方法建立了饱和冻结盐渍土的热-水-盐-力耦合模型。土体颗粒大小、级配使粗粒盐渍土与细粒盐渍土在性质和特征上产生很大的差异，粗粒盐渍土受相关因素的影响与细粒盐渍土也不同。为了合理地使用粗粒亚硫酸盐渍土作为路基填料，需要考虑到各种因素交互作用下对盐渍土性能的影响，并做出相应的调整，探究影响粗粒亚硫酸盐渍土路基变形的敏感参数。

开展工程可控因素交互作用下影响粗粒亚硫酸盐渍土路基盐胀特性的敏感参数研究对于改进其在实际工程的应用具有重要意义。因此，笔者针对细粒土质砾亚硫酸盐渍土、含细粒土砂亚硫酸盐渍土及细粒土质砂亚硫酸盐渍土，在单因素试验结果的基础上，确定多因素交互试验的因素范围。然后，基于BP神经网络模型建立粗粒亚硫酸盐渍土盐胀率与影响因素关系的计算模型，对盐渍土的盐胀率与各因素交互作用之间的具体关系进行了研究，将盐渍土路基发生变形过程中受到不同因素的影响程度进行量化，以调整粗粒亚硫酸盐渍土路基设计的控制指标，从而为路基工程的设计及施工提供指导。

1 试验土样

本文依托伊朗德伊(德黑兰—伊斯法罕)高速铁路项目，由于从现场取土耗费时间长且费用高，结合路基填料含盐量和颗粒级配特征，采用室内人工配制土样的方式开展试验。基于现行的《公路土工试验规程》(JTG E40—2007)[17]，土样根据颗粒粒径组成的不同分为2种，一种是砾类土(细粒土质砾)，另一种是砂类土(含细粒土砂、细粒土质砂)。

考虑到各种影响盐渍土性能的因素，为了将敏感因素的作用集中体现，采取配置易溶盐的方法开展研究，在此基础上对粗粒盐渍土作为路基填料的盐胀特性敏感参数进行研究。以天然素黄土为细粒土填料，将2种土样按实际需求以一定的比例进行混合，可以得到满足级配良好的路基填料(图1)。对试验土样进行击实试验，可得到细粒土质砾亚硫酸盐渍土、含细粒土砂亚硫酸盐渍土及细粒土质砂亚硫酸盐渍土的最大干密度分别为2.22，1.98，2.13 g·cm-3，最佳含水率分别为6.4%，11.0%，8.8%。

图1 土的粒径分布Fig.1 Particle Size Distribution of Soil

2 试验方案

2.1 试验仪器

本文采用高低温试验箱实现对土样温度的控制，其温度范围为-40～60 ℃，使用直径24.5 cm、高度25 cm的柱状筒体开展盐胀试验，土样盐胀率测量采用精度0.01 mm的百分表，为了提高试验的准确度，每组试验都需做平行试验。盐胀试验设备见图2。

图2 试验装置Fig.2 Test Device

2.2 降温试验

对于粗粒盐渍土盐胀率来说，温度是很关键的影响因素，粗粒盐渍土所处区域的温度与季节变化和昼夜更替息息相关。依托工程位于德伊高铁库姆段，结合之前针对亚硫酸盐渍土盐胀率敏感温度范围的研究，统计盐渍土盐胀率变化较为强烈的月份可知，温度变化范围集中在-15～25 ℃之间。在研究过程中利用高低温试验箱对土样降温，降温区间为-15～25 ℃，每次降低5 ℃，每次降温后土样在该温度下维持1 h，降温结束后设定6 h的恒温环境，从而使土样充分盐胀。为了达到土体的盐胀稳定趋势，基于实时监测，含细粒土砂亚硫酸盐渍土盐胀试验-15 ℃稳定16 h。

2.3 单因素作用的盐渍土盐胀试验

根据路基工程相关规范[18]，首先研究盐胀率随含盐量的单因素变化，土样密度为最大干密度值的93%，即93%ρdmax，含水率为最佳含水率ωop，上覆荷载值为0 kPa，亚硫酸盐含量依次设定为0.3%，0.5%，0.8%，1.1%，1.4%，1.7%，2.3%，2.9%，3.5%，4.1%，4.7%；然后进行含水率单独改变的测试，土样密度为最大干密度值的93%，由ωop和ωop±2.2%确定含水率；其次进行初始压实度单独改变的测试，设定土样压实度值为89%，93%，97%；最后开展上覆荷载发生单一变化下盐胀率研究，所设上覆荷载为0，0.276，0.552，0.828 kPa。

2.4 多因素交互作用的盐渍土盐胀试验

对于真实的工程条件，粗粒亚硫酸盐渍土盐胀并非是纯粹单个盐胀因素作用的结果，而是受多个盐胀因素交互作用的影响。在单因素试验结果的基础上，通过正交设计来深入研究当盐胀率受到多个盐胀因素作用的计算模型，通过BP神经网络模型建立盐胀率与其影响因素关系模型。

设置试验因素水平时，主要遵循如下原则：参考盐胀率界限来合理地确定含盐量的实际值[19]，还需符合正交设计(二次回归)标准的要求；选择ωop作为试验土样含水率的基准；选择下路堤有关标准值的93%作为压实度的基础；选择实际的试验条件作为上覆荷载的基准。表1～3详细列出了试验因素水平情况。对于砾类及砂类亚硫酸盐渍土而言，每种土试验因素均为4个，试验水平均为5个，共开展25组不同的试验(每组的平行测试为2或3次)。

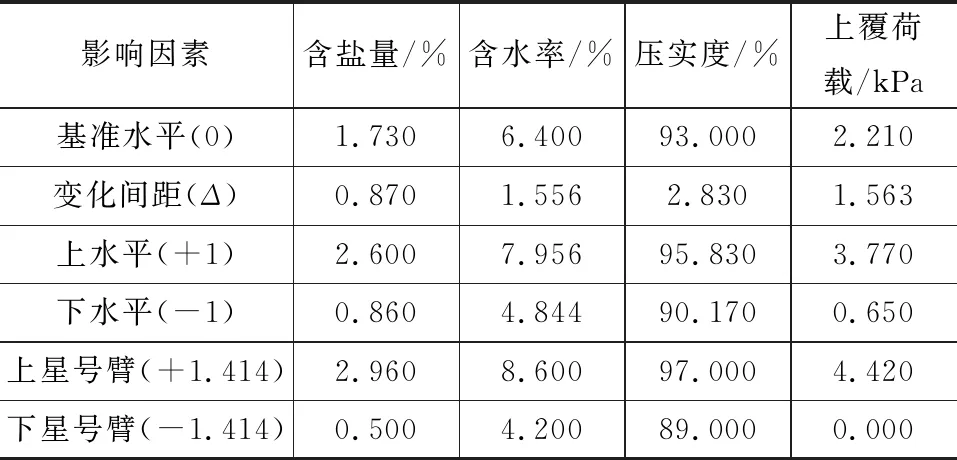
表1 细粒土质砾亚硫酸盐渍土正交试验因素水平Tab.1 Orthogonal Factor Level for Gravel Sulfite Saline Soil

3 粗粒亚硫酸盐渍土盐胀率BP神经网络模型

本文通过建立BP神经网络模型来确定粗粒亚硫酸盐渍土盐胀率与影响因素间的关系。BP算法是从修正性的角度出发，使学习算法具有理论基础[20]，通过相互连接的神经元建立输入和输出变量之间的相关性[21]。与经验和统计方法相比，BP模型的主要优势在于不需要任何有关输入和输出变量之间关系性质的先验知识。本文合理选择了BP神经网络模型(共3层，即输出层、隐含层、输入层)，以促进其结构的有效简化，提升网络训练的效率水平，具体如图3所示。

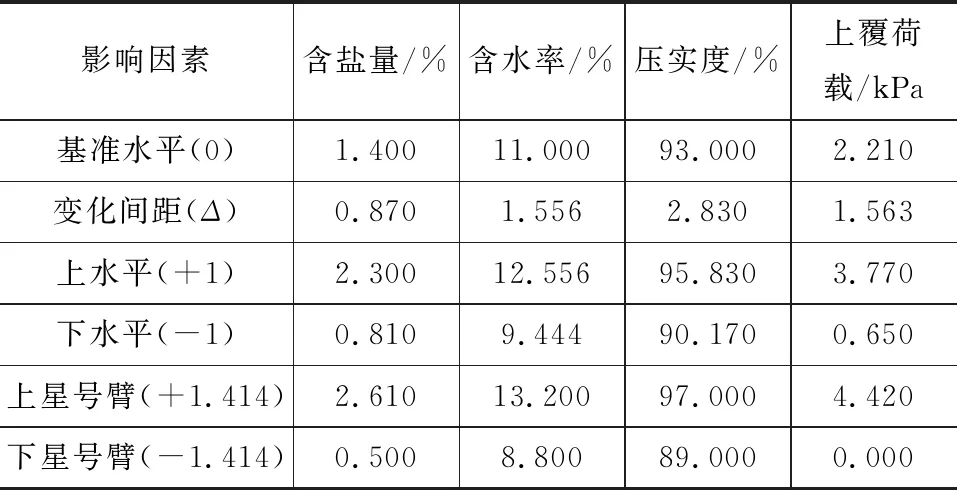
表2 含细粒土砂亚硫酸盐渍土正交试验因素水平Tab.2 Orthogonal Factor Level for Sandy Soil-I Sulfite Saline Soil

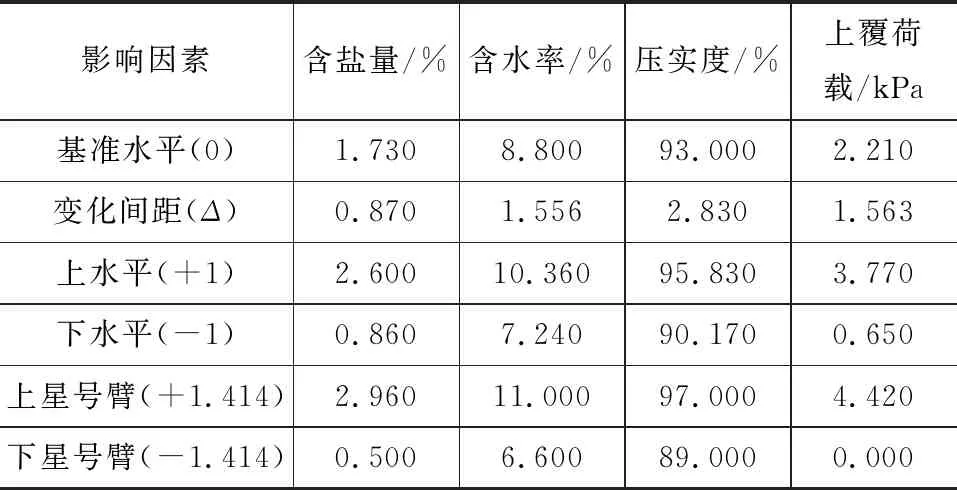
表3 细粒土质砂亚硫酸盐渍土正交试验因素水平Tab.3 Orthogonal Factor Level for Sandy Soil-II Sulfite Saline Soil

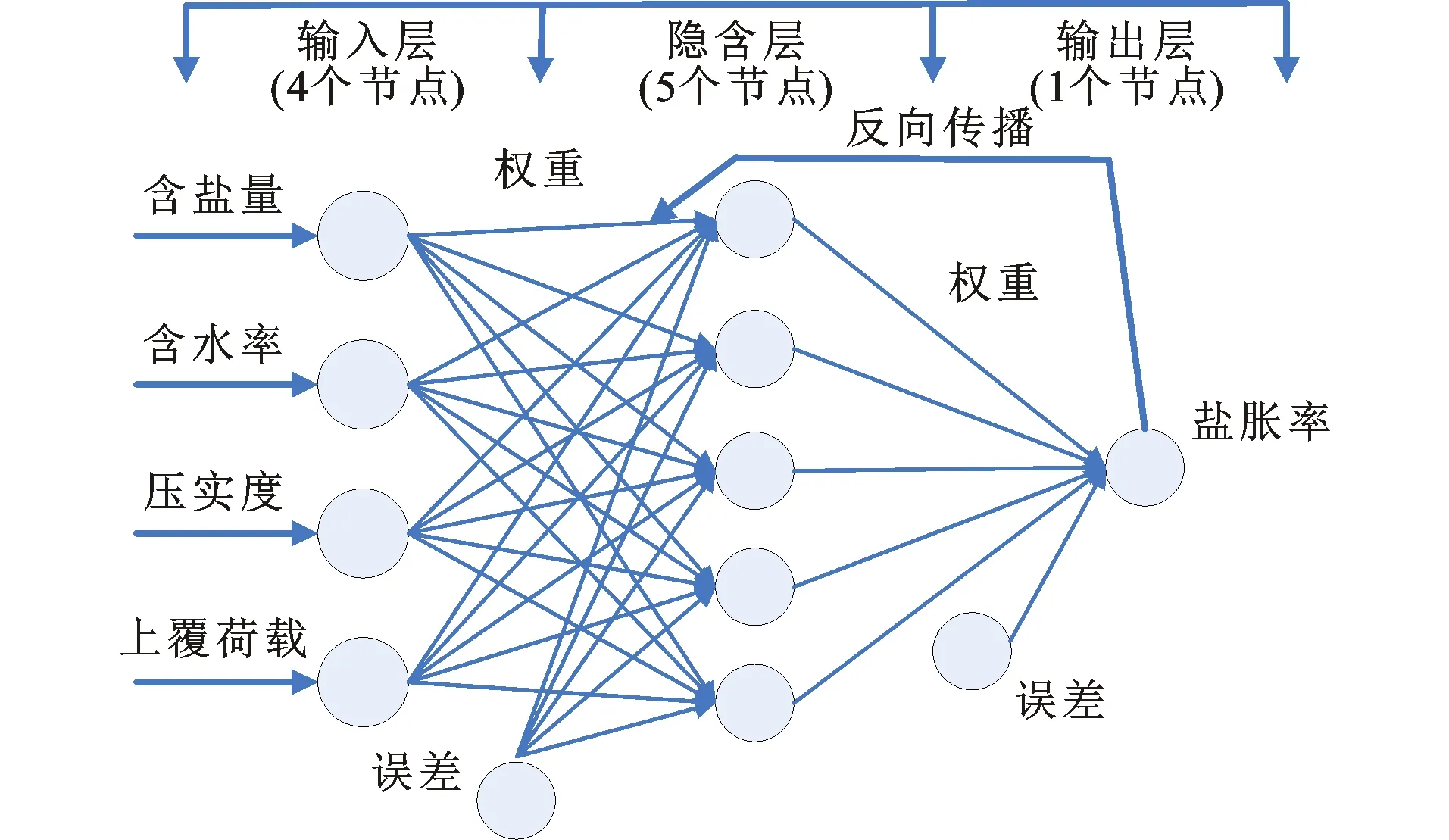
图3 BP神经网络模型的结构Fig.3 Structure of BP Neural Network Model

在对神经网络输入层输入数据时，使用式(1)对输入数据进行归一化处理，将输入的数据变换成[-1，1]区间内的数据。

(1)

式中：Xi为输入数据归一化值；zi为相关的输入数据；zmin，zmax分别为输入数据的最低值和最高值。

对于本文模型，以4×25维的矩阵作为其输入向量，25是具体的组数，4为不同的试验因素(上覆荷载、压实度、含水率以及含盐量)。

在设计BP模型时，需要合理地选择隐含层自身所具有的具体节点数量，若对所得结果的收敛性及准确性进行考虑，那么需使上述节点数提高；若对训练时间如何受到模型隐含层中具体节点数量及网络自身所具有的推理能力的影响予以考虑，那么就需降低上述节点的数量。如要分析某特定领域中应用的相关神经网络，需要对泛化性及精确性进行深入全面分析，再确定上述节点数。对于本文模型，可以通过经验公式(2)来确定其隐含层中的具体节点数，即

(2)

式中：m为隐含层上的具体节点数；n，l分别为输入层及输出层上的具体节点数；α为调整系数，其取值范围为1～10。

根据公式(2)，选择建模隐含层节点数为5个。输出层只有1个节点数，即盐胀率的值。输出结果为归一化后的结果，由公式(3)对输出结果反归一化，即

(3)

式中：YF为反归一化后的盐胀率；Y为BP神经网络归一化后的盐胀率输出计算值；Tmax，Tmin分别为盐胀率最大值、最小值。

本模型选取双曲正切函数tansig作为神经元之间的转移函数，选取线性函数purelin作为输出层转移函数。tansig函数的表达式如式(4)所示。通过MATLAB里的newff函数来生成网络，此外，该函数还可初始化网络阈值及权值。

(4)

4 试验结果及其分析

4.1 单因素作用对粗粒盐渍土盐胀的影响

图4为含盐量变化时粗粒亚硫酸盐渍土的盐胀率变化规律。由图4可知，在提高含盐量之后，与砾类土相比，砂类土盐胀率增长幅度较高。在整个盐胀的过程中，由于具有较好的颗粒级配度，小粒径土样(含细粒土砂和细粒土质砂)可以更为显著地提升盐胀率。此外，参考易溶盐所对应的工程界限值可知[19]，含细粒土砂亚硫酸盐渍土的界限含盐量值约为1.4%，细粒土质砂亚硫酸盐渍土的界限含盐量值约为0.5%，细粒土质砾亚硫酸盐渍土的界限含盐量值约为2.5%。因此，在开展正交试验的过程中，其含盐量都涵盖了上述界限值(表1，2，3)，可见试验方案是合理的。

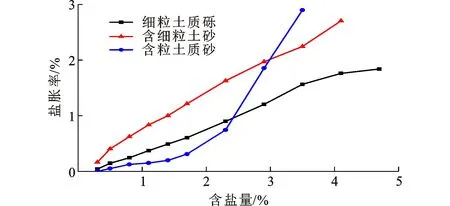
图4 粗粒亚硫酸盐渍土盐胀率随含盐量变化Fig.4 Variation of Salt Expansion Rate with Salt Content for Coarse-grained Sulfite Saline Soil

图5为含水率变化时粗粒亚硫酸盐渍土的盐胀率变化规律。由图5可知：亚硫酸盐渍土盐胀率受到含水率的影响与易溶盐含量高低相关，当易溶盐含量为0.5%时，盐胀率会因含水率提高而提升；当易溶盐含量为2.6%时，盐胀率会因含水率提高而降低[22]。

图5 粗粒亚硫酸盐渍土盐胀率随含水率变化Fig.5 Variation of Salt Expansion Rate with Water Content for Coarse-grained Sulfite Saline Soil

盐胀率受到含水率的作用机制比较复杂，其中初始压实作用效果将会受到盐渍土本身和易溶盐间作用机制的影响，含水率随着盐胀率的变化所发生的改变也将有不同的规律[23]；此外，当土体级配存在差异时，上述变化也存在特定的界限含水率及含盐量值。在重视路堤防水的同时，也要做好最佳含水率的有效控制。

图6为初始压实度变化时粗粒亚硫酸盐渍土的盐胀率变化规律。由图6可知，在提高初始密度值后，盐胀率也会相应地上升，主要原因是提高了土体的密度值以后会降低土体的孔隙率，由此极大地提高了盐胀率[24]。

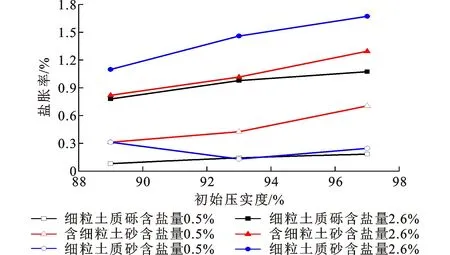
图6 粗粒亚硫酸盐渍土盐胀率随初始压实度变化Fig.6 Variation of Salt Expansion Rate with Initial Compaction for Coarse-grained Sulfite Saline Soil

图6中含盐量为0.5%的细粒土质砂亚硫酸盐渍土在提高初始压实度时其盐胀率却降低，主要是由于在降温的最初阶段存在结晶盐，对土体的结构形式产生了破坏[24]，粗粒土所具有的大孔隙结构会造成其盐胀变化方面的不稳定特征。

图7为上覆荷载变化时粗粒亚硫酸盐渍土的盐胀率变化规律。由图7可知，盐胀过程会受到上覆荷载较为强烈的抑制作用。

图7 粗粒亚硫酸盐渍土盐胀率随上覆荷载变化Fig.7 Variation of Salt Expansion Rate with Overburden Load for Coarse-grained Sulfite Saline Soil

4.2 多因素交互作用的粗粒盐渍土盐胀试验结果

多因素交互作用的粗粒亚硫酸盐渍土的最终盐胀率试验结果如图8所示。从图8可知：在试验因素水平设定条件下，细粒土质砾亚硫酸盐渍土的最大盐胀率为1.602%，最小盐胀率为0.255%；含细粒土砂亚硫酸盐渍土的最大盐胀率为1.663%，最小盐胀率为0.562%；细粒土质砂亚硫酸盐渍土的最大盐胀率为1.881%，最小盐胀率为-0.054%。所设定的因素水平符合相关要求[22]。

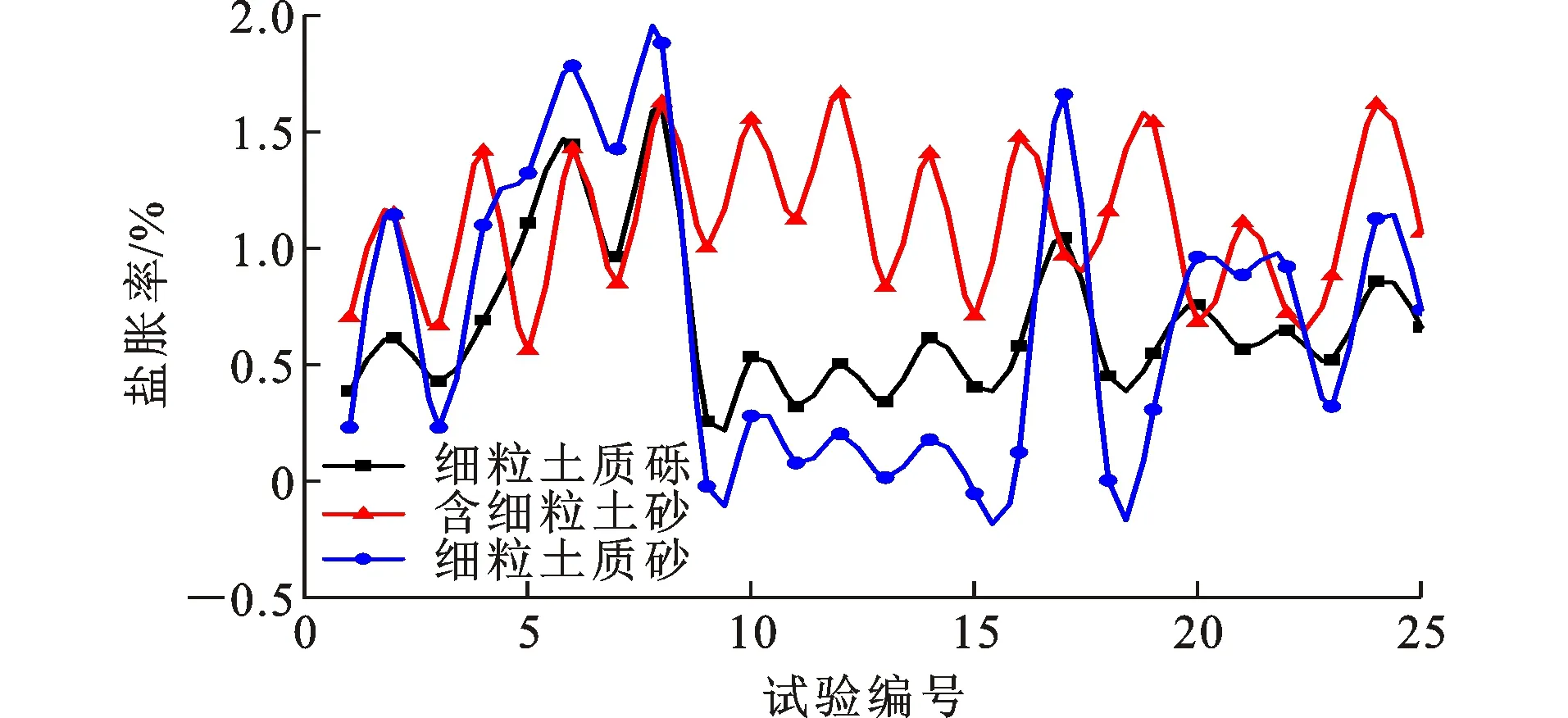
图8 多因素交互作用下盐胀率试验结果Fig.8 Salt Expansion Test Results Under Interaction of Multiple Factors

4.3 细粒土质砾亚硫酸盐渍土盐胀率与其影响因素计算模型

基于BP模型，细粒土质砾亚硫酸盐渍土的盐胀率方程为

aLS=-0.484 8X1+0.939 2X2+0.021 5X3-

1.263 7X4-4.127 6

bLS=-1.739 3X1-0.516 2X2-1.918 3X3+

2.362 3X4-0.114 3

cLS=-0.661 5X1-0.345 4X2+1.573 4X3+

1.133 8X4-0.141 7

dLS=1.484 2X1+1.622 9X2+1.2576X3+

0.861 4X4+0.911 2

eLS=3.601 7X1+0.300 2X2-0.465X3+

2.190 9X4+2.209 4

(5)

式中：X1，X2，X3，X4分别为归一化后的含盐量、含水率、压实度、上覆荷载；R2为决定系数。

图9详细地展示了细粒土质砾亚硫酸盐渍土通过式(5)得到的盐胀率计算值与实测值的差值。可以发现它们较为接近，最大差值约为0.238%，建立的计算模型是稳定的。

图9 粗粒亚硫酸盐渍土盐胀率计算值与实测值的差值Fig.9 Difference Between Salt Expansion Rate Calculated Values and Measured Values for Coarse-grained Sulfite Saline Soil

4.4 含细粒土砂亚硫酸盐渍土盐胀率与其影响因素计算模型

基于BP模型，含细粒土砂亚硫酸盐渍土的盐胀率方程为

aHY=0.245 7X1-1.103 9X2-0.440 5X3-

2.916 1X4-2.918 4

bHY=1.541 5X1+1.694 3X2-0.563 6X3+

0.260 8X4-2.158 7

cHY=-1.845 7X1+1.457 5X2-0.088X3+

1.549 2X4-0.091 1

dHY=0.378 9X1-1.355 2X2-1.170 3X3+

3.358 1X4-0.363 3

eHY=1.010 4X1-2.562 9X2+1.089X3+

1.254 6X4+2.698 7

(6)

图9详细地展示了含细粒土砂亚硫酸盐渍土通过式(6)得到的盐胀率计算值与实测值的差值。可以发现它们较为接近，最大差值约为0.346%，建立的计算模型是稳定的。

4.5 细粒土质砂亚硫酸盐渍土盐胀率与其影响因素计算模型

基于BP模型，细粒土质砂亚硫酸盐渍土的盐胀率方程为

aSY=-0.310 3X1-3.711 8X2-1.938 5X3+

3.949 6X4+2.000 2

bSY=2.058 9X1-1.125 0X2+0.386 8X3-

1.086 9X4-0.744 1

cSY=1.623 3X1-5.239 3X2-0.369 8X3-

1.205 0X4+2.791 1

dSY=-4.229 6X1+3.786 2X2+0.097 9X3-

0.224 1X4+3.014

eSY=4.328 4X1+5.308 9X2-0.889 9X3-

3.331 3X4+3.040 5

(7)

图9详细地展示了细粒土质砂亚硫酸盐渍土通过式(7)得到的盐胀率计算值与实测值的差值。可以发现它们较为接近，最大差值约为-0.216%，建立的计算模型是稳定的。

5 影响因素权重讨论

当含盐量在本文试验设定的范围、含水率为最佳含水率、压实度为最大干密度的93%、上覆荷载为0 kPa时，由BP神经网络模型得到的盐胀率随含盐量的变化趋势如图10所示。从图10可知，在提高含盐量之后，盐胀率也会随之提升，而砾类亚硫酸盐渍土含盐量提高到某一程度后，盐胀率随含盐量的增大速率变缓甚至减少。这是因为随着含盐量的增加，结合土中水形成更多的结晶盐，因此盐胀率随含盐量的增加而增大，但是当含水率一定时，随着含盐量的增加而形成过饱和溶液，结晶盐的析出反而减少，盐胀率增大将不再明显甚至呈下降趋势。

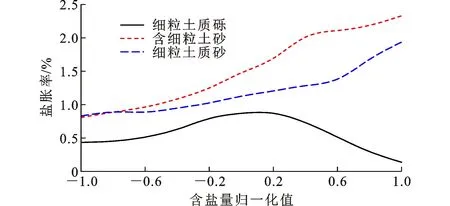
图10 盐胀率随含盐量变化趋势Fig.10 Trend of Salt Expansion Rate with Salt Content

当含盐量为试验范围中间值、含水率为最佳含水率 2.2%、压实度为最大干密度的93%、上覆荷载为0 kPa时，由BP神经网络模型得到的盐胀率随含水率变化趋势如图11所示。当含盐量为试验范围中间值、含水率为最佳含水率、压实度为最大干密度的93%、上覆荷载为0～4.42 kPa时，由BP神经网络模型得到的盐胀率随上覆荷载变化趋势如图12所示。由图12可以发现，当上覆荷载提高之后，盐胀率逐渐减小，也就是前者具有对盐胀过程的抑制作用。

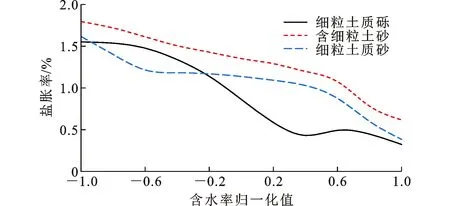
图11 盐胀率随含水率变化趋势Fig.11 Trend of Salt Expansion Rate with Water Content

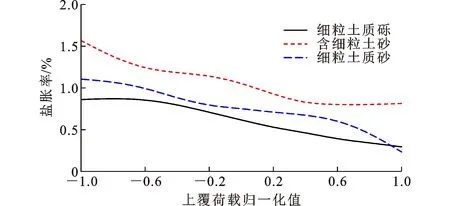
图12 盐胀率随上覆荷载变化趋势Fig.12 Trend of Salt Expansion Rate with Overburden Load

盐胀率的影响因素包括了初始压实度，然而在BP模型中却没有体现出来。究其原因，认为试验土样具有较高的最大干密度值，在当前试验所设压实度条件下(从89%～97%)，具有较小的干密度区别，此外，从参考所进行的单因素试验可以发现，当提高压实度值时，盐胀率的变化不太明显，起到的作用较小。

由盐胀率影响因素权重分析可知，下述交互作用相对显著，包括含盐量与含水率、上覆荷载与含水率、上覆荷载与含盐量[25]。根据所采用的BP模型研究可知，对于砾类亚硫酸盐渍土而言，其含盐量与含水率、上覆荷载与含水率的交互作用达到显著性水平，对于砂类(细粒土质砂)亚硫酸盐渍土而言，其含盐量与含水率、上覆荷载与含盐量的交互作用达到显著性水平[14]，取压实度为最大干密度的93%，上覆荷载为试验范围中间值2.21 kPa，含水率与含盐量交互作用对盐胀率影响程度如图 13所示。同理可得，上覆荷载与含水率的交互作用、上覆荷载与含盐量的交互作用对盐胀率影响程度分别如图14，15所示。

由图13可知，当含水率一定时，含盐量越大，对盐胀的促进作用越强。由图13(a)可知，当含盐量一定时，砾类亚硫酸盐渍土盐胀率随含水率增加的变化规律呈现先减小后增大的趋势；由图13(b)可知，砂类(细粒土质砂)亚硫酸盐渍土盐胀率随含水率的变化趋势与含盐量的高低相关，含盐量较低时盐胀率会因含水率提高而逐渐提升，含盐量较高时盐胀率会随着含水率提高而发生显著的降低。这是因为交互作用的存在，使得盐胀率随含水率的变化规律在其他因素取不同值时，表现了不同的变化规律。

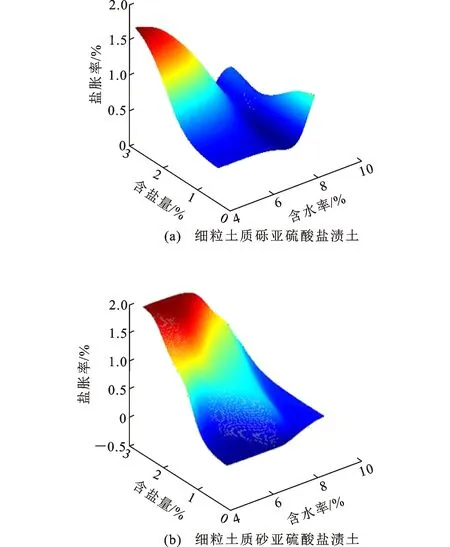
图13 含盐量与含水率的交互作用对盐胀率的影响Fig.13 Influence of Interaction Between Salt Content and Water Content on Salt Expansion Rate

从图14可知，当上覆荷载较小时，砾类亚硫酸盐渍土盐胀率随含水率的减小速率大于上覆荷载较大时。从图15可知：如果含盐量保持不变，在比较高的上覆荷载作用下，将会提升抑制盐胀的效果，当该荷载值为3 kPa及其以上时，盐胀现象大为降低；如果保持上覆荷载值不变，那么提高含盐量会促进盐胀过程。

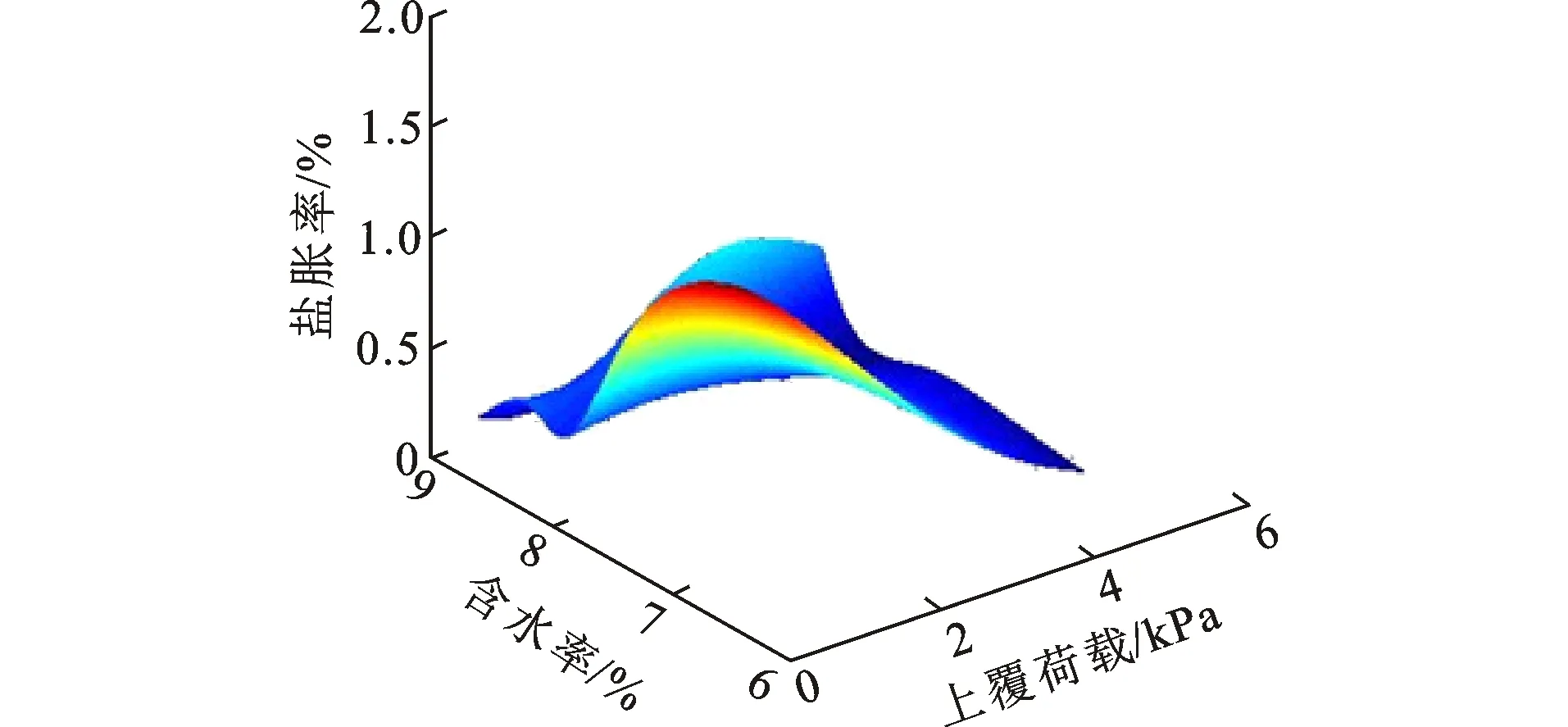
图14 细粒土质砾亚硫酸盐渍土含水率与上覆荷载的交互作用对盐胀率的影响Fig.14 Influence of Interaction Between Water Content and Overburden Load on Salt Expansion Rate for Gravel Sulfite Saline Soil

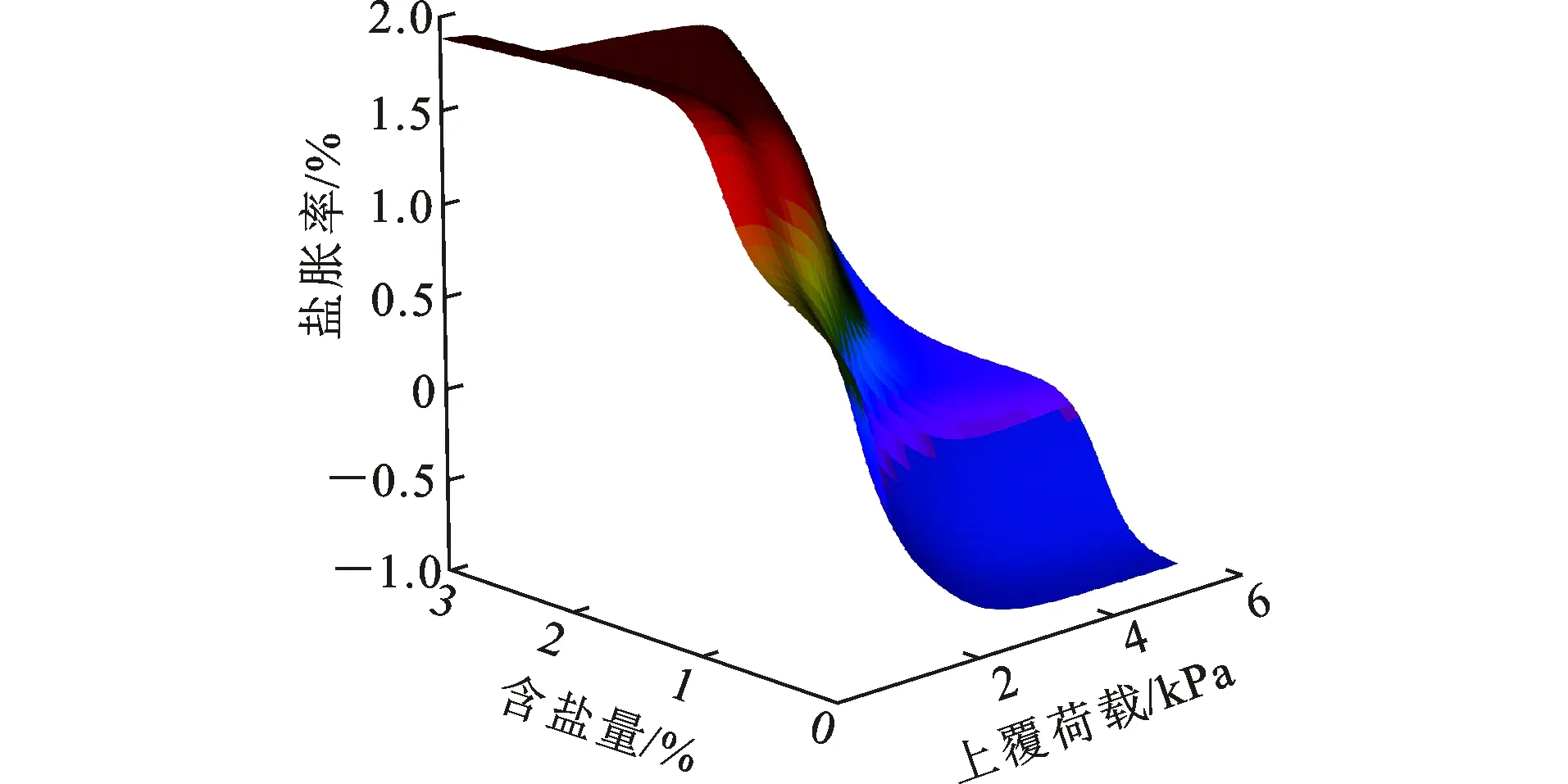
图15 细粒土质砂亚硫酸盐渍土含盐量与上覆荷载的交互作用对盐胀率的影响Fig.15 Influence of Interaction Between Salt Content and Overburden Load on Salt Expansion Rate for Sandy Soil-II Sulfite Saline Soil

由上可知，与上覆荷载和含水率相比，含盐量对盐渍土盐胀率影响作用较为明显，这与盐胀率影响因素权重相一致，同时也验证了BP模型的正确性。

6 结 语

(1)基于单因素改变条件下的盐胀试验，采用二次回归正交试验设计，通过BP模型建立了砾类(细粒土质砾)亚硫酸盐渍土盐胀率计算模型和砂类(含细粒土砂、细粒土质砂)亚硫酸盐渍土盐胀率计算模型。

(2)根据BP模型，砾类亚硫酸盐渍土的含盐量与含水率、上覆荷载与含水率的交互作用显著，砂类(细粒土质砂)亚硫酸盐渍土的含盐量与含水率、上覆荷载与含盐量的交互作用显著。

(3)在工程应用中，上覆荷载对粗粒亚硫酸盐渍土(含细粒土砂)盐胀率大小的抑制作用需要结合颗粒级配方面的情况来展开分析，细粒土含量起到的影响作用比较明显。同时，在路基防排水措施良好的情况下，从影响粗粒亚硫酸盐渍土盐胀特性的敏感参数分析结果可以看出，易溶盐和荷载所占比例最大，水的影响较小。在进行相关路基设计时，建议采用重型路面结构以抑制盐胀率的增长，合理利用粗粒亚硫酸盐渍土作为路基填料。