框架-嵌入式墙体结构抗震性能研究

魏文晖，马中原，朱 东，楚 尚

(1. 武汉理工大学 道路桥梁与结构工程湖北省重点实验室，湖北 武汉 430070； 2. 中南电力设计院有限公司，湖北 武汉 430071)

0 引 言

框架-嵌入式墙体结构是装配式工业建筑中的新型结构形式，在柱的侧面预留墙板插槽，将预制混凝土墙板自上而下插入凹槽，内嵌式安装[1]，如图1所示，采用此种形式，整个施工过程仅需吊车，无需现场支模，墙体既安装方便，又具有较大抗侧刚度，可替代柱间支撑，特别适用于类似电力系统换流站阀厅结构等对墙体有一定刚度要求的工业建筑,中国已有部分阀厅结构采用此种内嵌式混凝土防火墙取代现浇式混凝土防火墙，如杨柳变电站、登胜变电站等工程[2]。框架-嵌入式墙体结构中，由于墙板与柱间连接的特殊性，若按装配式剪力墙结构进行分析，会过高估计结构的抗侧刚度；按常规框架填充墙进行计算，将忽略嵌入式墙体对结构抗侧刚度的贡献，对于换流站阀厅这类不对称结构[3]，将低估扭转变形对整体结构的不利影响，降低结构的安全性。因此，确定墙板对阀厅结构抗震性能的影响是一个亟需解决的问题[4]。

图1 嵌入式墙体结构体系Fig.1 Embedded Wall Structure System

目前，国内外学者对装配式框架和装配式剪力墙结构研究较多[5-12]，但对装配式框架-嵌入式墙体结构的抗震性能研究较少,且大多为钢框架结构，黄宇星等[13]提出了设立柱凹槽插入墙板的方式来取代外挂式和侧连式的墙板，但对该类结构的抗震性能未深入研究，杨晓杰等[14]采用ANSYS分析软件探究了嵌入式墙板-钢框架结构的抗震性能，分析显示嵌入式墙体显著改变了结构的振型；高松召[15]基于等效斜撑模型提出了等效多杆弹塑性模型，利用此计算模型研究了某钢结构住宅的抗震性能，结果表明嵌入式钢板对整体结构抗侧刚度的贡献不可忽略；Su等[16]对某采用内嵌式墙体的高层混凝土结构进行了有限元分析，得出表面内嵌式墙体的存在提高了结构的抗侧刚度，减小了顶点位移。夏军武等[17]对带M型限位槽的蜂窝夹芯内嵌板钢筋混凝土框架及空腹钢筋混凝土框架进行了低周往复试验，结果表明内嵌墙板与框架的协同作用可提高弹性阶段框架的抗侧移能力。李国强等[18]通过水平静力及低周反复加载试验，研究了横排外挂、竖排外挂和竖排内嵌3种连接方式下预制ALC墙板钢框架结构的性能，试验结果显示，相较于外挂的ALC墙板，内嵌式ALC墙板对整体结构的刚度和承载力的提升较大。

上述学者对嵌入式墙体的发展做出了巨大贡献。预制装配式混凝土墙体已成为装配式建筑中最常用的围护体系[19]。外墙体主要可分为外挂式、内嵌式和内叶承重夹芯式3类[20]，对于内嵌式的墙体，以往大多采用轻质砌块砌筑的形式，随着建筑装配化的推进，少量建筑开始采用内嵌墙板的形式。目前，内嵌式墙体结构多见于钢框架，实际工程中，内嵌墙体与钢框架主体结构的连接形式主要为U型卡连接[21]、GT螺栓连接[22]、ADR节点连接[23]等形式，此外，内嵌式墙体亦在钢框架-钢筋混凝土结构体系中有所应用，如美国西尔玛、巴西Porto Vleho等。本文通过振动台试验，对钢筋混凝土框架-嵌入式墙体结构的抗震性能展开研究，以期为此类新型结构的设计提供参考。

1 试验概况

试验以某嵌入式装配防火墙阀厅结构为研究原型，选取具有代表性的中间相邻两榀框架结构单元，结构单榀跨度为8.8 m，相邻两榀间距为6.9 m，共2层，总层高为11.8 m，将荷载等效为质量后其总质量为331 682 kg，混凝土强度等级为C50，纵向受力筋采用HRB400级热轧钢筋，箍筋及框架梁腰筋采用HPB235级热轧钢筋。

1.1 试件设计

按照相似理论确定模型相似常数，以此作为模型设计依据。本次设计选取长度、混凝土弹性模量和等效密度相似常数为基本相似常数，依据似量纲分析法[24]计算模型相似常数。根据振动台尺寸，确定几何相似常数为1∶3。考虑到振动台的承载力，选择降低结构配重，增大台面输入水平加速度，将模型设计为非满配重的形式。虽然非满配重形式会改变柱构件的轴压比，但本试验重点研究的是嵌入式墙板对结构的影响，柱的竖向轴力对整体结构试验结果的影响较小，且不会改变实际结构的破坏模式。采用此种方法，求得的振动台模型相似常数如表1所示。

表1 模型相似常数Tab.1 Model Similarity Constant

根据以上相似关系及承载力等效的原则，模型几何尺寸如图2(a)，(b)所示。模型各层梁柱尺寸及配筋均相同，柱截面如图2(c)所示，梁截面如图2(d)所示，嵌入式墙板尺寸及配筋如图2(e)所示。

图2 模型尺寸及配筋示意图(单位:mm)Fig.2 Schematic Diagram of Model Size and Reinforcement (Unit:mm)

试验模型选用普通混凝土制作，底座通过高强螺栓与台面连接，配重采用2根普通钢筋混凝土梁来施加，通过长螺杆和固定铁板连接在框架梁上。所有构件混凝土等级均为C20，梁柱构件与插板构件同批浇筑，实测其立方体抗压强度标准值为21.7 MPa，轴心抗压强度为14.5 MPa，纵筋采用HRB400级钢筋，箍筋采用采用HPB300级钢筋，模型钢材性能实测结果见表2。

表2 钢材性能试验结果Tab.2 Test Results of Steel Performance

混凝土达到一定强度后，即可进行试件的吊装和定位，如图3(a)所示。随后，使用桁车将嵌入式板吊起沿柱内侧槽口依次插入，为方便装配，墙板与柱凹槽两侧各预留了5 mm的间隙，并对墙体与凹槽之间的间隙采用木楔进行加固处理，模型吊装拼接完成后如图3(b)所示。

图3 构件装配图Fig.3 Assembly Diagram of Component

1.2 试验方案

本文选取典型的3条真实强震记录，包括El Centro波南北向、Taft波东西向和天津波南北向，并对其进行截取与压缩处理，截取原波时间间隔为0.02 s，压缩波输入时间间隔为0.006 s，数据采集时间间隔为0.02 s。

本次试验使用日本东京测器公司(TML)生产的位移拾振器SDP-300D及加速度拾振器ARF-A测量位移及加速度数据，通过TMR-300小型多通道数据采集系统收集记录模型在地震作用下的加速度响应及位移响应。试验前在振动台上对各拾振器进行一致性标定。加速度测点布置在台面、一层顶及二层顶，共计3个，位移测点布置在在台面和一层顶，共计2个。

为了详细掌握不同地震作用下结构的动力响应情况，本次试验采用分级加载的方式输入地震波，地震波沿模型长边方向输入，在每一个工况前后对结构施加白噪声激励以获得不同烈度地震作用下结构的自振特性变化情况，从而判断结构的刚度降低程度，实际试验加载工况见表3，g为重力加速度。

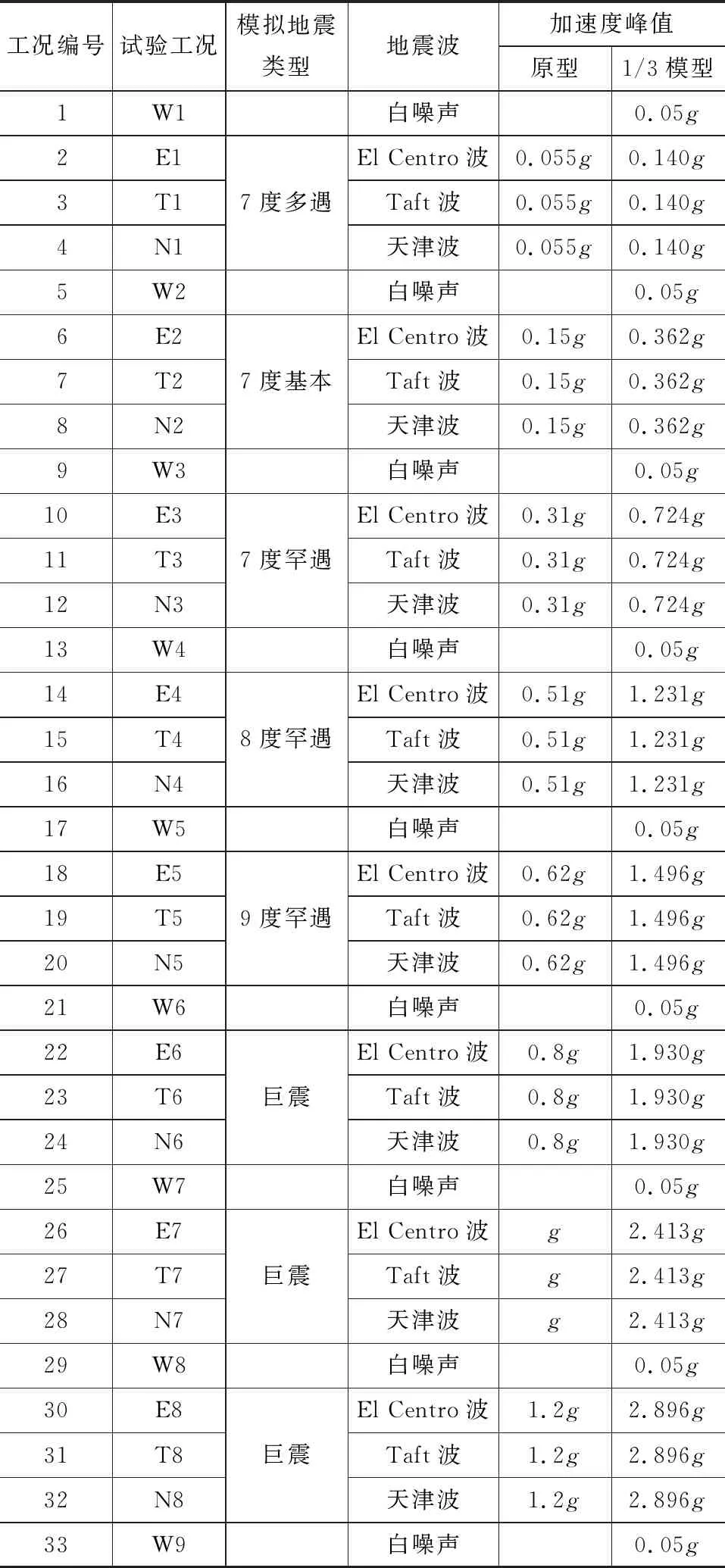
表3 试验工况Tab.3 Test Conditions

2 试验结果及其分析

在地震波工况正式加载之前对结构进行白噪声扫频以确定其自振频率。试验正式开始后以同一地震烈度下的3个不同地震波工况及之后的白噪声扫频为1组进行试验加载，每组工况加载完成后观察结构试验情况。

2.1 试验现象

7度多遇烈度下，模型结构表面没有发现任何裂缝出现，表明整个结构仍处于弹性阶段；7度基本烈度下，在一层梁端首先出现细微的自梁下边缘向上发展的竖向裂缝，如图4(a)所示；7度罕遇烈度下，在墙板中央首次出现竖向裂缝，如图4(b)所示；8度罕遇烈度下，一层柱顶端出现水平裂缝，柱凹槽外边缘、柱脚破环更加严重，如图4(c)所示；9度罕遇烈度下各块墙板出现垂直于加载方向的不规则错动，相对振动反应较为明显；继续加载至试验结束，模型正面框架、背面框架以及框架侧面上、一层的梁端均有裂缝，一层柱身裂缝较为密集，其中一层柱顶端最严重，框架柱凹槽外边缘破坏严重，如图4(d)所示大块混凝土脱落，内嵌式墙板墙角压坏，裂缝向墙板中部延伸，墙板中部裂缝加深，上下墙板参差交错。

图4 各阶段试验现象Fig.4 Experimental Phenomena at All Stages

2.2 动力特性

图5 半功率法计算结构阻尼比Fig.5 Calculation of Structural Damping Ratio by Half Power Method

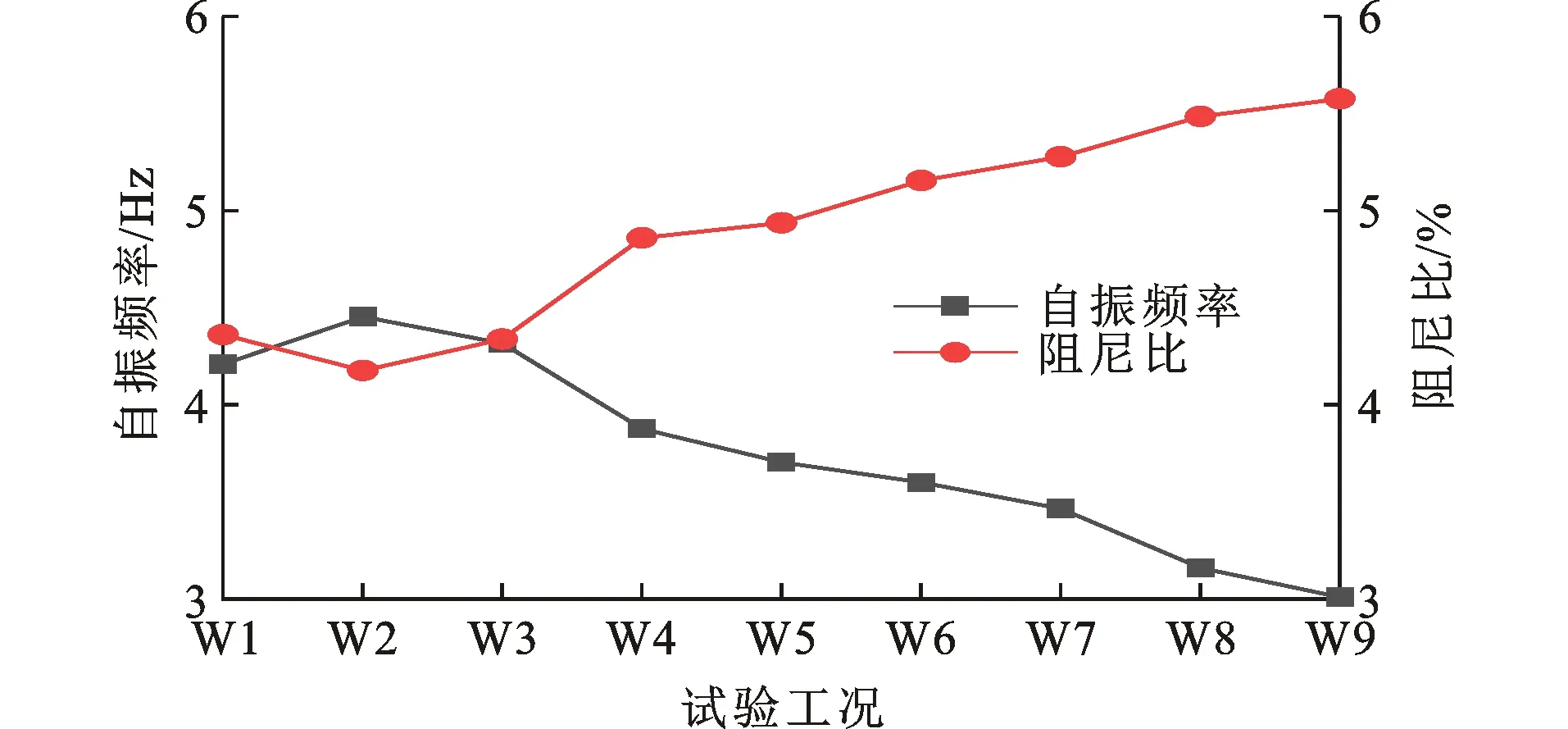
图6 模型自振频率和阻尼比变化Fig.6 Model Natural Frequency and Damping Ratio Variation

本次试验中，结构的自振频率先增大后减小，工况W2时自振频率最大，达到了4.45 Hz左右，这是由于加载前期，振动使得框架主体发生细微变形，内嵌式墙板与主体框架连接的更加紧密，使得整体结构刚度略有增加。随着模型刚度的变化，阻尼比呈现出先减小后增加的趋势，初始状态下，模型处于弹性阶段，阻尼比约为4.35%。随着加载的进行，模型刚度逐渐增大，而阻尼比则下降至4.17%，继续加载，模型的阻尼比逐渐上升，表明随着加载的进行结构产生了不可逆的塑性变形且塑性的逐渐发展使得模型损伤不断加剧，试验中表现为新裂缝不断产生，原有裂缝继续延伸发展，加载至试验后期甚至出现混凝土脱落等现象。

2.3 模型加速度反应

在多遇烈度、设防烈度和罕遇烈度等各试验阶段，对振动台试验模型分别输入El Centro波、Taft波和天津波3种地震波，通过记录各层加速度时程数据以绘制时程曲线。限于篇幅，选取部分工况的台面及各层加速度时程曲线，如图7所示。由图7可知：模型顶层加速度反应时程与模型底座加速度反应时程相比，加速度峰值呈放大现象；两者峰值变化趋势基本上是一致的。

图7 El Centro波7度多遇烈度下台面及各层加速度时程Fig.7 Acceleration Time History of Platform and Each Layer Under 7 Degree Frequent Intensity of El Centro Wave

模型各层加速度放大系数如图8所示。由图8可知，模型结构各楼层加速度放大系数峰值会随着加载的进行而增大，这是由于加载前期结构刚度逐渐增大的缘故。随着加载的进行，模型结构在持续加载下，损伤不断积累，导致刚度下降，使得加速度放大系数随着地震作用的增强而逐渐减小。

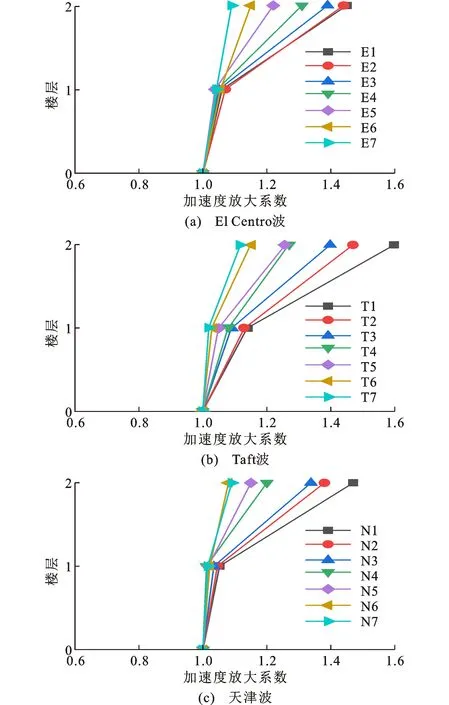
图8 模型各层加速度放大系数Fig.8 Acceleration Amplification Coefficients of Each Layer of Model

2.4 模型位移反应

各层位移包络图如图9所示。由图9可知，随着输入地震波振幅的增大，模型结构的最大位移不断增大，位移曲线整体上呈剪切型，而不是剪力墙结构常见的弯曲型变形及框架剪力墙结构的弯剪型变形。据此可知，尽管由于嵌入式墙板的存在使得结构的自振特性发生了较大变化，但由于墙板分块插入，墙板之间可以沿着加载方向相互错动，嵌入式墙板仍不能像剪力墙那样作为结构的主要抗侧力构件参与受力。

图9 模型各层位移包络图Fig.9 Displacement Envelope Diagram of Each Layer of Model

对于钢筋混凝土框架结构，在多遇烈度地震作用下，其弹性层间位移角不应超过1/550。在罕遇烈度地震作用下，钢筋混凝土框架薄弱层弹塑性层间位移角不应超过1/50。试验模型在各工况下层间位移角最大值如表4所示。

由表4可以看出，随着加载的进行，整体上结构的层间位移角逐渐增大，在多遇烈度下，各楼层的层间位移角均未超过弹性层间位移角限值。即使在9度罕遇地震烈度下，结构的一层层间位移角也满足弹塑性层间位移角限值1/50的要求。由此可见，框架-嵌入式墙体结构具有良好的抗震性能，即使在较大的地震作用下，结构也不会产生过大的水平位移，满足规范中对弹塑性变形的要求。

表4 模型各楼层层间位移角最大值Tab.4 Maximum Value of Inter Story Displacement Angle of Each Floor

3 结 语

(1)在试验初始阶段，框架结构的变形使得墙板与主体框架连接更为紧密，内嵌式墙板使得结构整体刚度有所增强，结构的自振频率随着地震动强度的增大而略有增加。地震动强度继续增大时，结构的自振频率则不断下降。

(2)在7度基本烈度下, 结构一层梁端首次出现竖向裂缝。至加载结束后，一层框架梁端、一层框架柱脚处裂缝较为密集，内嵌式墙板四角混凝土出现不同程度的破坏，框架柱插墙凹槽处混凝土损坏较为严重，但墙柱之间仍保持可靠的连接，结构仍保持较好的整体性。

(3)通过比较结构各层层间位移可以看出，结构一层的弹塑性层间位移出现突变，为结构的薄弱部位。根据现行抗震设防规范，结构薄弱层处弹性及弹塑性层间位移角值在规范限值以内，据此判定此类结构抗震性能良好，结构基本满足7度设防要求。

(4)振动中各块墙板相对振动反应较为明显，应对墙角采取构造措施加固，并在墙板顶端增设压梁；为充分利用墙板与整体结构相对振动时对地震能量的耗散效果，设计时可在内嵌式墙板与框架柱凹槽之间增设缓冲带；由于嵌入墙板与柱轴线不在同一直线上，各柱承受了一定的扭矩，应通过合理布置结构平面，防止柱产生扭转，或考虑增加抗扭构造配筋及进行柱抗扭配筋的验算，提高柱的抗扭承载力。