变形钢筋与混凝土黏结性能数值模拟与计算

易伟建，罗先明

(湖南大学 土木工程学院,湖南 长沙 410082))

0 引 言

钢筋与混凝土之间的黏结是指两者的相互作用和力的传递，黏结强度是两者之间最大的相互作用力。在正常使用条件下，黏结强度影响裂缝的形成与发展以及结构的变形。在承载力极限状态，黏结使锚固在混凝土中的钢筋充分发挥强度，黏结性能还影响塑性铰区域的转动能力。

为了研究各种参数对黏结性能的影响，常用短锚固长度的中心拉拔试验[图1(a)]，其中，τm为整根钢筋平均黏结强度，τmax为局部最大黏结应力。将试验得到的拉拔力除上钢筋锚固在混凝土中的表面积得到平均黏结强度，同时以钢筋滑移量和该平均黏结强度作为钢筋和混凝土黏结关系的基本本构属性。由此得到的黏结-滑移关系只适用于锚固长度比较短的情况。锚固长度较长时[图1(b)]，黏结应力的分布不均匀，局部黏结应力可能达到平均黏结应力的2倍[1]。

图1 短锚固试验和长锚固试验Fig.1 Short and Long Anchor Test

黏结锚固作用在握裹层混凝土中引起的应力状态十分复杂，但是如果主要考虑单根钢筋的锚固问题，则可以先分析沿锚固长度方向钢筋和混凝土的纵向应力、应变以及界面上的黏结应力，而握裹层混凝土中应力场的问题可在沿纵向(锚固长度方向)变化的规律解决后求得。因此，单根钢筋的锚固问题可以简化为一维问题进行考虑。

对于长锚固的普通中心拉拔构件，以整根钢筋为对象进行分析，滑移量s(x)为关于距离钢筋加载端位置x的函数(图2，其中F为拉力，τ为黏结应力，σs为钢筋应力，σc为混凝土应力)。s(x)可以通过沿钢筋长度方向上不同位置的2种材料应变差的积分来表示，即

图2 钢筋和混凝土的应力状态Fig.2 Stress State of Rebar and Concrete

(1)

式中：εs(x)为钢筋在距离加载端x处的应变值；εc(x)为混凝土在x处的应变值；x0为自由端位置；S0为自由端滑移，即钢筋的刚体位移。

若钢筋处于弹性状态，那么应力σs便可以用Esεs来表示，其中Es为钢筋的弹性模量，同样，混凝土应力、应变也可以通过其弹性模量Ec进行换算。

在长锚固中心拉拔构件中，对隔离体单位钢筋进行受力分析，由黏结力在微段上沿钢筋圆周表面积的力和钢筋应力换算出截面上受到的拉力平衡，不难得到黏结应力τ与钢筋应力σs的关系[2]为

(2)

式中：D为钢筋直径。

由隔离体单位钢筋混凝土的受力分析可知

Asdσs+Acdσc=0

(3)

式中：As为钢筋截面面积；Ac为混凝土截面面积,即构件总截面积减去钢筋截面面积。

设As/Ac为ρ，钢筋弹性模量与混凝土弹性模量比值Es/Ec为n，则式(3)可以简化为

dεc=-nρdεs

(4)

将式(4)代入式(2)并对x求导得

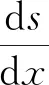
(5)

将式(5)两边同时乘以钢筋弹性模量Es，便得到钢筋应力σs与滑移s的关系，再代入式(3)得到钢筋滑移与黏结应力的关系，即

(6)

式(6)为二阶微分方程，若知道钢筋的本构关系和黏结-滑移本构关系以及边界条件，可通过数学方法得到实际受力过程中钢筋的应力分布及黏结应力的分布。

文献[3]通过假定钢筋本构和黏结-滑移本构均为线性的，通过数学解析法在不同的边界条件下求解出了不同的黏结应力分布。Tastani等[4]通过拟合的线性黏结-滑移关系，根据自由端钢筋应力为0、加载端钢筋应力为荷载所对应的钢筋应变得出了钢筋应变的分布表达式，还定义了当滑移大于本构关系中的最大滑移后对应的锚固区域为混凝土塑性阶段，即黏结屈服段，当应变超过钢筋应力-应变本构中的屈服应变后对应的锚固区域为钢筋塑性阶段。从而在纵向上建立了一比较合理的黏结应力、钢筋应变分布。

在目前已知的黏结-滑移本构模型中，均为非线性关系且存在下降段，这样非线性二阶微分方程不能通过解析法直接求出应力-应变及滑移的数学表达式，只能通过近似方法求得数值解。

Ciampi等[5]通过假定在某个步长内黏结应力是线性分布的，得出了3种边界条件计算黏结应力分布的递推程序，且在每一个步长收敛完成后对钢筋应力-应变本构及钢筋混凝土黏结-滑移本构关系进行更新，从而得到了钢筋锚固在各种情况下及各种加载历程下的整体黏结和滑移响应，其计算的本质方法为数学上的试射法，但若人为地对锚固钢筋边界条件进行干预，所得到的结果具有一定的局限性。

Filippou[6]基于沿钢筋锚固长度上的黏结应力分段线性分布函数，提出了在往复荷载激励下钢筋锚固响应的简化模型。该方法将钢筋沿锚固长度方向上分成三部分，即中间部分约束良好的钢筋仍然保持弹性，而在两端的钢筋由于应力较大或有应变渗透的影响单独进行考虑。这样可以非常快速地迭代收敛。此外，该方法避开了黏结-滑移本构关系，取而代之的是黏结应力近似线性分布函数，无须单独去定义不同约束条件下不同的黏结-滑移本构关系。

徐有邻[7]通过假定在某个步长内黏结应力是均匀分布的，得出了一般条件下由钢筋计算黏结应力分布的递推程序，并且加入了黏结应力的位置函数，使得黏结应力分布与实际情况更加贴切。

钢筋与混凝土之间的黏结对结构受力有十分重要的作用，但若从结构整体上使用复杂三维精细有限元分析黏结问题是不现实的。因此，建立出一套便捷、高效、准确的简单方法是很有必要的。使用简单的方法时黏结-滑移本构关系或黏结应力分布始终无法绕开，其关键在于黏结-滑移本构的准确性。黏结-滑移本构受到各种因素的影响，目前现有的设计规范中，给出的黏结-滑移本构模型仅能运用于特定条件。考虑到上述情况，本文推演了递推迭代算法，并通过比选采用一种适用于迭代计算且考虑完善的本构关系，对现有部分试验结果进行了验证，基于迭代计算结果对中国及部分国家的锚固长度设计公式进行了比较分析。

1 递推迭代方法及本构选用

1.1 递推迭代方法

一般情况下，钢筋与混凝的黏结-滑移本构及钢筋本构往往不是线性的，有的还是分段函数。无法通过数学方法直接得到解析解，仅能通过数学上的有限差分等方法求出数值解，即沿钢筋长度方向上一系列节点的解。一般采用等距节点，通过递推方法算出钢筋应力分布、滑移分布、黏结应力分布。然后利用边界条件使用迭代的方法找出每一步荷载的真实解。递推迭代方法如图3所示，将钢筋与混凝土沿着锚固长度方向上分割成等距的1～n份，每一份长度为Δx。

图3 递推迭代方法Fig.3 Recursive Iterative Method

为了方便黏结-滑移本构关系的选用，一般加载过程为给定滑移量，迭代求出钢筋应力。由于假定在细分的每一微段钢筋上黏结应力分布是均匀的，因此4个递推式如下：

(1)黏结-滑移本构:τ(i)=f1[s(i)]

f1表示黏结-滑移本构关系函数，通过钢筋的变形计算得到当前位置的滑移，并将其作为函数的自变量代入黏结-滑移本构关系，便得到与之相对应的黏结应力。

得到当前位置的钢筋应力及黏结应力后，通过平衡方程计算得到下一微段上的黏结应力，钢筋表面的黏结应力使钢筋应力沿其长度衰减。

(3)钢筋本构：εs(i+1)=f2[σs(i+1)]

f2表示钢筋应力-应变关系的反函数。每得到一新位置上的钢筋应力时，便需要通过得到的应力求得钢筋的应变，并将每一微段上的应变记录下来。一般材料本构关系以应变来表达应力，但由于数值分析的需要，须将其改写成应力表达应变的形式。

本文中钢筋应力-应变本构关系采用双线性本构模型，如图4所示，其中ks，ksy分别为钢筋进入屈服之前和进入屈服之后的斜率，fu，fy分别为钢筋极限强度和屈服强度，εu，εy分别为钢筋极限应变和屈服应变。

图4 钢筋双线性本构关系Fig.4 Bilinear Constitutive Relationship of Bar

钢筋本构关系方程如下：

弹性段

(7)

塑性段

(8)

在该步的转化中，忽略掉了混凝土应变对整体滑移的影响，因为相对于钢筋的应变来说混凝土的应变可以忽略不计[5-6,8-9]，且若要考虑混凝土的应变，需对该位置的片状混凝土进行受力分析，很显然混凝土的受力是不均匀的，且还会随着混凝土承压面的变化而发生变化。因此该数值方法忽略掉了混凝土应变的影响。

在程序中使用4个数组分别记录下计算过程中沿钢筋长度方向上的钢筋应力σs、应变εs、滑移s以及黏结应力τ。

开始进行迭代时，σs(1)为假定钢筋极限强度fu的一半，并通过二分法找出满足边界条件的解，该解即为钢筋此时荷载条件的应力值，并以此计算出此时钢筋受到的荷载。

(5)收敛条件判定

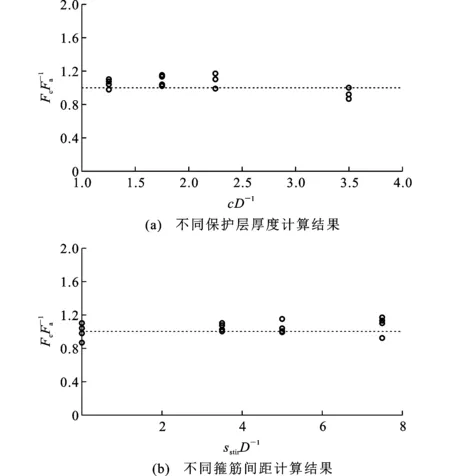
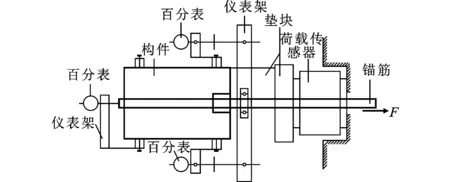
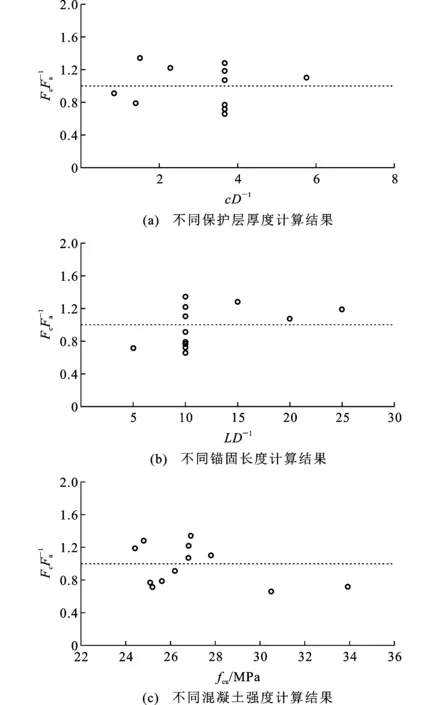
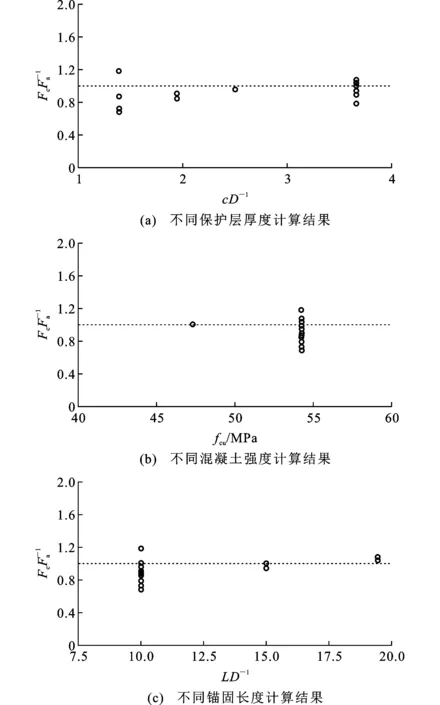
定义Δτ，Δσ为某一微量，即程序允许的误差限制，程序中取0.001。若满足下列2项条件，则当前位移下的程序收敛：①当i

其他情况则根据当前钢筋应力和黏结应力判断出假设的初始钢筋应力是过大还是过小，进而确定二分法下一次迭代的上下限，往复操作直到假设的钢筋应力能满足上述2项条件为止，便完成了当前滑移量的迭代计算，再开始重新迭代计算下一滑移量，每一滑移量计算完成时，计算并记录下钢筋应力对应的荷载，这样便能够得到加载的荷载-位移曲线，递推迭代流程见图5。

图5 递推迭代流程Fig.5 Recursive Iterative Process

应当注意的一点是，在使用该方法进行计算时，忽略掉了混凝土变形的影响，而在中心拉拔试验构件中，部分构件会不可避免地出现纵向裂缝，这种情况下，若采用单一的黏结-滑移本构关系进行计算，则会出现明显的偏差，即无法考虑混凝土裂缝的影响。该递推算法采用一种考虑了多种锚固条件变量下的黏结-滑移本构来处理这种情况，即使用不同的黏结-滑移本构来考虑混凝土纵向裂缝。

1.2 黏结-滑移本构关系的选用

以往学者对钢筋和混凝土之间的黏结-滑移本构关系进行了大量的研究，在早期的研究中，黏结-滑移曲线往往是指构件平均黏结应力和构件端部(加载端、自由端)滑移的关系图，而不是真正意义上的黏结-滑移本构关系(局部黏结应力-滑移关系)。本构关系受到众多因素的影响(混凝土强度、约束条件、钢筋直径等)，早先的本构关系考虑不够完善，因此本文中选取了近期提出的2种本构关系，和设计规范中的本构关系进行比较分析。

1.2.1 中国规范[10]黏结-滑移本构

中国规范给出的黏结-滑移(τ-s)曲线如图6所示，规范给出了曲线特征点的参数值，其中下标cr，u，un，r分别代表劈裂、峰值、卸载、残余段特征点。

图6 中国规范黏结-滑移本构曲线Fig.6 Bond-slip Constitutive Curve of Chinese Standard

规范采用四折线描述钢筋与混凝土之间的黏结-滑移特征，形式较为简单，但其局限于约束良好的构件，无法表达各种约束条件下及往复荷载构件的响应。

1.2.2 CEB-FIP[11]规范黏结-滑移本构

CEB-FIP规范参考诸多学者的研究成果，给出了如图7所示的本构关系及相关参数取值，其中τb为黏结应力，τbmax为约束良好的黏结应力峰值，τbu,split,2为带箍筋但约束不够发生劈裂破坏的峰值黏结应力，τbu,split,1为完全无约束发生劈裂破坏的峰值黏结应力，τbf为残余黏结应力，s1(s2)，s3分别为τbmax，τbf对应的滑移量。除此之外，还通过考虑钢筋屈服、横向钢筋约束应力、纵向裂缝和往复荷载作用的影响，规定了4个参数对本构进行相应的折减。CEB-FIP规范的本构关系较为完整，考虑了多种因素的影响，但其本构分为3组，分别用于描述拔出破坏、劈裂破坏以及完全无约束试件的本构关系，这使得在进行分析时需要人为对试件破坏模式进行判断。

图7 CEB-FIP规范的黏结-滑移本构曲线Fig.7 Bond-slip Constitutive Curve of CEB-FIB Code Standard

1.2.3 文献[12]黏结-滑移本构

Lin等[12]基于Eligehausen等[13]的本构模型，保留其上升段[式(9)]，采用了新的下降段，下降段基本形式与上升段相一致，仅指数系数α从正值变成了负值，并引入公式(10)所示的约束系数K，通过试验数据标定后加到其本构的下降段。

(9)

(10)

式中：c为混凝土保护层厚度；ρst为配箍率；λ为配箍影响系数。

该本构关系考虑了箍筋对其下降段的影响，且使用方便，但其在转折点处不连续，有限元分析时易不收敛，针对往复荷载亦无法使用。

1.2.4 文献[14]黏结-滑移本构

Wu等[14]考虑到现有本构(分段形式)的不连续性容易导致有限元分析中的不收敛现象，以式(11)的函数形式进行回归分析，得到了关于各类影响黏结强度的连续函数表达式。

(11)

采用系数K表示约束对黏结强度的贡献，即

K=Kco+33Kst

(12)

(13)

式中：Kco为保护层厚度的约束系数；Kst为箍筋项约束系数。

该函数形状随着系数B和Q的变化而发生变化，且适用于描述钢筋与混凝土的黏结-滑移本构，并通过对数据库进行回归分析，对B和Q的值进行了标定。

B，Q系数标定结果为

(14)

(15)

对比上述4种本构模型，文献[14]的本构模型不仅考虑的参数更全，且为一连续函数，在迭代计算的过程中易收敛，因此本文迭代计算的黏结-滑移本构选定为该方法计算的本构模型。

2 试验验证

以往学者为了研究钢筋与混凝土之间的基本黏结性能，通过大量的短锚固中心拉拔/梁式试验得到了一系列黏结应力-滑移的本构关系，为验证本文中所采用本构关系的正确性及该模拟方法对于长锚固构件的适用性，将以往试验结果与迭代递推计算的结果进行比较验证，具体试验数据见表1。

表1 试验数据Tab.1 Test Data

续表1

2.1 文献[12]试验

为研究混凝土被动约束对黏结性能的影响，Lin等[12]对不同保护层厚度及不同箍筋配置的共计16个构件进行了拉拔试验。采用2根锚固钢筋同时进行拉拔，将钢筋置于混凝土块体角上，为避免边缘局部混凝土压碎，采用梁端加载方式，分别在加载端和自由端采集滑移信息，并在压板处设置相应的无黏结段，避免其压应力对黏结区域产生影响，构件尺寸及加载方式如图8所示，通过构件基本信息和式(14)，(15)可以算出文献[14]方法本构关系的2个关键参数，便得到了该构件的具体本构关系。利用该本构关系和第1.1节中的递推迭代算法便可得到构件的荷载-位移响应，得到的最大荷载即为该锚固构件的最大承载力。

图8 构件边界及加载方式(单位:mm)Fig.8 Component Boundary and Loading Method (Unit:mm)

计算结果与文献[12]试验结果的比较如图9所示，其中，Fc为计算所得到的破坏荷载，Fa为试验所得到的破坏荷载，图9(a)，(b)分别代表破坏荷载比值随着保护层厚度c及箍筋间距sstir变化而改变的趋势，可见两者的比值较为稳定且介于0.87～1.17。

图9 计算结果与文献[12]试验数据比较Fig.9 Comparison of Calculation Results with Experimental Data in Literature [12]

2.2 文献[15]试验

为了研究高强度钢筋(HRB500)的材料力学性能及其在混凝土中的黏结锚固性能，设计了72个中心拉拔试件(每一相同参数下设置6个)，该试验采用中心拉拔加载(图10)，即约束住加载端混凝土面，使用穿心千斤顶顶住夹在钢筋顶端的锚具，升千斤顶从而实现拉拔荷载F，属于比较常见的中心拉拔加载方式。在加载端设置一定距离的无黏结段从而排除加载端约束对黏结区域的影响。设置了不同混凝土强度等级及不同钢筋直径和保护层厚度的变量。同样使用文献[14]方法计算本构基本参数后进行迭代计算，将试验结果均值与使用递推迭代计算的结果进行对比，对破坏荷载数值进行比较。

图10 构件加载方式Fig.10 Component Loading Method

试验设置的主要变量为保护层厚度、锚固长度以及混凝土强度，图11(a),(b),(c)分别代表这3种变量的计算结果与试验结果的比值，比值介于0.66～1.34。虽说离散性高于文献[12]的试验数据，但观察其原始数据发现，对于相同构件，试验所得到的结果离散性较大，且考虑到混凝土强度的离散性，该结果仍在可接受范围内，与文献[12]数据不同的是，该数据包含了长锚固构件，如果说短锚固构件其作用是用于验证所采用本构关系的正确性，那么长锚固构件可以用来验证该递推迭代方法的正确性。

图11 计算结果与文献[15]试验数据比较Fig.11 Comparison of Calculation Results with Experimental Data in Literature [15]

2.3 文献[16]试验

针对600 MPa钢筋与混凝土黏结锚固性能问题，采用与文献[15]类似的加载方式，即棱柱体中心/偏心拉拔试验方法，对63个直锚构件进行拉拔试验，分析600 MPa钢筋黏结锚固性能的主要影响因素，包括混凝土强度、保护层厚度、锚固长度、配箍率。使用本文算法对试验数据进行计算并比较(仅挑选发生锚固破坏构件)，结果如图12所示，可见各类锚固条件下的计算值与试验值吻合良好，计算结果与试验结果的比值介于0.68～1.18。

图12 计算结果与文献[16]试验数据比较Fig.12 Comparison of Calculation Results with Experimental Data in Literature [16]

2.4 文献[17]试验

为了研究约束条件、保护层厚度、钢筋直径等对黏结性能的影响，通过梁式加载方式对8组搭接构件进行了试验，加载方式如图13所示，其中，P为荷载，h为构件截面高度，h=200 mm，w为构件截面宽度，w=150,20 mm，Ls为锚固长度。通过两点加载，在梁中间部位给予一纯弯矩段，使搭接的2根钢筋产生相互拉力。计算结果如图14所示，计算结果与试验结果的比值介于0.86～1.20，在可接受范围之内。

图13 文献[17]构件加载方式(单位:mm)Fig.13 Component Loading Method in Literature [17] (Unit:mm)

图14 计算结果与文献[17]试验数据比较Fig.14 Comparison of Calculation Results with Experimental Data in Literature [17]

3 规范与递推迭代方法计算锚固长度的比较

3.1 各国规范锚固长度的比较

选取4种规范(GB 50010—2010[10]，CEB-FIP[11]，ACI 318-19[18]，ACI 408R-03[19])的受拉钢筋锚固长度设计公式进行比较，具体设计公式及其参数如表2所示。

表2 目前受拉钢筋锚固长度设计公式Tab.2 Current Design Formula of Anchorage Length of Tensile Reinforcement

3.2 各因素对规范锚固长度的影响

通过试验结果验证递推迭代算法与本构关系的适用性后，由于其计算的高效性，可以对各种影响锚固性能的参数进行变量分析，将各类参数的标准值代入公式进行计算比较。

3.2.1 平均黏结强度与锚固长度的关系

一般来说，短锚固试验的黏结应力分布基本均匀[20]，随着锚固长度的增长，其黏结应力分布将不再均匀，说明对于长锚固构件，沿钢筋长度方向上的所有微段不能同时达到黏结-滑移本构的峰值[8]。因此，若在长锚固构件中按照短锚固构件所定义的平均黏结强度τu进行计算，其平均黏结强度必然会呈现下降的趋势。使用本文的递推迭代方法计算出平均黏结强度随着锚固长度变化的趋势，并与规范比较，结果如图15(a)所示，其中归一化按照中国规范构造参数进行设置。可以看到，递推迭代计算结果和美国ACI 408R-03规范以及CEB-FIB规范经验公式的平均黏结强度均随着锚固长度的增加而减小，趋势大致一致。中国规范和美国ACI 318-19规范及CEB-FIB规范设计公式的平均黏结强度并不随着锚固长度的增加而降低，且中国规范计算得到的平均黏结强度明显高于计算结果以及其他规范结果。

3.2.2 混凝土强度与锚固长度的关系

混凝土强度取C15～C70，分别计算出锚固长度然后进行比较，结果如图15(b)所示，所有结果均显示出随着混凝土强度的提高，锚固长度有减少的趋势。若以迭代计算结果为基准，规范计算得到的锚固长度均偏于安全且有一定的安全储备。

3.2.3 保护层厚度与锚固长度的关系

保护层厚度与锚固长度的关系如图15(c)所示，各规范计算公式均显示出随着保护层厚度的增加锚固长度下降的趋势，其中美国ACI 408R-03规范下降趋势最为明显，但当保护层厚度超过4D时，锚固长度不再下降。CEB-FIB规范结果显示最为保守，中国规范仅对保护层厚度超过3D时进行锚固长度的折减，因此曲线不平滑，迭代计算出来的锚固长度均远低于各国规范。

图15 锚固长度与各种参数的关系Fig.15 Relationship Between Anchorage Length and Various Parameters

3.2.4 钢筋直径与锚固长度的关系

钢筋直径与锚固长度的关系计算结果如图15(d)所示。可以看出，很明显随着钢筋直径的增加，锚固长度增加的趋势不如其他因素变化得剧烈，但大体上呈现增加的趋势，且迭代计算结果与ACI 408R-03规范趋势高度吻合，差别仅在于数值的高低，因为规范在设计公式中考虑了一定的安全系数，而迭代结果的本构来源于数据库统计，并不包含安全系数，因此迭代结果理应低于公式计算结果。中国规范在考虑黏结性能时并未考虑钢筋直径的影响，仅对直径大于25 mm的钢筋乘以1.1的安全系数，但该做法从图15(d)中可以看出是有用的，若不进行折减，则规范计算锚固长度便会低于迭代计算结果。虽然中国规范的锚固长度高于迭代计算的结果，但与其他规范相比，安全储备仍不高。

上述比较结果可以看出，数值计算得到的锚固长度均低于规范公式计算锚固长度，其中数值计算锚固长度的结果与中国规范计算结果相差最小，整体变化趋势基本相一致，且中国规范计算锚固长度最短，安全储备最低，与以往文献结论相一致[21]。推测其数值上的差别在于ACI 318-19，ACI 408R-03和CEB-FIB规范计算公式源自搭接试验数据库[22]，虽说从锚固机理上搭接试验与中心拉拔试验基本相一致[22]，但相较于中心拉拔试验，搭接试验可能会存在横向裂缝的影响，因此数值计算得到的结果低于规范公式计算结果。该算法的缺陷在于无法考虑试验构件中横向裂缝对于锚固性能的影响。

4 结 语

(1)递推迭代算法能够比较好地对构件发生锚固破坏的荷载及滑移进行预测。该算法中采用的黏结-滑移本构关系为连续函数，在计算过程中能够稳定收敛，因此可快速对锚固长度进行一个初步的合理性判断，计算成本低，在结构整体性分析中，使用该方法可以大幅简化黏结-滑移这一复杂受力关系，提高计算效率。

(2)本文采用的本构含有各种锚固参数，由于计算的高效性，可以对各种锚固参数进行分析，并且直观地观察到锚固性能与各种变量的关系，可以利用众多数据库数据本构关系进行修正，进一步完善黏结-滑移本构关系。本文针对锚固长度、混凝土强度、保护层厚度以及钢筋直径4种基本锚固进行了分析，从结果看各国规范计算锚固长度均高于迭代计算结果，具有一定安全储备，但中国规范安全储备最低，其安全储备是否足够有待通过可靠度指标进一步确认。

(3)该方法计算结果准确性很大程度上取决于黏结-滑移本构关系的正确性，除了本文中采用的本构关系所包含的变量参数外，还有部分尚未考虑的因素(钢筋位置、浇筑条件、钢筋环氧涂层、钢筋强度、特种混凝土等)。这些变量均有待进一步探究，特别是锚固长度较长的梁式试验和搭接试验中存在的横向裂缝，该方法仅考虑沿钢筋长度方向上的应力状态，而横向裂缝需要从构件整体上的混凝土应力状态进行分析，并对整体应力状态进行调整。若该算法能考虑横向裂缝并进行修正，便能运用于各类加载方式的试验，将所有的试验数据归一化并进行统计分析，目前该算法仅适用于普通钢筋及普通混凝土的锚固试验。