基于基频法的预应力混凝土箱梁疲劳刚度退化试验

周宏宇，麻全周，赵晓花，袁 慧

(1. 北京工业大学 建筑工程学院，北京 100124； 2. 中国建筑技术集团有限公司，北京 100013)

0 引 言

近年来,随着国民经济的迅速发展,桥梁上车辆运输特点发生较大变化：行车速度不断提高，交通密度不断增加，车辆荷载不断加重[1-2]。由此产生的桥梁疲劳累积损伤也更加严重。国内外学者对混凝土梁的疲劳累积损伤进行了大量研究，主要是从挠度[3-4]、应变[5-6]、刚度[7-8]、裂缝[9]等静力特性展开，研究方法较单一。此外，一些学者在疲劳刚度退化方面进行了更深入的研究，如李富民等[10]对4根预应力混凝土矩形梁进行了疲劳试验，探究了疲劳破坏、疲劳寿命退化以及弯曲刚度退化等规律。窦远明等[11-12]对 7 根预应力钢筋混凝土矩形梁进行了腐蚀、静载及疲劳试验，研究了疲劳荷载下锈蚀部分预应力混凝土梁破坏形态、疲劳寿命、刚度及跨中挠度的变化规律。

箱形截面梁因其抗弯抗扭力学性能好，被广泛应用于大跨度预应力混凝土桥梁上。相关资料显示，中国运营中的箱梁桥存在或大或小的腹板裂缝问题，甚至一些箱梁桥刚通车1年，腹板裂缝就已经非常显著。腹板裂缝直接导致了桥梁结构刚度的降低。许多学者对预应力混凝土梁的刚度退化进行了研究。胡志坚等[13]通过对 6片有黏结和无黏结预应力混凝土T形梁进行试验，分析了预应力混凝土梁的抗弯刚度退化规律，并提出了基于跨中弯矩修正系数的抗弯刚度修正公式。易伟建等[14]对无黏结预应力混凝土梁进行了静动力试验，基于梁的8阶模态值，识别了各损伤工况下的梁动刚度损伤系数，利用静力荷载-挠度关系对梁各阶静刚度损伤系数进行了研究。Das 等[15]研究发现，结构损伤开裂后其振型和频率会发生变化，且损伤过程中动刚度和静刚度变化速率不同。王凌波等[16]运用材料力学和数值模拟理论，推导出混凝土梁刚度分布推算公式，并结合影响线推算出梁的刚度实际分布状态。吴晓莉等[17]采用光纤应变测试方法获得绝对应变值，引入损伤因子定量描述混凝土梁的疲劳损伤，并提出了识别钢筋混凝土桥的疲劳累积损伤的剩余刚度法。

在桥梁动测试验中，桥梁的固有频率是最容易获取的动力特性，识别度高、容易测量，且与测量位置无关。结构频率是结构刚度和质量的函数，一般在损伤过程中结构质量不变，结构频率会随着刚度变化而变化。戴公连等[18-19]验证了运用桥梁1阶基频可以很好地反映结构刚度的变化。本文开展了基于基频法的预应力混凝土箱梁桥模型多级变幅疲劳试验，采集不同疲劳次数下箱梁基频和挠度值，采用动刚度和静刚度基本原理计算其动刚度和静刚度值，探究预应力混凝土箱梁桥在多级变幅疲劳荷载下的刚度退化规律。

1 试验梁设计

1.1 试验梁参数

依据项目背景,选取京津城际高铁线路中使用最普遍的32 m简支箱梁为试验原型梁。重点对考察的关键区段和关键截面的力学行为进行研究，依据相似理论，并综合考虑试验精度要求、模型尺寸及试验条件的可能性，采用 1∶11 的缩尺比例，制作3个缩尺模型梁构件。上顶板宽1.21 m，梁高0.275 m，下底板宽0.465 m，梁跨3 m，采用5根1×7预应力钢绞线。模型梁设计如图 1所示。

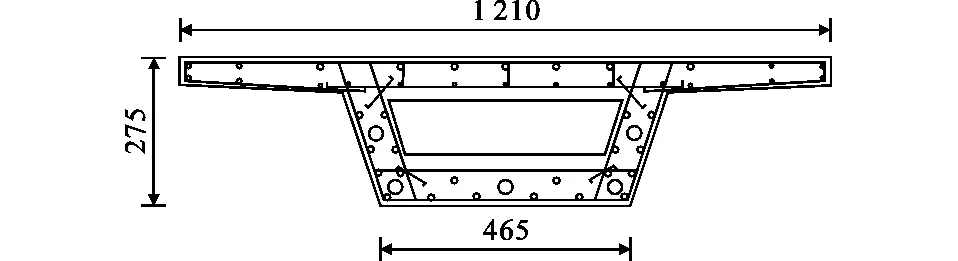
图1 模型梁设计图(单位:mm)Fig.1 Design Drawing of Model Beam (Unit:mm)

1.2 试件所用材料

混凝土中水泥、水、石、砂、外加剂的配合比为447∶170∶1 138∶640∶4.47。粗骨料选用碎石，最大粒径不大于15 mm，采用天然河砂(中砂)作为细骨料，水泥选用P.Ⅱ42.5R级硅酸盐水泥，外加剂采用铝粉和粉煤灰，掺量为4.47 kg·m-3。水为生活饮用水。

在浇筑模型梁时预留混凝土标准立方体试块和棱柱体试块，其力学性能测试与试验梁同时进行试验。依据《普通混凝土力学性能试验方法标准》(GB/T 50081—2016)，测得混凝土立方体抗压强度为51.51 MPa，轴心抗压强度为45.1 MPa，劈裂抗拉强度为4.74 MPa。 钢筋的力学性能试验按照《金属拉伸试验法》(GB 228—87)进行，钢筋力学性能实测结果如表1所示。

表1 钢筋力学性能Tab.1 Mechanical Properties of Steel Bars

2 基本原理

2.1 静刚度计算理论

简支梁跨中挠度与弯矩、轴力和扭转效应有关，但是在实际工程下轴力和扭转对挠度的贡献较小，可忽略不计。简化得到预应力混凝土等截面简支梁的刚度计算公式，由静挠度计算的刚度是梁体的整体静刚度，其计算如下

(1)

(2)

式中：B为截面抗弯刚度；E为材料的弹性模量；A为截面面积；f为结构挠度；M0，MP分别为单位荷载作用和实际荷载作用下的弯矩值；N0，NP分别为单位荷载作用和实际荷载作用下的轴力值；V0，VP分别为单位荷载和实际荷载作用下的剪力值；α为结构的挠度系数，与支撑和荷载形式等有关；G为材料的剪切模量；M为梁跨中截面的最大弯矩；L为梁的净跨；Bδ为静刚度；k为截面剪应力分布不均匀修正系数。

2.2 动刚度计算理论

结构自由振动取决于其自身的固有特性，因此结构的自由振动能反映结构本身的损伤度。结构的动荷载和动位移都与结构的固有频率有关。只要获得了固有频率就可以得出结构的刚度和内力。桥梁的第一固有频率ω1计算公式为[19-20]

(3)

式中：EI为桥梁刚度；m为梁单位长度质量。

因此，根据桥梁的固有频率，可以推算桥梁的刚度EI。固有频率所表达的是梁整体动刚度。

动刚度EIω计算公式为

(4)

3 试验加载和采集方案

3.1 疲劳加载及主要参数

本文试验在北京工业大学工程结构试验中心开展。对模型梁进行多级变幅疲劳加载和动测试验。疲劳加载采用 PMW系列500 kN电液伺服脉动疲劳试验加载装置，如图2所示。动测试验采用电磁激振器激励模型梁，以测得在不同疲劳累积次数下模型梁的基频，如图3所示。其中疲劳加载采用正弦波、集中力加载，加载频率为5 Hz。多级变幅加载参数如表2所示，其中，Pmin为疲劳荷载下限值，Pmax为疲劳荷载上限值，N为疲劳次数。由结构力学可知，简支梁的第2阶振型节点处于L/2跨附近，因此，动测试验采用电磁激振器在试验梁跨中底部进行0～1 000 Hz的扫频激振。

图2 疲劳试验加载装置Fig.2 Fatigue Test Loading Device

图3 动测试验加载装置Fig.3 Dynamic Test Loading Device

表2 多级变幅加载参数Tab.2 Multi Level Luffing Loading Parameters

3.2 数据采集及试验过程

为了采集不同疲劳次数N下预应力混凝土箱梁挠度的变化情况，在梁体底部中轴线上布置百分表，如图4所示。为了测试模型梁在不同疲劳阶段的基频，在梁体顶部中轴线上，沿跨中两侧对称布置加速度传感器，如图5所示。加速度信号用IMC模块集成式动态数据系统进行采集，如图6，7所示。

图4 模型梁百分表布置(单位:mm)Fig.4 Model Beam Dial Indicators Arrangement (Unit:mm)

图5 模型梁加速度传感器布置(单位:mm)Fig.5 Model Beam Acceleration Sensors Arrangement (Unit:mm)

图6 IMC动态数据采集软件Fig.6 IMC Dynamic Data Acquisition Software

试验由动测试验、预加载、疲劳加载、疲劳过程中停机静载疲劳试验4个部分组成。

图7 IMC模块集成式动态数据采集模块Fig.7 IMC Dynamic Data Acquisition Module

①动测试验：在安置分配梁之前对完好的模型进行1次动测，并及时对数据进行频谱分析。如果数据不好(包括异常、噪声太大等)，则重新动测。动测的有效数据为3组，分别在疲劳加载至5×104，10×104，30×104，50×104，100×104，150×104，200×104次时停机进行动测试验。动测试验时，固定加速度传感器，连接IMC动态数据采集设备，采用电磁激振器在模型梁跨中底部进行0～1 000 Hz的扫频激振，采集加速度信号数据。

②预加载：在疲劳试验开始之前需要事先进行预加载，用以检查试验装置间的接触状况，以便消除分配梁及支座等连接件之间的接触不良，并检查各相关试验仪器是否正常工作。

③疲劳加载：利用控制系统设置疲劳试验的疲劳荷载上、下限以及疲劳加载频率，然后对3根模型梁进行不同疲劳荷载上限、相同疲劳荷载下限的多级变幅加载试验，具体加载参数见表2。

④静载疲劳试验：进行疲劳加载之前先进行1次静载疲劳试验，作为疲劳0次时的加载。同时分别在疲劳加载至5×104，10×104，30×104，50×104，100×104，150×104，200×104次时停机进行静载疲劳试验。试验过程中逐级加载至疲劳荷载上限值，再进行逐级卸载，每级荷载取疲劳荷载上限值的20%。在不同疲劳次数下的静载疲劳试验中，进行疲劳静载挠度的采集和动测试验数据的采集。

4 试验现象描述

在疲劳加载过程中，所有模型梁均首先在腹板产生斜裂缝，并随着疲劳加载的进行，腹板斜裂缝沿支座向跨中45°方向延伸，裂缝宽度不断拓宽。在1/4跨到支座范围内裂缝分布较密集。模型梁典型裂缝分布如图8所示。由图8可看出，箱梁裂缝分布、裂缝走向和破坏敏感位置均与矩形梁不同，主要是因为箱梁截面较复杂，腹板属于疲劳敏感部位。腹板斜裂缝即主拉应力裂缝，主要是因为混凝土疲劳强度不满足其主拉应力的要求而造成了腹板开裂。随着疲劳幅值的增大，斜裂缝数增多，裂缝宽度较大。模型梁GF3比模型梁GF1和GF2的腹板斜裂缝密集，裂缝宽度更大。

图8 试验梁疲劳裂缝分布Fig.8 Fatigue Crack Distribution of Test Beam

5 动测试验结果分析

根据结构的动荷载和动位移计算公式，只要获得了自振频率就可以得到结构的刚度和内力。本文通过动测试验，获取桥梁的基频，来探究桥梁在不同疲劳次数下的累积损伤规律。

5.1 模型梁未开裂测得的自振频率

桥梁结构的自振频率和结构刚度是一一对应的,混凝土结构开裂前桥梁全截面参加工作,梁体各截面刚度几乎完全相同。同时，为了验证基频法评估模型梁结构使用性能的可靠性，在疲劳荷载加载前测试了模型梁的1阶自振频率，并用式(3)进行理论计算，结果对比见表3。由表3可知，3个加速度传感器的测试结果基本一致，与理论计算值误差较小。

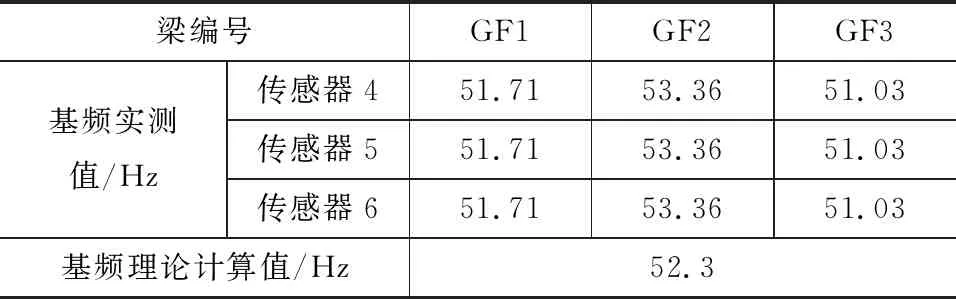
表3 模型箱梁未开裂基频测试结果Tab.3 Test Results of Basic Frequency of Model Box Girder Without Cracking

5.2 模型梁自振频率随疲劳次数的变化

结构的基频反映结构的使用性能，疲劳荷载作用下桥梁刚度的变化与基频变化是一一对应的。表4为不同疲劳次数下基频的变化。

由表4可知，随着疲劳次数的增加，模型梁的1阶频率呈现逐渐降低趋势，说明疲劳过程中模型梁刚度有所降低。其主要原因是在疲劳加载过程中，模型梁腹板裂缝不断增多、延伸、拓宽等，导致梁体不断损伤。在低幅值下的疲劳加载，模型梁GF11阶基频变化不大，说明在疲劳加载幅值较小时，桥梁满足疲劳要求。模型梁GF3是在较高幅值的疲劳加载工况，模型梁1阶频率下降较多，主要原因是腹板出现大量斜裂缝，梁体损伤较严重。在模型梁GF2和GF3中，1阶频率数据有“波动”现象，这可能是因为支座移动或弯扭耦合振动造成的。

5.3 基于基频法的预应力混凝土箱梁疲劳刚度

桥梁结构在静载下抵抗变形的能力称为桥梁的静刚度，桥梁在动荷载下抵抗变形的能力称为桥梁的动刚度。因此，静刚度一般用桥梁结构在静载下的静挠度来衡量，动刚度一般用结构的振动频率来衡量。静刚度是一个固定的值，而动刚度不是一个固定值，本文利用基频计算动刚度，用静挠度计算静刚度，并研究静刚度和动刚度的退化规律。

5.3.1 由基频反算动刚度

由式(3)可知，对于给定的桥梁，对应于某阶振型的结构自振频率只与结构的刚度EI有关。选取表4中加速度传感器5测量的数据。利用式(4)，由基频反算刚度，得到预应力箱梁在不同疲劳次数下的动刚度值，见图9。

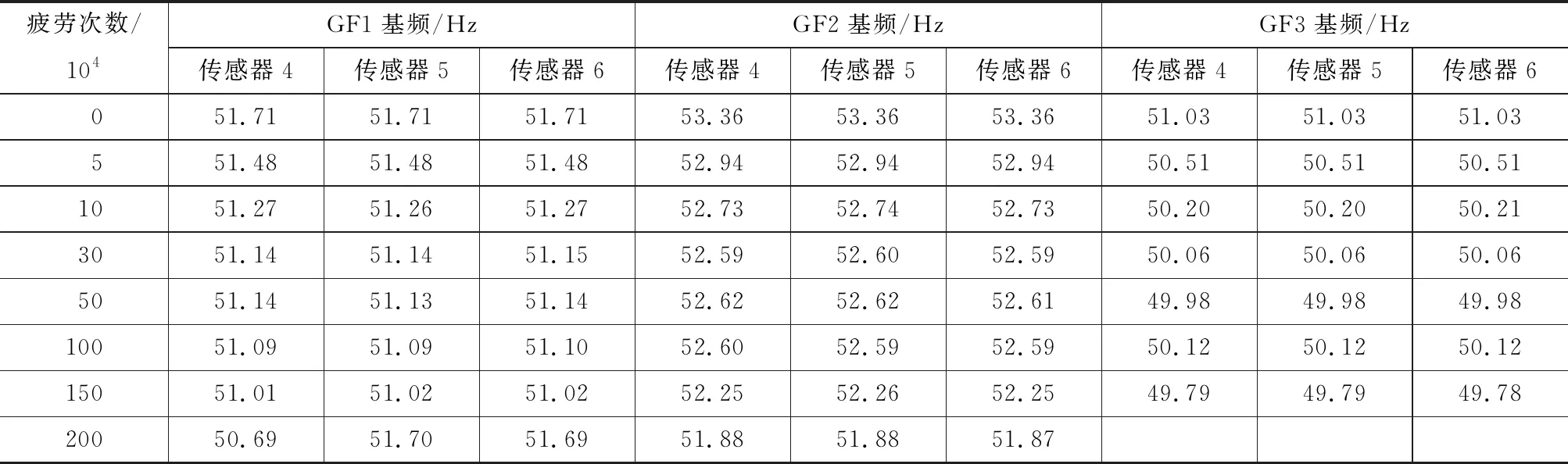
表4 不同疲劳次数下基频实测值Tab.4 Measured Values of Fundamental Frequency Under Different Fatigue Times

图9 预应力混凝土箱梁动刚度损伤变化对比Fig.9 Comparison of Dynamic Stiffness Damage Changes of Prestressed Concrete Box Girders

预应力混凝土箱梁疲劳荷载水平不高时，模型梁均未发生钢筋疲劳断裂(图9)，预应力混凝土箱梁疲劳刚度的退化类似于混凝土疲劳损伤发展3个阶段的前2个阶段：刚度退化快速期、刚度退化稳定期[21-22]。箱梁构件刚度退化分阶段的主要原因是混凝土在截面刚度上占主导地位，同一截面上不同高度的混凝土应力状态不同，混凝土损伤程度也不同，从而导致刚度退化出现了2阶段过程，并且可以推断在箱梁临近疲劳破坏时，也会出现类似于混凝土疲劳损伤的第3阶段：快速退化阶段。由图9结合试验过程可以看出，在疲劳初期，试验梁刚度有较大幅度的下降，退化率占整个退化过程的40%～60%。疲劳初期占整个加载时期的10%～15%。在疲劳中期，试验梁疲劳刚度与疲劳次数呈线性关系，此阶段为刚度退化稳定期，约占整个加载周期的80%。疲劳中期，模型梁刚度退化率占整个退化过程的10%～40%。

对比3根试验梁刚度退化曲线可以得出，疲劳上限值越大，刚度退化越明显。在疲劳前期，GF3梁表现出较大的刚度退化速率，刚度退化率达到58%；疲劳荷载上限值较小的GF1梁刚度退化率约为40%。

5.3.2 由挠度反算静刚度

由简化的预应力混凝土简支梁的刚度计算式(2)，并根据本文试验的加载方案及箱梁结构加载形式，α取为23/216，得到挠度fn对应的静刚度Bδn

(5)

式中：P为挠度fn对应的荷载。

可根据式(5)，由不同疲劳次数下模型梁的静挠度计算出疲劳静刚度值。疲劳静挠度取静载疲劳试验中不同疲劳阶段的疲劳荷载上限值作用下的试验挠度值。由式(5)计算得到的疲劳静刚度值如图10所示。随着疲劳次数的增加，模型梁静刚度值不断下降，呈现先快速、后平稳2阶段变化规律。在疲劳初期，模型梁静刚度迅速退化；模型梁刚度退化率占其整个退化过程的60%～70%。3根箱梁的疲劳静刚度退化曲线趋势相似。在疲劳中期，箱梁疲劳静刚度呈线性退化规律，故也称为静刚度稳定退化期，其约占整个加载周期的60%。对比3根箱梁构件的静刚度退化幅度发现，疲劳荷载上限值越大，静刚度退化幅值越大；GF1，GF2，GF3梁200×104次疲劳加载期间，疲劳静刚度退化幅值分别为5.14×107，5.19×107，5.84×107N·m2。分析其原因可能是因为疲劳荷载上限值越大，梁体开裂就越严重，大量的裂缝会增大梁体的下挠，从而导致梁体静刚度减小。

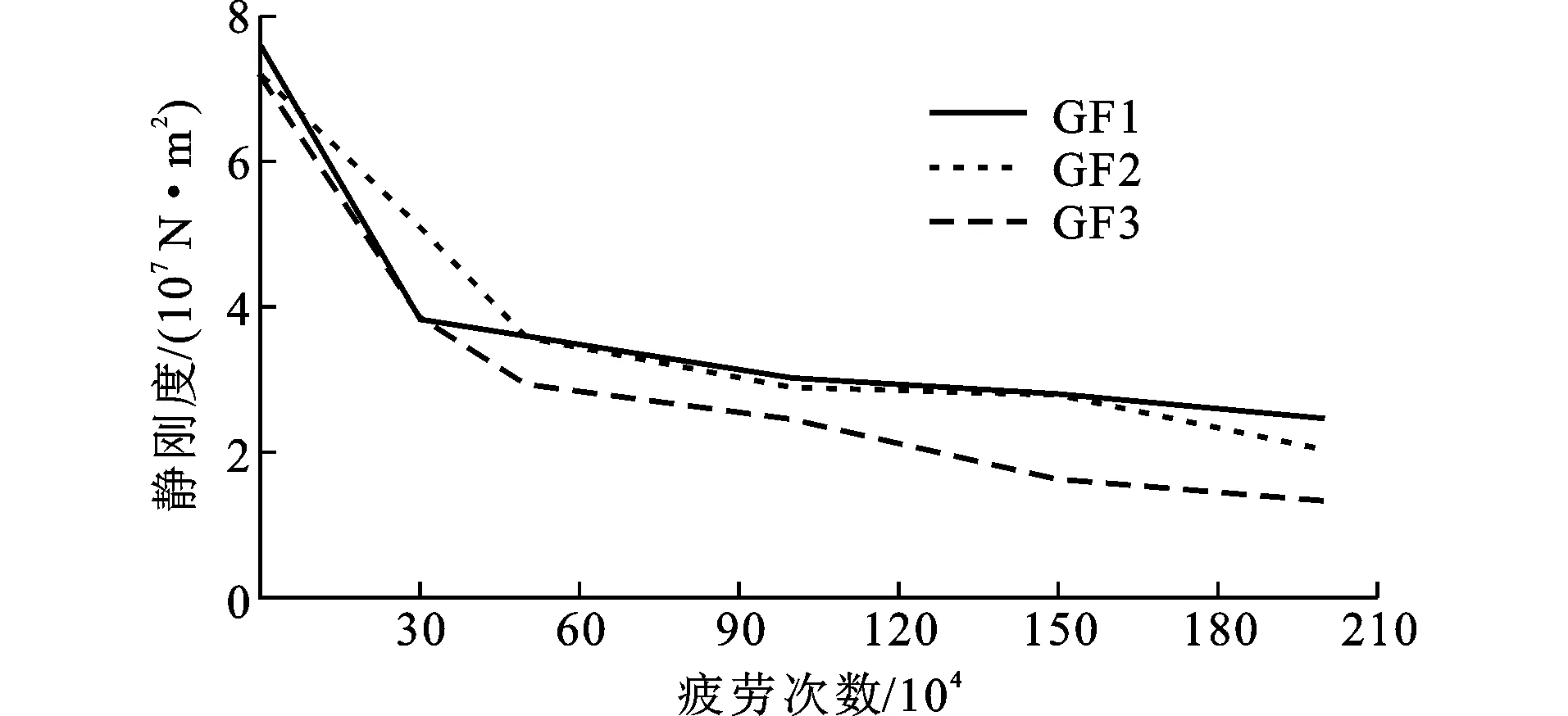
图10 预应力混凝土箱梁动刚度损伤变化对比Fig.10 Comparisons of Dynamic Stiffness Damage Changes of Prestressed Concrete Box Girders

对比梁体的疲劳静刚度和动刚度发现，二者退化规律相似：呈现先快速、后平稳2阶段规律。这符合卫军等[20-22]进行的疲劳刚度退化3阶段过程的前2个阶段。

6 结 语

(1)基于多级变幅疲劳试验，对预应力混凝土箱梁进行了疲劳加载，发现箱梁构件疲劳裂缝分布、裂缝走向和破坏敏感位置与矩形梁不同。各模型梁在疲劳过程中，均首先在腹板产生斜裂缝，腹板斜裂缝主要分布在从支座到1/4跨范围内，不断向顶板和底板斜向延伸。腹板疲劳斜裂缝产生的主要原因是腹板混凝土斜截面承载能力不足。因此，疲劳荷载会降低混凝土斜截面的承载力，有使延性破坏变成脆性破坏的危险。

(2)预应力混凝土箱梁的疲劳动刚度和静刚度退化规律相似，均呈现先快速、后平稳2阶段规律。在疲劳初期，模型梁动刚度退化率占整个退化过程的40%～60%；模型梁静刚度退化率占整个退化过程的60%～70%。在疲劳中期，模型梁疲劳动刚度和静刚度呈线性退化，此阶段也称刚度退化稳定期。模型梁疲劳动刚度退化稳定期约占整个加载周期的80%；模型梁疲劳静刚度退化稳定期约占整个加载周期的60%。

(3)疲劳荷载上限值越大，动刚度退化越明显，静刚度退化幅值越大。分析其原因可能是疲劳荷载上限值越大，梁体开裂就越严重，大量的裂缝会增大梁体的下挠，从而导致梁体静刚度减小。