梯形波折钢板剪力墙内嵌墙板抗侧性能研究

窦 超，朱仰泽，解 程，谢志栋，杨 娜

梯形波折钢板剪力墙内嵌墙板抗侧性能研究

窦 超，朱仰泽，解 程，谢志栋，杨 娜

(北京交通大学土木建筑工程学院，北京 100044)

与普通平钢板剪力墙相比，波折钢板剪力墙的抗侧性能与设计方法仍有待研究．利用有限元方法分析波折钢板剪力墙体系中内嵌墙板的抗侧性能和承载机制，提出设计建议．首先，通过对比梯形波折钢板及与之对应的正弦波折钢板的抗侧性能，证明梯形波折优于正弦波折，且子板面倾斜角度越大，抗侧承载力越大；设计正交有限元试验研究波折参数(宽高比/、高厚比/、波折数量/l、波折角度)对内嵌钢板极限和残余承载力的影响，指出宽高比和波折角度对墙板抗侧性能的影响最大．其次，通过比较波折钢板墙与对应平钢板墙的边缘框架内力分布，揭示了内嵌波折钢板的两种抗侧力机制，设计合理的波折钢板能够实现面内剪切屈服的抗侧机制，满足稳定的屈曲后强度的要求；而屈曲后强度下降的墙板，将对边缘柱产生较大的附加弯矩，削弱结构整体性能．对于大宽高比的钢板墙来说，竖直放置的波折钢板面外变形更小，剪切屈服能够充分发展，具有更优越的性能．最后，对工程常用参数范围的波折钢板进行抗侧承载力分析，给出极限承载力的拟合公式，提出保持屈曲后承载力稳定的设计建议．研究发现，减小内嵌墙板的正则化高厚比可以提高其延性．根据提出的设计建议设计的墙板可以实现面内剪切屈服的抗侧承载机制．

波折钢板剪力墙；抗侧机制；抗侧承载力；屈曲后性能；设计建议

平钢板剪力墙(FSSWs)体系具有良好的抗侧力性能，一直以来被广泛应用于高层结构中．1973年日本学者Takahashi等[1]对非加劲薄钢板墙及加劲钢板墙进行了拟静力试验，随后大量研究工作在国内外相继展开[2-5]．理论研究及工程实例表明，钢板剪力墙结构是一种优越的延性耗能双重抗侧力体系．经过四十余年的发展，平钢板剪力墙、加劲钢板墙的计算理论及设计方法趋于完善．但内嵌薄平钢板墙仍存在以下问题：①在风荷载或小震作用下易屈曲变形或振动而影响舒适度，运输安装过程中的变形也不易控制；②往复荷载作用下，滞回曲线存在明显的捏缩现象，降低了其耗能能力；③屈曲后薄钢板墙的拉力带锚固于框架梁柱，对边缘框架带来较大负担，产生的附加弯矩将导致框架柱过早破坏．

相比传统平钢板剪力墙，波折钢板剪力墙(SCSWs)具有更优越的性能．波折的存在大大增强了面外刚度，使其综合了厚钢板墙和加劲钢板墙的优势，不会过早屈曲，设计合理时呈现受剪屈服的抗侧机制，对边缘框架的锚固刚度要求以及附加弯矩的不利影响大幅降低，滞回曲线更为饱满[6-12]．

国内外学者针对波折钢板墙在单向推覆和循环荷载下的结构性能进行了研究．Farzampour等[13-14]提出了一种基于拉力带抗侧力机制的名为“CPFI”的设计方法．Shon等[15]进行了波折钢板墙的循环荷载试验，结果证明波折钢板墙的耗能能力优于平钢板墙．Vigh等[16]发现，在某些波折参数设计不合理的情况下，波折钢板墙表现出较差的延性．Zhao等[17]对波折钢板墙和平钢板墙进行了数值模拟，指出与薄平钢板墙的拉力带抗侧机制[18]不同，深波纹钢板墙依靠钢板剪切屈服抵抗侧力．Tong等[19-20]研究了竖向加劲波折钢板剪力墙的抗侧承载力．Dou等[21-22]研究了正弦波折钢板墙在单向荷载下的抗侧承载力和屈曲后性能，提出了预测荷载-位移曲线的拟合公式．Hosseinzadeh等[23]进行了两种不同波折角的梯形波折钢板墙试验．Cao等[24]研究了一个双层单跨波折钢板墙的滞回性能，并且提出了其在侧向荷载作用下的板框相互作用模型．

然而，前述研究大都局限于通过变参数对比分析得到波折钢板墙性能影响规律的定性结论，其相关设计方法尚不明确，设计人员在初步设计时墙板的具体参数选取仍无章可循．此外，本课题组已有研究[22, 25-26]发现，尽管波折钢板墙有较高的极限承载力，但在特定参数范围内存在屈曲后强度大幅下降的情况．目前大多数研究仅给出内嵌墙板最大极限抗侧承载力的设计公式，而忽视了其屈曲或屈服后承载性能及延性．

针对上述问题，笔者基于有限元数值分析，对单向推覆受力下的内嵌波折墙板的抗侧性能进行研究，揭示关键参数对墙板抗侧机制以及屈曲或屈服后承载力和延性性能的影响；通过引入墙板抗剪的正则化高厚比，提出墙板极限承载力的计算公式和保证残余承载力稳定的几何参数的优化取值建议，供设计人员采用．

1 有限元模型及验证

如图1所示，分析中采用单层单跨框架，内嵌水平放置的梯形波折钢板．边缘框架为刚性，钢板与框架之间四边刚接，梁柱铰接以保证内嵌墙板单独承担剪力．不考虑体系的竖向荷载，其影响在后续研究中讨论．

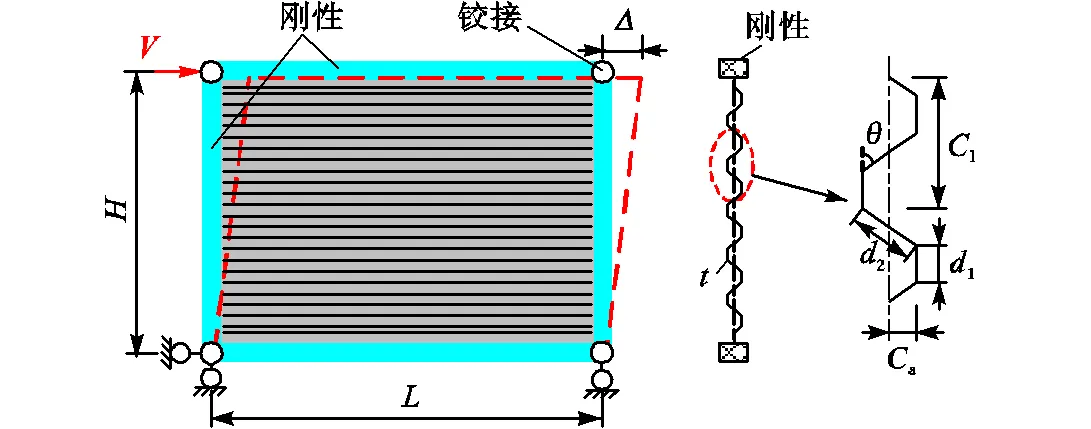
图1 波折钢板剪力墙分析模型

采用软件ANSYS13.0[27]建立有限元模型，所有构件均采用SHELL181壳单元进行模拟．通过耦合梁柱连接处节点位移的方式实现铰接，设置边缘梁柱弹性模量为100(为钢材弹性模量)来模拟其刚性．为了保证计算精度，根据文献[22]的建议，每个波折子板面(图1中1和2边)至少划分5个壳单元，并保证每个壳单元的长宽比小于1.5．波折钢板选用双折线等向强化本构和von Mises屈服准则，弹性模量＝206GPa，泊松比＝0.3．需要指出的是，在之前的研究[22]中发现，材料的强化对推覆荷载下的屈曲后强度有显著影响．所以，本文采用双折线材料模型，屈服强度y＝235MPa，切线模量t＝0.01．以1阶弹性屈曲模态/750倍的归一化位移值作为初始缺陷，与参考文献[17，22]一致．

加载方式为顶梁处位移加载，最大层间位移角/＝2.0%[28]．约束边缘梁的面外位移．如图1所示，分析中涉及5个独立参数，分别是宽高比/、高厚比/、波折数量/l、波形比a/l和波折角度．其中、、、l、a分别代表钢板的宽度、高度、厚度、波长与波高．

为了验证有限元方法的有效性与准确性，将有限元与试验结果对比．选取Qiu等[7]文章中的试件HCoPSW-Ⅰ进行模拟，材料本构与试验得到的应力应变曲线一致，选用随动强化模型，推覆和循环加载的结果与试验结果见图2．有限元计算值与试验值拟合良好，证明可以用ANSYS进行波折钢板墙的分析.

图2 有限元与试验结果对比

2 波折钢板几何参数的影响

之前的研究表明波折钢板墙中的内嵌钢板有较高的初始侧向刚度和极限承载力[17]．但在某些情况下，其延性可能较差[7,20,22]，在荷载-位移曲线中表现为承载力达到峰值后出现明显下降．

考虑如下两个典型算例：

(1)＝3.2m，＝2.0，l＝0.40m，a＝0.20l，＝8mm，＝90°；

(2)＝3.0m，＝1.0，l＝0.30m，a＝0.10l，＝6mm，＝45°．

如图3所示，典型的荷载-位移曲线包括上升部分和屈曲后部分．定义达到最大抗侧承载力s或侧向刚度突然改变时为“极限状态”，达到最大层间位移时为“残余状态”，对应的承载力为残余承载力r；y＝y是波折板的剪切屈服荷载，y是钢材剪切屈服应力．

本文中，“稳定的屈曲后强度”或“良好的延性”表示达到最大层间位移角2.0%之后，r仍大于85%s．相反地，“屈曲后强度不足”或“延性不足”表示残余承载力r远小于85%s．对于算例1，残余承载力系数r0.97s，而算例2的残余承载力系数r0.67s．这表明，必须适当选择波折钢板的参数以避免屈曲后承载力出现大幅度下降．

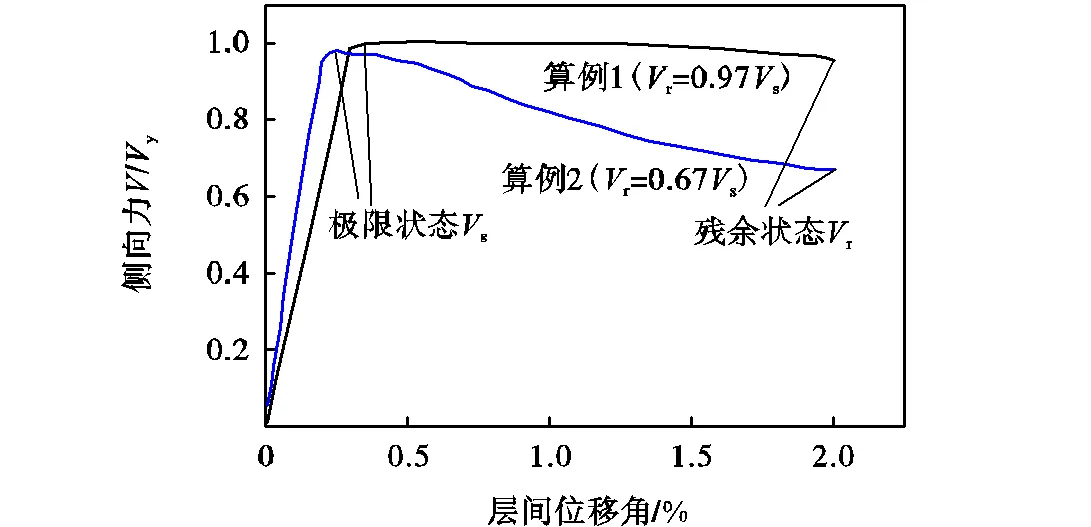
图3 典型波折钢板的荷载-位移曲线

2.1 子板面波折角度的影响

改变两个典型算例中波折钢板子板面的波折角度，并与对应的正弦波折钢板对比，图4给出了其抗侧承载力的计算结果．

可以看出，对于给定的波折钢板，极限和残余承载力随着子板面倾斜角度的增大而增大．波折钢板可以视作是正交异性板，增加其波折角度，垂直于波折方向的弯曲刚度x随之增加，进而减小面外变形，增强侧向承载力．此外，相比正弦波折钢板墙，一般的梯形波折钢板墙拥有更好的抗侧性能．因此，在设计梯形波折钢板墙时，应当选用更大的波折角度，以实现更优的抗侧性能．

2.2 正交有限元试验

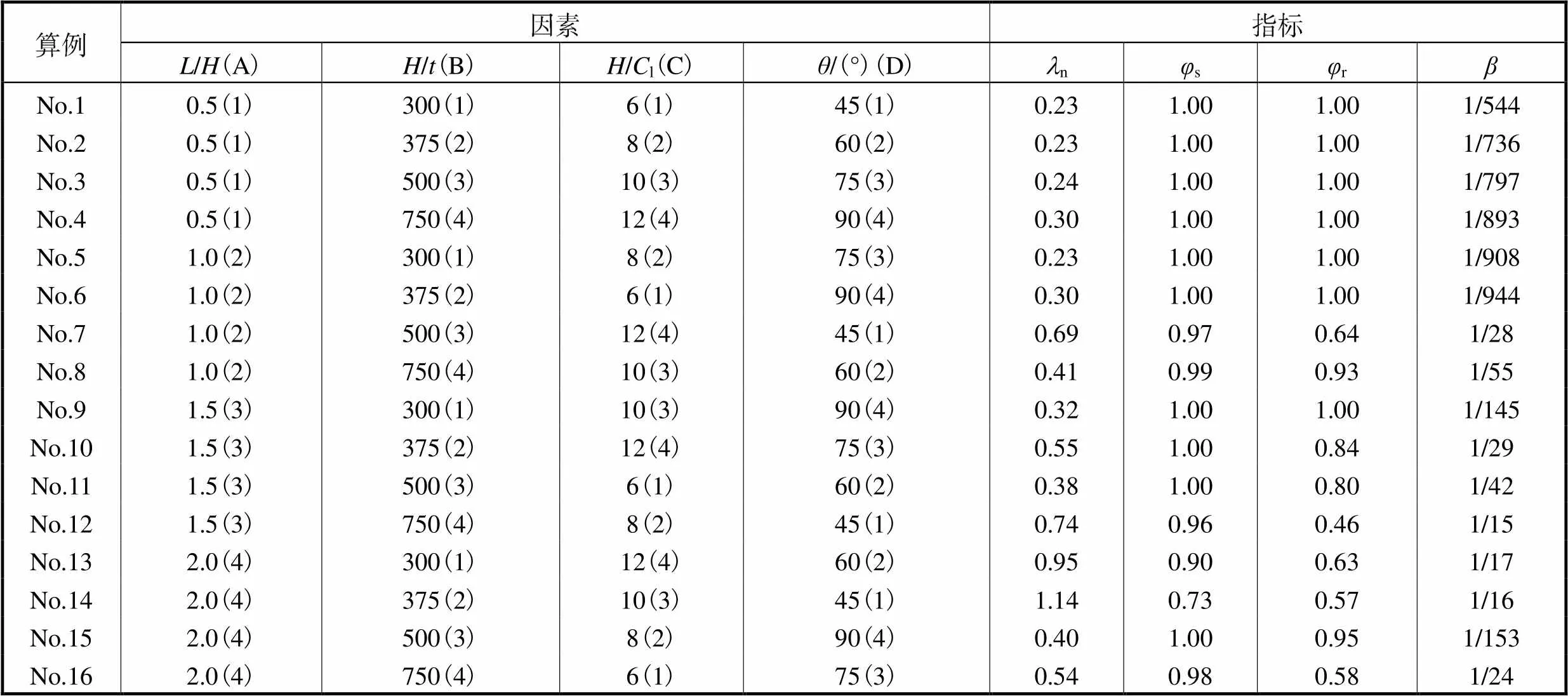
为了研究波折钢板几何参数对抗侧性能的影响，进行正交有限元分析．板面整体高度3.0m，每一个子板面的宽度均相同(1＝2)，因此/、/、/l和决定了钢板特性．基于正交试验阵列，对每一个因素(///l、分别记作A、B、C、D)选择4个水平，如表1所示．

图4 子板面倾斜角度对抗侧承载力的影响

表1 波折钢板的几何参数及水平

Tab.1 Factors and levels of steel corrugated shear walls

选择4个指标来评价以上参数对墙板抗侧性能的影响，分别是极限承载力系数s、残余承载力系数r、内嵌板正则化高厚比n以及最大面外变形系数，计算公式为

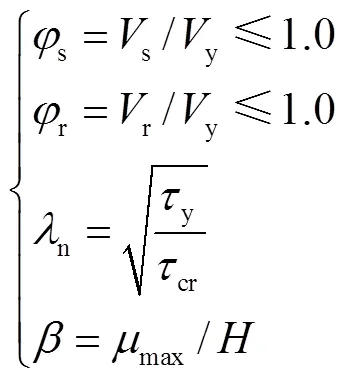
式中：cr为波折板弹性屈曲应力；max为最大面外 位移．

推覆分析的结果如表2所示．

表2 正交有限元试验结果

Tab.2 Orthogonal test results

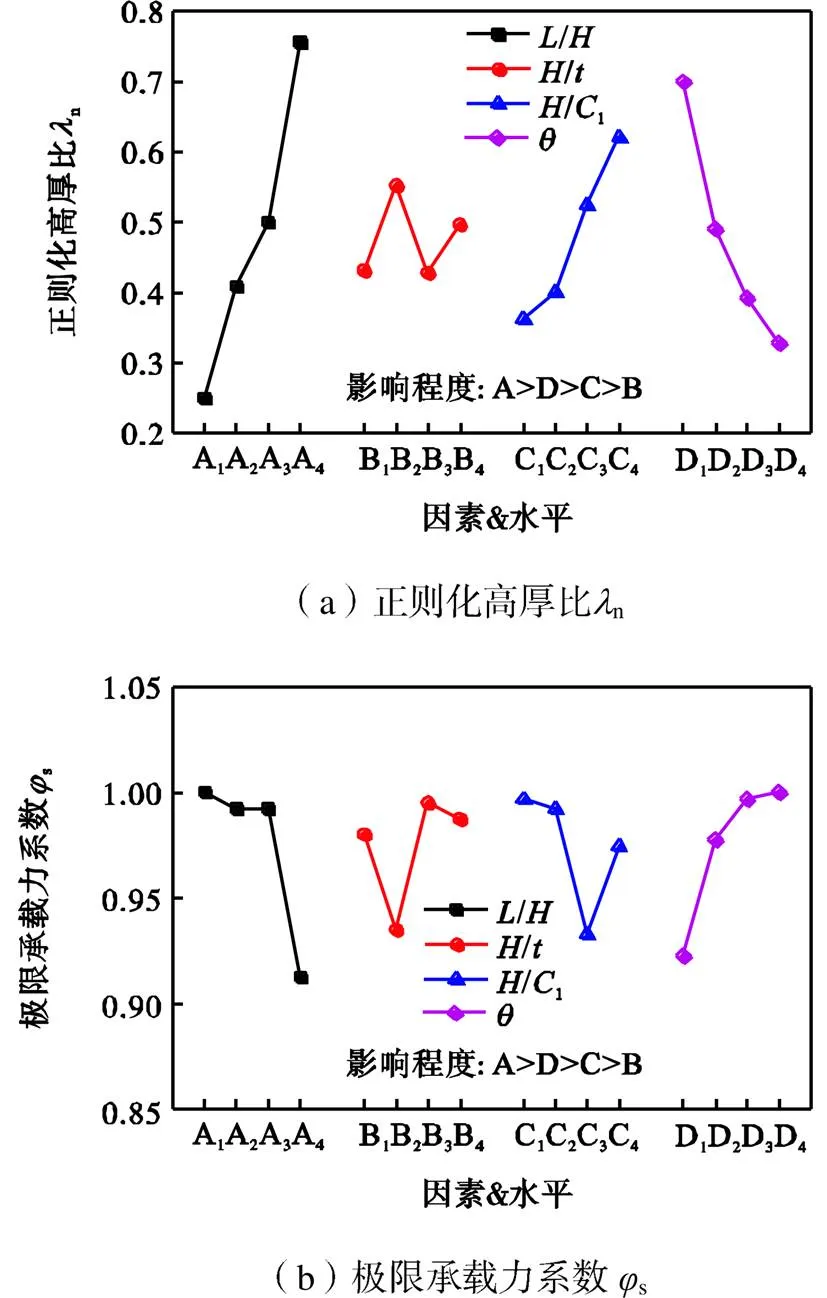
在正交有限元试验中，指标的平均值变化能够反映各影响因素的重要性，结果绘于图5．可以看出：①增大波折角度或减小宽高比/、波折数量/l能够显著降低正则化高厚比n，即波折板刚度增大，性能得到提升；②除大宽高比(/2.0)的情况外，极限承载力系数均接近1.0；③减小宽高比、增大板厚或波折角度可以提高残余承载力；④在这4个参数中，宽高比和波折角度对所有指标的影响最大．降低宽高比、增大波折角度可以提高波折板的刚度，有助于降低面外变形，增强其屈曲后强度．

基于以上正交有限元分析，提出以下建议：①对于梯形波折钢板推荐采用大波折角度(≥60°)，波形比a/l尽量大于等于0.10；②对宽高比较大(/≥1.5)的试件，应选择适当的板厚以避免屈曲后强度不足的情况，/应不小于1/500(对于表2中的算例，≥6mm)．

分析表2中的两个算例(No.5和No.7)．将推覆作用下的荷载-位移曲线绘于图6．算例No.7正则化高厚比n＝0.69，No.5的板面波折角度和板厚更大，正则化高厚比n＝0.23．算例No.5在推覆过程中表现出稳定的抗侧承载力．与之相反，No.7的抗侧承载力自峰值点后下降了约34%．图7分别给出了两个算例在极限和残余状态下的应力和变形情况，其中应力图中的灰色区域代表应力超过了屈服强度．对于算例No.5，残余状态(/＝2.0%)下墙板几乎所有区域进入塑性，同时有r＞s，即残余承载力大于极限承载力．从面外变形方面来看，算例No.5的面外位移约为/908，远小于No.7的/28．

因此，可以通过增大面外刚度的方式来减小波折板的面外变形，进而提高其抗侧性能．如Tong等[20]在研究中提到的通过增加竖向加劲肋的方式能够有效提高波折钢板的抗侧性能．

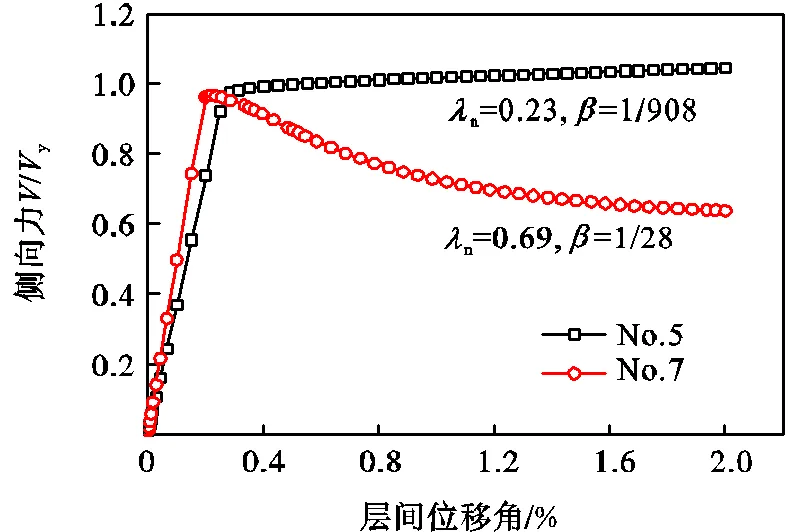
图6 两种典型算例的荷载-位移曲线

图7 残余状态下的von Mises应力和面外变形

3 波折钢板在剪切作用下的抗侧机制

为了探究波折钢板剪力墙的抗侧力机制和板框相互作用，下面分析在推覆荷载作用下极限和残余状态的框架内力．

选择算例No.5和No.7及与之相对应的平钢板墙(、、均相等)进行比较，将有限元分析得到的框架的内力分布绘于图8和图9．max和max代表对应的平钢板墙在推覆过程中的最大框架内力．可以看出：①算例No.5的极限承载力更高、屈曲后强度更稳定，与平钢板墙相比，框架弯矩非常小．这说明与平钢板墙的拉力带抗侧机制不同，其利用板内剪切屈服来抵抗侧力；②算例No.7在极限状态下柱子的弯矩(0.23max)小于对应平钢板墙的柱子弯矩(0.80max)，但不可忽略．随着层间位移的增大，柱子最大弯矩显著增大，残余状态时达到1.1max，超过了对应平钢板墙的柱子弯矩(1.0max)．这说明内嵌板的变形会导致柱子产生附加面内弯矩；③算例No.7中梁的附加弯矩非常小，这是因为波折板是水平放置的，竖向的压缩刚度很小，拉力无法传递到梁上；④观察轴力分布，可以看到左柱受拉而右柱受压．与平钢板墙相比，左柱的轴力峰值更大而右柱更小，在施加从上层结构传来的压力之后，能够抵消左柱的拉力，对结构是有利的．

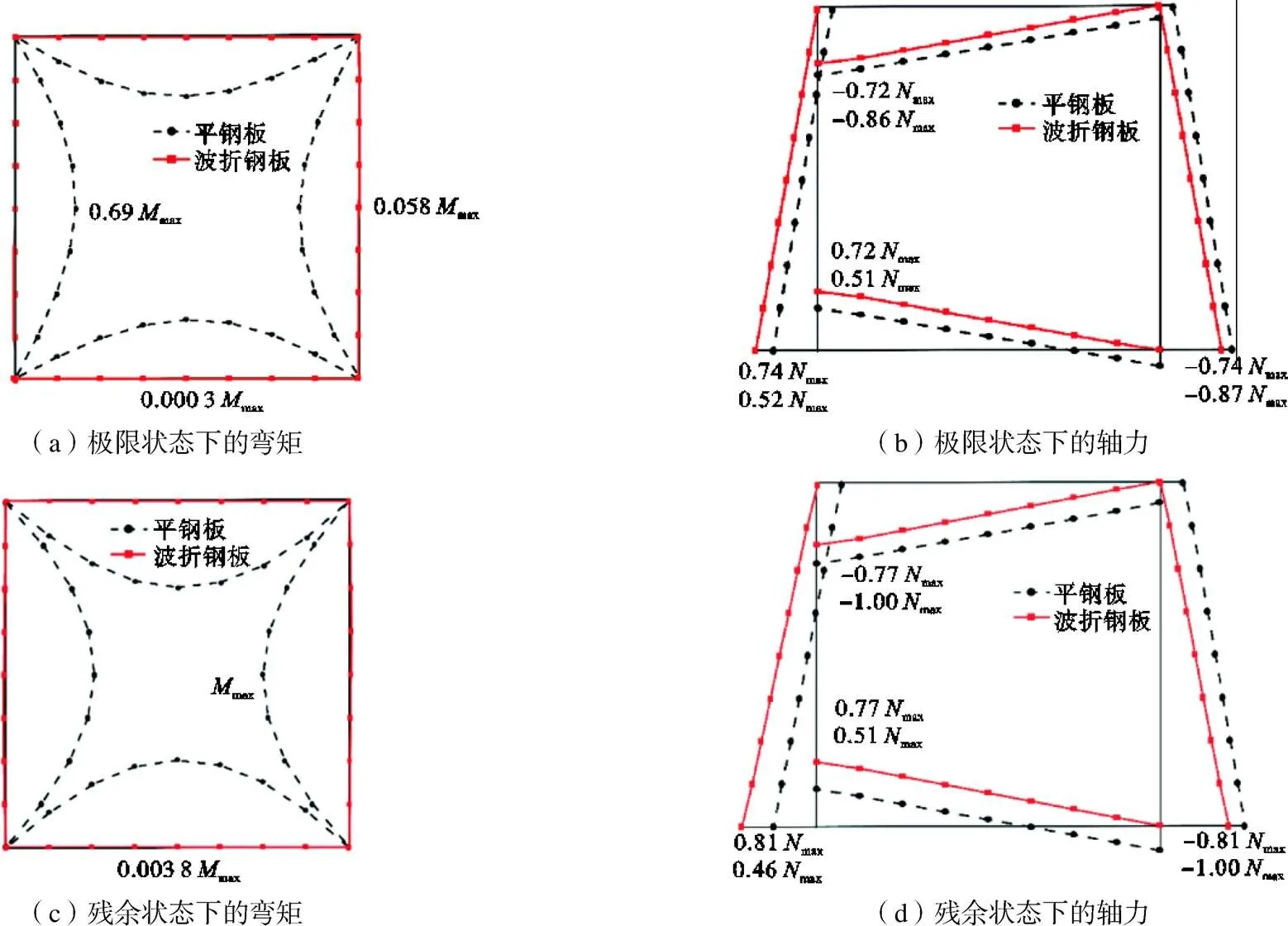
图8 算例No.5的框架内力

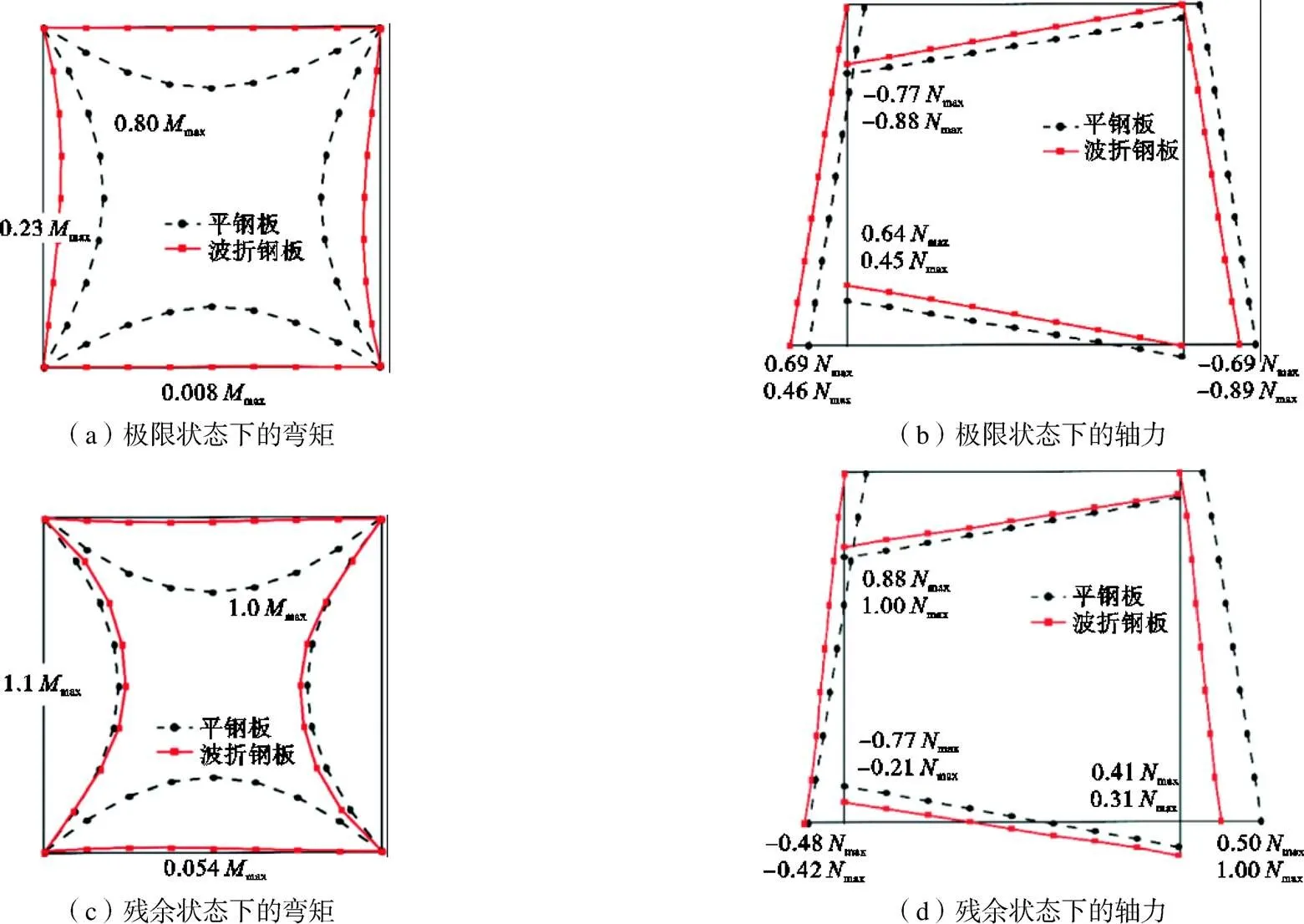
图9 算例No.7的框架内力

总地来说，设计合理的波折钢板墙有较高且稳定的抗侧承载力，通过板内剪切屈服来抵抗侧向力，这也使得边缘框架的附加弯矩很小．相反地，对于屈曲后强度不足的钢板，边缘框架产生很大的附加弯矩，会削弱结构整体性能．

波折钢板剪力墙中的内嵌墙板既可以水平放置也可以竖直放置[7]，放置方式不同导致性能也有差异．下面分析表2中的16个算例在内嵌板竖直放置时的抗侧性能．图10给出了内嵌板竖直与水平放置时的残余承载力的对比．

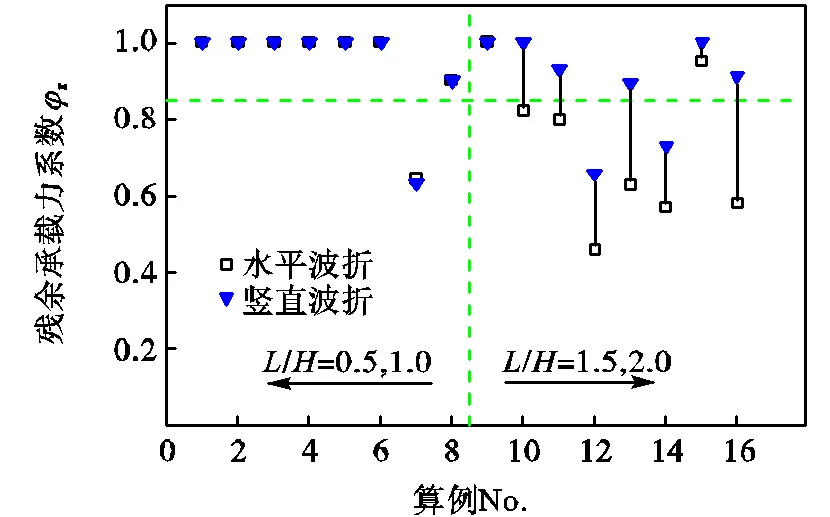
图10 波折板不同放置方式残余承载力的对比

可以看出，当/≤1.0时，波折方向对屈曲后性能影响很小．而当/≥1.5时，波折板竖直放置能显著增强其残余承载力，此时大多数算例的残余承载力系数r≥0.85．

以算例No.13为例，对波折板水平和竖直放置两种情况进行分析，将其在残余状态下的变形和应力分布绘于图11．结果表明，波折竖直放置时的面外变形小于水平放置时，这使得钢板剪切屈服能充分发展，从而有更高的残余承载力．因此，大宽高比的钢板墙的内嵌波折钢板可以选择波纹竖直放置．

图11 波折板不同放置方式的变形与内力对比

4 波折钢板的抗侧承载力分析

4.1 极限承载力

为了提出极限与残余承载力设计公式，进一步进行有限元计算．算例参数取＝3.0m，＝6～12mm，a/l＝0.10～0.25，/＝0.5～2.0，/l＝6～12，＝45°～90°，基本涵盖工程常用的参数范围．极限承载力系数s随正则化高厚比n的变化趋势如图12所示．

从图中可以看出，除宽高比＝2.0的情况外，波折板的极限承载力都接近全板屈服时的剪力．结果表明，极限承载力随正则化高厚比连续分布，给出拟合公式为

4.2 残余承载力

残余承载力系数随正则化高厚比的变化趋势如图13所示．然而，与极限承载力系数不同，其分布较为离散，很难获得统一的拟合公式．可以看出当/＝0.5时，大多数算例的r不小于0.95；当/＝1.5或2.0时，大多数算例的r小于0.85，即屈曲后强度出现明显下降．

图13 残余承载力系数

实际工程中应用波折钢板墙时，其内嵌板应该具有较高的极限承载力和稳定的屈曲后强度．在图14中重新绘制残余承载力的结果，当n≤0.35(1区)时，残余承载力系数大多大于0.90，这时内嵌墙板表现出板内剪切屈服的性质．对于0.35＜n＜0.60的部分，经过合理的设计，也有可能实现r≥0.85s，保持良好的延性性能(2区)．

在大量数值分析结果的基础上，表3给出了波折钢板几何参数的建议取值范围，可供初步设计时选用．在此范围内的波折墙板大部分均处于图14中的“1区”和“2区”，表现为以剪切屈服机制为主，极限承载力s接近剪切屈服强度，同时残余承载力s＞0.85r，意味着墙板到达最大层间位移角时仍具有良好的延性．

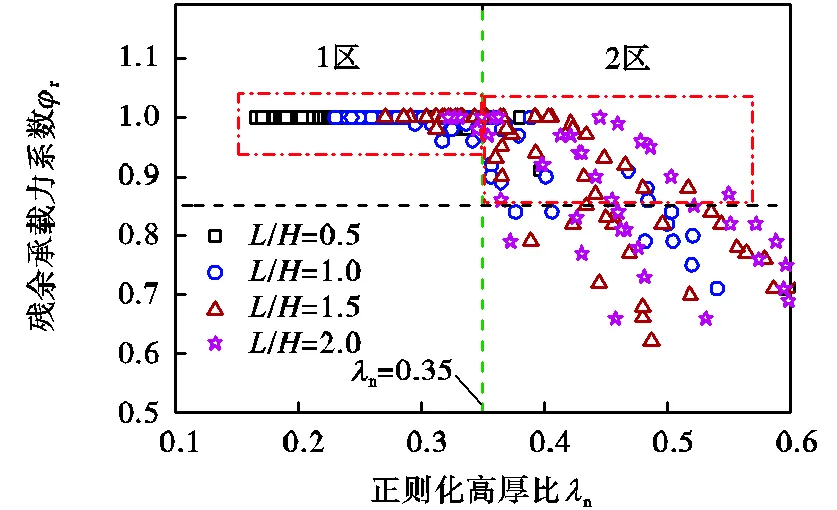
图14 波折钢板的设计准则

表3 波折钢板参数的设计建议

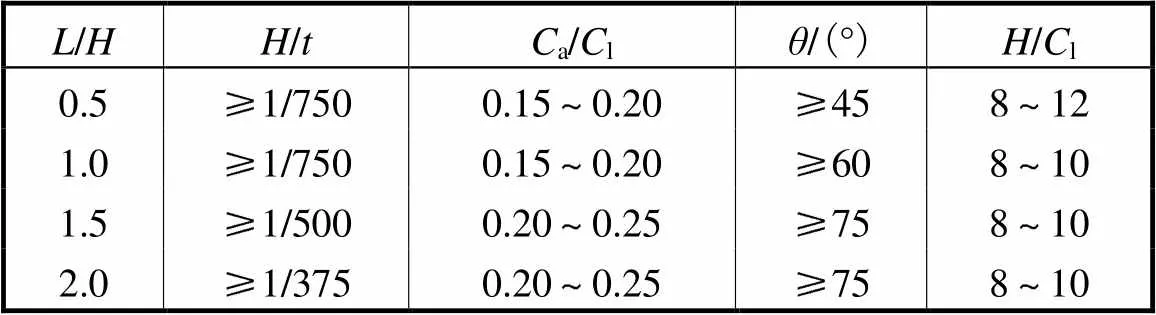
Tab.3 Parameter recommendations for corrugated pan-els

5 结 论

笔者主要研究了波折钢板剪力墙中内嵌钢板的抗侧承载力与承载机制，提出了钢板参数的设计建议，以满足极限承载力与屈曲后强度的要求．主要结论如下．

(1) 梯形波折钢板的抗侧承载力优于正弦波折钢板．在设计中推荐使用子板面倾斜角度更大的梯形波折刚板，以保证稳定的屈曲后强度．

(2) 波折方向对抗侧承载力的影响与宽高比有关，当/≥1.5时，波折板竖直放置能显著增强其残余承载力．

(3) 大多数梯形波折钢板能够实现全板剪切屈服，达到较高的极限承载力．文中给出的拟合公式可以用来预估构件的极限承载力．

(4) 按照设计准则设计的钢板墙能够实现足够的面外刚度、较高的极限承载力、稳定的屈曲后强度和良好的延性，在侧向力作用下，其表现出面内剪切屈服受力特征，对边缘框架产生的附加弯矩很小．

［1］ Takahashi Y，Takemoto Y，Takeda T，et al. Experimental study on thin steel shear walls and particular bracings under alternative horizontal load：Preliminary report[C]// IABSE Symposium on Resistance and Ultimate Deformability of Structures Acted on by Well-Defined Repeated Loads. Lisbon，Portugal，1973，260(10)：185-191.

［2］ Thorburn L J，Kulak G L，Montgomery C J. Analysis of Steel Plate Shear Walls[R]. Edmonton：Department of Civil Engineering，University of Alberta，1983.

［3］ Sabelli R，Bruneau M. AISC Design Guide 20—Steel Plate Shear Walls[R]. Chicago：American Institute of Steel Construction，2006.

［4］ 聂建国，樊健生，黄 远，等. 钢板剪力墙的试验研究[J]. 建筑结构学报，2010，31(9)：1-8.

Nie Jianguo，Fan Jiansheng，Huang Yuan，et al. Experimental research on steel plate shear wall[J]. Journal of Building Structures，2010，31(9)：1-8(in Chinese).

［5］ 郭彦林，周 明. 钢板剪力墙的分类及性能[J]. 建筑科学与工程学报，2009，26(3)：1-13.

Guo Yanlin，Zhou Ming. Categorization and performance of steel plate shear wall[J]. Journal of Architecture and Civil Engineering. 2009，26(3)：1-13(in Chinese).

［6］ Emami F，Mofid M，Vafai A. Experimental study on cyclic behaviour of trapezoidal corrugated steel shear walls[J]. Engineering Structures，2013，48：750-762.

［7］ Qiu Jing，Zhao Qiuhong，Yu Cheng，et al. Experimental studies on cyclic behaviour of corrugated steel plate shear walls[J]. Journal of Structural Engineering，2018，144(11)：04018200-1-04018200-12.

［8］ Kalali H，Hajsadeghi M，Zirakian T，et al. Hysteretic performance of SPSWs with trapezoidal horizontal corrugated web-plates[J]. Steel and Composite Structures，2015，19(2)：277-292.

［9］ Elgaaly M，Caccese V，Du C. Postbuckling behavior of steel-plate shear walls under cyclic loads[J]. Journal of Structure Engineering，1993，119(2)：588-605.

［10］ Roberts T M. Seismic resistance of steel plate shear walls[J]. Engineering Structure，1992，17(5)：344-351.

［11］ 王 威，张龙旭，苏三庆，等. 波形钢板剪力墙抗震性能试验研究[J]. 建筑结构学报，2018，39(5)：40-48.

Wang Wei，Zhang Longxu，Su Sanqing，et al. Experimental research on seismic behaviour of corrugated steel plate shear wall[J]. Journal of Building Structures，2018，39(5)：40-48(in Chinese).

［12］ Edalati S A，Yadollahi Y，Pakar I，et al. Numerical study on the performance of corrugated steel shear walls[J]. Wind＆Structures，2014，19(4)：405-420.

［13］ Farzampour A，Mansouri I，Lee C H，et al. Analysis and design recommendations for corrugated steel plate shear walls with a reduced beam section[J]. Thin Walled Structures，2018，132：658-666.

［14］ Farzampour A，Laman J A，Mofid M. Behavior prediction of corrugated steel plate shear walls with openings[J]. Journal of Constructional Steel Research，2015，114：258-268.

［15］ Shon S，Yoo M，Lee S. An experimental study on the shear hysteresis and energy dissipation of the steel frame with a trapezoidal-corrugated steel plate[J]. Materials，2017，261：1-19.

［16］ Vigh G L，Liel A B，Deierlein G G，et al. Component model calibration for cyclic behavior of a corrugated shear wall[J]. Thin Walled Structures，2014，75(2)：53-62.

［17］ Zhao Qiuhong，Sun Junhao，Li Yanan，et al. Cyclic analysis of corrugated steel plate shear walls[J]. Structural Design of Tall＆ Special Bulidings，2017，26(16)：1-17.

［18］ Timler P A，Kulak G L. Experimental Study of Steel Plate Shear Walls[D]. Edmonton：University of Al-berta，1983.

［19］ Tong Jingzhong，Guo Yanlin. Elastic buckling behavior of steel trapezoidal corrugated shear walls with vertical stiffeners[J]. Thin Walled Structures，2015，95：31-39.

［20］ Tong J Z，Guo Y L. Shear resistance of stiffened steel corrugated shear walls[J]. Thin Walled Structures，2018，127：76-89.

［21］ Dou Chao，Jiang Ziqin，Pi Yonglin，et al. Elastic shear buckling of sinusoidally corrugated steel plate shear wall[J]. Engineering Structures，2016，121：136-146.

［22］ Dou Chao，Pi Yonglin，Gao Wei. Shear resistance and post-buckling behavior of corrugated panels in steel plate shear walls[J]. Thin Walled Structures，2018，131：816-826.

［23］ Hosseinzadeh L，Emami F，Mofid M. Experimental investigation on the behavior of corrugated steel shear wall subjected to the different angle of trapezoidal plate[J]. Structural Design of Tall & Special Buildings，2017，26(17)：1-17.

［24］ Cao Qiang，Huang Jingyu. Experimental study and numerical simulation of corrugated steel plate shear walls subjected to cyclic loads[J]. Thin Walled Structures，2018，127：306-317.

［25］ 钟鑫伟. 波形钢板剪力墙板框相互作用与受力性能分析[D]. 北京：北京交通大学，2019.

Zhong Xinwei. Plate-Frame Interaction and Mechanism Analysis of Corrugated Steel Plate Shear Wall[D]. Beijing：Beijing Jiaotong University，2019(in Chinese).

［26］ 王垆涛. 钢板剪力墙波形内嵌墙板受力性能研究和设计方法[D]. 北京：北京交通大学，2019.

Wang Lutao. Research on Mechanical Behaviour and Design Method of Corrugated Infill Plates in Steel Plate Shear Wall[D]. Beijing：Beijing Jiaotong University，2019(in Chinese).

［27］ ANSYS R15. 0. Canonsburg. PA[Z]. Pennsylvania，USA：ANSYS Inc，2013.

［28］ GB 50011—2010 建筑抗震设计规范[S]. 北京：中国建筑工业出版社，2016.

GB 50011—2010 Code for Seismic Design of Buildings[S]. Beijing：China Architecture & Building Press，2016(in Chinese).

Lateral Resistance Behavior Analysis of Shear Panels in Trapezoidal Corrugated Steel Shear Walls

Dou Chao，Zhu Yangze，Xie Cheng，Xie Zhidong，Yang Na

(School of Civil Engineering，Beijing Jiaotong University，Beijing 100044，China)

Compared to ordinary steel shear walls with flat infill plates(FSSWs)，the lateral resistance behavior and design of steel corrugated shear walls(SCSWs)require further investigation. Finite element analysis was used to ana-lyze the lateral resistance and load-carrying mechanism of trapezoidal corrugated shear panels in SCSWs. First，by comparing the lateral resistance of trapezoidal and sinusoidal corrugated panels，we conclude that the trapezoidal corrugated panel has better lateral resistance performance than the sinusoidal corrugated panel. Moreover，better per-formance can be achieved by increasing the inclined angle. The orthogonal numerical test is conducted to investigate the effects of the corrugation parameters(i.e.，/，/，/1，and)on the maximum and post-buckling shear resistance of infill panels；the results show that the aspect ratio and inclined angle have the most significant effect on the lateral resistance performance. Second，by comparing the inner force distribution in the boundary frame between SCSWs and FSSWs，we observe two different load-carrying mechanisms of infill corrugated panels. Additionally，a properly designed corrugated shear panel has stable post-buckling lateral resistance and exhibits in-plane shear yield-ing under lateral load. For corrugated panels with unstable post-buckling strength，the boundary columns endure sig-nificant unfavorable bending moments，which compromise the structural performance. In the case of SCSWs with large aspect ratio，the out-of-plane displacement can be reduced using vertical corrugation. Furthermore，the yield-ing zone can be fully developed，which results in better lateral resistance performance. Finally，fitting equations for the maximum shear resistance and design recommendations for stable post-buckling strength are established by ana-lyzing the lateral resistance of corrugated panels within the practical range in engineering application. The pushover ductility can be improved by reducing the normalized aspect ratio of panels. The in-plane shear yielding mechanism can be achieved in corrugated shear panels designed according to the proposed criteria.

corrugated steel shear wall；lateral resistance mechanism；shear resistance；post-buckling strength；design recommendation

TU391

A

0493-2137(2021)09-0982-09

10.11784/tdxbz202005027

2020-05-12；

2020-07-07.

窦 超（1984—  ），男，博士，副教授，douchao@bjtu.edu.cn.

朱仰泽，zhuyangze@bjtu.edu.cn.

国家自然科学基金资助项目(51808032)；中央高校基本科研业务费资助项目(2020JBM041).

Supported by the National Natural Science Foundation of China(No. 51808032)，the Fundamental Research Funds for the Central University (No. 2020JBM041).

(责任编辑：许延芳)