具有轴向动态约束的NURBS路径进给速度规划

董靖川，郭健鑫，刘 喆，谭志兰，王太勇

具有轴向动态约束的NURBS路径进给速度规划

董靖川，郭健鑫，刘 喆，谭志兰，王太勇

(天津大学机械工程学院，天津 300354)

在传统速度规划方法中，轴向加速度约束通常是定值约束，不能充分发挥机床轴向加减速性能，影响加工效率．对此提出了一种新的考虑轴向加速度动态约束的进给速度规划算法．首先，对NURBS曲线路径进行弧长自适应二分离散处理，获得弧长参数和采样点．之后，构建切向速度、加速度、加加速度约束和轴向加速度动态约束的优化模型，对采样点的多约束模型进行两次线性规划求解，得到采样点的优化进给速度．通过两次线性规划和轴向转矩参考处理，计算各轴在不同速度下的加速度上下极限动态约束，在提高加工效率同时没有增加搜索最优值的约束条件，具有较高计算效率．最后，对采样点进行样条拟合得到进给速度规划曲线．与传统定值约束规划对比实验的结果表明，所提算法牺牲最大轮廓误差2.63%，使加工时间降低了16.34%，提高加工效率的同时并没有牺牲较大精度，证明了算法的可行性和有效性．

NURBS曲线路径；进给速度规划；线性规划；轴向动态约束

非均匀有理B样条(non-uniform rational B-splines，NURBS)具有精确的形状表达和控制能力，在计算机辅助设计和数据交换领域成为了标准[1]．在数控加工领域，NURBS参数插补相比传统的线性插补，提供更加平滑和连续的运动，提高进给速度和加工精度[2-3]，并且还能减少CAD/CAM和数控系统之间数据传输负担，已经成为现代高档机床的标志．

目前，带前瞻和相应约束的加减速控制规划[4-6]是高效进给速度规划的一种方式．Yeh等[7]和Xu等[8]基于弓高误差和曲率进行自适应进给速度规划，算法能保证加工效率和加工精度，但没有考虑机床的运动学性能．Heng等[9]等提出了一种基于梯形加减速连续平滑进给策略．刘献礼等[10]提出了一种基于S型加减速寻回NURBS 插补实时算法．Dong等[5]提出一种具有前瞻规划单元模块的S型加减速连续平滑进给规划算法．但基于切向速度方向的加减速规划方式仍有以下不足：速度约束极限只在几何(曲率)极值点处，没有对其他位置进行约束，尤其是曲率大的区域；没有考虑各轴的运动学约束，在机床实际使用中各轴动态参数往往不匹配，无法充分发挥机床的加工能力；速度函数嵌入数控系统当中，导致速度规划曲线相对固定，速度规划不够灵活充分．

进给速度规划问题可以看作是具有多运动约束条件下的最小循环时间问题[11-13]，是一个值得研究且复杂的非线性优化[14]问题．最优规划起初应用在飞行器和机器人[15-16]轨迹规划领域，之后有学者在数控加工领域引入了时间最优速度规划．Zhou等[17]建立了最小时间进给的线性数学模型，利用线性规划算法(LP)求解，但未考虑轴加加速度约束；Liu等[18]对此进行了改进．Ye等[19]建立了时间最优进给速度的非线性数学模型，并利用近似解来提高计算效率，进行多次LP求解．但在大部分文献报道中轴向加速度约束都取为定值，文献[20-21]指出了轴向动态特性，将轴向加速度约束设为定值，约束不够精准．Zhang 等[20]考虑轴向动态特性引入构建了驱动电压约束，但同时也增加了搜索最优值约束条件，无形中增大了算法的开销且没有考虑加加速度约束．

针对以上问题，本文从时间最优角度开发了一种具有轴向动态约束且兼顾算法效率的进给速度规划算法.

1 NURBS曲线路径预处理

1.1 NURBS曲线定义

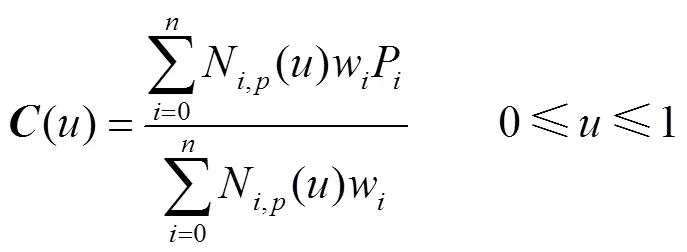
1.2 基于弧长自适应二分法的NURBS离散化

在为伺服控制器生成指令位置前，应首先在线或离线规划与编程NURBS参数路径相关联的进给速度曲线．由于曲线参数和弧长之间的非线性关系，对于一般NURBS的参数曲线来说，不能求得弧长的解析解[2]．数值方法可应用于求解NURBS弧长，如梯形公式、Simpson公式和Gauss-Lobatto积分公式．考虑计算效率和计算精度采用Simpson方式．

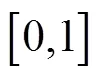
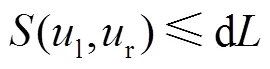
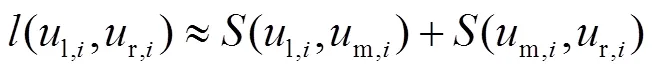
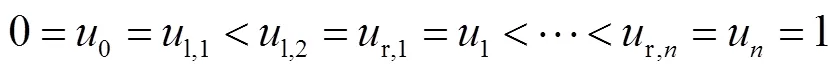
基于弧长自适应二分法的NURBS离散方法通过两个弧长限制参数，在获得采样点同时，较高精度计算出采样点之间的弧长参数．在式(4)约束下，给定合适值，可控制大曲率区域采样点密集，但在直线或者曲率较小的区域，约束会失效．如图1(a)所示，NURBS直线(长为84.86mm)仅在参数限制下获得6个采样点，严重影响计算精度，在参数共同限制下，可获得217个采样点保证了计算精度．加入式(5)约束，控制直线或者曲率较小的区域内的采样点密度．图1(b)为蝴蝶形NURBS轨迹在和共同约束下获得的采样点情况，弧长为382.86mm，采样点数目为1828．

1.3 采样点速度极限

得到每个采样点的速度极限集合

2 采样点多约束模型

2.1 切向运动学约束

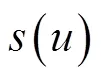
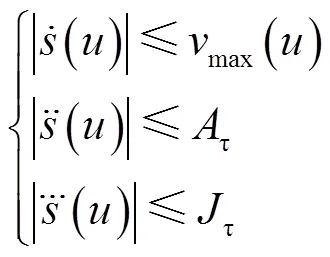
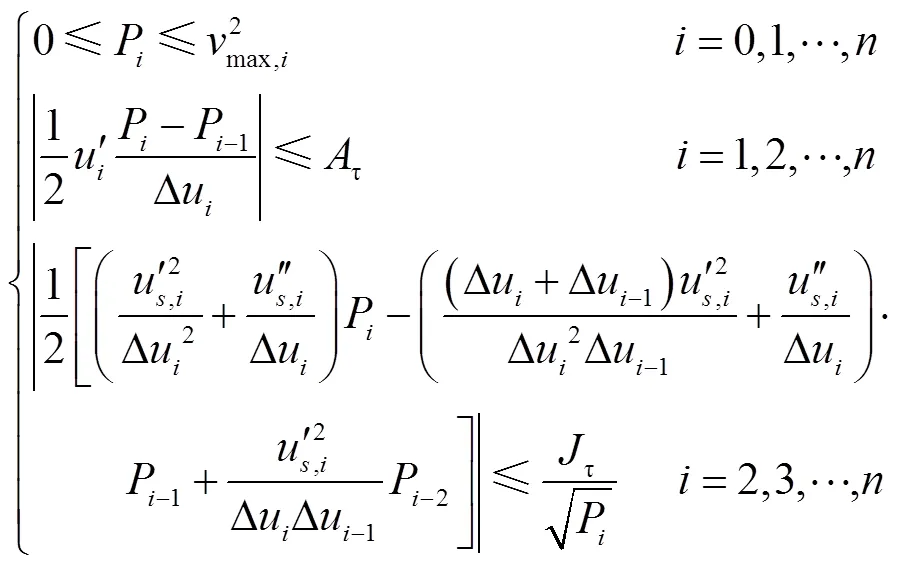
2.2 轴向加速度动态约束

数控机床的每个轴一般是由伺服电机连接滚珠丝杠传动机构驱动．伺服驱动系统中执行器输出转矩必然受到限制．假设进给轴是理想的二阶动态系统，忽略电气时间常数和库伦摩擦的影响，进给轴转矩动态平衡[21]满足

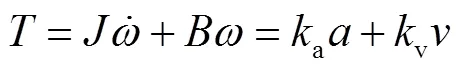
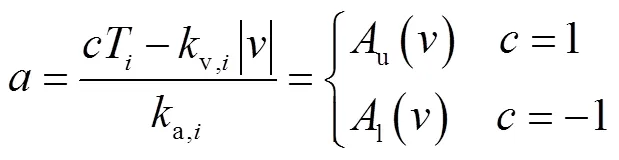
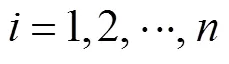
由式(15)和(19)，则考虑切向速度、加速度、加加速度约束和轴向加速度动态约束的进给速度优化的数学模型表示为

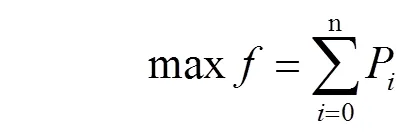
3 模型求解和进给速度规划算法

3.1 模型求解

采用线性规划方式对多约束进给速度优化的数学模型(20)求解．模型中(a)和(b)约束条件是线性的可直接应用成熟的线性规划算法求解．考虑算法效率，线性规划求解算法采用内点法．约束条件(c)和(d)不能直接应用，需要线性化．本文采用两次线性规划求解模型，步骤如下．

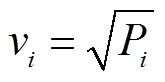
3.2 进给速度规划算法

提出的算法主要有3个部分：NURBS曲线预处理处理、两次线性规划、进给速度样条拟合．主要工作包括：对NURBS曲线进行弧长自适应二分获取采样点以及计算弧长参数；构建约束模型；数值计算模型中的所需参数；对模型进行两次线性规划；对采样点的进给速度样条拟合．算法流程图如图2所示．

算法概述步骤如下．

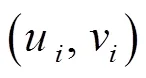
图2 进给速度规划算法流程

4 实 验

4.1 实验平台

实验平台如图3所示，轴向进给机构是由永磁同步伺服电机(PMSM)基于驱动滚珠丝杠副实现工作台移动，伺服电机型号为三菱HC-UFS13，伺服驱动器为三菱MR-J2S-10A．控制器算法是在Matlab/ Simulink软件中开发的，轴控制器模型如图4所示，由外部的位置环和内部的速度环组成，位置环是比例(P)型控制器，速度环是一个比例积分(PI)型控制器．实时控制部分采用Simulink Desktop Real-Time库实现，保证实时性能．计算机和定制接口板通过以太网UDP协议交换实时数据．定制的接口板配备了ARM STM32F407ZGT6微控制处理器，用来连接实时控制计算机和伺服驱动器．将驱动器设置为转矩控制模式，控制器产生转矩模拟信号指令并采集反馈的电机编码器信号，在控制器中实现闭环控制.

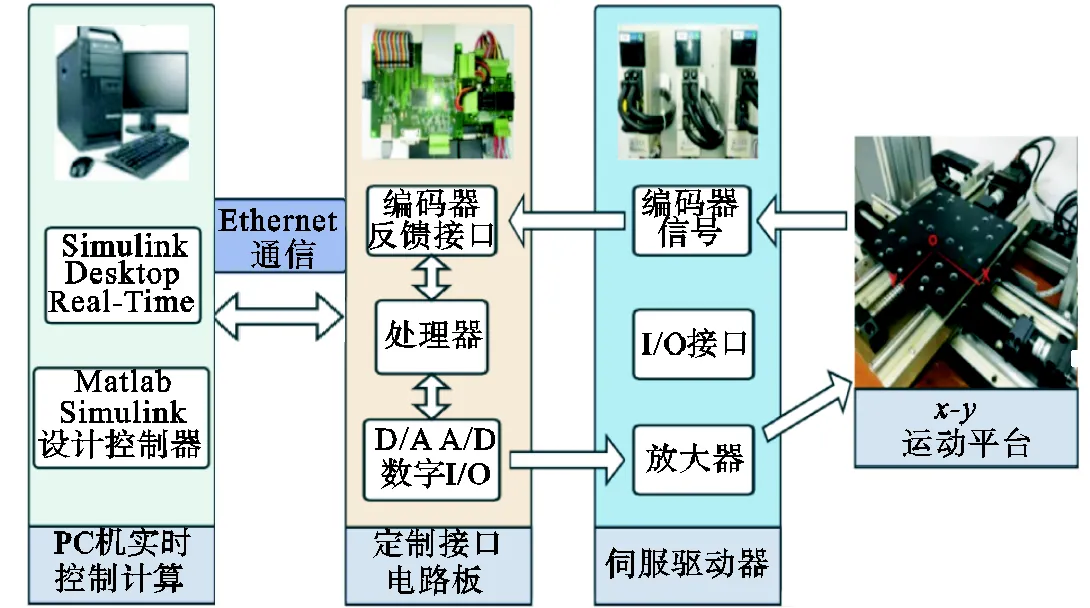
图3 实验平台

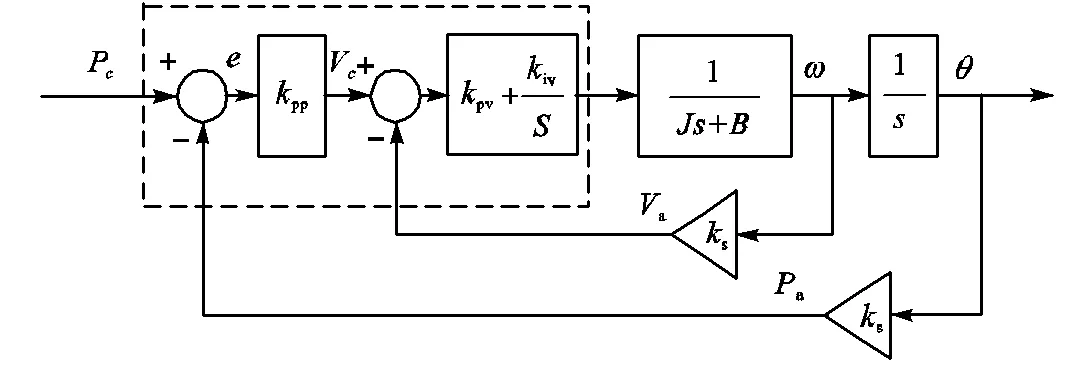
图4 轴控制器模型

4.2 实验结果分析

为了验证算法的可行性和有效性，选取3阶蝴蝶形状NURBS参数曲线路径作为实例进行实验验证，如图5所示，曲线有低曲率区和高曲率区，曲线变化相对复杂．实验参数预置如表1所示，表中各轴惯性质量和黏性摩擦通过系统辨识获得．规划结果通过NURBS插补生成时间-位置序列，将其作为伺服指令输入进行实验验证，下个插补点通过式(22)计算．

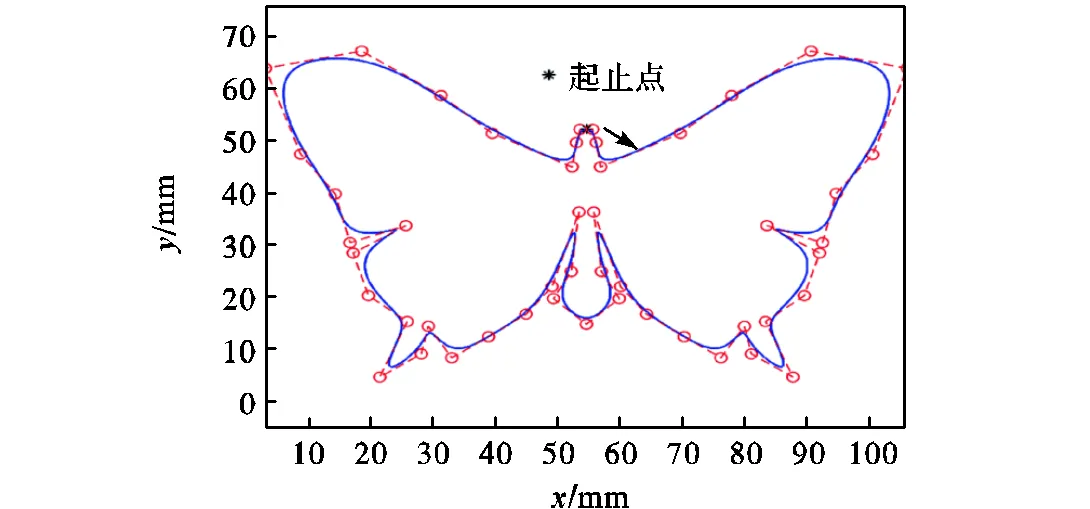
图5 蝴蝶形NURBS轨迹

表1 实验参数

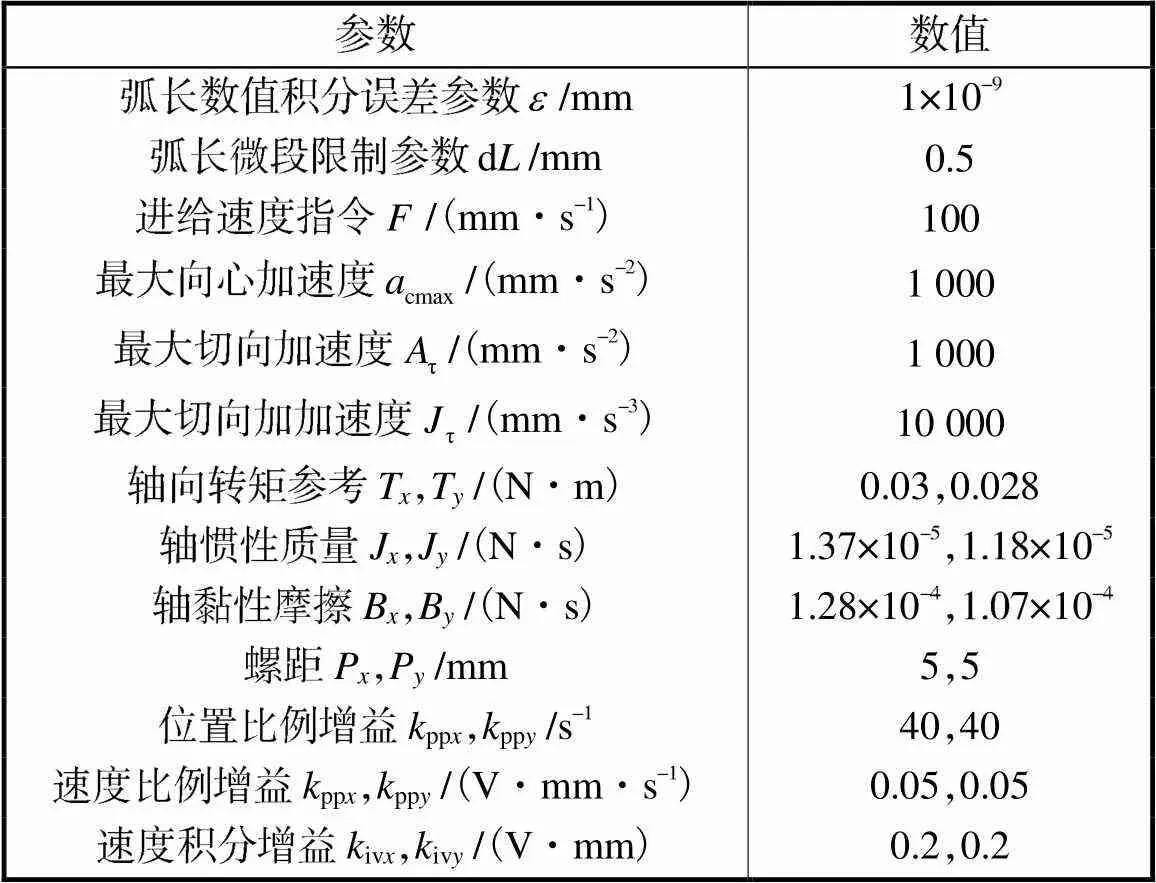
Tab.1 Test parameters

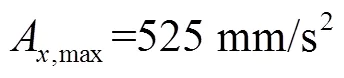
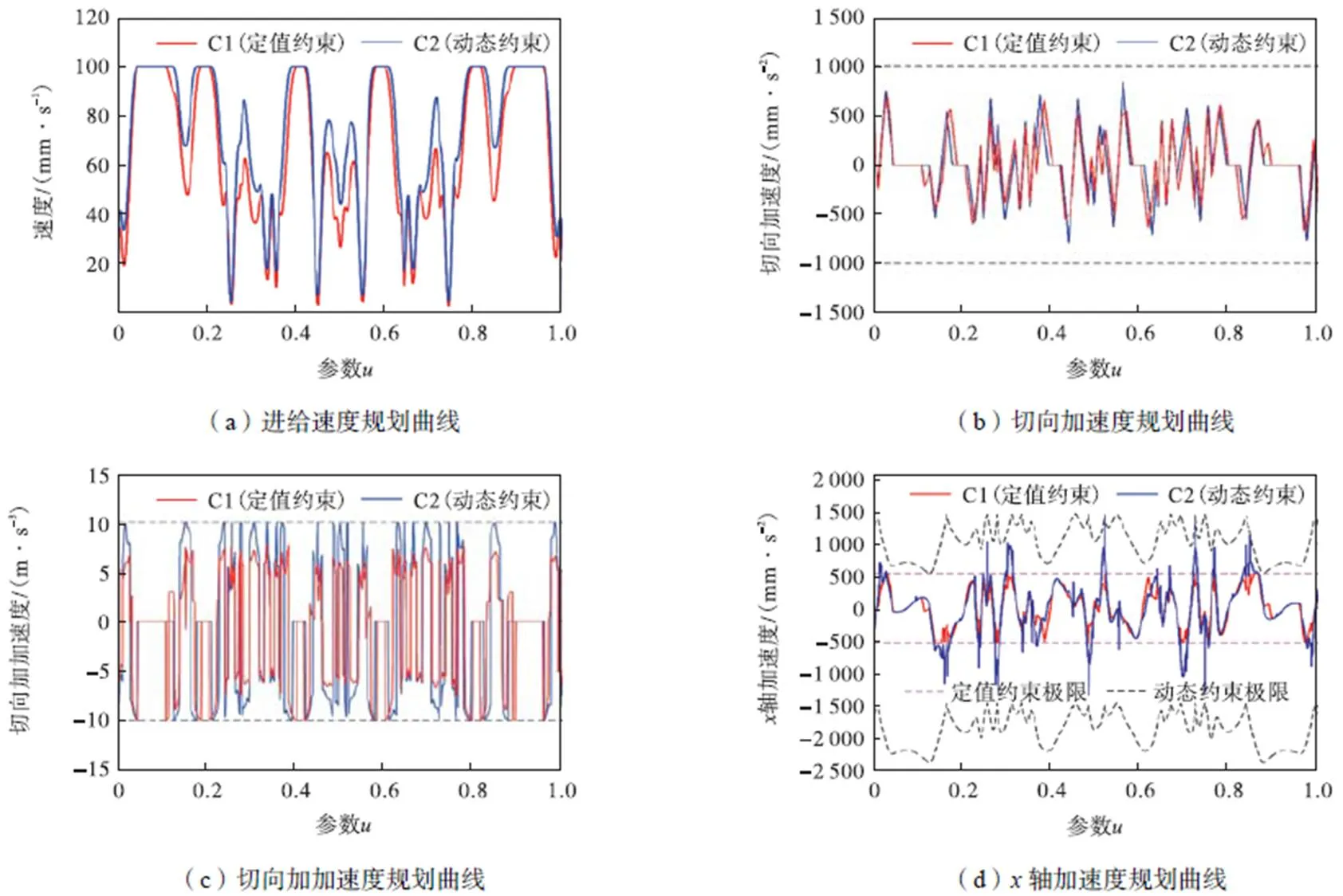
图6(a)～(c)分别为C1和C2的进给速度、切向加速度和切向加加速度规划曲线，可以看出切向的运动学被约束在极限之内．图6(d)和图6(e)分别为C1、C2的轴加速度和轴加速度规划曲线，其中C2各轴的加速度基本被约束在相应动态约束极限内，与C1相比，C2动态约束规划在低速下可规划相对更大的加速度值．图7为实验C1、C2各轴的实际速度和加速度曲线，可以看出在曲线极值处C2实际速度和加速度值比C1的值更大，证明了本文所提的具有轴向动态约束的规划算法的有效性．

弧长数值积分误差限制参数和弧长微段限制参数，两者参数数值选取越小，获得采样点数目越多，计算精度会提高，但也会带来较大计算开销．图8为不同采样点规划图像，可以看出合理的采样点数目可以较好表达出速度变化，并且最终规划的时间误差在2%之内，综合考虑计算精度和计算效率，选取本文的两者参数(数据点为1828，规划时间为6.51s)．

图9(a)为C1和C2的运动过程振动信号，并统计其均方根值(root mean square，RMS)，其中C1为0.0116，C2为0.0129．图9(b)为C1和C2的实际运动轨迹，图9(c)为C1和C2的实际运动轨迹和参考轨迹之间轮廓误差，表2为统计C1和C2的轮廓误差的最大值(maximum，MAX)和RMS值．其中，实验C1加工时间为7.784s，C2的加工时间为6.512s，与C1传统定值约束相比，所提算法轮廓误差MAX升高2.63%，RMS升高5.57%，加工时间降低16.34%，提高了加工效率同时并没有牺牲较大的精度．实验C2算法在2.2GHz CPU的PC机上运行，规划蝴蝶形轨迹，采样点数目为1828，算法计算时间约为2.20s，远小于实际加工时间，为在线规划提供了可能性．

表2 C1和C2轮廓误差对比统计

图9 C1和C2的精度对比

5 结 论

本文针对NURBS参数曲线路径，为充分发挥机床轴向加减速性能，提出一种新的具有轴向动态约束的进给速度规划算法．通过实验分析和验证得出以下结论．

(1) 在预处理阶段，对NURBS加工路径进行弧长自适应二分离散处理，通过弧长限制参数，在离散化过程同时，获得较高精度弧长参数．

(2) 在规划阶段，提出一种新的考虑轴向动态约束算法解决方案．在具有一般运动学约束条件(切向速度、加速度、加加速度)的基础上，通过两次线性规划和转矩参考处理，在没有增加搜索最优值的条件下引入轴向加速度动态约束．该方案有效利用了进给电机的潜力，提高加工效率同时具有较高计算效率．

［1］ Piegl L，Tiller W. The NURBS Book[M]. New York：Springer，1997.

［2］ Min Liu，Huang Yu，Yin Ling，et al. Development and implementation of a NURBS interpolator with smooth feedrate scheduling for CNC machine tools[J]. International Journal of Machine Tools and Manufacture，2014，87：1-15.

［3］ 何改云，陶 浩，王太勇，等. 连续时间周期化的NURBS曲线插补及其速度规划[J]. 天津大学学报：自然科学与工程技术版，2018，51(8)：844-853.

He Gaiyun，Tao Hao，Wang Taiyong，et al. Continuous to periodic time NURBS curve interpolation and its speed planning[J]. Journal of Tianjin University：Science and Technology，2018，51(8)：844-853(in Chinese).

［4］ 罗福源，游有鹏，尹 涓. NURBS曲线S形加减速双向寻优插补算法研究[J]. 机械工程学报，2012，48(5)：147-156.

Luo Fuyuan，You Youpeng，Yin Juan. Research on the algorithm of NURBS curve bidirectional optimization Interpolation with S-type acceleration and deceleration control[J]. Chinese Journal of Mechanical Engineering，2012，48(5)：147-156(in Chinese).

［5］ Dong Jingchuan，Wang Taiyong，Li Bo，et al. Smooth feedrate planning for continuous short line tool path with contour error constraint[J]. International Journal of Machine Tools and Manufacture，2014，76：1-12.

［6］ 李 浩，吴文江，韩文业，等. 基于自适应前瞻和预测校正的实时柔性加减速控制算法[J]. 中国机械工程，2019，30(6)：690-699.

Li Hao，Wu Wenjiang，Han Wenye，et al. Real-time flexible acceleration and deceleration control algorithm based on adaptive look-ahead and predictor-corrector method[J]. China Mechanical Engineering，2019，30(6)：690-699(in Chinese).

［7］ Yeh S S，Hsu P L. Adaptive-feedrate interpolation for parametric curves with a confined chord error[J]. Computer-Aided Design，2002，34(3)：229-237.

［8］ Xu Zhiming，Chen Jincheng，Feng Zhengjin. Performance evaluation of a real-time interpolation algorithm for NURBS curves[J]. International Journal of Advanced Manufacturing Technology，2002，20(4)：270-276.

［9］ Heng M，Erkorkmaz K. Design of a NURBS interpolator with minimal feed fluctuation and continuous feed modulation capability[J]. International Journal of Machine Tools and Manufacture，2010，50(3)：281-293.

［10］ 刘献礼，周肖阳，李茂月，等. NURBS曲线S形加减速寻回实时插补算法[J]. 机械工程学报，2017，53(3)：183-192.

Liu Xianli，Zhou Xiaoyang，Li Maoyue，et al. The real-time algorithm of NURBS curve retriever interpolation with S-type acceleration and deceleration control [J]. Chinese Journal of Mechanical Engineering，2017，53(3)：183-192(in Chinese).

［11］ Zhang Q，Li S R. Efficient computation of smooth minimum time trajectory for CNC machining[J]. The International Journal of Advanced Manufacturing Technology，2013，68(1)：683-692.

［12］ Guo Jianxin，Zhang Qiang，Gao Xiaoshan，et al. Time optimal feedrate generation with confined tracking error based on linear programming[J]. Journal of Systems Science and Complexity，2015，28(1)：80-95.

［13］ 浦玉学，舒鹏飞，蒋 祺，等. 工业机器人时间-能量最优轨迹规划[J]. 计算机工程与应用，2019，55(22)：86-90.

Pu Yuxue，Shu Pengfei，Jiang Qi，et al. Time-energy optimum trajectory planning for industrial robot[J]. Computer Engineering and Applications，2019，55(22)：86-90(in Chinese).

［14］ Zhang Qiang，Li Shurong，Guo Jianxin，et al. Time-optimal path tracking for robots under dynamics constraints based on convex optimization[J]. Robotica，2016，34(9)：2116-2139.

［15］ 罗 翔，沈 洁，毛玉良，等. 存在驱动饱和约束下的机器人时间最优实时运动规划研究[J]. 机器人，2001(1)：26-30.

Luo Xiang，Shen Jie，Mao Yuliang，et al. Real-time motion planning research of robots due to the limited actuation power[J]. Robotics，2001(1)：26-30(in Chinese).

［16］ 徐海黎，解祥荣，庄 健，等. 工业机器人的最优时间与最优能量轨迹规划[J]. 机械工程学报，2010，46(9)：19-25.

Xu Haili，Xie Xiangrong，Zhuang Jian，et al. Global time-energy optimal planning of industrial robot trajectories[J]. Chinese Journal of Mechanical Engineering，2010，46(9)：19-25(in Chinese).

［17］ Zhou Jianfeng，Sun Yuwen，Guo Dongming. Adaptive feedrate interpolation with multiconstraints for five-axis parametric toolpath[J]. The International Journal of Advanced Manufacturing Technology，2014，71(9/10/11/12)：1873-1882.

［18］ Liu Huan，Liu Qiang，Yuan Songmei. Adaptive feedrate planning on parametric tool path with geometric and kinematic constraints for CNC machining[J]. The International Journal of Advanced Manufacturing Technology，2017，90(5/6/7/8)：1889-1896.

［19］ Ye Peiqing，Zhang Yong，Xiao Jianxin，et al. A novel feedrate planning and interpolating method for parametric toolpath in Frenet-Serret frame[J]. The International Journal of Advanced Manufacturing Technology，2019，101(5)：1915-1925.

［20］ Zhang Yong，Ye Peiqing，Zhao Mingyong，et al. Dynamic feedrate optimization for parametric toolpath with data-based tracking error prediction[J]. Mechanical Systems and Signal Processing，2019，120：221-233.

［21］ Dong J，Stori J A. Optimal feed-rate scheduling for high-speed contouring[J]. J Manuf Sci E：T ASME，2007，129(1)：63-76.

［22］ Mathews J H，Fink K D. Numerical Methods Using MATLAB[M]. Upper Saddle River：Prentice Hall，1999.

Feedrate Planning of a NURBS Path with Dynamic Axial Constraints

Dong Jingchuan，Guo Jianxin，Liu Zhe，Tan Zhilan，Wang Taiyong

(School of Mechanical Engineering，Tianjin University，Tianjin 300354，China)

In conventional feedrate planning，the axial acceleration constraint is usually a fixed value constraint，which cannot efficiently use the acceleration capacity of the axes of the machine tools and affects the machining effeciency. A new feedrate planning algorithm considering the dynamic constraint of axial acceleration is proposed. First，the non-uniform rational B-splines curve path is processed by adaptive dichotomous discretization to acquire the arc length parameters and sampling points. Then the optimizing model is constructed with the tangential velocity，acceleration，jerk，and dynamic axial acceleration constraints. A two-stage linear programing is applied to the multi-constraint optimizing model on the sampling points to find the points’ optimal velocity. The dynamic constraints of the upper and lower limits of the acceleration of each axis at different velocities are obtained through the two-stage linear programing and the reference axial torque，which improves the processing efficiency without increasing the constraint condition of searching the optimal value，thus ensuring high computation efficiency. Finally，the sample points are fitted with a spline to obtain the feedrate planning curve. In a comparative experiment with the conventional fixed constraint planning，the proposed algorithm sacrifices 2.63% of the maximum contour error，reduces the processing time by 16.34%，and improves the processing efficiency without sacrificing much precision，which proves the feasibility and effectiveness of the algorithm.

NURBS path；feedrate planning；linear programing；dynamic axial constraint

TP273

A

0493-2137(2021)09-0890-09

10.11784/tdxbz202006045

2020-06-16；

2020-09-24.

董靖川（1983—  ），男，博士，高级工程师，jcdong@tju.edu.cn.

郭健鑫，jxguo@tju.edu.cn.

国家自然科学基金资助项目(51605328)．

Supported by the National Natural Science Foundation of China(No. 51605328)．

(责任编辑：王晓燕)