可重构机床多目标优选方法

王太勇，孙熙冉，田松龄，张 雷，马明珠

可重构机床多目标优选方法

王太勇1, 2，孙熙冉1，田松龄3, 4，张 雷5，马明珠1

(1. 天津大学机械工程学院，天津 300350；2. 天津大学仁爱学院，天津 301636；3. 天津城建大学控制与机械工程学院，天津 300384；4. 天津市泰森数控科技有限公司，天津 300392；5. 天津商业大学机械工程学院，天津 300134)

模块化的可重构机床使可重构制造系统具备高效生产零件族的能力，对可重构制造系统的可重构能力和响应能力有着显著影响．为设计一个低成本、高可重构能力的可重构制造系统，提出了一种基于布谷鸟搜索算法的可重构机床多目标优选方法．首先，通过加工方向建立加工工序与可重构机床的映射关系．其次，考虑到制造系统生产零件族中不同零件时需进行重构，对可重构机床进行标识以清晰地表述可重构制造系统重构过程中可重构机床的变化．再次，从设备级和系统级两个层级分别量化了重构过程中的重构成本和重构指数，并基于此提出了两个目标函数：最小化可重构制造系统设计总成本和最大化总重构指数．最后，通过工程实例来验证该方法的有效性和高效性．案例结果表明：得到的设计成本最低的方案值为316.7，最佳的重构指数方案的值为27.4．此外，与解决此类问题常用的多目标优化算法NSGA-Ⅱ比较，多目标布谷鸟搜索(MOCS)算法能快速收敛并在200次迭代后取得全局的Pareto最优解，证明了提出的方法能够高效地筛选出更经济、更高重构指数的可重构机床选择方案．所提出的多目标优选方法可为后续的相关研究和生产实践提供指导．

可重构机床；可重构制造系统；机器选择；多目标布谷鸟算法

当前，在市场环境与客户需求不断变化的背景下，可重构制造系统[1](reconfigurable manufacturing system，RMS)因其高度可重构能力[2]和响应能力[3]脱颖而出．可重构机床(reconfigurable machine tool，RMT)是为定制化加工需求而设计的[4]，与普通数控机床相比，具有结构灵活可变和综合收益高等特点[5].当加工需求发生变化时，RMT可以以最经济、有效的方式进行重构．因此，RMT被认为是RMS的核心设备[6]，将直接影响RMS的可重构能力和对变化需求的响应能力．因此，有必要对RMT进行优选．

Bensmaine等[7]研究了RMS设计过程中RMT的选择问题，考虑了最小化总设计成本(生产成本、重构成本、换刀成本和刀具使用成本)和最小化完工时间两个目标，并提出了一种改进的非支配排序遗传算法(non-dominated sorted genetic algorithm-Ⅱ，NSGA-Ⅱ)解决了该问题．Dahane等[8]研究了在机器可靠性约束下的RMT选择问题，考虑了总最小化设计成本(使用成本、维护成本)和最大化RMS重构指数两个目标．Benderbal等[9]研究了在设备故障的约束条件下的RMT选择问题，考虑了最大化系统柔性指数和最小化完工时间两个目标，并采用NSGA-Ⅱ和理想解相似性参考排序技术(technique for order preference by similarity to an ideal solution，TOPSIS)求解该问题．Benderbal等[10]在其后续的研究中提出了用于量化RMS模块性的模块性指数，分别考虑了最大化模块性指数、最小化完工时间和最小化设计成本3个目标，并采用了改进的存档多目标模拟退火算法(archive multi-objective simulated annealing，AMOSA)和TOPSIS来解决该问题．然而，上述研究中只考虑为单个零件的生产选择合适的RMT，而不是整个零件族，忽略了零件族中不同零件加工时RMS的重构过程对RMT选择的影响．Huang等[11]提出了一种基于零件族划分和设备选型的延迟可重构制造系统(delay reconfigurable manufacturing system，D-RMS)设计方法．然而，其研究仅从专用机床、柔性机床、可重构机床中选择合适的设备类型来设计D-RMS，而不是选择特定具体的设备．Ming 等[12]提出了一种基于RMT本体的RMT模块选择方法，建立了表示特征、工序和RMT模块3个概念的分类、属性和因果关系的知识库，并利用知识库中的编码来选择合适的RMT模块．然而，其研究仅根据RMT设备层次指标研究了RMT模块选择，而忽略了RMS系统层次指标对RMT模块选择的影响．

本研究从一组候选的RMT集合中选择最佳RMT子集的问题，这些RMT将集成到RMS中并用于零件族的生产．首先，基于RMT原型建立了工序与RMT的映射关系并得到候选RMT表．其次，建立RMT标识表，从设备级和系统级两个层级清晰地表述RMS重构过程中RMT的变化，用设计总成本和重构指数将重构过程定量化表达，对RMT优选问题进行建模．最后，应用启发式多目标布谷鸟搜索算法(multi-objective cuckoo search，MOCS)对模型求解并给出案例．

1 问题描述与模型构建

1.1 问题描述

RMT原型由基座模块、加工模块和工作台模块组成[13]，如图1所示，其中基座是固定部件，由与重构无关的组件构成．而加工模块和工作台是可重构部件，由一些可重构组件构成，这些可重构组件可以根据加工要求进行添加、删除、替换等．RMT各模块的特点如下．

(1) 基座用于安装加工模块和工作台模块，组件间采用标准接口进行连接[14]．由于不同基座装载模块组件的能力不同，因此不同的RMT加工能力也不同，由此可根据基座区分RMT．同一台RMT可通过添加、删除、或替换可重构组件来改变RMT的加工能力．

(2) 加工模块由主轴、滑轨、转台、立柱等组件构成，不同组件组合形成的加工模块可使RMT具备不同的加工方向，加工方向矩阵MD＝[T，T，T，R，R，R]．其中T和R分别表示沿轴移动和绕轴旋转．

(3) 工作台模块则由夹具及平台等组件构成．夹具是为特定零件设计的定制化组件，用于零件的定位和夹紧．平台可调节加工零件的位姿，与加工模块配合，可满足零件特定加工位置的加工要求．

图1 RMT原型

由于工作台模块主要用于零件的定位夹紧及位姿的调节，与加工模块相互独立，所以可通过加工方向建立工序与RMT的映射关系，将加工工序分配给RMT．如图1所示，将由一些可重构组件组成的加工模块安装在RMT基座上后，RMT会提供与加工模块相应的加工方向．只有当RMT提供零件加工工序所需的加工方向，工序才能分配给该RMT．根据工序与RMT 的映射关系，建立候选RMT矩阵表，该表表示零件族中每个零件的每道加工工序的候选RMT，示例如表1所示．根据该表，为零件族中每个零件的每道工序从候选的RMT集合中选择最佳的RMT．

表1 工序的候选RMT

Tab.1 Candidate RMT for operations

1.2 模型构建

为设计一个低成本、高可重构能力及响应能力的RMS，在优选RMT过程中，分别考虑了最小化RMS设计总成本和最大化RMS重构指数两个目标函数．RMS重构指数表示RMS快速重构以制造零件族中的其他零件的能力．重构指数越高，重构的工作量越小，RMS重构能力和响应能力越强．

1.2.1 RMT类型标识

RMS重构可分为系统级的RMS重构(添加、卸载RMT)和设备级的RMT重构(添加、卸载模块组件)两种重构类型．其中，RMT可分为系统级重构的RMT和设备级重构的RMT两种设备类型．两个目标函数均与RMS重构过程RMT的变化有关，因此，需对RMT进行类型标识以清晰地表述RMS重构过程中RMT的变化．

(1) RMS重构前后不同的RMT会被标识符“1”标识．

(2) RMS重构前后同一台RMT会根据重构成本进一步确定RMT的标识符．

图2 RMT标识

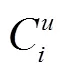
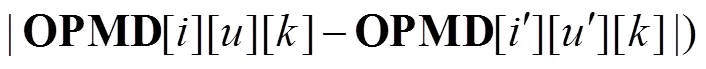
表2 RMT重构成本

Tab.2 Reconfiguration cost of the RMT

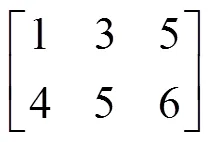
表3 RMT重构成本示例

Tab.3 Example of the RMT’s reconfiguration cost

1.2.2 RMS设计总成本

RMS设计总成本由重构成本和使用成本组成．其中重构成本与RMS重构过程中RMT的变化有关，使用成本与待加工工序的加工时间及使用的基座模块与加工模块有关．

1) 重构成本

重构成本由系统级的RMS重构成本和设备级的RMT重构成本组成．

式中：RC为重构成本；RCRMS为系统级的RMS重构成本；RCRMT为设备级的RMT重构成本.

式中CCB[]为安装或卸载基座的成本；NP为零件族中零件总数量；OPTN为零件P的工序总数量；RMT为候选的RMT总数量；Mod为加工模块的总数量.

2) 使用成本

使用成本由基座模块的使用成本和加工模块的使用成本组成．

式中：UC为RMT的使用成本；PrTime[][]为零件P的工序Op的加工时间；UCB[]为基座的使用成本；UCMod[]为加工模块的使用成本；MOP[][][]为RMT与工序的关系.

因此，目标函数RMS设计总成本TotalCost表示为

1.2.3 RMS重构指数

RMS的重构指数与重构过程中的工作量有关，由系统级的RMS重构指数及设备级的RMT的重构指数组成．

1) 设备级的RMT重构指数

设备级的RMT重构指数与可以安装在其上的组件数量和重构工作量有关．图3及式(8)详细说明了设备M重构工作量的计算，其中NA为添加模块组件的数量，ND为移除模块组件的数量，NC为公共模块组件的数量．

图3 RMT重构工作量计算

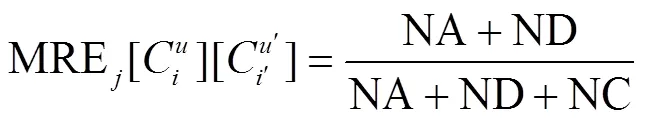
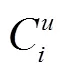
式中：RI[][][]为设备M的重构指数；MMD[][]为RMT与加工方向的映射关系矩阵.

式中RIRMT为设备级的RMT的重构指数.

2)系统级RMS重构指数

系统级RMS重构指数与候选RMT的数量和系统级重构工作量有关．图4及式(11)详细说明了RMS重构工作量的计算．其中na为添加RMT的数量，nd为移除RMT的数量，nc为公共RMT的数量，RMS为生产零件P的RMS．

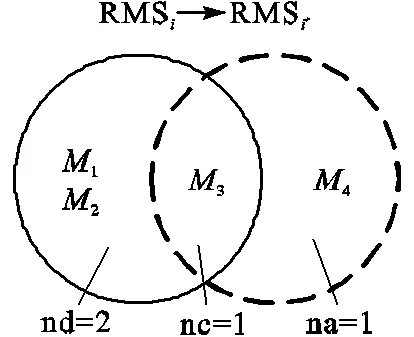
图4 RMS重构工作量计算

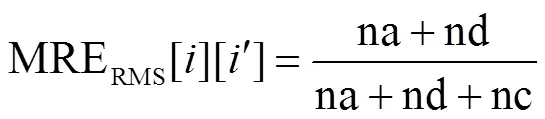
式中MRERMS[][]为RMS由RMS得到RMS的重构工作量.

式中RIRMS为系统级的RMS重构指数.

因此，目标函数RMS重构指数RI表示为

2 问题求解

2.1 RMT优选方法流程

首先，输入加工工序与加工方向的映射关系矩阵OPMD与RMT与加工方向的映射关系矩阵MMD、基座模块与加工模块的使用成本和装载成本及多目标布谷鸟搜索算法的参数．其次，建立工序与RMT的映射关系并得到工序的RMT候选表．接着，生成RMT集合随机密钥序列，通过对随机密钥的编码与解码，应用MOCS算法对模型进行求解．然后，判断该解是否属于Pareto最优解及迭代次数是否达到最大．最后，输出Pareto解集．RMT优选方法流程如图5所示．

图5 RMT优选方法流程

2.2 建立工序与RMT的映射关系

基于RMT原型，需建立工序与RMT的映射关系并建立工序的候选RMT表．因此，加工工序分配给RMT可分为3个步骤．

(1) 确定加工工序与加工方向的映射关系矩阵OPMD．

(2) 确定RMT与加工方向的映射关系矩阵MMD．

(3) 根据式(14)将加工工序分配给指定的RMT.

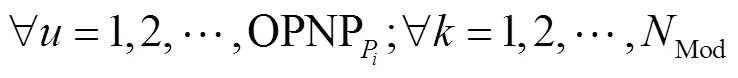
式中：MOP[][][]表示RMT与工序的关系，如果零件P的工序Op由RMT设备M的加工模块完成加工则等于1，否则为0.

图6中，加工工序Op2需要T、T、R3个加工方向，则OPMD[][]＝[0，1，1，0，1，0]．1可通过安装加工模块最多提供T、T、R、R4个加工方向，则MMD[]＝[0，1，1，1，1，0]，3可提供T、T、R3个加工方向，则MMD[]＝[0，1，1，0，1，0]，根据式(14)则得到结论为工序Op2的候选RMT为1或3．

图6 工序与RMT的映射关系

2.3 编码与解码

编码与解码是数学建模和启发式算法设计的重要步骤，对启发式算法的运行效率和有效性起着重要的作用．本例中，当MOCS算法运行时，Levy flight的应用修改了编码值[15]．为了避免修改后的编码值可能导致不可行解的出现，使用连续域随机变量来生成所有可行解的随机密钥．

图7中左上角表示第代的随机密钥，每个单元格包含一个0～1之间的随机密钥值key(key∈[0，1])，该密钥值即为RMT的编码值．通过对随机密钥的解码，生成右上角RMT集合，该集合中的元素即为每道加工工序选定的RMT．将第代随机密钥与随机生成的Levy flight值结合，生成左下角第＋1代密钥．类似地，通过对第＋1代密钥解码生成第＋1代RMT集合．

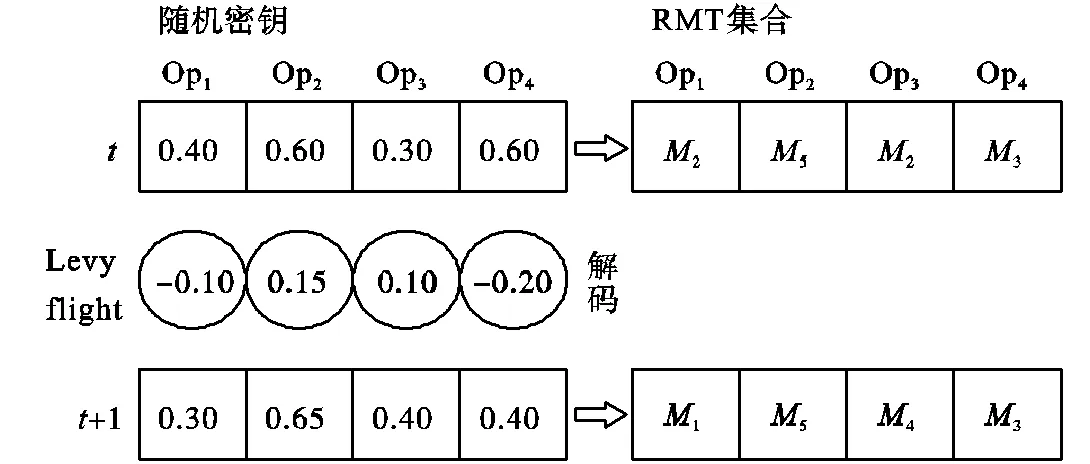
图7 编码与解码

解码过程即为确定加工每道工序所需的RMT.举例说明解码过程．示例如下．

假设零件1有4道待加工工序，根据工序和RMT之间的映射关系，已建立了候选RMT表(表4)，结合图7和表4中的第代随机密钥来说明该示例．

表4 工序的候选RMT示例

Tab.4 Example of a candidate RMT for an operation

解码过程可分为4个步骤：

(1) 确定零件的加工工序数量等于随机密钥的数量，保证为每道工序分配RMT；

(2) 建立每道工序的候选RMT列表CM．此列表的大小取决于能够完成指定工序的RMT数量；

(3) 工序对应的随机密钥值乘以该工序候选RMT的数量(即CM列表的大小)．将乘积结果向上取整，得到索引值Mindex(Mindex＝Roundup(key×length(CM)))；

(4) 获取的整数值Mindex表示要从列表CM中选择RMT的索引，并将选择的RMT添加到解码单元中．

示例：表4中，零件1的工序Op1可以分配给设备1、2或3，建立CM＝{1，2，3}．根据图7，Op1对应的第代随机密钥值为0.40．则Min- dex＝Roundup(0.40×3)＝2．得到Mindex值为2，则CM列表中的第2个元素2即为选定的RMT．

2.4 多目标布谷鸟算法

随着问题规模的增大，最优解或近优解的求解也更加困难．RMT优选问题属于典型的NP-hard问题，很难使用枚举法等精确算法解决该问题[16]．因此，本文采用一种启发式优化算法来求解该问题，即布谷鸟搜索(cuckoo search，CS)算法．CS算法是Yang等[17]在2009年首次提出的．2014年，Yang等[18]提出了一种用于多目标优化的多目标布谷鸟搜索算法，MOCS已经用精选的测试函数子集进行了测试，结果表明MOCS是一个有效的多目标优化方法．结合全局和局部两种搜索方法，多目标布谷鸟算法的伪代码如下.

多目标布谷鸟搜索算法伪代码

目标函数1()，…，f()，＝(1，…，x)T

产生个宿主巢穴/解的初始种群x，每个巢穴里产个卵/目标

While＜MaxGen(最大迭代次数) do

随机选取一只布谷鸟并通过Levy flight产生一个新解式(15)

评估巢穴nest的个解并且检验其是否属于Pareto最优解

从个巢穴中随机选择一个巢nest

评估巢穴nest的个解

if巢穴nestPareto支配nestthen

将巢穴nest取代巢穴nest

End if

以一定的概率P放弃一部分劣解并通过局部搜索产生一个新解式(18)

保存最佳巢穴(优质巢穴)

排列解找出当前非劣解

更新←＋1

End while

1) Levy flight搜索方法

Levy flight是一种随机游动随机行走、间歇性、无标度的搜索算法，其步长具有重尾概率分布．在原有点基础上叠加一个随机生成的方向和步长，从而得到新的点．但是需要指出，随机生成的方向和长度并不是完全随机的．研究发现通过Levy flight的搜索方式能有效地寻找全局最优解而不至于陷入局部最优解中．

式中：为第代解；(，)为Levy flight搜索；为一个步长标度因子；为步长；为伽马函数指数.

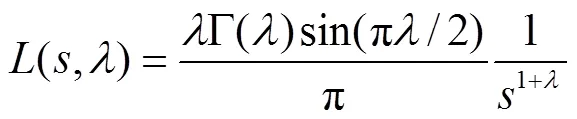
式中Γ()为伽马函数.

2) 局部搜索方法

局部搜索是另一种随机行走的搜索方法．因容易陷入局部最优解，所以这种方法只适用于局部搜索，优点是比较稳定．

相对于Levy flight的随机性，局部随机行走时具有一定的方向性，其最大程度地利用已有点的位置信息，新产生的点便是这些已有点的“折中”．

3 案例分析

假设有一个由3个零件组成的零件族，其中3个零件的加工工序数量分别为3、3、4．从8台候选的RMT集合中为零件族的生产选择最佳RMT子集．

表5表示加工每个零件的每道工序所需的加工方向及加工时间．表6表示每台RMT最多可提供的加工方向．表7表示基座模块的使用成本及重构时安装或卸载的成本．表8表示加工模块的使用成本及重构时安装或卸载的成本．表9表示MOCS算法的参数设置．表10表示优选方案，对于A、B、C ３个方案，分别给出了选定的RMT集合、RMS设计总成本和重构指数．表11表示NSGA-Ⅱ算法的参数设置．图8表示MOCS与NSGA-Ⅱ分别在不同迭代次数下取得的Pareto解．

方案A代表RMS设计成本最低的方案(316.7)．这是因为尽可能多地选择相同的RMT完成零件族的生产，其中1和2分别被选择了3次．事实上，与固定部件基座相比，可重构部件更便宜、更轻、更小，因此能够更容易实现更经济、更快的重构，选择相同的RMT可降低重构成本，进而得到更经济的选择方案．

表5 加工工序需要的加工方向

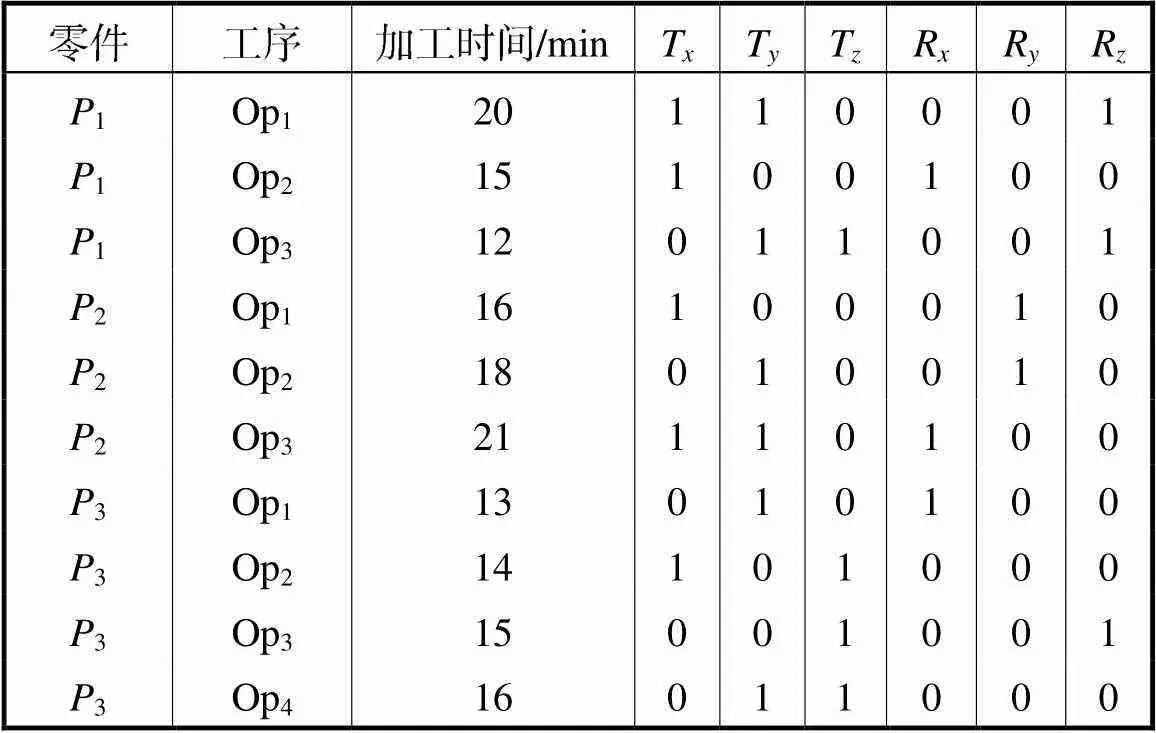
Tab.5 Machining direction required by operations

表6 RMT可提供的加工方向

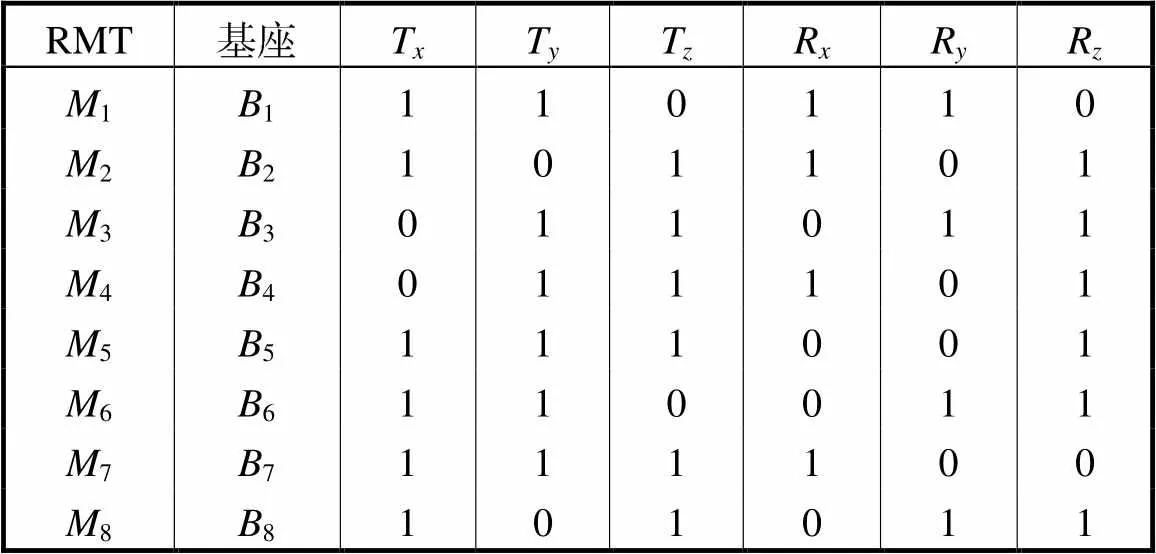
Tab.6 Machining direction provided by the RMTs

表7 基座的使用成本及装载成本

Tab.7 Usage cost of base & Install or uninstall cost of base

表8 加工模块的使用成本及装载成本

Tab.8 Usage cost and install or uninstall cost of the ma-chining module

表9 MOCS算法的参数设置

Tab.9 Parameter settings for the MOCS algorithm

表10 RMT集合优选方案

Tab.10 Scheme of the RMT set selection

表11 NSGA-Ⅱ算法的参数设置

Tab.11 Parameter setting of the NSGA-Ⅱ algorithm

图8 MOCS与NSGA-Ⅱ迭代寻优对比

然而，方案C保证了RMS最佳的重构指数(27.4)．事实上，生产零件1、2和3都选用了1和3，其中生产零件1和2更是选用了相同的RMT集合(1，3，6)，所以当生产不同零件需对RMS进行切换时，有效避免RMS的大规模重构并使其以最小的重构工作量快速响应重构需求．

NSGA-Ⅱ算法是解决此类多目标优化问题最常用的方法[7-9]．如图8所示，两种算法在200次迭代后，MOCS快速收敛并取得Pareto最优解，而NSGA-Ⅱ在300次迭代后完全收敛并取得Pareto最优解，从而证明MOCS比NSGA-Ⅱ收敛速度快、搜索效率高.

4 结 论

本文以模块化RMT原型为基础，提出了一种基于工序与RMT映射关系及MOCS 算法的RMT优选方法．并用一个案例对该方法进行验证与测试，结论如下．

(1)该方法综合考虑了设备级和系统级两个层级的重构过程对RMT优选结果的影响．实现了对RMS重构过程的综合量化评估，保证了方法的有 效性．

(2)基于MOCS算法，该方法综合全局搜索和局部搜索两种搜索方法，该案例能在200次迭代后求得Pareto最优解集，与NSGA-Ⅱ算法比较，不仅避免了陷入局部最优解，还提高了该方法的运行效率．

(3)该方法能针对零件族的生产，根据两个目标函数优选出用于集成低成本、高重构能力及响应能力RMS的RMT集合，对RMS设计具有重要意义．

本文仅通过重构指数评价RMS性能，未来的研究工作将进一步考虑RMS可扩展性及可集成性等其他性能指标对RMT优选结果的影响．

［1］ Bortolini M，Galizia F G，Mora C. Reconfigurable manufacturing systems：Literature review and research trend[J]. Journal of Manufacturing Systems，2018，49：93-106.

［2］ 王成恩. 制造系统的可重构性[J]. 计算机集成制造系统，2000，6(4)：1-5.

Wang Cheng’en. On the possibility of manufacturing system reconfiguration[J]. Computer Integrated Manufacturing Systems，2000，6(4)：1-5(in Chinese).

［3］ Koren Y. The rapid responsiveness of RMS[J]. International Journal of Production Research，2013，51(23/24)：6817-6827.

［4］ Montalto A，Graziosi S，Bordegoni M，et al. An approach to design reconfigurable manufacturing tools to manage product variability：The mass customization of eyewear[J]. Journal of Intelligent Manufacturing，2018，31：87-102.

［5］ Xu Z，Xi F，Liu L，et al. A method for design of modular reconfigurable machine tools[J]. Machines，2017，5(1)：1-16.

［6］ 蔡宗琰，杨旭东，严新民. 可重构模块化机床的集成设计[J]. 机床与液压，2002(5)：132-136.

Cai Zongyan，Yang Xudong，Yan Xinmin. Integrated design for reconfigurable modular machine tools[J]. Machine Tool & Hydraulics，2002(5)：132-136(in Chinese).

［7］ Bensmaine A，Dahane M，Benyoucef L. A non-dominated sorting genetic algorithm based approach for optimal machines selection in reconfigurable manufacturing environment[J]. Computers and Industrial Engineering，2013，66(3)：519-524.

［8］ Dahane M，Benyoucef L. An adapted NSGA-Ⅱ algorithm for a reconfigurable manufacturing system(RMS) design under machines reliability constraints[J]. Operations Research/Computer Science Interfaces Series，2016，60：109-130.

［9］ Benderbal H H，Dahane M，Benyoucef L. Flexibility-based multi-objective approach for machines selection in reconfigurable manufacturing system(RMS)design under unavailability constraints[J]. International Journal of Production Research，2017，55(20)：6033-3051.

［10］ Benderbal H H，Dahane M，Benyoucef L. Modularity assessment in reconfigurable manufacturing system (RMS)design：An archived multi-objective simulated annealing-based approach[J]. International Journal of Advanced Manufacturing Technology，2018，94(14)：729-749.

［11］ Huang S，Yan Y. Design of delayed reconfigurable manufacturing system based on part family grouping and machine selection[J]. International Journal of Production Research，2019，58(4)：4471-4488.

［12］ Ming Z，Zeng C，Wang G，et al. Ontology-based module selection in the design of reconfigurable machine tools[J]. Journal of Intelligent Manufacturing，2020，31：301-317.

［13］ Huang S，Xu Z，Wang G，et al. Reconfigurable machine tools design for multi-part families[J]. International Journal of Advanced Manufacturing Technology，2019，105(14)：813-829.

［14］ 李一全，姜 倩，许金凯，等. 可重构机床新型接口设计[J]. 组合机床与自动化加工技术，2015(12)：81-84，89.

Li Yiquan，Jiang Qian，Xu Jinkai，et al. Interface design of reconfigurable machine tool[J]. Modular Machine Tool & Automatic Manufacturing Technique，2015(12)：81-84，89(in Chinese).

［15］ Yang X S，Deb S. Multi-objective cuckoo search for design optimization[J]. Computers and Operations Research，2013，40(6)：1616-1624.

［16］ 陈 雷，张红梅，张向利. 自适应动态邻域布谷鸟混合算法求解TSP问题[J]. 计算机工程与应用，2018，54(23)：42-50.

Chen Lei，Zhang Hongmei，Zhang Xiangli. Adaptive dynamic neighborhood hybrid cuckoo search algorithm for solving traveling salesman problems[J]. Computer Engineering and Applications，2018，54(23)：42-50(in Chinese).

［17］ Yang X S，Deb S. Cuckoo search via levy flights[C]// World Congress on Nature and Biologically Inspired Computing. Coimbatore，India，2009：210-214.

［18］ Yang X S，Deb S. Cuckoo search：Recent advances and applications[J]. Neural Computing and Applications，2014，24(1)：169-174.

Multi-Objective Optimization Selection Method for the Reconfigurable Machine Tool

Wang Taiyong1, 2，Sun Xiran1，Tian Songling3, 4，Zhang Lei5，Ma Mingzhu1

(1. School of Mechanical Engineering，Tianjin University，Tianjin 300350，China；2. Tianjin University Ren’ai College，Tianjin 301636，China；3. School of Control and Mechanical Engineering，Tianjin Chengjian University，Tianjin 300384，China；4. Tianjin TSNC Science and Technology Co.，Ltd.，Tianjin 300392，China；5. School of Mechanical Engineering，Tianjin University of Commerce，Tianjin 300134，China)

The modular reconfigurable machine tool(RMT) enables the reconfigurable manufacturing system(RMS) to produce part families efficiently，which has a significant effect on the reconfigurability and responsiveness of the RMS. To design an RMS with a low cost and high reconfigurable capability，a multi-objective optimization method for the RMT based on the cuckoo search algorithm is proposed. First，the mapping relationship between operations and RMTs is established by machining direction. Second，considering that reconfiguration is required in a manufacturing system to produce the different parts in a part family，the RMT is identified to clearly describe the change in the RMT in the reconfiguration process of the RMS. Third，the reconfiguration cost and reconfiguration index in the reconfiguration process are quantified from the machine level and system level，respectively. Based on this analysis，two objective functions are proposed：minimizing the design cost of the RMS and maximizing the reconfiguration index. Finally，the effectiveness of the method is verified using an engineering example. The case results show that the lowest design cost is 316.7，while the best reconfiguration index is 27.4. In addition，compared with NSGA-Ⅱ，a commonly used multi-objective optimization algorithm，the multi-objective cuckoo search(MOCS) can quickly converge and obtain the global Pareto optimal solution after 200 iterations，and it is proved that the proposed method can quickly screen out the RMT selection solution with a more economical and higher reconfiguration index. The proposed multi-objective optimization method can provide guidance for subsequent research and production practice.

reconfigurable machine tool；reconfigurable manufacturing system；machine selection；multi-objectivecuckoo search(MOCS) algorithm

TH164

A

0493-2137(2021)09-0881-09

10.11784/tdxbz202006021

2020-06-08；

2020-11-09.

王太勇（1962—  ），男，博士，教授，tywang@tju.edu.cn.

孙熙冉，sunxiran@tju.edu.cn.

国家自然科学基金资助项目(51975402).

Supported by the National Natural Science Foundation of China(No. 51975402).

(责任编辑：王晓燕)