运用数学思维巧解基因频率计算题
2021-05-31安徽
安徽
基因频率计算一直是高中教学的重难点,这部分习题往往在生物学原理的外壳下有着数学思维的内核,所以运用数学思维、借助数学工具解决此类题目往往可举重若轻,事半功倍。利用数学原理揭示生物学规律,可以使得解题思路简单清晰、直观形象,学生便于掌握。本文就基因频率计算的典型例题介绍三种常见的运用数学思维的解题思路。
1.函数图形思维
【例1】隐性基因(a)可导致人患一种遗传病,使得基因型为aa 的儿童在10 岁前全部死亡,而基因型为Aa和AA的个体都表现正常。在一个隔离的群体的第一代(Ⅰ)中,基因a 在成人中的频率为0.01,如果没有新的突变发生,在下一代(Ⅱ)的成人中基因a 的频率以及下一代的新生儿中杂合子(Aa)的频率的变化趋势分别是 ( )
A.下降、上升 B.上升、下降
C.下降、下降 D.上升、上升
【答案】C
【错因分析】学生对于a 的基因频率变化趋势并不难推断,按照题干信息(基因型为aa 的儿童在10 岁前全部死亡),其应该随着基因型为aa 的个体数量减少而下降。而本题的难点是对Aa 基因型频率的变化趋势的判断。a 的基因频率一直在下降,A 的基因频率一直在上升,Aa 的基因型频率很难判断,学生思考至此,往往很难继续分析,无从下手,造成误判。但解决此题的“金钥匙”是分析Aa的基因型频率随着A 或a 的基因频率变化而如何变化,这像极了高中数学常见的曲线函数问题。按照高中学生此时的数学思维能力,没有哪一种方法比构建函数公式、绘制曲线图更能恰当地描述这一变化规律。这种思考模式对于高中生的学科交叉思维的形成和发展有极其重要的促进作用,表面上看只是解决了一道题,其实学生已经可以利用构建的数学模型解决生物学问题了。
【正解分析】构建Aa 的基因型频率的函数表达式,绘制相关的曲线图。
设P(Aa)=y,P(A)=x,则P(a)=1-x;
[注:P(Aa)、P(A)、P(a)分别表示Aa的基因型频率、A的基因频率、a的基因频率。]
按照“哈迪-温伯格平衡定律”,P(Aa)=2·P(A)·P(a)=2·x·(1 -x)=2x -2x2;
化简得:y=-2(x -1/2)2+1/2,
函数图像如图所示:

注意:此时P(A)的取值范围是0.99 ≤P(A)<1,即x ∈[0.99,1)。而通过函数曲线可以看到,当x ∈[0.99,1)时,y 值递减,即P(Aa)的变化趋势是下降。
所以,如果没有新的突变发生,在下一代(Ⅱ)的成人中基因a 的频率和下一代的新生儿中杂合子(Aa)的频率的变化趋势都是下降,应该选择C。
【反思】本题利用的数形结合思想是常见的数学解题技巧,高中生应当并不陌生,但在生物学习题的解题情境中使用对学生来说可能会感觉到十分新颖,有助于激发其学习兴趣。其实,生物习题的解题思维与图形走势的曲线分析联系密切,如恶劣条件下自由水和结合水的变化曲线;细胞分裂过程中染色体、染色单体和DNA 的变化曲线;种群“J”型增长曲线及λ 值变化曲线等,这些题型的模型都可以在数形结合的数学思维体系中构建,教师在新课教学中应予以重视,在复习课教学中可以专题形式强化学生相关能力的训练。
2.二项式展开的函数思维
【例2】在一个人类样本群体中AB 血型23 人,O 血型441 人,B 血型371 人,A 血型65 人。则IA、IB、i 各等位基因的基因频率分别为_________、_________、__________。
【答案】5% 25% 70%
【错因分析】遗传平衡定律在2 个等位基因的遗传题中的应用比较常见,学生练习较多,已经形成定式思维。而此题涉及复等位基因遗传,原有仅涉及2 个等位基因的遗传平衡定律公式无法满足解题要求,学生往往手足无措。那么如何应用遗传平衡定律公式呢?此题也可运用遗传平衡定律,不过由于涉及3 个等位基因,二项式公式需变形调整为三项式公式,像是对原有遗传平衡定律的升级,其实核心只是三项式展开的运算技巧。关键是要对展开式中的各项赋予生物学含义,即各项代表某基因的基因频率或某基因型的基因型频率。
【正解分析】人的ABO 血型系统决定于3 个等位基因IA、IB和i。设基因IA的基因频率为p,基因IB的基因频率为q,基因i 的基因频率为r,即且人群中p+q+r=1。根据基因的随机结合,用下列三项式展开式可求出子代的基因型及频率(如表1)。
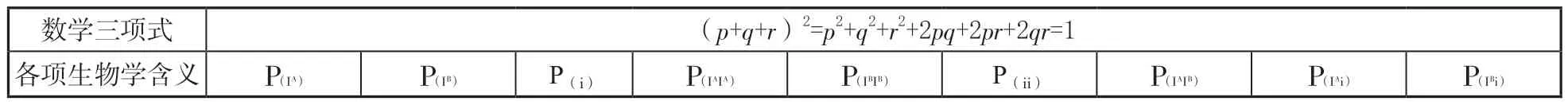
表1
A 血型(IAIA,IAi)的基因型频率为p2+2pr;B 血型(IBIB,IBi)的基因型频率为q2+2qr;O 血型(ii)的基因型频率为r2,AB 血型(IAIB)的基因型频率为2pq。可罗列出方程组,并解方程组。
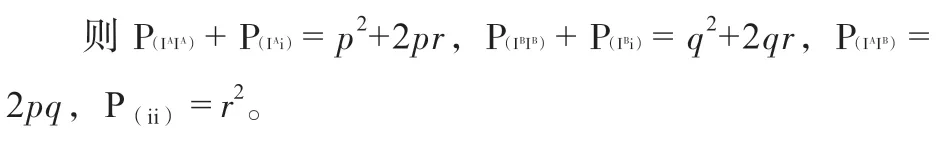
O 血型的基因型频率应为解答本题的突破口,P(ii)=r2=441÷(23+441+371+65)=0.49,则r=0.7。
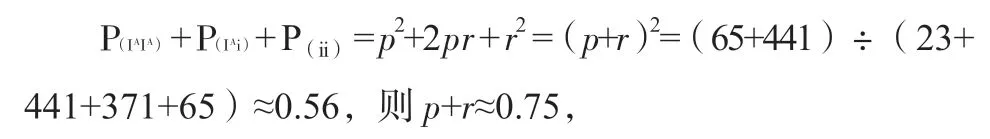
解得p=0.05,q=0.25。
所以,IA、IB、i 各等位基因的基因频率分别为5%、25%、70%。
【反思】由计算基因频率的遗传平衡定律二项式展开推导到三项式展开,并且赋予各项生物学含义,体现的是学生解题技能的即时生成性,这是一种学以致用且能举一反三的能力。在教学中,教师若想提升学生的其他类型习题解题能力,则这种公式化的变形训练也是必不可少的。教学中,理论学习立足于公式,但解决实际情境的问题不能拘泥于公式,如对分离定律、自由组合定律的相关性状分离比的变形分析。
3.“棋盘子”法解题思维
【例3】果蝇种群中,XB的基因频率为80%,Xb的基因频率为20%,雌雄果蝇数目相等,理论上XbXb、XbY的基因型频率分别是___________、____________。
【答案】2% 10%
【错因分析】这种题目往往都构建在理想状态的情境下,即题干中所明示的雌雄果蝇数目相等,但还有暗示,即XB和Xb的基因频率在果蝇种群的雌性群体和雄性群体中的分布是一致的,这是解决这一类题目的“潜规则”。学生往往易等同于常染色体的基因频率或基因型频率计算方法,从而出现错误。
【正解分析】雌雄果蝇数目相等,即在两性果蝇群体产生的雌雄配子中,XB和Xb在雌性配子和含有X 染色体雄性配子中的基因频率是一致的,而含有X 染色体雄性配子和含有Y 染色体雄性配子各占一半,所以雌雄配子的基因型和比例具有差异,十分容易出现混淆。若利用“棋盘子”构建雌雄配子类型及比例,可直观反映出后代受精卵基因型及比例,如表2 所示。
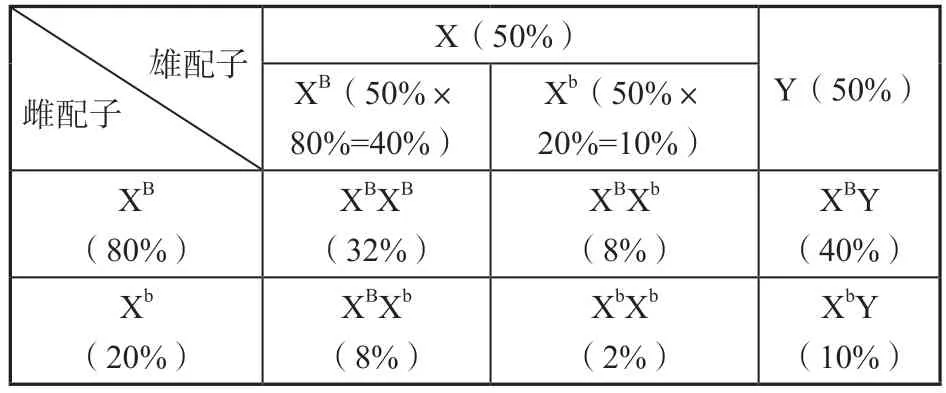
表2
由上表可以看出,XbXb、XbY 的基因型频率分别是2%、10%。
运用“棋盘子”法最为关键的一步是要准确求出雌雄配子中相关基因各自所占的比例,也就是构建“棋盘子”的边长,在此基础之上,边长所辖的“棋盘子”面积(即雌雄配子自由组合)所涉及的各种子代基因型和表现型比例计算便水到渠成。
【反思】通过亲代的基因型推导其配子基因型及比例,继而推导子代的相关基因型频率,是遗传题常见的解题思路,但若雌雄个体出现多种配子类型甚至是异常配子类型,在推导子代基因型及比例的过程中,容易出现遗漏或错配。使用“棋盘子”法,雌雄配子类型及比例清晰明了,各种组合对号入座,与使用教材中的连线法相比,学生的正确率更高。
4.总结
由以上三个实例可以看出在高中生物学的日常教学中,教师引导学生进行相关的数学思维能力训练是十分必要的。其实生物学很多理论的得出往往依赖于数学模型的构建分析,来源于对数学工具的使用。如通过相对表面积公式了解细胞不能无限长大的原因,通过大量数据的统计学分析得到基因分离定律、自由组合定律,通过函数公式和曲线模型描述种群增长规律。利用数学思维,使用数学工具更能客观、形象地揭示生物学规律,在揭示生物学规律的道路上,众多生物学家对于数学的痴迷甚至使得生物学衍生出了一门和数学相关的分支学科——生物数学。所以,在生物学教学中适时、适度穿插数学思维及方法,不仅有助于学生解决实际的生物学问题,还能使得学生重温数学在生物学理论的诞生过程中体现重大价值的科学史实,从而提高中学生的学科核心素养。
